Teori :: Diofantiska ekvationer v1.2

Teori :: Diofantiska ekvationer
1
v1.2
Definitioner och inledande exempel
Låt oss börja med att göra klart för vad vi menar med en diofantisk ekvation:
Definition 1.1.
S:def+ex
Betrakta ekvationen
D:diofantiskEkv
ax + by = c,
där a, b och c är heltal. Om x och y tillåts vara godtyckliga reella tal så bildar lösningarna en
rät linje i planet. När man bara är intresserade av heltalslösningar , dvs x, y ∈ Z så kallar man
ekvationen för en diofantisk1 ekvation.
4
3
2
1
-4
2
-2
4x+6y=3
-1
4x+6y=4
-2
2x+3y=0
-3
4
3x+3y=1
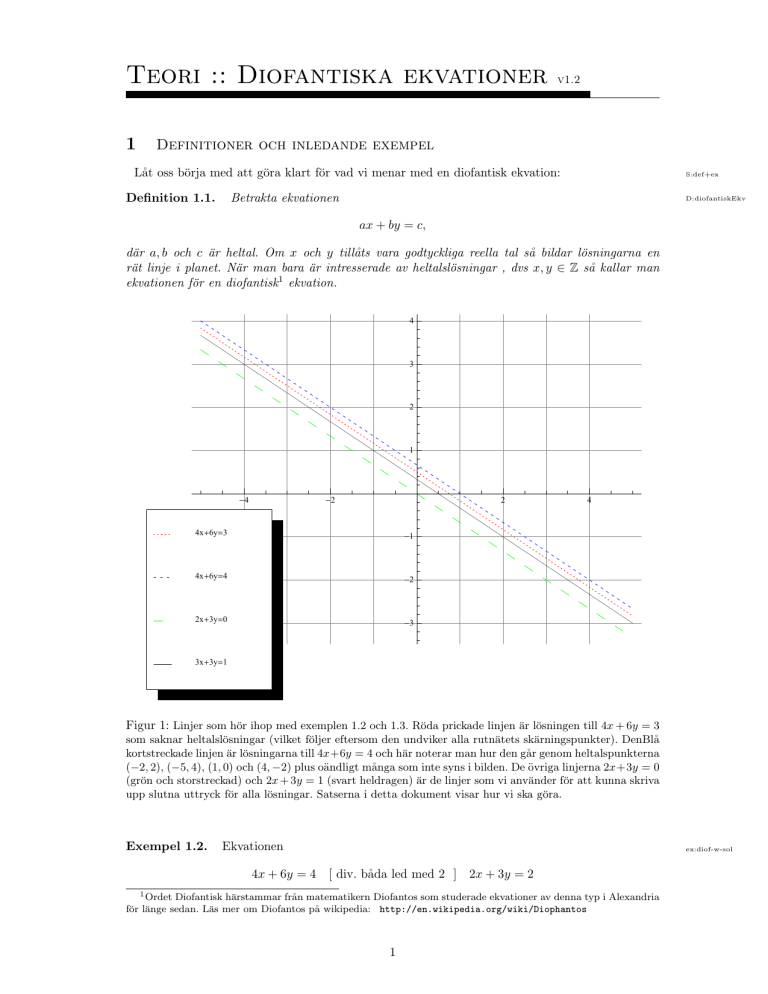
Figur 1: Linjer som hör ihop med exemplen 1.2 och 1.3. Röda prickade linjen är lösningen till 4x + 6y = 3
som saknar heltalslösningar (vilket följer eftersom den undviker alla rutnätets skärningspunkter). DenBlå
kortstreckade linjen är lösningarna till 4x+6y = 4 och här noterar man hur den går genom heltalspunkterna
(−2, 2), (−5, 4), (1, 0) och (4, −2) plus oändligt många som inte syns i bilden. De övriga linjerna 2x+3y = 0
(grön och storstreckad) och 2x + 3y = 1 (svart heldragen) är de linjer som vi använder för att kunna skriva
upp slutna uttryck för alla lösningar. Satserna i detta dokument visar hur vi ska göra.
Exempel 1.2.
Ekvationen
4x + 6y = 4
ex:diof-w-sol
[ div. båda led med 2 ]
2x + 3y = 2
1 Ordet Diofantisk härstammar från matematikern Diofantos som studerade ekvationer av denna typ i Alexandria
för länge sedan. Läs mer om Diofantos på wikipedia: http://en.wikipedia.org/wiki/Diophantos
1
har reella lösningar i form av en linje (blå kortstreckad linje) i figur 1. Heltalslösningarna får man
i de punkter där linjen skär rutsystemet i Figuren. Det är inte svårt att se att vi får en oändlig
mängd sådana lösningspunkter eftersom lutningen av linjen har en sådan egenskap.
Exempel 1.3.
Ekvationen
ex:diof-noSol
4x + 6y = 3
har reella lösningarna beskrivna av den röda prickad linjen i figuren ovan. Notera att denna linje
inte går genom rutnätets skärningspunkter och saknar därför heltalslösningar. Ett annat och mer
precist sätt att visa detta är: om x och y vore heltal så kan man säga att 2 delar vänster led.
Likheten skulle då kräva att 2 också måste dela 3 vilket alltså inte är sant. Eftersom en eventuell
heltalslösning leder till en omöjlighet så kan det därför inte finnas några heltalsvärden som löser
vår ekvation.
2
Lösbarhet för Diofantiska ekvationer
S:solvability
Givet en Diofantisk ekvation
ax + by = c
så har vi i de ovanstående exemplen sett att lösbarheten beror på de ingående heltalen a, b och
c. Om ekvationen ska ha heltalslösningar så ställer det krav på ekvaitionens parametrar. Om t.ex
ett tal delar både a och b så betyder det att för x och y heltal att detta tal delar vänster led.
Likheten ger då att detta tal också måste dela c som utgör höger led. Detta är det så kallade
lösbarhetskravet:
Proposition 2.1.
Om ekvationen
P:solvecondition
ax + by = c
har heltalslösningar så måste SGD(a, b)|c.
Bevis. Om x, y båda är heltal som löser ekvationen så gäller att SGD(a, b) måste dela vänster led
eftersom båda termerna har a respektive b som faktor varför vänster led kan faktoriseras som
ax + by = M · m,
där M = SGD(a, b) och m ∈ Z. Om nu ekvationen är uppfylld så måste c också ha M som faktor
eftersom vi annars skulle få motsägelsen att vänster led är delbar men inte höger led.
Proposition 2.2.
Varje lösbar Diofantisk ekvation kan skrivas som
ax + by = c,
SGD(a, b) = 1
Bevis. Lösbarhetskravet ger för en godycklig ekvation a0 x + b0 y = c0 att båda led är delbara med
SGD(a, b) och då kan man dividera båda led med detta tal och få en ekvation ax + by = c där
a0 = a · SGD(a, b), b0 = b · SGD(a, b) och c0 = c · SGD(a, b) som vi alltså får om vi dividerar båda
led med SGD(a, b). Eftersom vi dividerat bort den största gemensamma faktorn så följer det att
SGD(a, b) = 1
2
P:genericDio
3
Huvudsatsen och dess hjälpsatser
S:huvudsats
Vi ska nu redogöra för hur man löser en diofantisk ekvation. Vi ska visa följande huvudsats som
exakt talar om hur vi ställer upp lösningarna.
Theorem 3.1.
Låt a, b ∈ Z och SGD(a, b) = 1. Då har den diofantiska ekvationen
T:Sol2Diofant
E:Diofant
ax + by = c
(1)
lösningarna
x
= −bn + cx0
y
= an + cy0 ,
där nZ och där (x0 , y0 ) är lösning till den diofantiska ekvationen
ax + by = 1
Lösningen kan också uttryckas på vektorform som
x
−b
x0
=
n+c
,
y
a
y0
och här är
x
y
=
−b
a
n
heltalslösningarna till den homogena ekvationen
ax + by = 0
och vektorn (−b, a) är skillnadsvektorn mellan två på varandra följande heltalslösningarn.
Beviset för satsen beror av ett antal hjälpsatser2
Lemma 3.2.
Heltalslösningarna till
L:homogena
ax + by = 0
kan skrivas på formen
xh
yh
=
−b
a
n
Bevis. (av lemma 3.2) Vi har att ax + by = 0 ger oss att x = − ab y. Om vi sätter y = t så kan vi
alltså skriva lösningarna på vektorform som
−b −b
x
a
t = [ sätt t = as ] =
s,
=
a
y
1
som ger oss heltalslösningar om s = n ∈ Z. Eftersom sgd(a, b) = 1 så är vektorn (−b, a) den
kortaste vektor som kan bildas mellan två heltalslösningar.
Lemma 3.3.
Om (x0 , y0 ) löser ekvationen ax + by = 1 så löser c(x0 , y0 ) ekvationen ax + by = c.
Bevis. (Av lemma 3.3)
Beviset är busenkelt: Följande räkningar
a(cx0 ) + b(cy0 ) = c (ax0 + by0 ) = c
|
{z
}
=1
ger oss direkt lemmats utsaga.
2 En
hjälpsats kallas i matematiken ofta för ett Lemma
3
L:partikular
Lemma 3.4. Givet en prtikulär lösning (xp , yp ) till ax + by = c så får man övriga lösningar
genom genom att addera de homogena lösningarna dvs
x
xh
xp
=
n+
y
yh
yp
L:superposition
Bevis. Vi är klara om vi kan visa att två olika lösningar till (1) skiljer sig åt med en lösning
till motsvarande homogena ekvation. Eller, uttryckt på annat sätt: Om (xp , yp ) och (x1 , y1 ) är
två partikulära lösningar till (1) så behöver vi visa att det finns ett heltal n så att (x1 , y1 ) =
(−b, a)n + (xp , yp ). Detta ger direkt att vi behöver visa att (x1 , y1 ) − (xp , yp ) = (x1 − xp , y1 − yp )
är en lösning till den homogena ekvationen, vilket vi gör så här. Vi sätter in denna vektor i vänster
led av den homogena ekvationen. Vi behöver då visa att detta blir noll:
a(x1 − xp ) + b(y1 − yp ) = ax1 + by1 − (axp + byp ) = c − c = 0
| {z } |
{z
}
=c
=c
Detta visar att skillnaden mellan två lösningar till en diofantisk ekvation är en lösning till motsvarande homogena ekvation.
Lemma 3.5. En partikulärlösning till ax + by = 1 får man fram genom att använda Euklides
algoritm baklänges.
L:partikEuklid
Bevis. (Lemma 3.5) Med Euklides algoritm så kan vi beräkna största gemensamma delare till a
och b. Eftersom SGD(a, b) = 1 så ger Genom att gå baklänges i Euklidesschemat så kjan vi skriva
SGD(a, b), dvs 1 sin en linjärkombination av a och b: dvs ak + bm = 1 som alltså ger en lösning
till ax + by = 1.
Låt oss exemplifiera metoden i Lemma 3.5:
Exempel 3.6. Vi söker en partikulärlösning (x0 , y0 ) till 35x + 33y = 1:
Med a = 35 och b = 33. Euklides algoritm ger oss
ex:euklid
35 = 1 · 33 + 2
33 = 16 · 2 + 1
Här ser vi alltså att SGD(35, 33) = 1.
Med början av den sista ekvationen så har vi att
1 = 33 − 16 · 2 =
[ 2 uttrycks mha den första ekvationen ] =
= 33 − 16 · (35 − 1 · 33) =
|
{z
}
=2
= 33 − 16 · 35 − 16 · 33 = (−16) ·35 + (−15) ·33
| {z }
| {z }
=x0
4
=y0
Bevis för huvudsats
S:theProof
Vi är nu redo för att visa huvudresultatet Theorem 3.1. Tack vare alla hjälpsatser (lemmorna) så
blir beviset av satsen väldigt rättframt:
4
Bevis. (Av Theorem 3.1) Vi börjar med att beräkna en partikulärlösning (x0 , y0 ) till ax + by = 1
genom att använda Euklides algoritm som vi visade i Lemma 3.5. Sedan visar Lemma 3.3 att
c(x0 , y0 ) är en partikulärlösning till (1).
Från Lemmorna 3.4 och 3.2 har vi att alla lösningar till (1) kan skrivas på formen
x
−b
x0
=
n+c
,
y
a
y0
vilket slutför beviset för vår sats.
5
Exempel
S:exempel
Exempel 5.1. Vi använder nu satsen för att beräkna lösningarna till exempel 1.2.
Först beräknar vi en lösning till 2x + 3y = 1. Denna ekvation är så enkel att vi snabbt kan hitta
en heltalslösning utan att använda Euklides algoritm:
Om vi tar t.ex. x0 = 2 och y0 = −1 så får vi tydligen en lösning. Detta ger nu att 2(2, −1) = (4, −2)
är en lösning till 2x + 3y = 2.
Vi bestämmer nu lösningarna till den homogena ekvationen 2x + 3y = 0. Om vi löser ut x som
funktion av y och betecknar y med parametern t så får vi på vektorform
3 −3
xh
−2
s
=
t = [ sätt t = 2s ] =
2
yh
1
ex:example
Genom att kombinera lösningen (m.h.a. Lemma 3.4 )till den homogena ekvationen med den partikulära lösningen så får vi slutligen den allmänna lösningen till vårt problem:
x
−3
4
=
s+
, s∈Z
y
2
−2
dvs x = −3s + 4 och y = 2s − 2.
Exempel 5.2.
Beräkna alla heltalslösningar till ekvationen
ex:normalisera
70x + 18y = 22.
Vi börjar med att notera ekvationen inte är på formen given i sats 3.1 så vi behöver börja med att
dividera båda led med SGD(70, 18) = 2. (Notera att om inte höger led också är delbar med denna
gemensamma delare så har inte ekvationen någon heltalslösning. See nästa exempel för en sådan
situation) Vi får då den diofantiska ekvationen
35x + 9y = 11,
där vi har att
SGD(35, 9) = 1
Genom att gå baklänges mha Euklides algoritm får vi att 1 = −1 · 35 + 4 · 9, vilket ger att x0 = −1
och y0 = 4 är en partikulärlösning till 35x + 9y = 1. Det följer då från Lemma 3.3 att xp = −11
och yp = 44 är en partikulärlösning till 35x + 9y = 11.
Lemma 3.2 ger oss nu den homogena lösningen xh = −9n, yh = 35n och då kan vi skriva upp
lösningen till vår diofantiska ekvation
x = −9n − 11,
Exempel 5.3.
y = 35n + 44,
n ∈ Z.
(2)
Beräkna den diofantiska ekvationen
52x + 39y = 11.
Vi noterar att om x och y är heltal så är 13 en delare till vänster led. Men eftersom höger led inte
är delbar med 13 så tillåter inte ekvationen att x och y är heltal, eftersom vi i så fall skulle få en
omöjlighet. Vår ekvation saknar alltså lösningar.
5
E:exampleSol
ex:noSols
6
Övningsuppgifter
S:uppgifter
Övning 1.
Verifiera att lösningarna (2) verkligen är lösningar till 35x + 9y = 11 för alla n ∈ Z.
ovn:verifiera
Övning 2.
Beräkna alla heltalslösningar till ekvationen
ovn:noSolution
63x + 27y = 24
Övning 3.
Lös den diofantiska ekvationen 45x + 84y = 33
6
ovn:a
7
Lösningar till uppgifterna
S:solutions
Lösning till uppgift 1
För att verifiera att (2) löser 35x + 9y = 11 så måste vi sätta in dem i ekvationen och visa att
vänster led blir lika med höger led. Vi får att vänster led (VL) blir:
V L = 35(−9n − 11) + 9(35n + 44) = −9 · 35n − 35 · 11 + 9 · 35n + 9 · |{z}
44 =
=4·11
= −35 · 11 + |{z}
36 ·11 = (36 − 35) · 11 = 11
=9·4
Eftersom höger led är just 11 så har vi alltså visatt att (2) verkligen är lösningarna till 35x+9y = 11
Lösning till uppgift 2
I denna uppgift så noterar man att 63 och 27 båda är delbara med 9. För att ekvationen ska ha
heltalslösningar så krävs det att även högerledet ska vara delbart med 9. Men höger led är bara
bara delbar med 3 och multiplar av 2 vilket betyder att denna ekvation saknar heltalslösningar.
Detta är också synligt om vi plottar linjen, vilket kan ses i figur 2
4
3
2
1
-4
2
-2
4
-1
-2
-3
Figur 2: Bild till uppgift 2. Om ekvationen har heltalspunkter så måste linjen gå genom rutnätets
skärningspunkter (som ju betyder att både x och y är heltal.
Lösning till uppgift 3
I ekvationen 45x + 84y = 33 så är siffrorna i både vänster och höger led delbara med 3 och gör vi
det så får vi ekvationen
15x + 28y = 11
Vi börjar med att beräkna en lösning till 15x + 28y = 1, vilket vi gör med euklides algoritm som
ger oss
28 = 1 · 15 + 13
15 = 1 · 13 + 2
13 = 6 · 2 + 1
Som ger att
1 = 13 − 6 · 2 = 13 − 6(15 − 13) = 13 − 6 · 15 + 6 · 13 =
= 7 · 13 − 6 · 15 = 7 · (28 − 15) + (−6) · 15 = 7 · 28 − 13 · 15 =
= 15 · (−13) + 28 · 7
7
vilket alltså ger oss lösningen (−13, 7) till 15x+28y = 1 och därför får vi att 11(−13, 7) = (−143, 77)
är en partikulär lösning till vår ekvation. Lösningen kan nu ställas upp mha av sats 3.1:
x = −28n − 143
y = 15n + 77
För säkerhets skull kan man göra en kontroll att detta verkligen är en lösning genom att sätta in
dessa värden i vår ekvation. Vi får då att vänster led blir:
15x + 28y = 15(−28n − 143) + 28(15n + 77) =
= −15 · 28n − 15 · 143 + 28 · 15n + 28 · 77 =
= 2156 − 2145 = 11
Eftersom höger led också är 11 kan vi vara trygga i att vår lösning verkligen är den rätta!
8

Teori :: Diofantiska ekvationer v1.2

Related documents

Products

Support

Teori :: Diofantiska ekvationer v1.2

Related documents

Add this document to collection(s)

Add this document to saved

Suggest us how to improve StudyLib