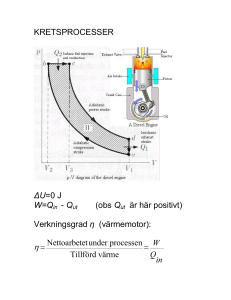
Instuderingsfrågor Energilagringsteknik 7,5 hp, vt 2012
Termodynamisk optimering av energilager (viss anknytning till kap 6)
1. Rangordna nedanstående lagringsprinciper i stigande exergieffektivitet samt motivera ordningen.
Skiktad ackumulatortank, Blandad ackumulatortank, Tre seriekopplade blandade tankar.
T − TO
⋅Q
T
Härled från detta samband exergiinnehållet hos en varm kropp med temperaturen T, massan m och
specifika värmekapaciteten cp.
2. Exergin för en värmekälla vid temperaturen T ges av: X =
3. Förklara varför exergiverkningsgraden är så mycket bättre när man använder sig av en skiktad
ackumulatortank jämfört med en blandad tank. (uppkopplingar som vid föreläsningen)
4. Den dimensionslösa tiden θ är ett mått på både tid, flödeshastighet och lagrets storlek. Förklara de
olika tolkningarna.
5. Betrakta ett enkelt sensibelt energilager som laddas av en gasström enligt figur nedan. Var har vi
energiförlusterna respektive exergiförlusterna.
Tin
m& c P
Tg ( x, t )
T (t )
MC
Tout (t )
TO
Lösningsförslag
1. Rangordna nedanstående lagringsprinciper i stigande exergieffektivitet samt motivera ordningen.
Skiktad ackumulatortank, Blandad ackumulatortank, Tre seriekopplade blandade tankar.
Ordningen ska vara:
Blandad ackumulatortank, Tre seriekopplade blandade tankar, Skiktad ackumulatortank.
Motivering:
Den skiktade ackumulatortanken lagrar nästan all energi vid hög temperatur, vilket ger mer exergi än
de övriga. Den blandade tanken är sämst för där lagras energin vid så låg temperatur som möjligt,
vilket ger liten exergi.
T − TO
⋅Q
T
Härled från detta samband exergiinnehållet hos en varm kropp med temperaturen T, massan m och
specifika värmekapaciteten cp.
2. Exergin för en värmekälla vid temperaturen T ges av: X =
Om vi har en varm kropp får vi fram exergin genom att integrera X =
T − TO
⋅ Q från
T
omgivningstemperaturen TO till den aktuella temperaturen T:
T
T
T
T
T
T − TO
dT
TO
TO
X=∫
dQ = ∫ 1 − dQ = ∫ 1 − mc P dT = mc P ∫ dT − TO ∫
T
T
T
T
T
TO
TO
TO
TO
O
där dQ är den värmemängd som upptas när temperaturen ändras med dT.
Vilket innebär att exergin för en massa där cP är konstant (oberoende av T) ges av
T
X = mc P T − TO − TO ln
TO
3. Förklara varför exergiverkningsgraden är så mycket bättre när man använder sig av en skiktad
ackumulatortank jämfört med en blandad tank. (uppkopplingar som vid föreläsningen)
Vid laddning av en blandad tank har vi temperaturskillnader mellan lagret och det medium som
används för att ladda tanken. Den blandade tanken kan inte heller ta rätt på all energi och exergi från
det medium som används för att ladda den eftersom när tanken är halvladdad kan den inte kyla till en
lägre temperatur än tankens temperatur.
En skiktad tank är idealt reversibel, dvs med en ideal värmeväxlare är exergiverkningsgraden 100%.
4. Den dimensionslösa tiden θ är ett mått på både tid, flödeshastighet och lagrets storlek. Förklara de
olika tolkningarna.
θ är en dimensionslös tid enligt:
m& c P t Termiska massa för genomströmmad gas
=
MC
Termiska massa hos lagret
Dvs. θ är proportionell mot både tiden (t) och flödeshastigheten ( m& ), samt omvänt proportionell mot
lagrets storlek (MC).
θ=
5. Betrakta ett enkelt sensibelt energilager som laddas av en gasström enligt figur nedan. Var har vi
energiförlusterna respektive exergiförlusterna.
Tin
m& c P
Tg ( x, t )
T (t )
Tout (t )
TO
MC
Energiförluster:
• Utloppstemperaturen Tout är högre än omgivningstemperaturen TO
• Förluster genom lagrets isolering.
Exergiförluster:
• Utloppstemperaturen Tout är högre än omgivningstemperaturen TO
• Förluster genom lagrets isolering.
• Temperaturskillnaden mellan lagret och gasen ger en exergiförlust.
