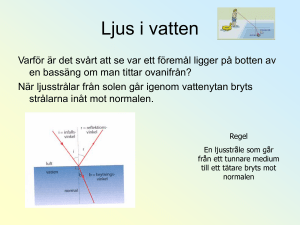
Ljusbrytning - WordPress.com
advertisement

Optik Stråloptik Ljus uppvisar många märkliga egenskaper och det behövs olika typer av modeller för att beskriva ljus i olika situationer. • Ljus beskrivs som vågor som utbreder sig • Ljus beskrivs som ett knippe partiklar (fotoner) som utbreder sig • Ljus beskrivs som strålar som utbreder sig längs räta linjer. Detta kallas stråloptik, eller geometrisk optik. Exempel • Färgringar som uppstår då en tunn oljefilm flyter på vatten • Svartkroppsstrålning • Laser • Linssystem som kamera, mikroskop, etc. Det elektromagnetiska spektrumet Stråloptik Elektromagnetiska vågor delas in i olika områden beroende på dess våglängd: Frekvensområde • Radiovågor • Mikrovågor • Infraröd strålning • Synligt ljus • Ultraviolett strålning • Röntgenstrålning • Gammastrålning Skapas vid: • Elektriska svängningskretsar • Klystroner (elektronrör) • Molekylvibrationer • Elektronexcitationer • Elektrisk urladdning • Inbromsning av snabba elektroner • Radioaktivt sönderfall Stråloptik Vågfronter och ljusstrålar I många sammanhang är det praktiskt att representera ljusvågor med ljusstrålar. Vågfronter Ljuskälla Ljusstrålar Vågfronter Ljusstrålar Reflektion Då ögat tar emot en ljusstråle så tolkar hjärnan det som om strålen kommer från ett objekt längs en rät linje. Stråloptik Reflektion Normalriktning Inkommande ljusstråle Reflekterad ljusstråle i r Stråloptik Riktningen av en ljusstråle som faller in emot, eller utgår från en yta definieras av vinkeln mellan ljusstrålen och normalriktningen Normalriktningen till en yta är vinkelrät mot ytan. Vid reflektion så är reflektionsvinkeln lika stor som infallsvinkeln i = r Stråloptik Reflektion Då ögat tar emot en ljusstråle så tolkar hjärnan det som om strålen kommer från ett objekt längs en rät linje. Spegel reflektion Ljusstrålar som når ögat kommer från ett objekt Diffus reflektion Ljusstrålar som når ögat kommer från många olika objekt Yta ojämn normalrikningen varierar reflektionsvinkel = infallsvinkel reflektionsvinkel = infallsvinkel Plan spegel Spegelbilden från en plan spegel har följande egenskaper: • Bilden har samma storlek som objektet. • Bilden är lokaliserad lika långt bakom spegeln som objektet är framför. • Höger och vänster är skiftade i bilden. • Bilden är ej upp och nedvänd. • Bilden är virtuell (det går inga ljusstrålar från den) Stråloptik Stråloptik Krökta speglar Vanligaste typen av krökta speglar är sfäriska speglar Det finns två typer av sfäriska speglar: Ljusstråle Huvudaxel, eller symmetriaxel Ljusstråle Huvudaxel, eller symmetriaxel Konkav spegel Konvex spegel Stråloptik Sfäriska speglar Bildpunkt Ljusstrålar som utgår från ett objekt, och som ligger nära huvudaxeln bryts till en gemensam punkt. Denna punkt kallas bildpunkt. När ljusstrålarna når ögat tycks de komma från bildpunkten och hjärnan tolkar det som om objektet fanns i bildpunkten. Eftersom ljusstrålarna verkligen kommer från bildpunkten kallas bilden för reell. Stråloptik Sfäriska speglar • Ljusstrålar som är parallella med huvudaxeln, och som träffar spegeln nära huvudaxeln bryts mot en gemensam punkt. • Denna punkt kallas brännpunkt och betecknas F. • Avståndet mellan spegel och brännpunkt, f, kallas brännvidd, eller fokallängd. • För en konkav spegel gäller att f = R/2 Brännpunkt R C F f Stråloptik Sfäriska speglar Parallella strålar som träffar spegeln långt från huvudaxeln bryts ej mot brännpunkten. Detta ger upphov till en suddig bild och kallas för sfärisk aberration. Felet kan minimeras genom att låta spegelns höjd vara liten i jämförelse med krökningsradien. Det finns krökta speglar med parabolisk form för vilka alla strålar parallella med huvudaxeln bryts mot brännpunkten. C F Stråloptik Konkav spegel - bildkonstruktion C F För att bestämma bildens läge utnyttjas tre olika strålar. Stråle 1: Parallell med huvudaxel, reflekteras och går igenom brännpunkten. Stråle 2: Går från objekt genom brännpunkten, reflekterad stråle parallell med huvudaxel. Stråle 3: Går igenom spegelns (cirkelns) medelpunkt, reflekteras tillbaka i samma riktning. Stråloptik Konkav spegel - bildkonstruktion • Objektet utanför C: Bild som är reell, inverterad och mindre än objektet. • Objektet mellan F och C: Bild som är reell, inverterad och större än objektet. • Objektet innanför F: Divergerande strålar, men betraktat mha ett öga Bild som är virtuell, rättvänd C och större än objektet. F C F C F Stråloptik Spegelekvationen Bildens läge kan bestämmas med spegelekvationen do Spegelekvationen 1/do + 1/di = 1/f Linjär förstoring för en sfärisk spegel m = [bildhöjd / objekthöjd ] = = hi / ho = - di / do ho C hi F f di • f = brännvidd • do = avstånd till objekt • di = avstånd till bild • do = objekthöjd • di = bildhöjd • m = förstoring Stråloptik Konvex spegel - bildkonstruktion Strålkonstruktion för en konvex spegel sker på motsvarande sätt som för en konkav spegel F Exempel: Var hamnar bilden, och hur stor blir den om f = -10 cm, do = 15 cm och ho = 5 cm? Lösning: 1/di = 1/f - 1/do = - 1/10 - 1/15 = - 5/30 = -1/6 di = - 6 cm hi = m ·ho = -( di/do) ·ho = - ( -6/15 ) ·5 = 2 cm C Stråloptik Ljusbrytning När ljus passerar från ett medium till ett annat så ändras dess riktning. Detta beror på att ljuset har olika hastigheter i olika medier. På grund av ljusets brytning i t ex en luft-vatten yta så uppfattas ett objektets djup annorlunda än det verkliga djupet. Stråloptik Ljusbrytning Medium 1 i r=i Medium 2 2 Ljuset bryts på grund av att ljuset har olika hastigheter i de olika medierna Riktning ändras 2 i ”Ljuset bryts” Ljusbrytning Medium 1 1 1 Stråloptik Riktning ändras 2 i ”Ljuset bryts” Medium 2 2 Ljusbrytningen bestäms av Snells lag n1 sin 1 = n2 sin 2 Värden på n för olika material finns i tabeller. I ekvationen ovan kallas n för brytningsindex och är definierat som n = [ ljushastighet i vakuum ] / [ ljushastighet i medium ] = c / v Stråloptik Trigonometri h y x sin = y/h, eller: y = h·sin , = arcsin(y/h) cos = x/h, eller: x = h·cos , = arccos(x/h) tan = y/x, eller: y = x·tan , = arctan(y/x) Stråloptik Trigonometri Exempel: En skidlift är 2830 meter lång. I medeltal bildar liften en vinkel på 14,6 relativt horisontalriktningen. Hur högt över startpunkten ligger slutpunkten? Lösning: y = h·sin = 2830·sin(14,6) 2830 ·0,252 713 y=? = 14,6 Svar: Slutpunkten ligger ca 713 m över startpunkten Stråloptik Ljusbrytning Exempel: Antag att ljus faller in mot en gränsyta mellan luft och vatten. Bestäm brytningsvinkeln 2 om infallsvinkeln 1 = 46°. Behandla de två möjliga fallen: a) Ljuset går från luft in i vatten. b) Ljuset går från vatten in i luft. Brytningsindex för luft och vatten är, nluft = 1,00 och nvatten=1,33. Lösning: Se tavlan. Ljusbrytning Stråloptik Energiinnehåll i reflekterad och transmitterad våg Medium 1 Energin bevaras EI = ER + ET 1 1 Medium 2 Storleken på ER relativt ET beror på infallsvinkeln (1) samt de två medierna (dvs n1 och n2). 2 Bilbackspegel Stråloptik Avbländat läge Normalläge öga öga Ljus från bil bakom Ljus från bil bakom Normalläge (dag): Avbländat läge (natt): Utnyttja ljus från silverbelagd Utnyttja ljus reflekterat från gränsyta luft-glas. Reflekterad yta. Reflekterad intensitet intensitet << infallande intensitet. infallande intensitet. Stråloptik Skenbart djup På grund av ljusets brytning i t ex en luft-vatten yta så uppfattas objektets djup annorlunda än det verkliga djupet n2 n1 Skenbart djup: d Verkligt djup: d Skenbart djup då observatören befinner sig rakt ovanför objektet: d = d [ n2 / n1 ] Stråloptik Total internreflektion Antag att ljus faller in mot en gränsyta från vatten till luft med infallsvinkel 1 = 50º. n2 = 1,00 2=? Vad blir brytningsvinkeln i luft? Snells lag: sin2 = [n1 sin1 ] / n2 = = 1,33·sin(50º) = 1,02 >> 1 !! Ej möjligt allt ljus reflekteras 1 n1=1,33 Total internreflektion Stråloptik Total internreflektion n2 n1 c Infallsvinkel mindre än kritisk vinkel Infallsvinkel lika med kritisk vinkel Infallsvinkel större än kritisk vinkel Kritisk vinkel: sinc = sin1 = [n2 sin2 ] /n1 = [n2 sin90º ] /n1 = n2 /n1 För vatten-luft: sinc = n2 /n1 = 1,00/1,33 0,752 c 48,8º Tekniska tillämpningar: Prisma kikare, fiberoptik (sid 791-792 i läroboken). Prisma och dispersion Stråloptik Noggrann analys brytningsindex beror på våglängden (tabell 26.2) Exempel -kronglas: nrött = 1,520, nblått = 1,531 Prisma Ljusbrytningen beror på ljusets våglängd I ett prisma delas vitt ljus upp i ett spektrum av färger Detta kallas för dispersion. Ljusbrytning - linser Brännpunkt Fokus Konvergerande lins f = brännvidd Brännpunkt Divergerande lins Fokus f = brännvidd Stråloptik Stråloptik Bildkonstruktion - konvergerande lins Stråle 1 Initialt parallell med symmetriaxeln, bryts mot, och går igenom, höger brännpunkt F F F F F F Stråle 2 Går initialt genom vänster brännpunkt, går efter brytningen parallellt med symmetriaxeln Stråle 3 Går igenom linsens centrum och bryts ej Stråloptik Bildformering från konvergerande lins • Objektet utanför 2F: Bild som är reell, inverterad och mindre än objektet. Exempel: kamera F • Objektet mellan F och 2F: Bild som är reell, inverterad och större än objektet. • Objektet innanför F: Divergerande strålar, men betraktat mha ett öga Bild som är virtuell, rättvänd och större än objektet. F Exempel: projektor F F Exempel: förstoringsglas F F Stråloptik Ekvationen för en tunn lins do di ho Linsformeln för en tunn lins hi 1/do + 1/di = 1/f F F f Linjär förstoring för en tunn lins m = [bildhöjd / objekthöjd ] = = hi / ho = di / do f • f = brännvidd • do = avstånd till objekt • di = avstånd till bild • ho = objekts höjd • hi = bildens höjd • m = förstoring Stråloptik Linser i kombination Den bild som produceras av en lins utgör objekt för nästa lins. F1 F1 F2 5 cm 3 cm f1 = + 1 cm do1 F2 di1 f2 = + 2 cm do2 di2 Stråloptik Ögats anatomi Ögat När ögat träffas av en Ögonlins Näthinna ljusstråle bryts denna först i hornhinnan. Hornhinna Innanför hornhinnan finns ett vätskefyllt Regnbågshinna område, och där Ögonmuskel bakom regnbågshinnan, linsen, glaskroppen och sist näthinnan. Näthinnan är den ljuskänsliga delen av ögat, bestående av tappar och stavar. Regnbågshinnan är den färgade delen av ögat och kontrollerar mängden ljus som når näthinnan. Öppningen i regnbågshinnan kallas för pupill. Ögats lins har en variabel tjocklek vilken kontrolleras av ögonmuskeln. Stråloptik Ögat Ögats optik Ögat har ett fixt avstånd mellan linsen och näthinnan. För att fokusera objekt på olika avstånd ändras linsens brännvid genom att variera linsens tjocklek. Då objekt på långt avstånd betraktas så är ögonmuskeln avslappnad och linsen är tunn. För att betrakta objekt på nära avstånd spänns ögonmuskeln, vilket innebär att linsen blir tjock. Stråloptik Ögat Närsynthet En närsynt person kan ej fokusera objekt långt bort, eftersom linsen i sitt tunnaste läge har en brännvidd som är för kort. Detta kan kompenseras med en divergerande lins. Divergerande lins Stråloptik Ögat Långsynthet En långsynt person kan ej fokusera objekt nära, eftersom linsen i sitt tjockaste läge har en brännvidd som är för lång. Detta kan kompenseras med en konvergerande lins. Konvergerande lins Stråloptik Ögat Hur stort vi uppfattar ett objekt beror på hur stor objektets bild blir på näthinnan. Detta innebär också att ett objekt som är nära ögat uppfattas som större än om objektet är långt från ögat. Stråloptik Förstoringsglas Bilden av ett objekt kan förstoras genom att använda ett förstoringsglas dvs en konvergerande lins. Vinkelförstoringen av objektet betecknas M och definieras som kvoten mellan vinklarna ´ och (uttryckta i radianer) M = ´/ Vinkelförstoring för ett förstoringsglas M ( 1/f - 1/di ) N Konvergerande lins N = närgräns Stråloptik Mikroskop När en större förstoring, än vad som är möjligt med ett förstoringsglas, behövs, så kan objektet för-förstoras genom att införa en extra lins (objektiv) L fo fo fe fe Öga Vinkelförstoring för ett mikroskop M ( L - fe )·N / ( fo fe ) Lins 1 Objektiv Lins 2 Okular (eyepiece) Stråloptik Teleskop Ett teleskop är ett instrument för att förstora objekt som befinner sig på mycket långt avstånd. Öga Vinkelförstoring för ett teleskop M - fo / fe Lins 1 Objektiv Lins 2 Okular