Vinklar. GVi
advertisement

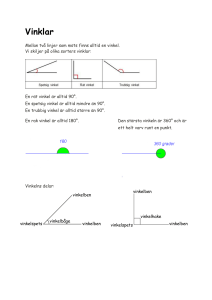
Vinklar. GVi Delområde GVi omfattar följande tre diagnoser: GVi1 Vinklar GVi2 Vinklar, samband GVi3 Vinklar problemlösning Sambandet mellan de olika diagnoserna ser du i strukturschemat nedan. Diagnoserna GVi1, GVi2 och GVi3 är av olika komplexitet, från enkel vinkelmätning till satser om vinklar och problemlösning. GFo 3 Plana figurer GVi 1 Vinklar GVi2 Vinklar, samband GVi3 Vinklar, problemlösnin g Didaktiska kommentarer till delområdet GVi Vinkel är ett centralt begrepp inom såväl den plana geometrin som inom rymdgeometrin. Det är bl.a. med hjälp av vinklarna man kan skilja en romb från en kvadrat och avgöra att vissa parallellepipeder är rätblock. Den räta vinkeln har således en särskild betydelse. En vinkel kan definieras på två sätt, antingen som området mellan vinkelbenen eller som storleken av den vridning som krävs för att lägga det ena vinkelbenet ovanpå det andra. Den senare definitionen brukar vara enklare att förstå för eleverna. I de fall man pratar om området mellan vinkelbenen kan eleverna få (miss-)uppfattningen att längden på vinkelbenen påverkar vinkelns storlek. En vinkel definieras av två ben (en streckad och en grå) som utgår från en gemensam punkt (vinkelspetsen). Figuren visar vinkeln 30º mellan det streckade och det grå vinkelbenet. Vrids det streckade benet ett helt varv är motsvarande vinkel 360º.Om vridningen av ett vinkelben är ett fjärdedels varv är vinkeln 90º, rät vinkel (se figuren) och om vridningen är ett tolftedels varv är vinkeln 30º. Vid mätning med gradskiva gäller det att mäta rätt vinkel, den som markerats med en båge. Det är också viktigt att man direkt kan känna igen vissa vinklar och därmed ange vinklars närmevärden. Sådana vinklar är den räta vinkeln, 90º, en halv rät vinkel, 45º och vinklarna i en liksidig triangel, 60º. Hälften av 60º är 30º. Vid lösning av problem som handlar om vinklar förutsätts att eleverna har en god taluppfattning och behärskar grundläggande aritmetik. Eftersom trianglar, fyrhörningar och andra månghörningar är uppbyggda av sträckor och vinklar är vinklar och vinkelmätning centrala begrepp inom geometrin. Genom att riva av de tre hörnen i en triangel och foga samman dem kan man sluta sig till att vinklarna tillsammans bildar ett halvt varv. Vinklarnas summa är således 180º. Eftersom en fyrhörning är uppbyggd av två trianglar är dess vinkelsumma 360º. I det centrala innehållet för årskurs 7-9 nämns "Geometriska satser och formler och behovet av argumentation för deras giltighet". Detta bör genomsyra undervisningen betydligt tidigare. Genom att, i figuren nedan, utgå från att a + b = 180º och att b + c = 180º finner man t.ex. att och a = c, alltså att vertikalvinklarna är lika stora. . På motsvarande sätt kan man visa att yttervinkeln till en triangel är lika stor som summan av de två motsatta inre vinklarna. På högstadiet bör man följa upp detta med fler satser som exempelvis satserna om bågvinklar och medelspunkstvinklar, vilket i sin tur leder till intressanta egenskaper om trianglar och fyrhörningar som är inskrivna i en cirkel.