4. Inför Nationella Prov

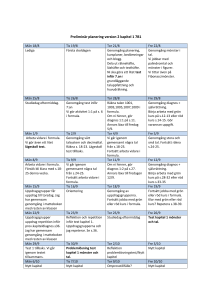
4. Inför Nationella Prov
I detta kapitel kan eleverna testa sina kunskaper, område för område, i uppgifter liknande dem som
finns i nationella prov. Dessa ”diagnosuppgifter” följs upp med uppgifter där eleverna kan reparera
eventuella kunskapsbrister.
Kapitlets upplägg gör det möjligt för eleven att jobba mer självständigt och i egen takt. Det
är du som lärare som bestämmer hur mycket du vill att eleverna ska göra gemensamt. Om du väljer
att låta största delen av eleverna arbeta på egen hand frigör du egen tid och kan ägna dig åt de elever
som riskerar att inte nå målen.
Kapitlet är uppdelat efter läroplanens sex områden:
Område
1. Taluppfattning och tals användning
2. Algebra
3. Geometri
4. Sannolikhet och statistik
5. Samband och förändring
6. Problemlösning
Sida i elevboken
134
142
148
156
164
170
Bilden på s. 133 visar hur ett gult rapsfält separerar en blå himmel från ett grönt fält.
Diagnoser
Varje område startar med en diagnos med uppgifter som liknar nationella provuppgifter. Diagnosen
är uppdelad i tre färgkodade delar. Elever som varit osäkra på t.ex. en grön diagnosuppgift, arbetar
med gröna uppföljningssidor, elever som varit osäkra på en blå diagnosuppgift arbetar med blå
uppföljningssidor osv. Diagnoserna kan som vanligt rättas av dig som lärare eller av eleverna själva.
Diagnos- och uppföljningsschema
Låt gärna eleverna ta hjälp av Diagnos- och uppföljningsschemat på sidan (…) Där kan de fylla i
hur diagnoserna gått och i kommentarsfältet kan antingen du som lärare eller eleverna själva skriva
t.ex. vad de ska tänka på för att utvecklas vidare på bästa sätt.
Betygs- och förmågepoäng
I diagnosernas sista uppgift och hela Diagnos 6 ser eleverna betygspoäng. Till dessa uppgifter
uppmanas eleverna att visa hur de löser uppgiften, så som de uppmanas att göra i nationella
provuppgifter. Låt gärna eleverna jämföra sina svar med kamraters, i grupp eller i helklass. Vid
dessa uppgifter är det särskilt viktigt att tänka på:
- hur eleven löser uppgiften
- vilka kunskaper eleven visar om matematiska begrepp
- vilka metoder eleven väljer och använder
- hur väl eleven redovisar ditt arbete
- hur väl eleven använder ett matematiskt språk
I facit till diagnoserna är förmågorna, som eleven ska utveckla, kopplade till betygspoängen. På
sidan (...) kan du se vad förkortningarna betyder. Till varje diagnosfacit finns även kamrat- och
självbedömning till uppgifterna med betygspoäng.
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Miniräknare
I Diagnos 6 och kapitlets sista område med problemlösning är miniräknare tillåten. Fler uppgifter
med problemlösning finns i kap 6.
I kapitel 4, och framför allt i sista området med problemlösning, förekommer två nya
namn, Nathan och Prim. Namnet Nathan är valt med tanke på kapitelnamnet och Prim för att det är
PRIM-gruppen som konstruerar nationella prov.
Uppföljningssidor
När en diagnos är gjord och rättad vet eleverna vilka typer av uppgifter som de bör arbeta mer med.
Uppföljningssidorna har samma färger som tillhörande diagnosuppgifter. Elever som haft fel på röd
uppgift arbetar med röda uppföljningssidor osv.
Våra kommentarer här i lärarhandledningen till uppföljningsuppgifterna är inte lika
omfattande som den varit i bokens övriga kapitel eftersom inga nya begrepp eller uppgiftstyper
förekommer på uppföljningssidorna. Vi författare kommenterar endast de uppgifter där det kan
finnas tveksamheter i tolkning eller något annat som speciellt behöver lyftas fram.
Facit
Svaren till diagnoserna finns enbart på kommande sidor. Vill du låta eleverna rätta diagnoserna
själva eller att de ska arbeta med själv- och kamratbedömning går det bra att kopiera såväl
diagnosfacit som bedömningsförslagen.
I elevfacit finns svar till uppföljningssidorna. Här skriver vi som vanligt kommentarer eller
alternativa svar till uppgifter där det är extra intressant för eleverna att se samband eller upptäcka
mönster.
Färgkodning
På nästa sida ser du hur vi författare delat upp elevernas diagnoser, och därmed även läroplanens
sex matematiska områden, i mindre delar. Uppdelningen gör det lättare för eleverna att välja
uppföljningsuppgifter.
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Kapitel 4:s sex områden med ytterligare indelningar
1. Taluppfattning och tals användning
 Rationella tal och deras egenskaper.
 Positionssystemet för tal i decimalform. Det binära talsystemet och talsystem som använts i några
kulturer genom historien, till exempel den babyloniska.
 Tal i bråk och decimalform och deras användning i vardagliga situationer.
 Tal i procentform och deras samband med tal i bråk och decimalform.
 Centrala metoder för beräkningar med naturliga tal och enkla tal i decimalform vid överslagsräkning,
huvudräkning samt vid beräkningar med skriftliga metoder och miniräknare. Metodernas användning i
olika situationer.
 Rimlighetsbedömning vid uppskattningar och beräkningar i vardagliga situationer.
2. Algebra
 Obekanta tal och deras egenskaper samt situationer där det finns behov av att beteckna ett obekant tal
med en symbol.
 Enkla algebraiska uttryck och ekvationer i situationer som är relevanta för eleven.
 Metoder för enkel ekvationslösning.
 Hur mönster i talföljder och geometriska mönster kan konstrueras, beskrivas och uttryckas.
3. Geometri
 Grundläggande geometriska objekt däribland polygoner, cirklar, klot, koner, cylindrar, pyramider och
rätblock samt deras inbördes relationer. Grundläggande geometriska egenskaper hos dessa objekt.
 Konstruktion av geometriska objekt. Skala och dess användning i vardagliga situationer.
 Symmetri i vardagen, i konsten och i naturen samt hur symmetri kan konstrueras.
 Metoder för hur omkrets och area hos olika tvådimensionella geometriska figurer kan bestämmas och
uppskattas.
 Jämförelse, uppskattning och mätning av längd, area, volym, massa, tid och vinkel med vanliga
måttenheter. Mätningar med användning av nutida och äldre metoder.
4. Sannolikhet och statistik
 Sannolikhet, chans och risk grundat på̊ observationer, experiment eller statistiskt material från
vardagliga situationer. Jämförelser av sannolikheten vid olika slumpmässiga försök.
 Enkel kombinatorik i konkreta situationer.
 Tabeller och diagram för att beskriva resultat från undersökningar. Tolkning av data i tabeller och
diagram.
 Lägesmåtten medelvärde, typvärde och median samt hur de kan användas i statistiska undersökningar.
5. Samband och förändring
 Proportionalitet och procent samt deras samband.
 Graferförattuttryckaolikatyperavproportionellasambandvidenklaundersökningar.
 Koordinatsystem och strategier för gradering av koordinataxlar.
6. Problemlösning
 Strategier för matematisk problemlösning i vardagliga situationer.
 Matematisk formulering av frågeställningar utifrån vardagliga situationer.
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Diagnos- och uppföljningsschema för kapitel 4 – Inför Nationella Prov
Områden och diagnosuppgifter
Hur gick det?
Uppföljningssidor
1. Taluppfattning och tals
användning
Diagnos 1 (s. 135)
s. 136-137
D1-D4
s. 138-139
D5-D7
s. 140-141
D8-D9
2. Algebra
Diagnos 2 (s. 143)
D1-D3
s. 144-145
D4-D5
s. 146
D6-D7
s. 147
3. Geometri
Diagnos 3 (s. 149)
D1-D3
s. 150-151
D4
s. 152-153
D5-D8
s. 154-155
4. Sannolikhet och statistik
Diagnos 4 (s. 157)
D1-D2
s. 158-159
D3
s. 160
D4-D6
s. 161-163
5. Samband och förändring
Diagnos 5 (s. 165)
D1-D2
s. 166-167
D3
s. 168
D4-D5
s. 169
6. Problemlösning (med
miniräknare)
Diagnos 6 (s. 171)
s. 173-176
D1-D7
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Kommentar
Sidan 135 Diagnos 1 - Taluppfattning och tals användning
Facit till Diagnos 1
D1
a 15 030
D2
50
D3
a3
D4
1100två
D5
a 0,2
D6
b 305 000
Sida i kapitlet med
liknande uppgifter
c 1 500 000
136
136
b 2,6
c 2,58
137
137
b 0,65
1
4 50
2 , 8 , 100
c 0,9
d 1,05
och 0,5
D7
a 300 kr
b 600 kr
D8
708 – 189 ≈ 700 – 200 = 500
D9
a 3 249
b 317
138
138
c 1 200 kr
139
140
c 2 190
d 155
141
Bedömningsförslag till D9 – Diagnos 1
Max 2/0/0 betyder att du maximalt kan få 2 E-poäng, 0 C-poäng och 0 A-poäng. (I denna diagnos
kan du bara få E-poäng.)
P = problem
B = begrepp
M = metoder
R = resonemang
K = kommunikation
M i ”EM” betyder att förmågan M (metoder) ligger på betygsnivå E.
D9 a 3 249
Skriver korrekt svar.
(max 2/0/0)
EM
Redovisar hela lösningen tydligt med uppställning eller annan skriftlig
metod (t.ex. 2000 + 1100 + 140 + 9).
EK
D9 b 317
Skriver korrekt svar
(max 2/0/0)
EM
Redovisar hela lösningen tydligt med uppställning eller annan skriftlig
metod (t.ex. 51 + 200 + 66).
EK
D9 c 2 190
Skriver korrekt svar.
(max 2/0/0)
EM
Redovisar hela lösningen tydligt med uppställning eller annan skriftlig
metod (t.ex. 6 ∙ 300 + 6 ∙ 60 + 6 ∙ 5).
EK
D9 d 155
Skriver korrekt svar.
(max 2/0/0)
EM
Redovisar hela lösningen tydligt med uppställning eller annan skriftlig
620 310
metod (t.ex. 4 = 2 = 155 ).
EK
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 136-137
Vad är ett fyrsiffrigt tal? I facit till uppgift 2 skriver vi:
2 a 9 110
b Minsta fyrsiffriga tal är 1 019. (0029 = 29 är tvåsiffrigt.)
I Prima Formula 4, elevboken, på sidan. 11 tar vi upp problematiken xx-siffriga tal. I
lärarhandledning 4 på sidan 30 förklarar vi orden siffra och tal i vardagliga respektive
matematiska sammanhang. Se speciellt rutan Vardagsspråk och mattespråk kring xxsiffriga tal. På samma sida hittar du också rutan Att skriva 1000 eller 1 000 där vi
behandlar mellanslaget mellan tusental och hundratal.
Uppgift 5. I Lärarhandledning Prima Formula 4, sidan 250 finns ett kopieringsblad, som i
god progression behandlar positionssystemet med hjälp av miniräknarens sifferfönster.
Uppgift 9. I facit skriver vi ut nollor i början av talet, t.ex. 9 a 008090. Så fungerar det på en
besöksräknare. Om uppgiften gällt en miniräknare skulle vi svarat: 8090.
Uppgift 10. Precis som i Prima Formula 4 s. 93-95, belyser vi med hjälp av tallinjer att avrundning
handlar om att ”se vilket tal som ligger närmast”. Mer Överslag och avrundning kan eleverna arbeta
med i nästa kapitel, sidan 190-193.
Uppgift 14-15. Uppgifterna har liknande uppbyggnad som uppgifterna 77-80 i föregående
kapitel. Progressionen i uppgift 14 är tydlig med att alla talen tillhör de olika positionerna.
I uppgift 15 kan eleverna se vad som händer när talet ökar med en enhet.
Sidan 138-139
Här exemplifieras procent, bråk- och decimalform med hjälp av rutor, antal kulor, bilder,
omkrets, sträckor och priser. Dessa och flera andra situationer finns i kapitel 2 och 3 i
Prima Formula 5.
Uppgift 16-17. Eleverna kan se samband mellan uppgifterna 16 och 17 i deluppgifterna a,
b respektive c.
Uppgift 23. Det är nyttigt för eleverna att få se flera olika sorters bilder som
representationer för procenttal. På de två sista raderna, med cirkel eller klocka, kommer
även ungefärliga 33% och 67% naturligt in. I facit svarar vi dock med 3 decimaler
eftersom svaret i näst sista raden ges med tre siffrors noggrannhet.
Uppgift 26-27. Dessa typer av uppgifter finns det gott om i Prima Formula 5 s. 110-112.
I uppgift 27d svarar vi: Ja, för alla priser högre än 0 kr. Eleverna kan prova med olika
värden på bollens pris och konstatera att svaren blir samma. Även med priset x kr kan man
med algebra visa att det stämmer, och därmed gäller det generellt. Dock måste gälla: x < 0.
OM priset är 0 kr, så kan man inte längre tala om att man får rabatt i procent. Exempel:
Jag har satt ut korgar med äpplen, som du får ta så många du vill av, och de är
gratis. Du väljer mellan att ta 12 äpplen direkt eller att plocka 4 st i tre omgångar.
Detta blir samma pris för dig, 0 kr, och det ger dig inte heller någon rabatt i procent
i något av fallen (med falläpplena).
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 140-141
På dessa sidor handlar uppgifterna 28-33 huvudsakligen om Överslag och Avrundning,
med exempel på sådant som tidigare behandlats i Prima Formula 4, sidan 93-98. Mer om
Överslag och avrundning kan eleverna arbeta med i nästa kapitel s. 190-193.
Uppgift 31b. Cesars svar bör bli 5 923.
Tryckfelsnisse:
I elevbokens första tryckning har Cesar skrivit ? 9 0 3 i algoritmens sista rad. Det ska vara
? 9 2 3. (Kanske har Cesar glömt minnessiffran 2?)
Uppgift 38 och 40. Här ska eleverna använda ”skriftliga räknemetoder”. Sådana har
tidigare presenterats i Prima Formula 4 s. 51 och 130-132. Vi har där och på flera andra
ställen i Prima Formula 4-5 sett följande metoder:
T = Tanjas talsortsräkning
A = Algots algoritm (uppställning)
H = Hugos halvering-dubblering
Dessa exemplifierar vi här i ett par exempel.
38a
Metod T: 253 ∙ 3 = 3 ∙ 200 + 3 ∙ 50 + 3 ∙ 3 = 600 + 150 + 9 = 759
Metod A:
253
∙ 3_1
759
Vi visar också hur Tanja kan använda sin metod i en variant på Algots metod för addition,
T och A:
253 ∙ 3 =
600
150
+
9
759
38b
Metod H: 4 ∙ 209 = 2 ∙ 418 = 836
(I uppgift 40b kan eleverna göra på Pollys sätt, Prima Formula 4 s. 54.)
40 b
566 – 475 = 25 + 66 = 91
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 143 Diagnos 2 - Algebra
Facit till Diagnos 2
Sida i kapitlet med
liknande uppgifter
D1
ax+2
b x/2
144
D2
2x + 6 eller 2 ∙ x + 6
144-145
D3
20 st
145
D4
a8
b 2,7
c 100
d 30
146
D5
a x = 17
b x = 13
cx=4
dx=6
146
D6
a 100
b 16
c 15
147
D7
a 17
b 41
c B = 4 ∙ n +1
147
Bedömningsförslag till D7 – Diagnos 2
Lösningar bedöms med E-, C- och A-poäng (kopplade till förmågorna).
P = problem
B = begrepp
M = metoder
R = resonemang
(E/C/A)
K = kommunikation
D7 a 17
Korrekt svar eller bild på mönstret.
(max 1/0/0)
EP
D7 b 41
Korrekt svar.
(max 1/1/1)
EP
Påbörjad lösning, visar t.ex. multiplikation med tio.
CM
Tydlig lösning som beskriver hur hela mönstret växer
(t.ex. ”man multiplicerar figurens nummer med fyra och adderar sen
med ett”).
AK
D7 c B = 4 ∙ n + 1
Korrekt svar
(max 1/1/1)
EP
Förklarar varför formeln passar för figur n.
(t.ex. visar att formeln stämmer för en figur )
CK
Tydlig förklaring varför formeln passar för figur n.
(t.ex. visar att formeln stämmer för minst två olika figurer)
AR
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 144-145
Uppgift 41-42. Här får eleverna starta med uttryck utan bokstäver. I uppgift 42 måste
eleverna ”se upp” och lägga märke till att Bella och hennes tre kompisar ger en fyra i
nämnaren.
Uppgift 43-52. Denna typ av uppgifter har nyligen behandlats i kapitel 3.
Uppgift 53-54. Denna typ av uppgifter förekommer ibland på tester och nationella prov.
Uppgift 54 är lite svårare för att den vänder på förhållandet, så att antalet virvlar v är
mindre än antalet kors k. Vi kan skriva uttrycket 6k = 2v, vilket kan förenklas till 3k = v:
Uppgifterna kan då lösas så här:
54a 7v = 7 ∙ 3k = 21k. Svar: 21 kors.
Eleverna skriver nog hellre så här:
2 virvlar = 6 kors
1 virvel = 3 kors
7 virvlar blir då 21 kors
eller
2 virvlar = 6 kors
7 virvlar blir då 3,5 ∙ 6 kors = 7 ∙ 3 kors = 21 kors
I uppgift 54b ska 6 kors, värda 60 poäng, först översättas till 1 kors värt 10 poäng. Därefter
får man fram att en virvel är värd 3 kors. Vi får alltså 3 ∙ 10 poäng = 30 poäng.
Sidan 146-147
Uppgift 58-59. I en del sammanhang har vi märkt att elever kan ha svårt för uppgifter av
typ 58c och 59c. Därför har vi här lagt dem i en progression så att eleverna själva kan
upptäcka vilket svar som är riktigt och varför.
Uppgift 67. I pratbubblan står ”kvadrattal” och ”kubiktal”. Dessa har eleverna påträffat
flera gånger tidigare, bl.a. på sidan 73. I uppgift a består talföljden av ”triangeltalen” som
förekommer i kapitel 3 sidan 93.
Uppgift 68. Alla tre uppgifter kan ses som exempel på positionssystem. I uppgift a är det
bas 10, i b bas 2 och i c bas 5. Alla tre finns på bild på sidan 112.
Uppgift 70c. Rätt alternativ på formel är B = 3 ∙ n + 1. I detta kapitel skriver vi oftast
formler med utsatt multiplikationstecken. Detta för att nationella prov för skolår 6 gör så. I
kapitel 3, på sidan 105, övergår vi ganska snart till att skriva motsvarande formel utan
multiplikationstecken, S = 3n + 1. Detta gör vi för att eleverna lättare kan förenkla uttryck
då. Samtidigt varnar vi också där, via Felex, för feltolkningar av uttryck av typ 3n.
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 149 Diagnos 3 - Geometri
Facit till Diagnos 3
Sida i kapitlet med
liknande uppgifter
150
D1
aC
bA
cB
D2
aC
bB
cA
D3
a 40 mm
b 10 mm
c 200 mm
D4
151
d 2 mm
151
a t.ex. 152-153
cm
2
6
b t.ex.
cm
2
6
cm
c
1,5
1,5
d Störst area har kvadraten med sidan 3,5 cm.
Störst area med endast heltal, har en rektangel med sidorna 3 och 4 cm.
cm
3
3,5
4
3,5
D5
a 250
b 1,5
c 250
D6
a 180º
b 90º
c 15º
D7
a 30º
b 330º
154
d 60º
155
155
D8 5 h 45 min
156
Bedömningsförslag till D8 – Diagnos 3
Lösningar bedöms med E-, C- och A-poäng (kopplade till förmågorna).
P = problem
B = begrepp
M = metoder
R = resonemang
D8 5 h 45 min
Korrekt svar.
(E/C/A)
K = kommunikation
(max 1/1/0)
EM
Tydlig redovisning med korrekt svar och enhet
(t.ex. visar att skoldagen är 15 min kortare än 6 h eller med addition:
40 min + 5 h + 5 min = 5 h 45 min).
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
CK
Sidan 150-151
Uppgift 73-75. På dessa uppgifter kan eleverna kolla sina svar via ”formeln” som
användes i samband med uppgift 7 sidan 53: B + H – K = 2.
a- uppgifterna: 6 + 8 – 12 = 2
b- uppgifterna: 4 + 4 – 6 = 2
c- uppgifterna: 5 + 6 – 9 = 2
d- uppgifterna: 8 + 12 – 18 = 2
Uppgift 82d. Här får eleverna se upp, och undvika svaret 360º. Därmed kan de också
repetera vad de upptäckte redan i Prima Formula 4 sidan 167, nämligen att vinkelbenens
längd inte påverkar vinkelns storlek. Uppföljning sker i uppgift 101.
Sidan 152-153
Uppgift 90. Det teoretiska värdet på höjden h i den liksidiga triangeln är 2 33,464
. Ett
sådant teoretiskt värde behöver eleverna och du inte alls tänka på, men kan vara bra att
känna till när eleverna ska mäta i uppgift 92b.
Uppgift 92b. Det teoretiska värdet på höjden h i den liksidiga triangeln med sidan 6 cm
cm

5
,
196
cm
är 33
. Om eleverna ritat triangeln rätt bör de få svaret till 52 mm, men
givetvis kan det skilja på någon millimeter.
Sidan 154-155
Uppgift 101. Vinkel C har längst vinkelben och ”ändå” minst vinkel.
Uppgift 106-107. Denna typ av uppgifter introducerade vi i Prima Formula 5, sidan 13, där
vi genom uppgift 31 uppmärksammade eleverna på att det finns bättre strategier vid denna
typ av beräkningar av tider, än att räkna ”en timme i taget”. Se t.ex. rutan med ”smarta
metoder i Lärarhandledning 5, sidan 27.
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 157 Diagnos 4 – Sannolikhet och statistik
Facit till Diagnos 4
D1
a 1/4 (25%)
D2
8 st
D3
a4
b 17
D4
a5
b6
D5
a1
b 2,5
Sida i kapitlet med
liknande uppgifter
b 1/8 (12,5%) c 3/8 (37,5%)
158-159
159
c 30
160
161
c3
D6 Sanna är 168 cm lång.
162
162-163
Bedömningsförslag till D6 – Diagnos 4
Lösningar bedöms med E-, C- och A-poäng (kopplade till förmågorna).
P = problem
B = begrepp
M = metoder
R = resonemang
(E/C/A)
K = kommunikation
D6 Sanna är 168 cm lång
Redovisar en påbörjad lösning som visar kunskap om medelvärde.
(t.ex. prövar sig fram eller gör beräkningen 3 ∙ 160 cm).
(max 0/1/2)
CB
Löser hela uppgiften med korrekt svar. T.ex. prövar sig fram.
AP
Använder effektiv metod
(t.ex. visar att Adam och Cesar tillsammans är 8 cm kortare än
medellängden eller visar hur Sannas längd kan bestämmas med
redovisning liknande denna: 3 ∙ 160 cm = 480 cm.
Sanna (cm) = 480 – (154 + 158) =480 – 312 = 168).
AM
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 158-159
Uppgift 117. Eleverna kan se sannolikheterna genom att göra en tabell liknande den i
uppgift 116, men nu med 6x6 rutor i stället för 4x4. Detta finns även i Prima Formula 5,
sidan 146.
Uppgift 118-119. Dessa uppgifter är exempel på området kombinatorik och är en av många
olika typer av multiplikation. En introduktion finns i Prima Formula 4, sidan 133. I kap 6,
sidan 206 (uppgift 16-19), finns fler uppgifter som handlar om kombinatorik.
Sidan 160-161
Uppgift 126. Milos metod, som egentligen är en enkel formel för medelvärdesberäkning,
introduceras i Prima Formula 5, sidan 172.
Uppgift 128b. Detta vanliga fel som Felex gör i denna uppgift, får eleverna förståelse för
med hjälp av nästa uppgift, 129. Att nollan har stor betydelse visade vi även i Prima
Formula 5, på sidan 182, under rubriken ”Nollans betydelse”.
Sidan 162-163
Uppgift 129. Detta är en typ av ”självreglerande” uppgifter för de elever som själva gör
Felex-fel som i uppgift 128b eller tänker likt Felex gjorde i den uppgiften.
Uppgift 130-132. Dessa uppgifter visar i lämplig progression hur man i samband med
medelvärde endast behöver 2 av de 3 ingående komponenterna.
Uppgift 133. I facit skriver vi:
70º (Behöver du veta att ”medelvärdet är 60º”?)
Förhoppningsvis vet eleverna sedan tidigare att vinkelsumman i en triangel är 180º.
Men denna formulering i facit kan kanske få elever att fundera över om alla upplysningar i
en uppgift behövs för att den ska kunna lösas.
Uppgift 137. Den här uppgiften är i princip samma som föregående uppgift. En liten
skillnad är att värdena nu anges i meter, en stor skillnad är att värdena presenteras i en
frekvenstabell. Vid uppgifter med sådan tabell har vi författare sett många utförda ”Felexfel” av våra elever. Denna typ av fel visar vi i samband med uppgift 141.
Uppgift 141c. Här kan det lätt förekomma ett typiskt Felex-resonemang:
”Av frekvenserna 4 + 5 + 9 + 1 + 1 får jag summan 20. En sådan summa brukar
divideras med något enkelt tal. Ska jag välja 4 eller 5 dagar? Om jag väljer 4 dagar får
jag medelvärdet 20/4 = 5. Om jag väljer 5 dagar får jag medelvärdet 20/5 = 4. … .”
Båda dessa felexvärden ligger långt ifrån det riktigt beräknade medelvärdet: 30/20 = 1,5.
Det enklaste sättet för eleverna att få fram värdet 30, är att göra en ny kolumn till höger om
Frekvenskolumnen och fylla i värdena 0, 5, 18, 3 och 4 som ger summan 30. Denna
summa ska därefter divideras med antalet elever (20) som deltog i undersökningen.
Vid uppgifter med liknande tabell har vi sett många utförda Felex-fel, högt upp i skolåren,
även i gymnasieskolan. I Prima Formula 5, sidan 197, visar Felex detta vanligt förekommande fel. I
Lärarhandledning 5, sidan 112, beskriver vi en Aktivitet som kan få eleverna att själva upptäcka hur
man gör för att använda en given frekvenstabell rätt, och t.ex. göra en ny kolumn till höger.
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 165 Diagnos 5 – Samband och förändring
Facit till Diagnos 5
Sida i kapitlet med
liknande uppgifter
1
D1
a 6 ägg
b 7 2 dl
D2
a 25 cl
b 20 cl
c 50 cl
D3
a 20 kr
b 40 kr
c 4 kr
D4
a (1, 3)
b (-2, 2)
c (0, -3)
D5
a
Vikt
1 kg
2 kg
3 kg
4 kg
5 kg
D5 bc
166
d 5 cl
167
168
d (-1, -1)
b-c t.ex.
169
169
Pris
40 kr
80 kr
120 kr
160 kr
200 kr
(max 1/1/1)
Bedömningsförslag till D5 – Diagnos 5
Lösningar bedöms med E-, C- och A-poäng (kopplade till förmågorna).
P = problem
B = begrepp
M = metoder
R = resonemang
(E/C/A)
K = kommunikation
D5 a
Korrekt tabell (se exempel i facit ovan).
(max 1/0/0)
EM
D5 b
Påbörjat diagram som visar vikt (x-axel) och pris (y-axel).
(max 1/1/1)
EK
Diagram med tydliga axlar (med gradering) och rätt utsatta punkter.
CM
Bra strategier för gradering av axlar, t.ex. valda så att diagrammet får lagom
plats
(se exempel i facit ovan).
AP
D5c
Korrekt linje genom origo (se exempel i facit ovan).
(max 0/1/0)
CM
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 166-167
Uppgift 142-144. Eleverna kan på dessa uppgifter kontrollera (eller komma fram till) sina
svar genom att i c-uppgiften addera svaren i a och b. I d-uppgiften kan de på liknande sätt
addera a och c.
Uppgift 153-161. Den här typen av proportionella samband, som innehåller förhållande x:y, kan
vara svåra för många elever. Här får därför eleverna god hjälp av ritade figurer till varje uppgift. De
får även arbeta med flera olika förhållanden.
I uppgift 157d får de se att svaret kan visa det ungefärliga värdet 33 cl.
I uppgifterna 159-160 kan eleverna kontrollera (eller komma fram till) sina svar
genom att i c-uppgiften lägga svaret mitt emellan svaret i a och b.
Sidan 168-169
Uppgift 165b. I facit skriver vi:
b 36 kr (I diagrammet kan du se att priset för 10 hg är 60 kr. 1 hg kostar då 6 kr. 6 hg
kostar 36 kr.)
Vi skriver så för att uppmärksamma eleverna på att det är svårt att avläsa värdet 36 i
diagrammet, och att man då får en säkrare avläsning om man avläser vid ett större värde på
axlarna.
Uppgift 168. Som vi tidigare påpekat, finns det i Del 5 två blad som heter ”Tolka
diagram 1-2”. Sådana diagram, liknande uppgift 168, förekommer ofta i olika tester som
t.ex. nationella prov.
Uppgift 170. I facit har vi, i förhållande till uppgift 169, förlängt axlarna så att eleverna
även i diagrammet tydligt kan se svaret till c-uppgiften.
b
c 480 kr
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 171-172 Diagnos 6 - Problemlösning
Facit till Diagnos 6
sidor i kapitlet med
liknande uppgifter
D1
0,5 m2 (500 cm2)
173-176
D2
324 cm
173-176
D3
a t.ex. tre frukter eller en glass och en frukt
173-176
b 40 – (10 + 12 + 5) = 13
c 108 kr
173-176
D4
a hälften (1/2, 50%, 12/24)
b 15 st
173-176
D5
t.ex. 9 st vardera eller 10 och 8. (Eller 11 och 7, 12 och 6, …)
173-176
D6
Bella 1 st, Adam 4 st, Nathan 4 st och Prim 8 st (om totalt 17 st glas)
173-176
Tryckfelsnisse:
I bokens första tryckning står det att kompisarna dricker 17 glas saft tillsammans. Det ska
vara 19!
Bedömningsförslag till D6 – Diagnos 6
Lösningar bedöms med E-, C- och A-poäng (kopplade till förmågorna).
P = problem
B = begrepp
M = metoder
R = resonemang
(E/C/A)
K = kommunikation
D1 0,5 m2 (5 000 cm2)
Korrekt svar.
(max 0/2/1)
CP
Tydlig redovisning.
CK
Använder effektiv metod. Visar att skylten täcker halva rutnätet.
AM
D2 324 cm
Redovisar en påbörjad lösning. Försöker t.ex. bestämma 1/9 av repet.
(max 0/2/1)
CB
Använder effektiv metod även om svaret inte är korrekt (redovisar en
division och får fram att 1/9 av repet är 144/4 = 36).
CM
Löser hela uppgiften med korrekt svar.
AP
D3 a t.ex. tre frukter eller en glass och en frukt
Ger ett korrekt förslag.
(max 2/0/0)
EP
Ger två korrekta förslag.
EP
D3 b 40 – (10 + 12 + 5) = 13
Redovisar en lösning som visar att ”Dagens erbjudande” är med
(max 1/1/0)
EP
Tydlig redovisning där hela uträkningen är med, t.ex. 40 – (10 + 12 + 5) = 13
CK
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
D3 c 108 kr
Påbörjad lösning, t.ex. tecknar en multiplikation.
(max 1/1/1)
EM
Korrekt svar.
CP
Tydlig redovisning med korrekt svar.
AK
D4 a Hälften (1/2, 50%, 12/24)
Påbörjad lösning, t. ex påbörjad addition av totala antalet glassar.
(max 1/1/0)
EB
Tydlig redovisning med korrekt svar.
CK
D4 b 15 st
Påbörjad lösning där det framgår att 1/4 av glassen är jordgubbssmak.
(max 0/2/1)
CP
Tydlig redovisning även om svaret inte är korrekt.
CK
Tydlig lösning med korrekt svar.
AP
D5 De säljer t.ex. 9 st vardera eller 10 och 8.
Redovisar ett förslag som är korrekt.
(max 2/1/1)
EM
Redovisar två korrekta förslag.
EP
Använder lämplig metod för att få fram möjliga förslag (visar t.ex. att
Adam och Bella har sålt 18 glassar tillsammans).
CM
Tydlig metod som visar att flera andra förslag kan hittas på samma sätt.
AR
D6 Bella 1 st, Adam 4 st, Nathan 4 st och Prim 8 st (om totalt 17 st glas)
(max 0/2/1)
Påbörjad lösning (t. ex stämmer förhållandena mellan kompisarnas antal glas).
CB
Löser hela uppgiften med korrekt svar.
CP
Använder effektiv metod (t.ex. tabell eller algebraiskt uttryck) T.ex.
b + (b + 3) + 4 + 2b = 17, där b = Bellas antal glas = 1 st.
AK
D7 efter 6 månader
Påbörjad lösning (jämför t.ex. syskonens pengar efter några månader).
(max 1/1/1)
EM
Redovisning och slutsats som leder fram till korrekt svar.
CK
Använder effektiv metod (t.ex. gör tabell eller tecknar ekvation) med korrekt svar. AP
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB
Sidan 173-176
I samband med kommentarer till ”Lösa problem” (Del 2 i Prima FORMULA
lärarhandledning 4, 5 och 6) har vi beskrivit de tio tydligast förekommande strategierna vid
problemlösning. Dessa tio strategier kommer eleverna även ha möjlighet att upptäcka,
använda och utveckla i kapitel 6 i elevboken för åk 6.
Problemlösningsstrategier
1. Upptäcka mönster
2. Göra tabell
3. Rita bild
4. Gissa och kontrollera
5. Leta systematiskt
6. Granska villkoren
7. Börja bakifrån
8. Rita hjälplinjer och flytta delar
9. Använda ekvation
10. Förenkla problemet
Uppgift 174. Ett sätt att redovisa hur man kommit fram till beräkningen 12 ∙ 55 kr = 660
kr är att Göra tabell (strategi 2). I tabellexemplet nedan har alla 14 pizzor skrivits in. När var
femte pizza, som är gratis, står inom parentes visas det tydligt att det är 12 pizzor kvar att
betala för.
1 2 3 4 (5)
1 2 3 4 (5)
1234
Uppgift 178. I facit skriver vi:
178 T.ex. 68 barn och 34 vuxna eller 100 barn och 50 vuxna.
Paret av tal 68 + 34, är lägsta tänkbara heltal för att där ska finnas ”hundratals
människor”.
Tryckfelsnisse:
I uppgift 179 d är priset fel. Det rätta priset är 67 kr.
I uppgift 181 har rektangelns bas fallit bort. Bas = 10 cm.
Uppgift 186. Eleverna kan komma fram till svaren genom att Gissa och kontrollera
(strategi 4), men efter att de har arbetat med kapitel 3 vill de kanske hellre Använda
ekvation (strategi 9). De kan i så fall kanske utgå från att Elvira äter e rätter och teckna
ekvation utifrån hur många rätter som äts tillsammans av Elvira + Tanja + pappa +
mamma.
Ekvation: e + 2e + e + 2 + 4 = 18
4e + 6 = 18
e=3
Uppgift 184 och 187. Eleverna kan lösa uppgifterna genom att Göra tabell (strategi 2).
De kan också Använda ekvation (strategi 9).
Uppgift 184: 2600 + 100x = 2200 + 200x
Uppgift 187: 60 – 10x = 40 – 6x
Fler liknande uppgifter finns i kapitel 6, s. 210, uppgift 45-47.
Prima Formula 6 lärarhandledning
Får kopieras! © Bo Sjöström, Jacob Sjöström och Gleerups Utbildning AB