Polarisation

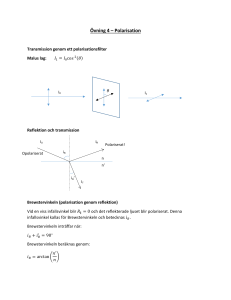
Institutionen för Fysik
Regina Larsson
2005-02-08
Vågrörelselära och Optik B
Polarisation
Syfte
Syftet med denna laboration är att lära sig om ljusets polarisation. Du kommer att se
exempel på opolariserat-, linjärt- och cirkulär polariserat ljus. Exempel på komponenter
som kan ändra ljusets polarisation ingår också att se i denna laboration.
För att få en så effektiv och lärorik laboration som möjligt, bör du läsa om
polarisation(i Hecht kapitel 8 eller i bifogad ”Teori” bilaga) innan laborationstillfället.
Institutionen för Fysik
Regina Larsson
2005-02-08
Vågrörelselära och Optik B
Laborationsdel
Polarisationsfilter
Till nedanstående två moment ska ni använda ett polarisationsfilter.
1)
Bestäm polarisatorns transmissionsaxel genom att använda polariserat ljus
som ni vet polarisationen på. (Hint: använd ljus som reflekterats från ett
dielektrika)
2)
Vad vet vi om ljus som har passerat polarisatorn? (Hint: Vilken polarisation
får ljus från en opolariserad källa? Vad sker med intensiteten hos detta ljus i
en idealisk polarisator? Har polarisationen något vinkelberoende?)
Undersök om transmissionsaxeln är densamma i de polarisationsfilter ni har fått ut.
Använd sedan två av dem i uppgiften nedan. Det första sätter ni i en fast position, vilket
medför att det opolariserade ljuset från lampan nu har en polarisation som är definierat av
filtret. Vi kan uppfatta systemet med lampan och den första polarisatorn som en källa för
linjärt polariserat ljus. Vi ska nu undersöka hur linjärt polariserat ljus transmitteras
igenom ett polarisations filter.
3)
Placera lampan, de två polarisationsfiltren och den vita skärmen på den
optiska bänken så att ljuset går igenom polarisationsfiltren och kan ses på den
vita skärmen. Beskriv huruvida ljusets intensitet varierar när vinkeln mellan
de båda filtren varieras. Rita ljusintensiteten som funktion av vinkeln mellan
polarisatorerna. Hur överensstämmer det uppmätta med Maulus lag (Ekv.3,
s.7)? Vilken period har funktionen?
I uppgift 2 påstods det att ljus som passerat en polarisator får samma polarisation som
filtrets transmissionsaxeln. Vi ska i uppgift 4 försöka att visa detta. Till detta ska vi
använda samma uppställning som i uppgift 3. Ställ de båda polarisatorerna så att inget
ljus transmitteras.
4)
Placera ännu ett polarisations filter emellan de redan två uppställda (se
figuren nedan). Observera huruvida ljusets intensitet på skärmen varierar som
funktion av det mellanliggande filtrets vinkel. Uttryck den utgående
intensiteten som funktion av vinkeln om den infallande intensiteten är I0.
Vilken vinkel har det mellanliggande filtret då vi får maximal transmission?
2
Institutionen för Fysik
Regina Larsson
5)
2005-02-08
Vågrörelselära och Optik B
Tänk ut och genomför ett experiment där ni bestämmer ljusets polarisation
efter den andra polarisatorn.
Kvartsvågsplattor
I följande uppgifter ska ni undersöka hur en kvartvågsplatta (λ/4) påverkar ljus.
6)
Placera lampan, en kvartsvågsplatta och skärmen på den optiska bänken. Får
den transmitterade ljuset något vinkelberoende?
7)
Är ljuset efter kvartvågsplattan linjärt polariserat? (Hint: Placera en
polarisator mellan kvartvågsplattan och den vita skärmen.)
Nu ska vi undersöka om en kvartvågsplatta påverkar ljus som redan är polariserat.
Placera polarisatorn efter lampan.
8)
Blir det någon förändring i intensitet när kvartvågsplattan roteras i förhållande
till polarisatorn?
3
Institutionen för Fysik
Regina Larsson
2005-02-08
Vågrörelselära och Optik B
Nu ska uppställningen innehålla två polarisatorer, en på vardera sida om
kvartvågsplattan. Den andra polarisatorn ska vara roterad 90 grader i förhållande till den
före kvartvågsplattan.
9)
Förändras intensiteten när kvartvågsplattan roteras? Förklara!
10) Ställ in kvartvågplattan så att transmissionen är maximal. Rotera därefter
polarisatorn närmast skärmen. Förändras intensiteten? Är ljuset opolariserat?
Tillför ytterligare en kvartvågsplatta i samma vinkel och efter den första.
11) Undersök ljusets polarisation med hjälp av polarisatorn närmast skärmen.
12) Vad händer med ljusets polarisation om den andra kvartvågsplattan roters till
90 grader jämfört med den första?
13) Tänk ut en metod för att avgöra om ljus är opolariserat eller cirkulär
polariserat.
Optisk aktivitet
14) Fyll en glascylinder med vatten och socker. Denna sockerlösning är ett optiskt
aktivt ämne dvs det kan rotera ljusets polarisation. Verifiera detta genom att
låta polariserat ljus gå igenom sockerlösningen och uppskatta hur mycket
polarisationen roteras. Observera även hur det transmitterade ljusets färg
förändras med vinkeln emellan de båda polarisatorerna.
4
Institutionen för Fysik
Regina Larsson
2005-02-08
Vågrörelselära och Optik B
Polarisation vid reflektion
Nu ska vi hitta Brewstervinkeln, infallsvinkeln som karakteriseras av att allt reflekterat
ljus är polariserat. Vi kan bestämma vinkeln genom att låta polariserat ljus med
polarisationen vinkelrätt mot infallsytan träffa en glasyta. Vi vet att då vi har Brewstervinkeln kommer inget av ljuset att reflekteras.
15) Bestäm Brewster vinkeln för den svarta glasskivan. Lämplig uppställning ses i
figuren överst på andra sidan.
16) Beräkna glasskivans brytningsindex.
Om ni istället för polariserat ljus använder opolariserat ljus, kommer ni att se att allt det
reflekterade ljuset är polariserat.
17) Ändra uppställning så att det infallande ljuset är opolariserat och verifiera att
det reflekterade ljuset är polariserat.
Ljus som transmitteras igenom en glasplatta som är inställd i Brewstervinkeln, kommer
också delvis att bli polariserat. Om ljuset passerar många glasplattor kommer det
transmitterade ljuset att gradvis bli mer och mer polariserat.
18) I labbet finns ett antal objektglas som är sammanfogade. Låt opolariserat ljus
infalla mot dessa i Brewstervinkeln. Vilken polarisation har det
transmitterade ljuset?
Rayleight spridning
Fyll en genomskinlig plastbalja med vatten och tillför lite såpa. Vi kommer i denna del att
se hur ljus sprids mot tvållösningen.
19) När pratar man om ”Mie” spridning och när är det tal om Rayleight
spridning?
20) Karakterisera hur ljusets färg ändras när ljuset går igenom tvållösningen.
5
Institutionen för Fysik
Regina Larsson
2005-02-08
Vågrörelselära och Optik B
Bilaga - Teori
Polarisationsformer
1.1 Linjär eller planpolariserat ljus
Ljus där den elektromagnetiska vågens E-fältvektor
ligger i ett plan kallas linjär eller planpolariserat ljus.
Se Figur 1.
I det allmänna fallet är både Ey och Ez ≠ 0.
Komponenterna är proportionella mot varandra med
fasskillnaden :
∆Φ = ± nπ , n = 0 ,1,2, . ..
(1)
Figur 1 Linjärt polariserat ljus
1.2 Cirkulärpolariserat ljus
En cirkulärpolariserad våg består på samma sätt av två
vågor linjärt polariserade vinkelrätt mot varandra och
med samma amplitud men fasförskjutna:
∆Φ = ± π / 2
(2)
Konvention för högerpolariserat ljus: Ljuskällan
betraktas framifrån. Om den resulterande E-vektorn i
ett fixt plan ⊥ utbredningsriktningen roterar medurs så
är ljuset högerpolariserat (d.v.s. om vågen utbreder sig
rakt emot en betraktare och E-vektorn roterar medurs
så är ljuset högerpolariserat). Se Figur 2.
Figur 2 Cirkulärt höger polariserat
ljus
6
Institutionen för Fysik
Regina Larsson
2005-02-08
Vågrörelselära och Optik B
1.3 Elliptiskt polariserat ljus
Linjär och cirkulärpolariserat ljus är
specialfall av elliptiskt polariserat ljus. I det
allmänna fallet är antingen E x ≠ E y och
eller E x = E y och
∆Φ ≠ ± nπ , n = 0,1, 2,...
∆Φ ≠ ± n ⋅ π 2 , n = 0,1, 2,...
Det kan då se ut som i Figur 3 i det
allmänna fallet. För ett antal givna
fasförskjutningar mellan de två vinkelräta
komponenterna E x och E y får man de
Figur 3 Elliptiskt polariserat
polarisationstillstånd som visas i Figur 4.
orienterat vinkeln α mot x-axeln.
ljus
Figur 4 Polarisationstillstånd
1.4 Opolariserat ljus
Opolariserat ljus kan betraktas som en
superposition av många slumpmässigt
linjärpolariserade vågor där det inte finns
någon korrelation mellan dessas faser eller
amplituder. Man kan representera detta
med två stycken linjärpolariserade vågor
med samma amplitud och slumpmässig
fasskillnad se Figur 5. Detta ger en riktig Figur 5 Representation av opolariserat ljus.
beskrivning av vågens egenskaper om man
betraktar ett större antal perioder.
1.5 Malus´ lag
En polarisator släpper endast igenom den komponent som är vinkelrät mot polaroidens
absorptionsriktning. Detta innebär att en ideal polarisator släpper igenom hälften av
intensiteten av infallande opolariserat ljus. Om en andra polarisator placeras med
genomsläppsriktningen vinkeln θ relativt den första blir utgående intensitet :
I=
I0
cos 2 θ
2
(3)
där I 0 är den infallande intensiteten.
7
Institutionen för Fysik
Regina Larsson
2005-02-08
Vågrörelselära och Optik B
1.6 Rayleighspridning
Då ljus av våglängden λ faller in mot partiklar med en storlek << λ utsänder dessa i sin
tur strålning så att ljuset sprids. Den spridda intensiteten beror av λ enligt :
I s ∝ λ−4
(4)
Att himlen är blå beror på att molekylerna i luften sprider blått ljus mer effektivt, enligt
Ekv.4. Ljus som sprids i olika riktningar har olika polarisationstillstånd. Vi kan se av
Figur 6 att ljus som sprids vinkelrätt mot infallsriktningen är helt linjärpolariserat med
polarisationsriktningen i ett plan vinkelrätt mot infallsriktningen.
Figur 6 Opolariserat ljus spritt mot en molekyl.
8
Institutionen för Fysik
Regina Larsson
2005-02-08
Vågrörelselära och Optik B
Att åstadkomma polariserat ljus
Vi har bara några enstaka ljuskällor som direkt ger linjärpolariserat ljus, exempelvis vissa
lasrar. När man skall ordna med linjärpolariserat ljus så måste man i regel tillgripa något
slags filter för att separera ut en linjär komponent ur opolariserat ljus. Det finns i
huvudsak tre fenomen att utnyttja: dikroism (selektiv absorption), reflektion och
dubbelbrytning.
2.1 Dikroism
Vissa molekyler har förmåga att absorbera den fältkomponent som ligger parallellt med
molekylens
utsträckning. Detta beror på att det finns elektroner som är mer eller mindre fria att röra
sig i molekylens längdriktning. I icke metalliska material är de elektroner som fungerar
som dipoler inte fria, vilket medför att den våg som de genererar inte är ur fas med den
infallande vågen. Därför så kommer den infallande vågen inte att totalt utsläckas, men
dess energi kommer att gradvis absorberas. Absorptionen beror då på polarisatorns
tjocklek och ljusets våglängd. I de vanligaste polarisatorerna är absorptionen lägre vid
kortare våglängder. Detta kan visas genom att korsa två polarisatorer och man kan se att
en aning blått ljus slipper igenom. Se figur 7.
2.2 Polarisation genom reflexion
Fresnels ekvationer ger att om summan
och
av
infallsvinkeln
θi
0
brytningsvinkeln θ t är 90 (d.v.s. när
den reflekterade och transmitterade
strålen är vinkelräta mot varandra),
kommer den reflekterade vågen att vara
linjärpolariserad vinkelrätt mot infalls
planet, se Figur 8. Detta fenomen
kommer sig av att en elektron som
svänger utefter en linje ger upphov till
ett oscillerande elektriskt dipolfält och
den avger ej elektromagnetisk strålning
i
svängningsriktningen.
Fresnels Figur 7 E-fältets dämpning i en polarisator.
ekvationer beskriver vad som sker när
en plan elektromagnetisk våg infaller mot en
gränsyta mellan två olika dielektrika. Ekvationerna
θi θr
relaterar den reflekterade och den transmitterade
vågens intensiteter med den infallandes som
n1
funktion av infallsvinkel θ i och transmissionsvinkel
n2
θ t . För den reflekterade vågen gäller när E-fältet är
parallellt med infallsplanet:
R/ / =
tan 2 ( θ i − θ t )
tan 2 ( θ i + θ t )
(5)
θt
Figur 8 Polarisationsvinkeln
9
Institutionen för Fysik
Regina Larsson
2005-02-08
Vågrörelselära och Optik B
När E-fältet är vinkelrätt mot infallsplanet:
R⊥ =
sin 2 ( θ i − θ t )
sin 2 ( θ i + θ t )
(6)
Om villkoret θ i + θ t = 90o är uppfyllt så gäller R/ / = 0 och man kan då härleda Brewsters
lag:
θ i = θ B = arctan
n2
n1
(7)
där θ B kallas för Brewstervinkeln eller polarisationsvinkeln.
2.3 Kvartsvågsplattan
Kvartvågsplattan är en anordning som ger ett relativt fasskift på ∆ϕ = π / 2 mellan två
ortogonala komponenter i en plan våg. De två vågorna utbreder sig i medium med olika
brytningsindex och har därmed också olika våglängd och olika hastighet. Fasändringen är
därför inte lika stor för de båda vågorna. I en kvartsvågsplatta är optiska axeln
(symmetrilinje i kristallen) parallell med plattans plan. Extraordinäravågen (eo-vågen)
svänger parallellt med optiska axeln medan ordinäravågen (o-vågen) svänger vinkelrätt
mot denna axel, se Figur 9. För en kvartsvågsplatta är fasskillnaden mellan den ordinära
vågen och den extraordinära vågen:
π ± nπ , n = 0,1, 2,...
2
(8)
Kvartsvågsplattor är ofta tillverkade av en polymer där vi har ett riktningsberoende
brytningsindex.
Resultanten mellan E x och E y roterar då med vinkelfrekvensen ω. Vi har fått
cirkulärpolariserat ljus. I de kvartsvågsplattor som vi har i den här laborationen är
λ / 4 = 140 nm .
Figur 9 Fälten i kvartsvågsplattan för ett givet ögonblick.
10