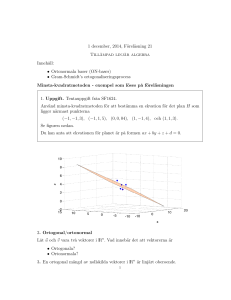
Ortogonala mängder Sats 4
advertisement

Ortogonala mängder
En mängd vektorer {u1, u2, . . . , up} är en ortogonal mängd om varje vektor i mängden
är ortogonal mot alla andra, dvs ui • uj = 0
då i 6= j.
Sats 4
Om S = {u1, u2, . . . , up} är en ortogonal
mängd av vektorer skilda från nollvektorn 0, så är S linjärt oberoende och
därmed en bas för Span(S).
Ortogonala baser
En ortogonal bas för ett underrum W , är en
bas för W som också är en ortogonal mängd.
Sats 5
Låt {u1, u2, . . . , up} vara en ortogonal bas
för W . För varje vektor y ∈ W gäller då
y = c 1 u 1 + c 2 u 2 + · · · + c p up
där vikterna c1, c2, . . . , cp ges av
y • ui
ci =
.
ui • u i
Ortogonal projektion
Ortogonala projektionen av y på u ges av
ŷ =
y•u
u
u•u
Komposanten av y som är ortogonal mot u
ges av
y•u
z=y−
u
u•u
Ortonormerade mängder
En mängd vektorer {u1, u2, . . . , up} är en ortonormerad mängd om det är en ortogonal
mängd av enhetsvektorer.
Om mängden är en bas för ett underrum W
säger vi att det är en ortonormerad bas för
W.
Sats 6
En m × n-matris U har ortonormerade kolonner om och endast om U T U = I.
Sats 7
Om U är en m × n-matris med ortonormerade kolonner, och x, y ∈ Rn, så är
a. kU xk = kxk
b. (U x) • (U y) = x • y
c. (U x) • (U y) = 0 ⇔ x • y = 0