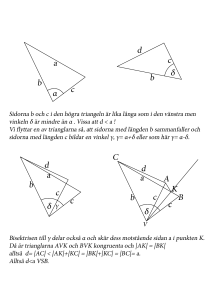
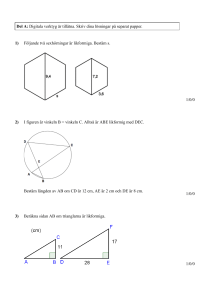
Likformighet och skala
advertisement

Lars Madej [email protected] Förhållande Skala Längd-, area- och volymskala Likformighet Kongruens Vi kan prata om ett förhållande 1:7 ◦ T.ex. blanda saft: 1 del saft, 7 delar vatten ◦ Saften är alltså en åttondel av hela vätskan När vi istället säger skala 1:7 betyder detta att något är förminskat 7 ggr. ◦ Det vill säga bilden är en sjundedel av originalet Förhållande och skala skrivs alltså på samma sätt, men innebär olika saker Förhållandet mellan blå och röd linje är 1:3, vilket innebär att röd linje är 3 ggr så stor som den blå linjen. Vi kan också säga att förhållandet mellan röd och blå linje är 3:1 Nedan är den blå linjen ovan uppskalad och har blivit 4 gånger så lång, dvs skala 4:1 Skrivsätt ◦ 1:100 innebär en förminskning 100 gånger ◦ 3:1 innebär en förstoring 3 gånger Vi kan även till exempel skriva ◦ 3:2 vilken innebär en förstoring 3/2 ggr ◦ 4:15 vilket innebär en förminskning 15/4 ggr Vanligast är dock att vi har ena siffran 1som i det översta exemplet Det är viktigt att kunna skrivsättet! ◦ Det vill säga, vad betyder: 1:100 respektive 3:1 Kan vi skrivsättet så kan vi lista ut vilken beräkning vi ska göra! ◦ Ställ alltid frågan: ska jag få ett mindre eller större värde? ◦ Mindre – dela med skalan (vi ska göra objektet X ggr mindre) ◦ Större – multiplicera med skalan (vi ska göra objektet Y ggr större) En leksaksbil är gjord i skala 1:100 och är 4,5 cm lång. Hur lång är bilen i verkligheten? Lösning ◦ 1:100 innebär att leksaksbilen är en förminskning av den riktiga bilen ◦ Alltså är leksaksbilen 100 ggr mindre än den riktiga bilen ◦ Alltså är den riktiga bilen 100 ggr större än leksaksbilen ◦ Svar: 4,5𝑐𝑚 ∙ 100 = 450𝑐𝑚 = 4,5𝑚 I en bok om insekter finns information om kackerlackor: ◦ ”En kackerlacka kan, beroende på art, vara från några millimeter upp till 12 cm stor” En art är avbildad i skala 5:1 och är på bilden 3 cm stor. Hur stor är denna kackerlacka på riktigt? En annan art är avbildad i skala 1:3 och är även den 3 cm på bilden. Hur stor är denna kackerlacka på riktigt? När vi talar om skala menar vi vanligtvis längdskala ◦ Det vill säga hur många gånger längre/kortare något har blivit Vad får detta för effekt på area respektive volym? Det fungerar på motsvarande sätt för volymer! Skala 1:10 innebär att alla sidor har blivit 10 ggr kortare En kub med sidan 10cm har arean ◦ 10 ∙ 10 ∙ 10 = 1000𝑐𝑚3 En kub med sidan 1cm har arean ◦ 1 ∙ 1 ∙ 1 = 1𝑐𝑚3 Alltså har volymen blivit 1000 gånger mindre ◦ 1000 = 103 Areaskalan = Längdskalan2 Volymskalan = Längdskalan3 Detta känner vi igen från enheterna! Om två objekt har exakt samma form (men inte nödvändigtvis samma längder) säger vi att objekten är likformiga ◦ Objekten kan ses som förstoring/förminskning av varandra ◦ De kan vara speglade eller roterade Två objekt är kongruenta om de har exakt samma form och längd ◦ De kan vara speglade eller roterade SSS: Sida-Sida-Sida ◦ Om två trianglar har tre par av lika långa sidor - då är trianglarna kongruenta SVS: Sida-Vinkel-Sida ◦ Om två trianglar ett par av lika stora vinklar och två par av lika långa till vinkeln intilliggande sidor – då är trianglarna kongruenta VSV: Vinkel-Sida-Vinkel ◦ Om två trianglar har två par av lika stora vinklar och där sidan liggande mellan dessa vinklar är lika lång i båda trianglarna – då är trianglarna kongruenta Om två vinklar i en triangel är lika stora så är triangeln likbent ◦ Blå linjen är en bisektris Samma form, men (eventuellt) olika längd Vi kan räkna som om det vore skala/förhållande! ◦ (Det är ju faktiskt det) Exempel s. 38-42 i Bråting, Sollervall, Stadler