Genomgång 11 Likformighet skala
advertisement

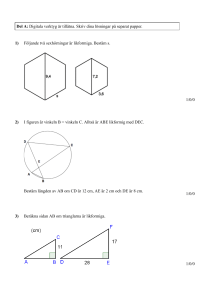
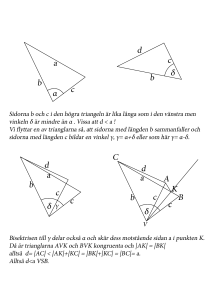
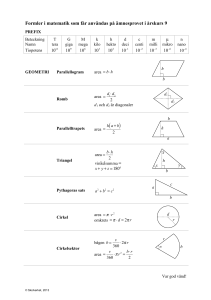
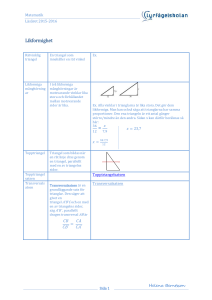
Genomgång 11 Likformighet skala Skala Skalan kan anges på många olika sätt, det vanligaste är t.ex 1:10 000 eller 5:1. Det första innebär en förminskning med 10 000 ggr och det andra en förstoring med 5 ggr. Kom dock ihåg att skala på exempelvis en karta är längdskala vilket inte innebär att arean ökar med denna skala utan med skalan i kvadrat. Enhetsbyten blir nödvändiga att behärska, t.ex. 12 dm2=1200 cm2. Likformiga trianglar Om två trianglar är likadana sånär som på skalan så kallas trianglarna för likformiga och förhållandet mellan likbelägna sidor i de olika trianglarna är lika. Ex. 8 8 6 6 x 6 12 x 9 8 12 8 12 x För att kunna säga att två trianglar är likformiga räcker det att se att trianglarna har två vinklar som är lika stora. Den tredje blir automatiskt lika då summan av vinklarna är 180 Exempel En karta är ritad i skala 1: 100 000. Hur långt är 2 cm på kartan i verkligheten? 2 cm på kartan är 2 100 000 = 200 000 cm = 2 000 m = 2 km i verkligheten. Beräkna sidan markerad med ett x. (trianglarna är likformiga!) 14 10 6 x 8 Likformighet betyder att de är lika men i olika skala! Dvs förhållandet mellan sidorna är lika. Den stora triangeln är 1,4 ggr större (14/10) varför x = 1,4 · 6 = 8,4. 14 x 14 x 6 8,4 Bäst är att direkt ställa upp 10 6 10 1 Trianglar med lika stora vinklar är likformiga I dessa trianglar är kvoten mellan två sidor i den ena triangeln lika stor som kvoten mellan motsvarande sidor i den andra. Exempelvis har vi att När kvoten mellan alla motsvarande sidor är lika säger man att trianglarna är likformiga. Hur stor denna kvot är beror på vinklarnas storlek. Exempel Trianglarna till höger är likformiga. Bestäm sidorna x och y. Lösning: Trianglarna är likformiga. Det innebär att förhållandet mellan motsvarande sidor är lika. Vi får för x: Multiplicera båda leden med 11 Förkorta och räkna ut x = 22 På samma sätt får vi med y Multiplicera med 24 2 Efter förkortning y = 12 Svar: x = 22 cm och y = 12 cm Likformighet, längdskala , areaskala och volymskala Två figurer är likformiga om den ena figuren är en förminskning (eller förstoring) av den andra (och naturligtvis också om de är ”likadana”). Den figur som avbildas kallas vanligen Föremålet. Resultatet kallas då Bilden. Exempel Föremål Bild Graden av förminskning (eller förstoring) uttrycks i ett bråk som kallas skala och som har tecknet : (kolon) i stället för det vanliga bråkstrecket (– eller /). 1:10 (ett på tio), 4:1 (fyra på ett), 1:1 (ett på ett). Är nämnaren större än täljaren är Bilden en förminskning. Är nämnaren mindre än täljaren är Bilden en förstoring. Är både täljare och nämnare 1 är Bilden i ”naturlig storlek”, dvs. lika stor som Föremålet; Bilden är kongruent med Föremålet. En skala kan vara en längdskala, en areaskala eller en volymskala. Längdskala Skalan på en viss karta är 1:100 000 (ett på hundratusen). Det betyder t.ex. att 1 cm på kartan svarar mot ett avstånd i verkligheten som är 100 000 gånger större, dvs. 100 000·1 cm = 100 000 cm = 1 000 m = 1 km 3 Exempel Sidan i en triangel är 6 cm. Hur lång blir sidan i en bild om den avbildas i skalan. a/ 1:6 b/ 4:1 c/ 25 % Lösning: Skalan 1:6 betyder förminskning med 6 gånger. Sträckan blir 6 cm / 6 = 1 a/ cm b/ Skalan 4:1 betyder förstoring 4 gånger. Sträckan blir 6 cm × 4 = 24 cm c/ Skalan 25 % = 0,25 betyder förminskning 4 gånger. Sträckan blir: 6 cm / 4 = 1,5 cm Svar: a/ 1 cm b/ 24 cm c/ 1,5 cm Areaskala En areaskala är längdskalan gånger längdskalan, dvs. längdskalan i kvadrat. Exempel Föremål Bild Längdskalan 1:2 (ett på två) innebär att varje sträcka i Bilden är hälften så lång som motsvarande sträcka i Föremålet. Areaskalan är längdskalan 1:2 i kvadrat, dvs. (1:2)2 = (1:2)·(1:2) = 1/2 · 1/2 = 1/4 = 1:4 (ett på fyra) Det innebär att arean (ytan) av Bilden är en fjärdedel av arean av Föremålet. 4 Volymskala En volymskala är längdskalan gånger längdskalan gånger längdskalan, dvs. längdskalan i kub Exempel Föremål Bild Längdskalan 3:1 innebär att varje sträcka i Bilden är tre gånger så lång som motsvarande sträcka i Föremålet. Volymskalan är längdskalan i kub, dvs. (3:1)3 = (3:1)·(3:1)·(3:1) = 3/1 · 3/1 · 3/1 = 27:1 Bildens volym är alltså 27 gånger så stor som Föremålets volym. 5