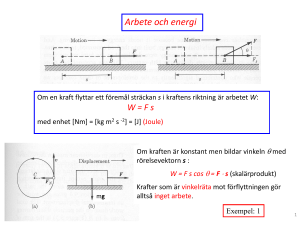
Kurs 5

GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
FY5 Rotation och gravitation
1
3.9.06
MÅL
Kursens mål är att de studerande skall
• fördjupa sitt kunnande i mekanik och sin förmåga att numeriskt kalkylera med fenomen
som sammanhänger med statik och rotation
• fördjupa sina kunskaper om den mekaniska världsbilden.
CENTRALT INNEHÅLL
• kraftmoment och rotationsjämvikt
• modeller för rotationsrörelse, likformig och likformigt accelererad rotationsrörelse
• ekvationen för rotationsrörelse
• rörelsemängdsmomentets konstans
• rotationsrörelsens energi
• cirkelrörelse och dess acceleration
• gravitation och rörelser som påverkas av gravitation
• kaströrelser och planeternas rörelser
• satelliter och deras användning
5.1. Repetition: likformig (LR) och likformigt accelererad rörelse (LAR)
Likformig rörelse, dvs. rörelse med konstant hastighet följer
s = vt
M111
Likformigt accelererad rörelse, med sträckan s = x följer följande formler: Enligt
definitionen på acceleration som förändring i hastighet per den tid förändringen tog fås
a = (v - v0) / t
M111
v = v0 +at
M111
vm = (v0 + v)/2
M111
vilket kan omformas till att
LAR I
Då för medelhastigheten gäller
och sträckan s = x = vmt fås även
LAR II
x = (v0 + v)t/2
M-
Vi kan även visa att
LAR III
x = v0t + ½at2
M111
samt
LAR IV
v2 = v02 + 2ax
M-
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
2
5.2 Kaströrelse = projektilrörelse (FY4 s. 68 - 78)
Denna rörelse är en samtidig LR horisontellt och LAR vertikalt. Dessa rörelser behandlas
var för sig med ovan nämnda formler. Tiden t för en viss händelse (hela kaströrelsen, för
att nå den högsta punkten eller annat) är en variabel som kan användas för att koppla ihop
de två typerna av rörelse.
I bilden ovan har vi u = v0 och vinkeln upp från horisonten α0 = θ. Vi får
horisontellt:
v0h = v0cos α0 där det gäller att
 sh = xh = v0ht = vht
vertikalt:
v0v = v0sin α0 samt av = g = - 9.81 m/s2 där det gäller att
 vv = v0v +avt
 vmv = (v0v + vv)/2
 sv = xv = v0vt + ½avt2
 vv2 = v0v2 + 2avxv
Rörelsen har samma form som en upp- och nedvänd parabel: Om vi gör en graf med xh
på vågrät axel ("vanlig x-axel") fås där xh = vht => t = xh/vh dvs om vh = 1 m/s samma
värden som tidsvärdena; om vh är något annat vilket kan kompensera med annan
skalindelning.
Om vi sätter xv = v0vt + ½avt2 på lodrät axel ("y-axel") är detta en andragradsfunktion av
variabeln på x-axeln med en negativ koefficient för andragradstermen (då x v valts positiv
uppåt blir av = - 9.81 m/s2.
För hela kaströrelsen fås följande figur:
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
3
Vid nedslaget får vi ofta en ny vinkel ned från horisonten, θ' = α. För denna gäller

tan α = vv/vh => α = arctan(vv/vh)
eller motsvarande med sin- eller cos-funktioner med hjälp av sluthastigheten v där vi
enligt Pytagoras har

v2 = vv2 + vh2
Specialfall 1
Vi studerar endast rörelsen upp till kastbanans högsta punkt. Då är vv = 0 och t = stigtiden
och xv = stighöjden h. Jfr s. FY5 s.74. Vi får då:

vv = v0v +avt = avt så stigtiden t = - v0v/av = - v0sinα0/av

vv2 = v0v2 + 2avxv ger stighöjden xv = -v0v2/2av = -(v0sinα0)2/2av
Specialfall 2
Vi studerar kaströrelse som börjar och slutar på samma nivå. Då är xv = 0, ofta kallas xh =
kastvidden = R (eng. 'range'). Tiden kan kallas flygtid, T. Vi får nu:




xv = v0vt + ½avt2 = 0 vilket ger t(v0v + ½avt) = 0 med triviallösningen t = 0
samt (v0v + ½avt) = 0 vilket ger t = - 2v0v/av = - 2v0sinα0/av = flygtiden T (=
dubbla stigtiden)
och kastvidden xh = v0ht = v0cos α0t där flygtiden insätts och ger
xh = (v0cos α0)(- 2v0sinα0/av) = - (2v02/av)sinα0cosα0
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
4
Detta kan med hjälp av den trigonometriska identiteten 2sinαcosα = sin(2α) även skrivas
som
 xh = -(2v02/av)sin(2α0)
Då maximala värdet för en sinusfunktion fås för vinkeln 90o har vi här att största kastvidd
teoretisk uppnås då 2α0= 90o eller α0 = 45o.
5.3. Likformig cirkelrörelse (FY4 s. 26-31)
Då ett föremål rör sig i en cirkel med radien r med konstant fart (hastighetens storlek)
påverkas det av en centripetal kraft Fc riktad inåt mot cirkelns centrum. P.g.a.
Newtons III påverkas det som ger upphov till den centripetala kraften av en lika stor kraft
åt motsatt håll. På det som rör sig i en cirkel verkar dock ingen "centrifugal" kraft. Den
centripetala kraften utgörs i olika situationer av olika krafter:





planet runt sol eller måne runt planet: gravitationskraft
boll som svingas i snöre : spännkraften (force of tension) i snöret
bil som svänger i en kurva : vilofriktion mellan däck och vägyta
kläder i tvättmaskin: normalkraft från tvättmaskinens trumma
laddad partikel i magnetfält: magnetisk kraft
Om föremålet i cirkelrörelse har massan m gäller
Fc = mac
där ac = centripetal acceleration, även kallad normal acceleration an då den är i rät vinkel
till hastighetens riktning. Man kan härleda en formel för den centripetala accelerationen
enligt följande:
Låt en triangel bildas av vektorn v, förändringen i hastighet under en kort tid t dvs.
vektorn Δv och den nya hastighetsvektorn v + Δv transporterad så att den börjar i samma
punkt som v. Då hastighetens belopp är konstant även om riktningen ändras är detta en
liksidig triangel där vinkeln mellan vektorerna v och v + Δv är lika stor som den vinkel
cirkelns radie r förflyttats under denna tid t eftersom både v och v + Δv är i rät vinkel till
radien. En liksidig triangel med spetsen i cirkelns centrum fås, där två sidor lika med
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
5
radien och den tredje en korda i cirkeln som då den valda tiden t är kort är ungefär lika
lång som den sträcka s föremålet i cirkelrörelse rört sig längs cirkelbågen. Denna triangel
är likformig med den förstnämnda (båda är liksidiga, vinkeln mellan de lika sidorna är
densamma) varför förhållandet mellan motsvarande sidor är detsamma:



Δv/v = s/r där ungefärligen s = vt så att
Δv/v = vt/r vilket ger
Δv/t = v2/r = accelerationen
an = v2/r
M111
vilket om ingen annan acceleration är nämnvärd kan skrivas som
Fc = mv2/r
M-
Då den konstanta hastigheten (till sin storlek) är
 v = s / t och
 s = 2πr får vi om tidsperioden för ett omlopp t = T att
 ac = v2/r = (2πr)2/r = 4π2r/T2
eller
Fc = 4π2r/T2
Cirkelrörelsen som kaströrelse
Cirkelrörelsen kan även ses som ett specialfall av kaströrelse i parabolbana. Tag som
exempel en vertikal cirkel vars högsta punkt är A, från vilken ett föremål rör sig längs
cirkeln till punkten B som är något lägre. Om vi omtolkar denna bana som en kastbana är
hastighetens storlek v i cirkelrörelsen här en horisontell utgångshastighet v0 = v0h och den
sträcka s föremålet rör sig längs cirkeln ungefär s = sh = v0ht = vt.
Samtidigt faller dock föremålet på grund av tyngdaccelerationen g = av en sträcka sv =
v0vt + ½avt2 = ½avt2. Låt nu cirkelns radie vara r, dvs sträckan från cirkelns centrum O till
A men även från centrum till B. Bilda en triangel med hypotenusan OB, en katet vertikal
från O till en punkt C under A på avståndet r - sv från O, och en katet horisontell från C
till B. Den sistnämnda kateten = sh. Pytagoras' sats ger då:







(OB)2 = (OC)2 + (CB)2 eller
r2 = (r - sv)2 + sh2 vilket ger r2 = r2 - 2rsv + sv2 + sh2 så
sh2 = 2rsv - sv2 där vi antar att vi valt en mycket liten del av
cirkelrörelsen/kaströrelsen, så att sv << 1 och sv2 = ungefär 0, vilket ger:
sh2 = 2rsv vilket ger sv = sh2/2r men då enligt tidigare sh = vt även
sv = (vt)2/2r i vilket nu insätts sv = ½avt2 så vi får
½avt2 = ½v2t2/r och efter förenkling
av = v2/r
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
6
Om vi som antaget studerat endast en liten del av cirkelrörelsen är tyngdaccelerationen
ungefär riktat mot cirkelns centrum, och fungerar som centripetalacceleration i
motsvarande cirkelrörelse, varför detta är ett alternativt sätt att härled acentripetal = v2/r.
Vi återkommer senare till "accelererad" cirkelrörelse, dvs rörelse där hastighetens belopp
v ändras och föremålet börjar rotera snabbare eller långsammare kring cirkelns centrum.
Kurvtagning I : Plan kurva
Vilofriktionskraften i sidled mellan däck och vägyta fungerar som centripetal kraft. För
att beräkna den hastighet med vilken man kan ta en kurva där friktionskoefficienten är μ
fås, med r = kurvans radie och m = bilens massa:
μmg = mv2/r => v = √(μgr)
Kurvtagning II : Doserad kurva utan friktion
Kurvan är doserad, dvs. lutar i vinkeln α från horisontell riktning. Om ingen friktion finns
eller behövs kan vi beräkna den hastighet kurvan kan tas med även om den är täckt av
glashal is. Normalkraften FN = N delas upp i en lodrät komponent som balanserar
tyngdkraften mg och en vågrät komponent som fungerar som centripetal kraft. Vi får att
Vertikalt: mg = Ncosα
Horisontellt: mv2/r = Nsinα
Division av ekvationerna ger
(mv2/r)/(mg) = Nsinα/ Ncosα = tanα
=> v = √(grtanα) eller α = arctan(v2/gr)
Kurvtagning III : Doserad kurva med friktion
Om vi betraktar gränsfallet där vi söker maximal hastighet v som kurvan kan tas med har
vi en vilofriktionskraft längs vägytan "inåt och nedåt" i kurvan. Vertikalt balanserar en
uppåtriktad komponent av normalkraften N ut tyngdkraften och en nedåtriktad
komponent av friktionskraften. Centripetalkraften utgörs av summan av normalkraftens
och friktionskraftens horisontella komponenter:
Vertikalt: mg + μNsinα = Ncosα => mg = Ncosα - μNsinα
Horisontellt: mv2/r = Nsinα + μNcosα
Division av ekvationerna ger
(mv2/r)/(mg) = (Nsinα + μNcosα)/(Ncosα - μNsinα)
v2/gr = (sinα + μcosα)/(cosα - μsinα)
; förkorta med N i höger led
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
7
Detta ger v = √[gr(sinα + μcosα)/(cosα - μsinα)] = √[grtanα] om μ = 0. Om α = 0 varvid
sinα = 0 och cosα = 1 får vi v = √[μgr]. För att få reda på α tar vi istället korsvis
multiplikation:
v2(cosα - μsinα) = gr(sinα + μcosα)
; distribuera i parenteserna
v2cosα - v2μsinα = grsinα + μgrcosα
; cos-termer till vänster,sin->höger
2
2
v cosα - μgrcosα = grsinα + v μsinα
; faktorisera ut sin och cos
cosα(v2 - μgr) = sinα(gr + v2μ)
; dividera med cosα(gr + v2μ)
tanα = (v2 - μgr)/ (gr + v2μ)
α = arctan[(v2 - μgr)/ (gr + v2μ)] = arctan[v2/gr] om μ = 0.
5.4. Universell gravitation (FY4 s. 57-60)
Cavendish's experiment i slutet av 1700-talet mätte tyngdkraften mellan metallklot på en
horisontell stång upphängd i en tråd. Den mycket svaga kraften vrider tråden en aning,
och genom att låta ljus reflekteras från en spegel på tråden till en skala en bit längre bort
kan mycket små vridningar mätas. Resultatet är en bekräftelse av den allmänna
gravitationslagen som Newton formulerat redan tidigare på basen av planeternas rörelser:
F = m1m2/r2
M112
där m1 och m2 är två massor, r är avståndet mellan dem om de är punktformiga, eller
mellan deras mittpunkter om de är sfärer, och  (MAOL) eller f (FY4-boken) eller G (IB)
är den universella gravitationskonstanten = 6.67 * 1011 Nm2kg-2.
Figur av två sfäriska objekt
5.5. Gravitationsfältstyrka, potentiell energi och potential (FY4 s. 61-63)
Då tyngdkraften blir svagare längre bort från en kropp, t.ex. planeten Jorden, påverkas
även tyngaccelerationen. Denna beskriver en egenskap hos rummet omkring en massa,
och kan även kallas gravitationens fältstyrka.
F = mg ger g = F/m där m = massan av en satellit e.dyl. som påverkas av jordens
tyngdkraftsfält. Det skulle vara bra att skilja mellan detta och massan av den planet eller
annat som förorsakar fältet, exempelvis genom att använda symbolerna m och M.
g = M/r2
M-
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
8
Fältstyrkan (tyngdaccelerationen) g är en storhet som beskriver en egenskap hos rummet i
en viss punkt - om en hypotetisk testmassa mtest placerades i denna punkt, skulle den
påverkas av kraften F = mtestg. Fältet kan (liksom elektriska fält) åskådliggöras med
fältlinjer vilka omkring en planet är riktade in mot dess centrum.
Då en kraft F förflyttar en kropp en sträcka s är det arbete som utförs W = Fs om kraften
är konstant. Om kraften varierar med sträckan är arbetet W = arean under en graf av F
som funktion av s. Exempelvis för harmonisk kraft F = (-)kx fås det arbete som utförs då
en fjäder töjs ut ur figuren nedan; detta arbete lagras som elastisk potentiell energi i den
uttöjda fjädern.
Då man lyfter upp ett föremål i rymden från en planetyta förändras kraften då avståndet
till planetens centrum förändras märkbart. Genom integralkalkyl kan man visa att det
arbete som utförs och därmed den potentiella energi som lagras följer formeln:
Ep = -m1m2/r
M112
där minustecknet anger att föremålet fortfarande är bundet till planeten. Nollnivån för
potentiell energi kan väljas fritt, här är den oändligheten.
Tyngdkraftspotentialen definieras som V = Ep/mtest, vilket ger V = Ep = (-m1m2/r)/m2
eller med planetens massa m1 = m följande:
V = -m/r2
M-
Om planetens (eller en annan verkligen existerande) massa symboliseras med M och den
hypotetiska testmassan med m fås följande sammafattning:
Storhet
kraft
fält (=acceler.)
potentiell energi
potential
Vid jordytan
F = mg
g = F/m
Ep = mgh
V = Ep/m = gh
Universellt
F = Mm/r2
g = M/r2
Ep = -Mm/r
V = -M/r
Enhet
N
Nkg-1 (=ms-2)
J
Jkg-1
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
9
Tyngdkraftspotentialen är en mer sällan använd storhet, men då inom elläran dessa
formler har mycket likartade motsvarigheter (med elektrisk laddning i stället för massa)
kommer då elektrisk potential och speciellt potentialskillnad = spänning att vara en ofta
använd storhet).
5.6. Satelliter och tyngdlöshet
Med den universella formeln för potentiell energi i ett tyngdkraftsfält ovan kan man
beräkna det arbete som krävs för att lyfta en satellit till en viss höjd över jordens yta. Men
om satelliten endast lämnas där faller den snart ned igen (vilket är fallet för s.k.
"rymdfärder" i ballistisk bana, där en nästan lodrät kaströrelse genomgås). För att få en
satellit att stanna ute i rymden en längre tid måste den placeras i en stabil omloppsbana
kring jorden.
I en sådan omloppsbana kommer besättningen på en rymdfarkost att uppleva tyngdlöshet
- men detta beror inte på att de är så långt ute i rymden att tyngdkraften försvunnit; i en
typisk satellitbana några hundra km ovanför jordytan har avståndet till jordens centrum
inte förändrats radikalt. I stället är i en stabil omloppsbana tyngdkraften i funktion
som centripetal kraft för den cirkelrörelse det gäller. (Man kan även beskriva
situationen som ett "fritt fall", där rymdskeppet hela tiden faller med den
tyngdacceleration som gäller på det valda avståndet från jorden - men där denna
acceleration fungerar som centripetal acceleration. Då en analogi mellan kaströrelse och
cirkelrörelse enligt tidigare kan göras, kan man även säga att det är en kaströrelse där
jordens yta böjer sig undan "projektilen" så att dess höjd över den förblir konstant).
För att få reda på den kinetiska energi som satelliten bör ha (förutom den rätta potentiella
energin) utgår vi från


Fc = Fg vilket ger = Mm/r2 = mv2/r och sedan
mv2 = Mm/r och sedan ½mv2 = Mm/2r
Den totala energin för en satellit i stabil omloppsbana blir alltså

Etot = Ep + Ek = - Mm/r + Mm/2r = - Mm/2r
Sammanfattning för energier i stabil omloppsbana:
Ep = - Mm/r
vilket visas i grafen nedan:
Ek = Mm/2r
Etot= - Mm/2r
M-
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
10
Den hastighet en satellit eller ett rymdskepp i en stabil omloppsbana har fås enligt


½mv2 = Mm/2r vilket ger
v2 = M/r
dvs. att banhastigheten på avståndet r från centrum av en planet med massan M är
vban = (M/r)
M-
För att helt bryta sig fri från en planets gravitationsfält bör en rymdfarkost (minst)
komma upp till en total mekaniska energi som är noll; är denna negativ är farkosten ännu
bunden till planeten:



Ep + Ek = 0 ger - Mm/r + ½mv2 = 0 och därmed
- 2M/r + v2 = 0 och sedan
v2 = 2M/r
varför flykthastigheten från planetens yta blir
vflykt = (2M/r) = vban2
M-
Detta är en hastighet sådan att om en farkost på planetens yta gess denna
begynnelsehastighet kommer den aldrig att återvända till planeten eller röra sig i någon
omloppsbana runt den, utan i oändlighet avlägsna sig.
Detta under antagande att atmosfärens luftmotstånd inte inverkar, och att farkosten inte
har någon kinetisk energi i början. Det är inte helt sant då även ett rymdskepp som står
"stilla" på jordens yta rör sig runt jordaxeln en gång per dygn. Den utgångshastighet
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
11
farkosten därmed har är större ju närmare ekvatorn uppskjutningsplatsen finns, och
förutsätter att farkosten skjuts iväg åt öster. Då man därtill önskar att den första delen av
en rymdrakets bana går över hav så att skadorna minimeras om den exploderar vid
uppskjutningen är det gynnsamt att välja en startplats på en östkust så nära ekvatorn som
möjligt (Florida i USA, Franska Guayana för EU).
5.7. Planeternas rörelser: Keplers lagar
Man kan visa att det av den universella formeln för tyngdkraft följer att planeterna i sin
rörelse runt solen (eller flere månar/satelliter i rörelse runt samma planet) följer dessa
lagar:
Keplers I. lag: Planeterna rör sig i en ellips med solen i ena brännpunkten
En ellips är en "uttänjd cirkel" som kan ritas om två häftstift sätts i ett papper och ett
snöre något löst runt dem; snöret spänns med spetsen av en penna och ellipsen
uppkommer då man för runt pennan med snöret spänt. Stiften utgör "brännpunkter"; ju
närmare varandra de är desto mer liknar ellipsen en cirkel. Ju längre i från varandra de är,
desto mer "excentrisk" är ellipsen.
Keplers II. lag : En linje från solen till en planet sveper över samma yta under samma
tid.
Detta innebär att planeten rör sig snabbast nära solen och långsammare längre bort.
Keplers III. lag: Planeterna rör sig i ellipser som ungefär är cirklar sådana att
omloppstidens (T) kvadrat är proportionell mot banradiens (r) kub.
Detta kan visas enligt följande (M = solens massa, m = planetens)




Fc = Fg ger som vanligt Mm/r2 = mv2/r och med v = 2r/T fås
M/r2 = v2/r vilket ger M/r2 = (2r/T )2/r så
M /r2 = (42r2/T2)/r = 42r/T2 vilket sedan ger
T2 = 42r3/M = kr3 där konstanten k är densamma för alla kroppar i stabil
omloppsbana kring den centrala massan M.
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
12
5.8. Kraftmoment, rotationsjämvikt och statik (FY4 s. 35-46)
Om du med en hand bär en bricka med en tung tallrik på är det lättare att hålla den vågrät
om tallriken är nära den bärande handen. Ändå är tyngdkraften på tallriken lika stor
oberoende av var på brickan den placeras. För att beskriva krafters inverkan på
"vridande" eller roterande rörelse behövs en ny storhet:
När en kraft F verkar på avståndet r från en punkt P definieras kraftmomentet (tidigare
vridmomentet, eng. "torque" eller ibland "moment", inte att förväxla med eng.
"momentum" = rörelsemängd) M enligt
M = Fr
M113
Om vinkeln θ mellan kraften och en linje från kraftens angreppspunkt A till P inte är rät,
räknas endast den komponent av F som är vinkelrät mot AP (eller den komponent av AP
som är vinkelrät mot F) vilket ger att i det allmänna fallet
M = Frsinθ
Enheten för kraftmoment är 1 Nm, men till skillnad från situationen för arbetet W = Fs är
denna enhet inte detsamma som 1 joule. Arbetet är en skalär storhet, medan
kraftmomentet är en vektorstorhet som kan ha riktningarna medurs eller moturs.
(Matematiskt är W = F • s medan M = r X F, skalär produkt respektive vektorprodukt).
Den punkt P som används för att beräkna M kallas ibland stödjepunkt e.dyl., eng. "pivot",
och kan ofta i problemlösning vara en punkt omkring vilken något kan tänkas rotera, t.ex.
gångjärnet i en dörr eller något föremåls upphängninspunkt. Det bör dock egentligen
betraktas som ett matematiskt verktyg liknande axlarna i ett valt koordinatsystem.
För krafter kan vi definiera translatorisk jämvikt som en situation då summan av alla
krafter (med relevanta tecken, om en riktning är positiv är motsatt riktning negativ) är
noll i vilken vald dimension som helst (upp/ner, framåt/bakåt, uppför en backe/nedför en
backe e.dyl, vinkelrätt in i/ut ur ett plan etc). Om en sådan translatorisk jämvikt råder
kommer föremålet att förbli i vila eller rörelse med konstant hastighet till både storlek
och riktning ( = Newtons I. lag).
För kraftmoment definieras rotationsjämvikt som en situation då summan av alla
kraftmoment (med olika tecken medurs och moturs) är noll räknat med avseende på
vilken pivot-punkt som helst. Om en sådan rotationsjämvikt råder kommer föremålet att
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
13
förbli i vila (rotationsmässigt) eller i rotation med konstant rotationshastighet (till storlek
och rotationsriktning, medurs/moturs).
Notera att translatorisk rörelse och rotationsrörelse kan behandlas oberoende av varandra;
ett föremål kan röra sig translatoriskt utan rotation (en kälke som glider nerför en backe),
endast rotera (propellern i ett vindkraftverk), eller ha båda rörelserna samtidigt (en
gevärskula som roterar medan den rör sig framåt). En planets rörelse runt solen kan å ena
sidan beskrivas som tranlatorisk rörelse där hastighetens riktning hela tiden ändras av
centripetalaccelerationen, å andra sidan som rotationsrörelse utan något kraftmoment
medurs eller moturs (tyngdkraften är hela tiden i samma riktning som en linje mellan
planeten den verkar på och solen i pivotpunkten, varför vinkeln θ = 0o och därmed M = 0.
Statik - kroppar i vila
Ett specialområde av mekaniken är statiken, som behandlar fall där varken rotations- eller
translationsrörelse förekommer. Denna är tillämpbar inom arkitekturen för de fall där
man inte vill att byggnader eller andra konstruktioner skall röra sig på något sätt. Vid
problemlösning kan både kravet på translatorisk- och rotationsjämvikt utnyttjas för att
ställa upp ekvationer - varvid vilka dimensioner som helst kan användas för translatorisk
jämvikt (vanligen upp/ned, höger/vänster) och rotationsjämvikt (vanligen föremåls mitteller ändpunkter). Notera att man kan eliminera kraftmomentet från en okänd kraft
genom placera pivotpunkten i dess angreppspunkt (r = 0 ger M = 0) eller i kraftens
riktning förlängd framåt eller bakåt (θ = 0o ger M = 0).
5.9. Massmedelpunkt och tyngdpunkt (FY4 s. 47-53)
Tyngdkraften FG kan för "regelbundet" formade kroppar antas verka i deras geometriska
mittpunkt, t.ex. i mitten av en stav om den är homogen. För ett gungbräde upphängt i sin
mittpunkt (vänster figur nedan) behöver alltså endast övriga krafter (tyngkrafterna på
barnen som sitter på brädet) beaktas då pivotpunkt placeras i brädets mittpunkt.
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
14
För geometriskt mer oregelbundna kroppar kan man finna massmedelpunkten genom att
indela den i mindre delar vars massmedelpunkter är geometriskt uppenbara (i princip kan
man fortsätta indelningen tills delarna är enskilda atomer) och låta dessa delars
massmedelpunkter m1, m2, m3, .... beskrivas av koordinaterna (x1,y1), (x2,y2), (x3,y3), .... i
ett valt koordinatsystem. Massmedelpunktens läge i detta system är då i x-led
xmmp = (m1x1 + m2x2 + m3x3 + .....)/mtot
där mtot = m1 + m2 + m3 + .... och i y-led fås
ymmp = (m1y1 + m2y2 + m3y3 + ....)/mtot
I de fall där kroppen kan tänkas bildas genom att någon del tas bort från en enklare kropp
(ex. ett cirkelrunt hål någonstans i en fyrkantig platta, eller tvärtom) kan den bortagna
kroppens massa och tyngdpunktskoordinater användas med negativt förtecken. Om
kroppen är i ett homogent tyngdkraftsfält (vilket i regel är fallet, om kroppens
dimensioner är små i förhållande till den planet som huvudsakligen förorsakar fältet) är
denna massmedelpunkt (center of mass) lika med dess tyngdpunkt (center of gravity).
Komplikationer kan närmast förekomma i astronomiska sammanhang där
tidvatteneffekten beror på att de delar av jorden som är längst bort från månen påverkas
av en svagare tyngdkraft än de som är närmast.
5.9. Från translations- till rotationsrörelse (FY4 s. 79-99)
Då en kropp rör sig i en cirkel med radien r kan den vinkel cirkelns radie svept över
anges antingen i enheten grader eller i radianer, definierade så att
x = b/r
M32
där x är vinkeln, b = längden av den cirkelbåge kroppen följt. Då ett helt varv innebär b =
2πr = 360o fås sambandet
π rad = 180o
M32
eller 1 radian = 1 rad = (180/π)o = ca 57o. Inom fysiken kallas detta vridningsvinkeln
eller vinkelförskjutningen (angle, angular displacement)  vilket då båglängden, den
sträcka längs cirkelbågen kroppen rört sig betecknas s gör att x = b/r blir  = s/r eller
s = r
M111
Ofta betecknas vridningsvinkeln som positiv moturs och negativ medurs (jfr
trigonometrisk enhetscirkel).
Då kroppen i cirkelrörelse vrider sig en vinkel  eller Δ på tiden t eller Δt blir dess
vinkelhastighet
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
Δ = Δ / Δt
15
M111
eller
=/t
i enheten rad/s. Om vi låter v = s / t = beloppet av den hastighet (med hela tiden
föränderlig riktning) kroppen rör sig längs cirkeln med fås
 s = r => v = s/t = r/t = r
Rotationshastigheten kan även beskrivas med varvtalet n = 1/T, där T = tiden för ett varv.
Då ett varv är 2π radianer blir motsvarande vinkelhastighet 2π/T = 2πn.
v = r
M111
Om hastighetens belopp v förändras med tiden har vi en tangentiell acceleration at = Δv/
Δt (till skillnad från den centripetala eller normala accelerationen ac = an = v2/r) kommer
även vinkelhastigheten att förändras vilket beskrivas med en vinkelacceleration  enligt
 = Δ / Δt
där  = Δ/Δt = /t = (v/r)/t = (v/t)/r = at/r vilket ger
at = r
M111
Liksom translatorisk rörelses hastighet förändras av en kraft kommer en rotationsrörelses
vinkelhastighet att förändras av ett kraftmoment M = Fr.
Hur stor acceleration en viss resultantkraft åstadkommer beskrivs för translatorisk rörelse
av Newtons II. lag, F = ma. För att beskriva vilket kraftmoment som behövs för att
åstadkomma en viss vinkelacceleration måste dock massan m ersättas av en storhet kallad
tröghetsmoment J där även massans avstånd till rotationsrörelsens mittpunkt beaktas.
Man kan uppleva detta genom att fatta en golfklubba i fel ända, med den tunga ändan i
handen. Det är nu mycket lättare att svinga den än på normalt sätt då den tunga ändan är
långt från vridningens centrum. Man kan visa att om all massa m är på avståndet m från
rotationscentrum ges tröghetsmomentet (moment of inertia) J av formeln
J = mr2
M113
och har enheten kgm2. Tröghetsmomentet är liksom massan en skalär storhet. För kroppar
som roterar kring en axel så att all massa inte är på avstånde r (som ett ihåligt rör med
tunn vägg) från axeln gäller följande (M113-114):
kompakt cylinder, radie r
kompakt klot, radie r
ihåligt klot, tunn vägg
J = ½mr2
J = (2/5)mr2
J = (2/3)mr2
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
16
stav, längd l, axel i mitten
J = (1/12)ml2
stav, axel i ändpunkt
J = (1/3)ml2
rektangel, sidorna a och b, axel i mittp. J = (1/12)m(a2 + b2)
(Tamburiner konstrueras ibland inte cirkelformiga utan så att rotationsaxeln kommer
närmare mitten för att minska J).
Med hjälp av följande fem storheter kan formlerna för de två typerna av rörelse
"översättas":
Translationsrörelse
Rotationsrörelse
sträckan
hastigheten
accelerat.
kraften
massan
vridningsvinkeln,
vinkelhastigheten
vinkelaccelerationen
kraftmomentet
tröghetsmomentet
s=x
v
a
F
m
=s/r
=v/r
 = at /r
M = Fr (eller Frsinθ)
J = mr2 (e.dyl.)
5.10. Rotationsmekanik
Med hjälp av "ordlistan" ovan fås följande:
Translationsrörelse
Rotationsrörelse
v = v0 + at
x = (v0 + v)t/2
x = v0t + ½at2
v2 = v02 + 2ax
F = ma
p = mv
I = Ft
Ek = ½mv2
 = 0 + t
 = (0 + )t/2
 = 0 + ½t2
2 = 02 + 2
M = J
L = J
I = Mt
Er = ½J2
De fyra första formlerna gäller för likformigt vinkelaccelererad rotationsrörelse, och ges i
M111. Några kommentarer till de övriga:
Mi = Ja(menas J?)
M113
Summan av alla kraftmoment med hänsyn till riktningstecken (medurs/moturs),
resultantkraftmomentet är tröghetsmomentet gånger vinkelaccelerationen. Detta är
rotationsmekanikens motsvarighet till Newtons II. lag. Newtons I lag är ett specialfall av
den II. lagen; och även en motsvarighet till Newtons III lag kan formuleras:
Om A verkar på B med kraftmomentet M, verkar B på A med - M
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
17
Detta innebär t.ex. att om en astronaut på rymdpromenad utanför en rymdstation skall
använda en borrmaskin bör den vara konstruerad så att olika delar av den försätts i rörelse
i motsatt riktning, annars börjar astronauten rotera i motsatt riktning till borrverktyget.
En helikopter måste konstrueras antingen med två rotorer som roterar åt motsatt håll eller
med en extra stjärtrotor som motverkar det kraftmoment -M med vilket huvudrotorn
återverkar på helikoptern.
L = J
M113
Den translatoriska storheten rörelsemängd (momentum) p motsvaras av
rörelsemängdsmomentet (angular momentum, rotational momentum) L i enheten
kgm2rads-1. För detta gäller en konserveringslag på motsvarande sätt:
Om inget yttre kraftmoment verkar på ett system, är det totala rörelsemängdsmomentet
konstant.
Om en roterande kropp förändrar sin form, så att dess tröghetsmoment J ändras, kommer
vinkelhastigheten  samtidigt att ändras så att L förblir konstant. Ett exempel på detta är
att konståkare på skridsko som sträcker sig för att få masspunkterna i sin kropp så nära
rotationsaxeln som möjligt kommer att börja rotera snabbare. Ett annat exempel är att när
en roterande luftmassa rusar in mot ett lågtryck kommer den att rotera snabbare, ibland
med virvelstormar som följd. Man kan pröva på detta genom att sitta på en lättroterande
skrivbordsstol eller pianopall och försätta sig i rotation med benen utsträckta och sedan
dra in dem snabbt.
Rörelsemängdsmomentet antas i Bohrs atommodell (se FY8) ha vissa speciella värden
vilket leder till elektronernas energinivåer i atomen. Då används L = J = mr2(v/r) = mvr.
I = Mt
M113
Kraftens impuls motsvaras nu av kraftmomentets impulsmoment i enheten Nms.
Er = ½J2
M113
Rotationsenergin får enheten kgm2rad2s-2 = kgm2s-2 då radianer är en dimensionslös
enhet. Vidare blir denna enhet Nm = J som för alla energier.
Detta innebär att om kropp roterar så är krävs ett arbete utfört av ett yttre kraftmoment för
att förändra dess rotationsenergi, vilket gör att en cykel är stabilare med snurrande hjul,
och en kula stabilare om den försätts i rotation av räfflor i gevärspipan.
GYMNASIEFYSIKKOMPENDIET 2005: FY5 ROTATION OCH GRAVITATION
18
5.11. Kombinerad translations- och rotationsrörelse
Rullning
Om t.ex. en kompakt cylinder rullar nedför en sluttning kommer dess potentiella energi
att övergå till både translatorisk kinetisk energi och rotationsenergi:
 Ep = Ek + Erot
 mgh = ½mv2+ ½J2 vilket med J = ½mr2 och  = v / r ger
 mgh = ½mv2+ ½½mr2(v/r)2 vilket ger
 mgh = ½mv2+(1/4)mv2 = (3/4)mv2
och så vidare.
Centripetal och tangentiell acceleration
Cirkelrörelse kan beskrivas som en translatorisk rörelse med en acceleration vinkelrätt
mot rörelseriktningen. Om den sedd som rotationsrörelse även uppvisar en ökad
vinkelhastighet har vi både en centripetal (normal) acceleration och tangentiell
acceleration; för dessa gäller att den totala accelerationen är
atot2 = ac2 + at2
5.12. Exempel på laborationer
1. Skjut iväg ett gummiband från en kort linjal e.dyl. och mät hur långt det flyger för
olika vinklar (t.ex. 5ggr var för olika vinklar från 10o till 80o). Gör graf av räckvidd som
funktion av vinkel. Vilken vinkel ger största räckvidden? Vilken vinkel borde teoretiskt
ge största räckvidden; varför är experimentets resultat lite annat? Hur kan man bestämma
utgångshastigheten då gummibandet töjts på ett visst sätt (skjut lodrätt uppåt, sätt mgh =
½mv2).
2. Försätt ett litet föremål i horisontell cirkelrörelse med hjälp av ett snöre, en glatt liten
cylinder och en vikt. Beräkna den centripetala accelerationen utgående från varvtalet och
jämför värdet med viktens tyngd
3. Datorlaboration : Konstruera eller använd och analysera ett kalkylblad som simulerar
landning av en rymdfarkost på månen eller andra himlakroppar. Användaren kan sekund
för sekund välja hur stor kraft från raketen som används, vilket påverkar
bränsleförbrukningen och därmed den totala massan. Tävla om vem som kan "landa"
skeppet snabbast utan att träffa månens yta för snabbt, eller med största mängd bränske
kvar! Studera grafer av höjden, hastigheten och accelerationen och diskutera hur de är
relaterade till varandra. Hur kan bladet utvecklas så att det tar hänsyn till hur
tyngdaccelerationen förändras med avståndet till månen?
4. Konstruera en hemgjord balansvåg av t.ex. en linjal och en känd massa för vägning av
okända. Beräkna mätnoggrannheten och jämför med resultaten från färdiga vågar.