Avkylning ~ T HAV - math.chalmers.se
advertisement

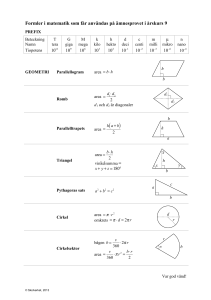
Kan golfströmmen sjunka? Ett exempel på hur man använder matematik i forskning i oceanografi Anna Wåhlin Docent, inst. för Geovetenskaper Oceanografi = havets fysik Vad driver havsströmmarna? Vad skulle kunna få dem att ändra sig (klimat)? Vind, solinstrålning + avkylning, regn, … Vågor, tsunamis, tidvatten Värmetransport i havet (stor värmetransport! 10 m hav = hela atmosfären) Is: Isfrysning, smältning, sönderbrytning av isflak, etc… Ekmanspiralen: Vindens + jordrotationens inverkan på havet Ekmanspiral (matematisk lösning): Strömhastigheten norrut Strömhastighet västerut En produkt av exp- och sinus/cosinus. Används fortfarande för att beräkna vinddriven transport etc i havet. Kan golfströmmen sjunka? Kyls av, regnar Varmt, salt Varmt vatten är lätt, salt vatten är tungt.. Traditionella sättet att tänka på havscirkulationen - Värms vid ekvatorn, kyls vid polerna (ersätter temp- och salt-drivning med tyngden (densiteten) Avkylning From Spall, JPO 2004 Sjunker aldrig i bassängen… Ingen rörelse, mycket kallt vatten Avkylning Sjunker! Pga kolliderar med ’golfströmmen’ Varför sjunker det inte? Avkylning ~ THAV - TATM Värmeflux = C*(THAV – TATM) Varmt hav => Snabb avkylning THAV = TATM => Ingen avkylning Vattnet inne i bassängen rör sig inte och är därför alltid kallast Hur temperaturen ändras: TIN -> TATM, längdskala LT Inflöde (”Skottland”) TIN Utflöde (”Grönland”) TATM LT Avstånd längs kusten (y) LT bestämmer hur snabbt värmen försvinner Salthalt: Färskare vatten pga regn/floder Färskvattenflöde = F Inte beroende av havets salthalt Ingen koppling mellan drivning och salthalt => längre längdskala för salthalt Hur salthalten ändras: SIN -> SEQ Längdskala LF >> LT (för nästan alla hav) SIN SEQ: Regn/floder balanseras genom blandning med det vatten som är i bassängen SEQ Avstånd längs kusten (y) 0 < SEQ < SBASIN LF Densitet = A*Temp + B*Salthalt Avstånd längs kusten Värme och salt kompenserar, men justeras med samma längdskala => golfströmmen kan inte sjunka Sjunker Sjunker Bassängvattnets densitet Avstånd längs kusten Värme och salt kompenserar men på olika längdskala (temperatur snabbare än salt): Avstånd längs kusten Cold and salt compete, and cold is faster => sinking Sjunker Sjunker Bassängvattnets densitet Avstånd längs kusten Kan golfströmmen sjunka? • Måste avkylas snabbare än den blir färskare • Måste kylas av tillräckligt mycket • Måste vara tillräckligt salt • Vad är längdskalorna, vad är jämviktsvärdena för T och S? Förenklad modell! Färskvattentillförsel (F) Värmeutbyte med atmosfären (relaxation) Blandning med bassängen: M (vind, virvlar) Konstant transport strömmen, stillastående vatten i bassängen E.g. Nordic Seas Värmebudget i havsströmmen (förändring av temperatur = det man stoppar in – det man tar ut) Utbyte med bassängen (T ( y ) TINT ) (T ( y ) TAIR ) dT dy LE LA dT Q M (T TINT ) R A (T TAIR ) dy Förändr ing Utbyte med atmosfären Q LE M Bassängens längdskala LA Q R A Atmosfärens längdskala (T ( y ) TINT ) (T ( y ) TAIR ) dT dy LE LA dT dT T ( y) T ( y ) T ( y ) Ce y dy dy T ( y ) (T0 Teq ) e Teq LETAIR LATINT LE LA y LT LT Teq LE LA Q LE LA M R A Lösning: T går exponentiellt från T0 -> Teq, längdskalan LT TEQ T(y) (T0 Teq )e y LT Teq T0 y LT Teq LETAIR LATINT LE LA LT LE LA Q LE LA M R A If RA>>M => LT~LA and Teq~TAIR Styrs av atmosfären If RA<<M => LT~LE and Teq~TINT Styrs av bassängen Saltbudget i strömmen (förändring av salthalt = det man stoppar in – det man tar ut): Salt från bassängen dS Q M ( S S INT ) FS dy Förändring Färskvatten från land dS S ( y ) S INT dy LF LE där Q LF FM och Q LE M Lösning: S går exponentiellt från SIN -> SEQ, längdskalan LS SIN S ( y ) ( S0 S EQ )e y LF S EQ SEQ y LS S EQ S INT 1 LF S INT F LE 1 M LF Q F M Om M<<F => SEQ~0 och LS~Q/F Styrs av regn/floder Om M>>F => SEQ~SINT och LS~Q/M Styrs av bassängen Kan den sjunka? • Första kravet: Lokalt maxima i densitet d 0 dy • Annars ändrar sig densiteten monotont från inflöde mot bassängvattnet Hitta punkten för lokalt maximum, var är derivatan = 0? ( y) S ( y) T ( y) S0 d e dy LS d S0 0 e dy LS y yˆ LS y LS T LT y LS e y LT T LT e (1 ) e 0 T0 E S0 ŷ E y LT S0 LS e y LS T LT LT FM LS R A M e y LT Hitta punkten för lokalt maximum, var är derivatan = 0? e d 0 dy T0 E S0 ŷ (1 ) yˆ YˆCR E där LT FM LS R A M Kvoten mellan temperaturavvikelse och saltavvikelse T0 E S0 LT F M LF R A M E stor => densitetsförändringen temperaturdominerad E liten => densitetsförändringen saltdominerad Kvoten mellan längdskalorna för temperatur och salthalt stor => temperatur långsammare än salt liten => temperatur snabbare än salt För nästan alla havsströmmar: <= 1 Nordiska Hav: E = 1 och = 0.5 Bassängvattnets densitet Andra kravet: Densitetsmaximum måste vara högre än bassängens densitet. Beräkna värdet av densiteten i y = YCR, kolla om det är högre än bassängen Sjunker E = 0.75, olika E = 1.5, olika Golfströmmen kan sjunka om: 1) T är snabbare än S LT 1 LF 2) Tillräckligt varmt och salt vatten i Golfströmmen Lätt bassängvatten Tungt bassängvatten T0 E S0 3) Tillräckligt lätt vatten i Nordiska hav Summering 1. Man måste ta hänsyn till att salt och temperatur justeras på olika längdskalor i havet 2. Havsströmmar kan bara sjunka när T är ’snabbare’ än S ( < 1)… 3. …och strömmen tillräckligt varm/salt (E > ) 4. …och bassängvattnet tillräckligt lätt. 5. Nordiska hav och Golfströmmen är under denna gräns vid våra kuster med dagens klimat. Reference: Wåhlin & Johnson, JPO 2009 (in press)