Kapitel 5.1

Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
Kapitel 5.1
5101, 5102 Exempel som löses i boken
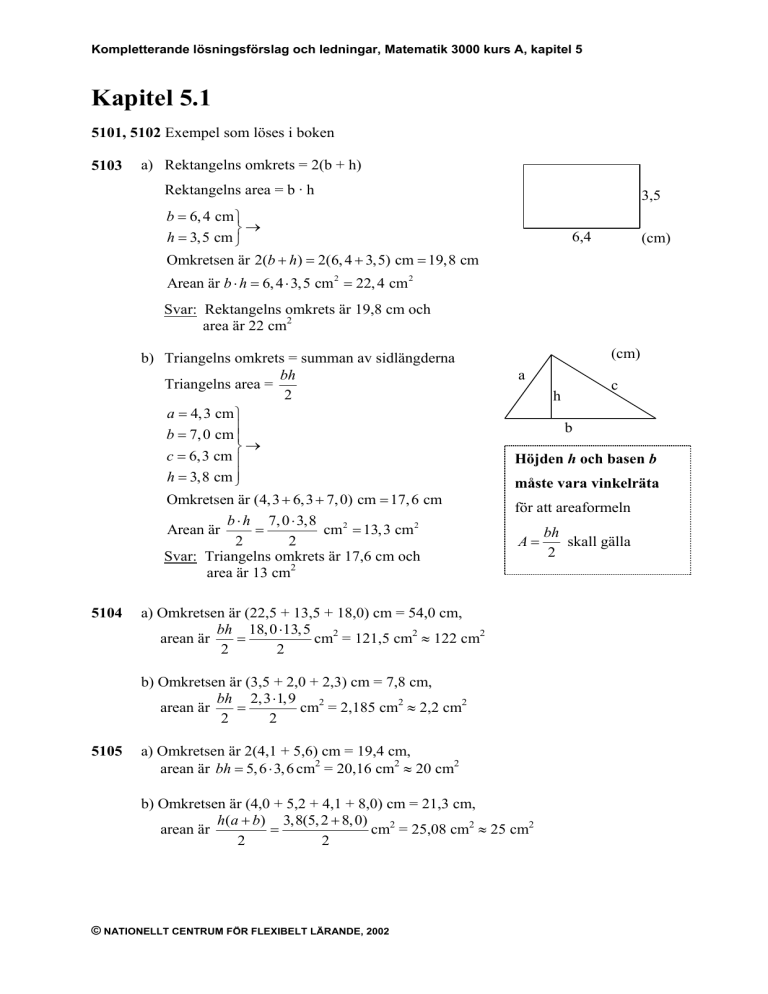
5103
a) Rektangelns omkrets = 2(b + h)
Rektangelns area = b · h
3,5
b = 6, 4 cm 
→
h = 3,5 cm 
Omkretsen är 2(b + h) = 2(6, 4 + 3,5) cm = 19,8 cm
6,4
(cm)
Arean är b ⋅ h = 6, 4 ⋅ 3,5 cm 2 = 22, 4 cm 2
Svar: Rektangelns omkrets är 19,8 cm och
area är 22 cm2
b) Triangelns omkrets = summan av sidlängderna
bh
Triangelns area =
2
a = 4,3 cm 
b = 7, 0 cm 
→
c = 6,3 cm 
h = 3,8 cm 
Omkretsen är (4,3 + 6,3 + 7, 0) cm = 17, 6 cm
b ⋅ h 7, 0 ⋅ 3,8
Arean är
cm 2 = 13,3 cm 2
=
2
2
Svar: Triangelns omkrets är 17,6 cm och
area är 13 cm2
5104
(cm)
a
b
Höjden h och basen b
måste vara vinkelräta
för att areaformeln
A=
a) Omkretsen är (22,5 + 13,5 + 18,0) cm = 54,0 cm,
bh 18, 0 ⋅13,5 2
arean är
=
cm = 121,5 cm2 ≈ 122 cm2
2
2
b) Omkretsen är (3,5 + 2,0 + 2,3) cm = 7,8 cm,
bh 2,3 ⋅1,9 2
=
cm = 2,185 cm2 ≈ 2,2 cm2
arean är
2
2
5105
a) Omkretsen är 2(4,1 + 5,6) cm = 19,4 cm,
arean är bh = 5, 6 ⋅ 3, 6 cm2 = 20,16 cm2 ≈ 20 cm2
b) Omkretsen är (4,0 + 5,2 + 4,1 + 8,0) cm = 21,3 cm,
h(a + b) 3,8(5, 2 + 8, 0) 2
=
cm = 25,08 cm2 ≈ 25 cm2
arean är
2
2
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
c
h
bh
skall gälla
2
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5106
a) Omkretsen är 4 · 1,9 cm = 7,6 cm, arean är 1,9 · 1,9 cm2 = 3,61 cm2 ≈ 3,6 cm2
b) Omkretsen är 2 · (4,8+9,7) cm = 29 cm, arean är 4,8 · 9,7 cm2 = 46,56 cm2 ≈ 47 cm2
5107
a) Omkretsen är (4,3 + 3,4 + 4,9) cm = 12,6 cm,
bh 4,9 ⋅ 2,9 2
arean är
=
cm = 2,755 cm2 ≈ 2,8 cm2
2
2
b) Omkretsen är (3,6 + 7,4 + 5,2) cm = 16,2 cm,
bh 5, 2 ⋅ 3,3 2
=
cm = 8,58 cm2 ≈ 8,6 cm2
arean är
2
2
5108
Omkretsen är 2(3,1 + 5,5) cm = 17,2 cm,
arean är bh = 5,5 ⋅ 2,8 cm2 = 15,4 cm2 ≈ 15 cm2
5109
Omkretsen är (7,1 + 12,0 + 6,4 + 18,0) cm = 43,5 cm,
h(a + b) 6, 0(12, 0 + 18, 0) 2
arean är
=
cm = 90 cm2 ≈ 90 cm2
2
2
5110
Se facit
5111
Se facit. Kontakta din lärare om du vill diskutera din lösning.
5112
Gräsmattan är kvadratisk Æ Alla fyra sidor
är lika långa och alla hörn är vinkelräta.
Omkretsen är 72 m.
Arean är b · b
b
4b = 72 → b = 18
b ⋅ b = 18 ⋅18 = 324 ≈ 320
Svar: Gräsmattans area är 320 m2
b
5113
Beräkna arean för den ”murade” rektangeln och arean av den streckade triangeln
var för sig. Husgavelns totala area är summan av rektangelns area och triangelns area.
Rektangelns area: 8,2 · 3,7 m2 = 30,34 m2
Triangelns area: 1. triangelns höjd h är (7,8 − 3,7) m = 4,1 m
bh 8, 2 ⋅ 4,1 2
2. Arean A =
=
m = 16,81 m2
2
2
Totala arean: 30,34 m2 + 16,81 m2 = 47,15 m2 ≈ 47 m2.
Svar: Husgavelns area är 47 m2
5114
Tak: 2 ⋅1,9 ⋅ 3, 2 m 2 = 12,16 m 2
Sidor: 2 ⋅ 3, 2 ⋅ 0,8 m 2 = 5,12 m 2
2 ⋅ 3, 2 ⋅1,1 2
m = 8,64 m2
Gavlar: 2 ⋅ 3, 2 ⋅ 0,8 m 2 +
2
Totalarea: (12,16 + 5,12 + 8,64) m2 = 25,92 m2 ≈ 26 m2
Svar: Den minsta mängden tyg är 26 m2.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5115
Se bokens ledning samt lösningen i facit.
5116
Se facit.
5117
Tomtens area: 37 · 26 m2 = 962 m2
Husets area: 15 · 6 m2 + 5,5 · 5 m2 = 117,5 m2
117, 5
Huset upptar
≈ 0,12 = 12% av tomten.
962
Svar: 12% av tomten upptas av huset
5118
Flaggans längd L = (60 + 24 + 108) cm = 192 cm
Flaggans höjd H = (48 + 24 + 48) cm = 120 cm
Flaggans totala area A = 192 · 120 cm2 = 23040 cm2
Korsets area är (24 ⋅120 + 24 ⋅192 − 24 ⋅ 24) cm 2 = 6912 cm 2 (Kan räknas ut på fler sätt)
6912
Korset upptar
= 0,30
23040
Svar: Korset upptar 30% av flaggans area.
5119, 5120 Se bokens ledning samt lösningen i facit.
5121, 5122, Se facit.
5123, 5124
Det är bra att kunna göra enhetsomvandling själv
på det sätt som visas i exemplet på sidan 213.
5125
Omvandla så att det blir samma enhet på de areor som skall jämföras med varandra.
5126
Omvandla så att det blir samma enhet på de areor som skall multipliceras med varandra.
a) 20 m = 2000 cm Æ Arean = 2000 cm · 2 cm = 4000 cm2
b) 2 cm = 0,02 m Æ Arean = 2 m · 0,02 m = 0,04 m2
5127
a) 1 ha = 100 m · 100 m = 10000 m2
b) Skogsområdet är 1500 m · 350 m = 525000 m2 =
525000
ha = 52,5 ha
10000
5128
Exempel som löses i boken
5129
Cirkelns omkrets är π d där d är cirkelns diameter.
OBS! I många formelsamlingar finns formeln 2π r där r är cirkelns radie
Cirkelns area är A = π r 2 där r är cirkelns radie.
a) Omkretsen är 8π cm ≈ 25 cm
Arean är π r 2 = π 42 cm 2 = 16π cm2 ≈ 50 cm2
b) Omkretsen är 10π cm ≈ 31 cm
Arean är π r 2 = π 52 cm 2 = 25π cm2 ≈ 79 cm2
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5130
a) Arean är hälften av cirkelns area
π r 2 π 202
cm 2 = 200π cm 2 ≈ 628 cm 2 ≈ 630 cm 2
→ A=
=
2
2
Omkretsen är halva cirkelns omkrets plus diametern
πd
→
+ d = π r + d = 20π cm + 40 cm ≈ 103 cm
2
Svar: Omkretsen är 103 cm och arean är 630 cm2 .
1
av cirkelns area
4
π r 2 π 252
cm 2 = 156, 25π cm 2 ≈ 491 cm 2 ≈ 490 cm 2
→ A=
=
4
4
Omkretsen är en fjärdedel av cirkelns omkrets plus diametern
πd
πr
25π
cm + 2 ⋅ 25 cm ≈ 89 cm
→
+d =
+ 2r =
4
2
2
Svar: Omkretsen är 89 cm och arean är 490 cm2.
b) Arean är
5131
Se facit. Cirkeln omkrets kan också beräknas med formeln 2π r .
5132
Cirkelns omkrets är π d där d är cirkelns diameter.
OBS! I många formelsamlingar finns formeln 2π r där r är cirkelns radie
Cirkelns area är A = π r 2 där r är cirkelns radie.
a) Omkretsen är 10π cm ≈ 31 cm
Arean är π r 2 = π 52 cm 2 = 25π cm2 ≈ 79 cm2
b) Omkretsen är 2 ⋅1,5π cm ≈ 9,4 cm
Arean är π r 2 = π 1,52 cm 2 = 2, 25π cm2 ≈ 7,1 cm2
5133
Räkna på samma sätt som 5130 a).
5134
Skivan kostar 240 kr/m2.
Skivans area är π r 2 = 0, 622 π m 2 ≈ 1, 2076 m 2 .
Æ Skivan kostar 1,2076 · 240 kr ≈ 289,8 kr ≈ 290 kr
Svar: Skivan kostar 290 kr.
5135
Cykelhjulet är 28 tum i diameter.
1 tum är 2,54 cm
Æ Cykelhjulets diameter är 28 ⋅ 2,54π cm ≈ 223,43 cm
1 km = 1000 m = 100000 cm
100000
varv ≈ 447,57 varv på 1 km.
223, 43
Svar: Cykelhjulet surrar 448 varv på 1 km.
Cykel hjulet snurrar
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5136
Gräsmattans ursprungliga area: A = bh = 18 ⋅12 m 2 = 216 m 2
Area för en rabatt:

A = π r2
2
2
2
 → A = π 3 m = 9π m
r = d / 2 = 6, 0 / 2 m = 3, 0 m 
Rabatternas totala area: 18π m 2
18π
Rabatterna upptar
≈ 0, 26 = 26 % av ytan.
216
Svar: Rabatterna upptar 26% av gräsmattans ursprungliga area
5137
a) Kvadratens omkrets: 4 · 4,2 cm = 16,8 cm
Cirkelns omkrets: 5π cm ≈ 15, 7 cm
Svar: Kvadraten har den största omkretsen
b) Kvadratens area: 4,2 · 4,2 cm2 = 17,64 cm2
Cirkelns area: 2,52 π cm 2 ≈ 19, 6 cm2
Svar: Cirkeln har den största arean.
5138
Området kan delas in i flera delområden.
Den totala arean är summan av de ingående delarnas areor.
Området delas enklast in i en rektangel, 3,6 cm x 2,6 cm,
och två halvcirklar med radien 1,3 cm.
Rektangelns area är 3, 6 ⋅ 2, 6 cm 2 = 9,36 cm 2
Arean för två halvcirklar är 2 ⋅
π r2
= π r 2 = π ⋅1,32 cm 2 ≈ 5,309 cm 2
2
Sammanlagda arean är 9,36 cm2 + 5,309 cm2 ≈14,67 cm2 ≈ 15 cm2
Svar: Områdets area är 15 cm2
5139, 5140, 5141 Se bokens ledning samt lösningen i facit
Kapitel 5.2
5201
Exempel som löses i boken
5202
a) Kubens sidlängd är a.
Kubens volym är a 3 = 6, 03 cm3 = 216 cm3 ≈ 220 cm3
Kuben area är 6a 2 = 6 ⋅ 6, 02 cm 2 = 216 cm 2 ≈ 220 cm 2
b) Rätblockets sidlängder är a, b och c.
Rätblockets volym är abc = 4,5 ⋅ 3, 4 ⋅ 2, 6 cm3 = 39, 78 cm3 ≈ 40 cm3
Rätblockets area är 2(ab + ac + bc) →
2(4,5 ⋅ 3, 4 + 4,5 ⋅ 2, 6 + 3, 4 ⋅ 2, 6) cm 2 = 71, 68 cm 2 ≈ 72 cm 2
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5203
a) V = π r 2 h = π ⋅ 3, 02 ⋅ 7, 0 cm3 ≈ 198 cm3 ≈ 200 cm3
b) A mantel = 2π rh = π dh = π ⋅ 6, 0 ⋅ 7, 0 cm 2 ≈ 131,9 cm 2 ≈ 130 cm 2
c) Totala arean är mantelytans area plus bottenytan plus toppen.
A botten = A topp = π r 2 = π ⋅ 3, 02 cm 2 ≈ 28, 27 cm 2 ≈ 30 cm 2
A total = (42π + 9, 0π + 9, 0π ) cm 2 = 60π cm 2 ≈ 188 cm 2 ≈ 190 cm 2
5204
a) I Kubens bottenarea är 8, 02 cm 2 = 64 cm 2
II Rätblockets bottenarea är 9, 0 ⋅ 6,8 cm 2 = 61, 2 cm 2 ≈ 61 cm 2
b) I Kubens volym är 8, 03 cm3 = 512 cm3 ≈ 510 cm3
II Rätblockets volym är 9, 0 ⋅ 6,8 ⋅ 5, 2 cm3 = 318, 24 cm3 ≈ 320 cm3
5205
I Kuben area är 6 ⋅ 8, 02 cm 2 = 384 cm 2 ≈ 380 cm 2
II Rätblockets area är 2(9, 0 ⋅ 6,8 + 9, 0 ⋅ 5, 2 + 6,8 ⋅ 5, 2) cm 2 = 286, 72 cm 2 ≈ 290 cm 2
5206
a) Basytans area är π r 2 = π ⋅ 202 cm 2 ≈ 1256 cm 2 ≈ 1300 cm 2
b)
5207
V = π r 2 h = π ⋅ 202 ⋅ 70 cm3 ≈ 87964 cm3 ≈ 88000 cm3
a) A mantel = 2π rh = π dh = π ⋅ 40 ⋅ 70 cm 2 ≈ 8796 cm 2 ≈ 8800 cm 2
b) Totala arean är mantelytans area plus bottenytan plus toppen.
A botten = A topp = π r 2 = π ⋅ 202 cm 2 ≈ 28, 27 cm 2 ≈ 30 cm 2
A total = (2800π + 400π + 400π ) cm 2 = 3600π cm 2 ≈ 11309, 7 cm 2 ≈ 11000 cm 2
5208
V = π r 2 h = π ⋅ 0,152 ⋅180 m3 ≈ 12, 72 m3 ≈ 13 m3
Svar: Röret tar upp 13 m3.
5209
V = π r 2 h = π ⋅ 6, 42 ⋅ 3, 6 m3 ≈ 463, 2 m3 ≈ 460 m3
Svar: Brunnen innehåller 460 m3 gödsel.
5210
Mjölkförpackningen har samma form som ett rätblock.
Arean är 2(9,5 ⋅ 6, 4 + 9,5 ⋅16, 4 + 6, 4 ⋅16, 4) cm 2 = 643,12 cm 2 ≈ 640 cm 2
5211
Rummets mått: 19 m × 31 m × 5,0 m
Luftens densitet är 1,3 kg/m3.
Rummets volym (tomt) är 19 ⋅ 31⋅ 5, 0 m3 = 2945 m3
Luften väger 2945 m3 ⋅1,3 kg/m3 = 3828,5 kg ≈ 3800 kg
Svar: Luften i lagerlokalen väger 3800 kg.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5212
Låt till exempel den lilla lådan ha måtten
a = 1 cm, b = 2 cm och c = 3 cm.
Eftersom alla motsvarande sidor på den stora
lådan är dubbelt så långa har du
A = 2 cm, B = 4 cm, C = 6 cm.
a)
b
a
c
Lilla lådans area är
2(ab + ac + bc) = 2(1 ⋅ 2 + 1⋅ 3 + 2 ⋅ 3) cm 2
B
= 2(2 + 3 + 6) cm 2 = 22 cm 2
Stora lådans area är
2( AB + AC + BC ) = 2(2 ⋅ 4 + 2 ⋅ 6 + 4 ⋅ 6) cm 2
A
C
= 2(8 + 12 + 24) cm = 88 cm
Svar: Den stora lådans area är fyra gånger
så stor som den lilla lådans area.
2
b)
2
Lilla lådans volym är
abc = 1⋅ 2 ⋅ 3 cm3 = 6 cm3
Stora lådans volym är
ABC = 2 ⋅ 4 ⋅ 6 cm3 = 48 cm3
Svar: Den stora lådans volym är åtta gånger
så stor som den lilla lådans volym.
Vill man visa detta på ett mer generellt sätt gör man så här:
Låt den lilla lådans sidlängder vara a, b, och c → VL = abc, A L = 2(ab + ac + bc)
Stora lådans sidlängder är då 2a, 2b och 2c
 A S = 2(2a ⋅ 2b + 2a ⋅ 2c + 2b ⋅ 2c) = 4 ⋅ 2(ab + ac + bc) = 4 A L
→ 
VS = 2a ⋅ 2b ⋅ 2c = 8abc = 8VL
a) Den stora lådans area är fyra gånger så stor som den lilla lådans area.
b) Den stora lådans volym är åtta gånger så stor som den lilla lådans volym.
5213
Låt cylinder A t ex ha följande mått:
r = 4 cm
h = 5 cm
Då får cylinder B ha följande mått:
r = 2 cm
h = 10 cm
Volymen blir då
V = π r 2 h = π ⋅ 42 ⋅ 5 cm3 = 80π cm3
Volymen blir då
V = π r 2 h = π ⋅ 22 ⋅10 cm3 = 40π cm3
Svar: Cylinder B har mindre volym än cylinder B.
Vill du visa det generellt gör du så här:
Cylinder A har radien r och höjden h. Cylinder B har då radien r/2 och höjden 2h.
Volymen för cylinder A är VA = π r 2 h .
2
2π r 2 h π r 2 h VA
r
=
=
Volymen för cylinder B är VB = π   ⋅ 2h =
.
4
2
2
 2
Æ Cylinder B har hälften så stor volym som cylinder A.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5214
Den yta som skall målas är mantelarean (”väggen”) och toppen (taket).
Cisternen är 25 m hög och har en radie på 25 m.
1 liter färg täcker 10 m2, man skall måla två lager.
Den yta som skall målas är
A vägg + A tak = 2π rh + π r 2 = (2π ⋅ 25 ⋅ 25 + π ⋅ 252 ) m 2 ≈ 5890,5 m 2
Eftersom ytan skall målas två gånger måste detta svar fördubblas → 11781 m 2
11781
Färgen skall alltså räcka till 11781 m2 →
liter = 1187,1 liter ≈ 1200 liter .
10
Svar: Man behöver 1200 liter färg.
5215
a
b
h=?
c
a = 6,5 cm
b = 33, 0 cm
c = 15, 4 cm
r = 9, 0 cm
VLÅDA = abc = 6,5 ⋅ 33, 0 ⋅15, 4 cm3 = 3303,3 cm3
VCYL = π r 2 h = π ⋅ 9, 02 h = 81π h
r
För att vattnet skall rymmas i cylindern måste VLÅDA = VCYL, det vill säga
81π h = 3303,3 cm3 →
3303,3
h=
cm ≈ 12,98 cm ≈ 13 cm
81π
Svar: Cylinderns höjd måste vara minst 13 cm hög.
5216
Se bokens ledning samt lösningen i facit.
5217
Stapelns längd är 18 m och dess bredd är 3,0 m.
Stapelns medelhöjd är
1,51 + 1, 70 + 1, 49 + 1, 62 + 1, 73 + 1, 68 + 1,56 + 1,57 + 1, 43 + 1,59
m ≈ 1,588 m
10
Stapelns volym är 18 ⋅ 3, 0 ⋅1,588 m3 ≈ 85, 752 m3 ≈ 86 m3
Svar: Vedstapelns volym är ca 86 m3.
5218, 5219 Se bokens ledning samt lösningen i facit
5220, 5221 Se facit.
5222, 5223
5224
Det är bra att kunna göra enhetsomvandling
själv på det sätt som visas i exemplet på sidan 213.
Omvandla så att alla volymerna har samma enhet, t ex dm3
600 liter = 600 dm3,
0,45 m3 = 450 dm3,
500 000 ml = 500 liter = 500 dm3
Svar: 0,45 m3, 500 000ml, 560 dm3, 600 liter
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5225
Tankens mått är 16 ⋅ 20 ⋅ 50 cm3 = 1, 6 ⋅ 2, 0 ⋅ 5,0 dm3 = 16 dm3 = 16 liter
Svar: Tanken rymmer 16 liter
5226
Tanken rymmer 3,2 m3 = 3200 liter.
Förbrukningen är 20 liter per dygn.
Innehållet räcker
3200 l
= 160 dygn
20 l/dygn
Svar: Tankens innehåll räcker 160 dygn.
5227
Se bokens ledning samt lösningen i facit.
5228, 5229 Exempel som löses i boken.
5230
a) Konens basarea är π r 2
I r = 3, 0 cm → π r 2 = π ⋅ 3, 02 cm 2 ≈ 28 cm 2
II r = 48 cm → π r 2 = π ⋅ 482 cm 2 ≈ 7238 cm 2 ≈ 7200 cm 2
b) Konens volym är
π r 2h
3
I r = 3, 0 cm, h = 6, 0 cm → π r 2 h / 3 = π ⋅ 3, 02 ⋅ 6,0/3 cm3 ≈ 57 cm3
II r = 48 cm, h = 90 cm → π r 2 h / 3 = π ⋅ 482 ⋅ 90/3 cm3 ≈ 217147 cm3 ≈ 210000 cm3
5231
r = 13 cm
4π r 3
3
2
Klotets area beräknas med formeln A = 4π r
Klotets volym beräknas med formeln V =
4π ⋅133
V=
cm3 ≈ 9202,8 cm3 ≈ 9200 cm3 = 9, 2 dm3
3
A = 4π ⋅132 cm 2 ≈ 2123, 7 cm 2 ≈ 2100 cm 2 = 21 cm 2
Svar: Klotets volym är 9200 cm3 och klotets area är 2100 cm2.
5232
r = 16 cm
Halvklotets area är ”hälften av klotets area” + ”basytan” (den plana ytan).
A klot
4π r 2
+ A cirkel =
+ π r 2 = 3π r 2 = 3π ⋅162 cm 2 ≈ 2413 cm 2 ≈ 24 dm 2
A=
2
2
Svar: Halvklotets area är ca 24 dm2.
5233
Se facit.
5234
a) Konens basarea är π r 2
I r = 8, 0 cm → π r 2 = π ⋅ 8, 02 cm 2 ≈ 201 cm 2 ≈ 200 cm 2
II r = 30 mm → π r 2 = π ⋅ 302 mm 2 ≈ 2827 mm 2 ≈ 28 cm 2
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
b) Konens volym är
π r 2h
3
I r = 8, 0 cm, h = 8, 0 cm → π r 2 h / 3 = π ⋅ 8, 03 /3 cm3 ≈ 536 cm3 ≈ 540 cm3
II r = 30 mm, h = 60 mm → π r 2 h / 3 = π ⋅ 302 ⋅ 60/3 mm3 ≈ 56549 mm3 ≈ 57 cm3
5235
r = 8,0 cm
4π r 3 3 2π r 3 2π ⋅ 8, 03
=
=
cm3 ≈ 1072 cm3
2
3
3
b) Arean för en cirkel → A = π r 2 = π ⋅ 8, 02 cm 2 ≈ 201 cm 2 ≈ 200 cm 2
a) Hälften av klotets volym → V =
4π r 2
= 2π r 2 = 2π ⋅ 8, 02 cm 2 ≈ 402 cm 2 ≈ 400 cm 2
2
d) Summan av areorna i b) och c) A = π r 2 + 2π r 2 = 3π r 2 = 3π ⋅ 8, 02 cm 2 ≈ 600 cm 2
c) Hälften av klotets area → A =
5236
r = 673 mil
Jordklotets area beräknas med formeln A = 4π r 2
A = 4π ⋅ 637 2 mil2 ≈ 5099044 mil2 ≈ 5100000 mil2 = 5,10 ⋅106 mil2
Svar: Jordens area är ca 5,10 miljoner mil2. (OBS! Fel enhet i bokens facit)
5237
Diametern ä 8,4 cm Æ r = 4,2 cm
Apelsinens volym beräknas med formeln V =
4π r 3
3
4π ⋅ 4, 23
cm3 ≈ 310 cm3
3
Svar: Klotets volym är 9200 cm3 och klotets area är 2100 cm2.
V=
5238
r = 5,2 cm
Stålets densitet är
7,8 ton 7,8 ⋅1000 kg 7,8 ⋅1000000 g
=
=
= 7,8 g/cm3
m3
1000000 cm3 1000000 cm3
Kulans volym beräknas med formeln V =
4π r 3
3
4π ⋅ 5, 23
cm3 ≈ 588,997 cm3
3
Multiplicera volymen med densiteten för att beräkna hur mycket kulan väger.
7,8 ⋅ 4π r 3
→
≈ 7,8 ⋅ 588,997 g ≈ 4594 g ≈ 4, 6 kg
3
Svar: Kulan väger 4,6 kg
V=
5239
Konens volym är
π r 2h
3
r = 4, 0 cm, h = 6, 0 cm →
π r 2h
3
=
π ⋅ 4, 02 ⋅ 6,0
Svar: Glaset rymmer 10 cl.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
3
cm3 ≈ 101 cm3 = 101 ml ≈ 10 cl
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5240
r = 3, 0 cm, h = 10 cm
Glassen är sammansatt av en kon och ett halvt klot
Konens volym är
π r 2h
3
=
π ⋅ 3, 02 ⋅10
3
cm3 ≈ 94, 25 cm3
4π r 3 3 2π r 3 2π ⋅ 3, 03
=
=
cm3 ≈ 56,55 cm3
2
3
3
Totala volymen blir (94,25 + 56,55) cm3 ≈ 150,80 cm3 ≈ 150 cm3.
Hälften av klotets volym → V =
Svar: Glassens volym är 150 cm3 .
5241
Se bokens ledning samt lösningen i facit.
5242
Exempel som löses i boken.
5243
Tips: Det är oftast enklast att göra enhetsomvandlingarna före man beräkningarna.
Cylinderns mått omvandlas till mm för att få samma volymsenhet som droppen.
1. Cylinderns volym
2.
r = 24 mm
r = 1,5 mm
h = 36 mm
Droppens volym
4π ⋅1,53
V=
mm3 = 4,5π mm3
3
VCYL = π r h
2
h
Droppens volym
= π ⋅ 242 ⋅ 36
= 20736π mm3
r
20736π
20736
droppar =
droppar = 4608 droppar ≈ 4600 droppar
4,5π
4,5
Svar: Cylindern rymmer 4600 droppar.
Cylindern rymmer
5244
Se bokens ledning samt lösningen i facit.
5245
Rymdkapseln är sammansatt av en kon och ett halvt klot
Halvklotets diameter är 4,0 m Æ radien är 2,0 m
Æ den koniska delen är (5,0 − 3,0) m = 3,0 m lång.
r = 2, 0 m, h = 3, 0 m
12π 3
m = 4π m3 ≈ 12,566 m3
3
3
3
3
4π r 3 2π r 3 2π ⋅ 2, 03 3 16π 3
Hälften av klotets volym → V =
=
=
m =
m ≈ 16, 755 m3
2
3
3
3
12π 16π
28π 3
+
) m3 =
m ≈ 29,32 m3 ≈ 30 m3
Totala volymen blir ( (
3
3
3
Svar: Rymdkapselns volym är 30 m3 .
Konens volym är
π r 2h
=
π ⋅ 2, 02 ⋅ 3,0
m3 =
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5246
Konens radie är 60 mm och höjden 90 mm.
π r 2 h π ⋅ 602 ⋅ 90
Konens volym är
=
mm3 = 108000π mm3 .
3
3
Droppens radie är 1,5 mm
4π ⋅1,53
mm3 = 4,5π mm3
3
108000π
108000
droppar =
droppar = 24000 droppar
Konen rymmer
4,5π
4,5
Svar: Konen rymmer 24000 droppar.
Volymen för en droppe är
5247, 5248, 5249 Se bokens ledning samt lösningen i facit.
5250
Exempel som löses i boken.
5251
a) Prismats basyta är 5, 6 ⋅ 4, 0/2 cm 2 = 11, 2 cm 2
Prismats höjd är 4,8 cm Æ Prismats volym är 11, 2 ⋅ 4,8 cm3 = 53, 76 cm3 ≈ 54 cm3
Svar: Prismats volym är 54 cm3.
b) Pyramidens basyta är 15 ⋅16/2 cm 2 = 120 cm 2
Pyramidens höjd är 18 cm Æ Pyramidens volym är 120 ⋅18/3 cm 3 = 720 cm3
Svar: Pyramidenss volym är 54 cm3.
5252
a) Prismats basyta är en triangel med längden 3,6 cm och höjden 2,0 cm.
Æ Prismats basyta är 3, 6 ⋅ 2, 0/2 cm 2 = 3, 6 cm 2
Svar: Prismats basyta är 3,6 cm2.
b) Prismats höjd är 4,0 cm Æ Prismats volym är 3, 6 ⋅ 4, 0 cm3 = 14, 4 cm3 ≈ 14 cm3
Svar: Prismats volym är 14 cm3.
5253
a) Pyramidens basyta är en rektangel med längden 16 cm och höjden 8 cm.
Æ Pyramidens basyta är 16 ⋅ 8 cm 2 = 128 cm 2 ≈ 130 cm 2
Svar: Pyramidens basyta är 130 cm2.
b) Höjden är 9 cm Æ Pyramidens volym är 128 ⋅ 9/3 cm3 = 384 cm3 ≈ 380 cm3
Svar: Pyramidens volym är 190 cm3.
5254
Se figuren i facit.
Bh
, där B är basarean och h är höjden.
3
B = 2,80 ⋅ 2,80 m 2 
2,802 ⋅1,80 3
m ≈ 4, 7 m3
→
V
=

3
h = 1,80 m

Tältets volym är V =
Svar: Tältets volym är 4,7 m3.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5255
Toppens volym är VTOPP =
B = 1, 4 ⋅1, 4 dm 2 
 → VTOPP
h = 1,15 dm

Bh
, där B är basarean och h är höjden.
3
1, 42 ⋅1,15
dm3
=
3
Lådans volym är VLÅDA = 1, 4 ⋅1, 4 ⋅1, 6 m3
Holkens totala volym är 1, 4 ⋅1, 4 ⋅1, 6 dm3 + 1, 42 ⋅1,15/3 dm3 ≈ 3,9 dm3 = 3,9 liter
Svar: Holken rymmer (tom) 3,9 liter luft (om givna mått är innermått).
5256, 5257 Se bokens ledning samt lösningen i facit.
Kapitel 5.3
5301
Exempel som löses i boken
5302
Vinkelsumman i en triangel är 180D .
a) Vinkel C = 180D − 80D − 40D = 60D
b) Vinkel E = 180D − 120D − 25D = 35D
5303
Vinkelsumman i en rektangel är 360D
a) Vinkel A = 360D − 106D − 2 ⋅ 62D = 130D
b) Vinkel M = 360D − 100D − 70D − 110D = 80D
5304
a) 108D + 30D = 138D
b) Vinkel B = 180D − 138D = 42D eller
vinkel B = 180D − 108D − 30D = 42D
a) 2 ⋅114D + 44D = 272D
b) Vinkel D = 360D − 272D = 88D eller
vinkel D = 360D − 2 ⋅114D − 44D = 88D
5305
5306
x = 180 − 55 − 27 = 98
Svar: Man ser sträckan AB under synvinkeln 98D .
5307
Vinkelsumman i en rektangel är 360D
Vinkel A = 360D − 84D − 2 ⋅118D = 40D
Svar: Vinkeln vid drakens svans är 40D .
5308
Ta kontakt med din lärare om du vill diskutera din lösning.
5309
En trubbig vinkel är större än 90D . Det betyder att summan av två trubbiga vinklar blir
större än 180D . Eftersom en triangel har vinkelsumman 180D kan det bara finnas en
trubbig vinkel i en triangel.
En rektangel kan ha två trubbiga vinklar, se t ex figurerna i uppgift 5303.
5310
Se bokens ledning samt lösningen i facit
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5311
Exempel som löses i boken.
Vinkeln u ligger utanför triangeln. En vinkel som ligger på detta sätt
har en speciell benämning: yttervinkel.
Yttervinkeln u är alltid lika stor som summan av vinklarna z och w.
w
u=z+w
z
5312
5313
5314
a)
b)
a)
b)
u
v = 28D + 22D = 50D
v = 105D − 60D = 45D
v = 33D + 49D = 82D
v = 137D − 25D = 112D
x = 47 − 18 = 29
Svar: Båten syns från fönstret under höjdvinkeln 29D
OBS! I bilden står det x D , därför tas inte gradtecknet med i uträkningen
5315, 5316 Se bokens ledning samt lösningen i facit.
5317
Exempel som löses i boken.
5318
Vinkelsumman i en triangel är 180D .
a) Vinkel A = 180D − 2 ⋅ 70D = 40D
180D − 38D
b) Vinkel E = Vinkel F =
= 71D
2
5319
Vinkelsumman i en triangel är 180D .
Vinkel M = Vinkel L = 38D → Vinkel K = 180D − 2 ⋅ 38D = 104D
5320
Vinkelsumman i en triangel är 180D .
a) Vinkel C = 180D − 90D − 23D = 67D
5321
5322
b) Vinkel K = 180D − 90D − 59,3D = 30, 7D
En rätvinklig triangel är likbent om de två andra vinklarna är
180D − 90D
= 45D
2
Om vinkeln A är rät i en triangel ABC är vinkelsumman för vinklarna B och C 90D
a) 34D + 66D = 100D ≠ 90D
c) 42,5D + 48,5D = 91D ≠ 90D
Svar: Triangeln är inte rätvinklig
Svar: Triangeln är inte rätvinklig
b) 17D + 73D = 90D
Svar: Triangeln är rätvinklig
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
d) 9,1D + 80,9D = 90D
Svar: Triangeln är rätvinklig
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5323
Vinkelsumman i en triangel är 180D → högst en trubbig vinkel i triangeln.
a) 2 ⋅ 25D + 130D = 180D
c) 2 ⋅ 35D + 115D = 185D ≠ 180D
Svar: Triangeln är likbent
Svar: Triangeln är inte likbent
b) 2 ⋅ 45D + 80D = 170D ≠ 180D
2 ⋅ 80D + 45D = 205D ≠ 180D
Svar: Triangeln kan inte vara likbent.
5324
d) 2 ⋅ 38D + 104D = 180D
Svar: Triangeln är likbent
180D − 24D
a) Basvinklarna är
= 78D
2
b) Basvinklarna minskar med totalt 6D . För att triangeln skall fortsätta vara likbent
måste ändringen vara lika stor för båda vinklarna, dvs 6D / 2 = 3D
c) Om de två basvinklarna ökar 6D vardera blir den totala ökningen 12D . Därför måste
toppvinkeln minska 12D eftersom triangelns vinkelsumma är konstant.
5325
Se facit.
5326
Vinkelsumman i en triangel är 180D .
Låt vinkeln vid triangelns spetsvara u D . En basvinkel är då u D + 9D
Vi har alltså
u + 2(u + 9) = 180
3u + 18 = 180
u = 54 → u + 9 = 63
Svar: Triangelns vinklar är 54D , 63D och 63D
5327
Vinkelsumman i en triangel är 180D .
a) Basvinkeln är 180D − 115D = 65D
x = 180D − 2 ⋅ 65D = 50D
Svar: Vinkeln är 50D
b) Med hjälp vad vi vet om yttervinkeln från detta facit till uppgift 5311 ser vi att
2 x = 110D → x = 55D
Svar: Vinkeln är 55D
5328, 5329 Se bokens ledning samt lösningen i facit.
5330
Exempel som löses i boken.
5331
Ett halvt varv är 180D .
a) x + 2 x = 180D
b)
x + x + 42D = 180D
3x = 180D
2 x = 138D
x = 60D → 2 x = 120D
Svar: Vinklarna är 60D och 120D
x = 69D → x + 42D = 111D
Svar: Vinklarna är 69D och 111D
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5332
Vinkelsumman i en triangel är 180D .
a)
x + x + 16D + 58D = 180D
b)
2 x = 180D − 58D − 16D
5 x = 180D
x = 53D
x = 36D
→ x + 16D = 69D
Svar: Vinklarna är 53D , 58D och 69D
5333
Svar: Vinklarna är 36D , 72D och 72D
100D + 108D + 2 x = 360D
b)
2 x = 300D
x = 76D
→ x − 80D = 70D och x − 20D = 130D
b)
x + 4 x = 180D
x = 36D
x + x + 26D = 180D
2 x + 26D = 180D
→
4 x = 144D
x = 77D
Svar: Vinklarna är 36D och 144D
→ x + 26D = 103D
Svar: Vinklarna är 77D och 103D
Vinkelsumman i en triangel är 180D .
a)
x + 80D + 45D = 180D
b)
x + 90D + 35D = 180D
x = 180D − 125D
x = 180D − 125D
x = 55D
x = 55D
Svar: Vinkeln x är 55D
Svar: Vinkeln x är 55D
Vinkelsumman i en triangel är 180D .
a)
5337
→ x = 150D
Svar: 70D , 70D , 90D och 130D
5 x = 180D
5336
x − 80D + 70D + x − 20D + 90D = 360D
2 x = 152D
Svar: 76D , 76D , 100D och 108D
Ett halvt varv är 180D .
a)
5335
→ x = 72D
Vinkelsumman i en rektangel är 360D
a)
5334
x + 2 x + 2 x = 180D
x + x + 20D + 50D = 180D
b)
x + 2 x + 93D = 180D
2 x = 180D − 50D − 20D
3x = 180D − 93D = 87D
x = 55D → x + 20D = 75D
x = 29D → 2 x = 58D
Svar: Vinklarna är 50D , 55D och 75D
Svar: Vinklarna är 29D , 58D och 93D
Vinkelsumman i en rektangel är 360D
a)
x + 105D + 115D + x + 10D = 360D
b)
x + 82D + x + 58D = 360D
2 x = 360D − 230D = 130D
2 x = 360D − 82D − 58D = 220D
x = 65D
x = 110D
Svar: 65D , 75D , 105D och 115D
Svar: 58D , 82D , 110D och 110D
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5338
Vinkelsumman i en triangel är 180D .
a)
5339
5340
b)
x + 3 x + x + 15D = 180D
x + x = 124D
5 x = 180D − 15D = 165D
2 x = 124D
x = 33D
x = 62D
Svar: Vinkeln x är 33D
Svar: Vinkeln x är 62D
Vinkelsumman i en triangel är 180D .
a)
Se även uppgift 5311
Se även uppgift 5311
Vinkel B är 2x.
x + 2 x = 75D
b) Vinkel B är x.
94D + x = 3 x
3x = 75D
2 x = 94D
x = 25D → 2 x = 50D
x = 47D
Svar: Vinkeln B är 50D
Svar: Vinkeln B är 47D
Låt den vinkeln vid triangelns topp vara x. Basvinkeln är då 2x.
x + 2 x + 2 x = 180D
5 x = 180D
x = 36D → 2x = 72D
Svar: Triangeln vinklar är 36D , 72D och 72D . Se figuren i facit.
5341
4 x + 5 x + 6 x = 180D
15 x = 180D
→ 4x = 48D
x = 12D
Svar: Triangelns minsta vinkel är 48D . Se figuren i facit.
5342, 5343 Se bokens ledning samt lösningen i facit.
5344
a) x + 40D = 110D → x = 50D
b) x + 30D = 3 x → 2x = 30D → x = 15D
5345
Se bokens ledning samt lösningen i facit.
5346
Exempel som löses i boken.
5347
Bågen är
50
5
=
av omkretsen., omkretsen är 2π r , r = 2,5 cm
360 36
5
10π r 25π
⋅ 2π r =
=
Bågens längd är
cm ≈ 2,18 cm.
36
36
36
Svar: Bågens längd är 2,2 cm
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
50
5
=
av arean., arean är A = π r 2 , r = 2,5 cm
360 36
5
5π ⋅ 2,52
Sektorns area är
⋅π r 2 =
cm 2 ≈ 2,73 cm 2 .
36
36
Svar: Sektorns area är 2,8 cm2.
b) Sektorn är
5348
72 1
= av hela cirkeln.,
360 5
Omkretsen för en cirkel är 2π r ,
Arean för en cirkel är A = π r 2 ,
r = 12 cm
1
2π r 24π
=
cm = 4,8π cm ≈ 15,08 cm.
Bågens längd är ⋅ 2π r =
5
5
5
Sektorns omkrets är (12 + 12 + 4,8π ) cm ≈ 39, 08 cm ≈ 39 cm
Sektorn är
1
π ⋅122
⋅π r 2 =
cm 2 ≈ 90,48 cm 2 .
5
5
Svar: Sektorns omkrets är 39 cm och sektorns area är 90 cm2.
Sektorns area är
5349
38
av omkretsen., omkretsen är 2π r , r = 6,2 cm
360
38
76π r 76π ⋅ 6, 2
⋅ 2π r =
=
Bågens längd är
cm ≈ 4,11 cm.
360
360
360
Svar: Bågens längd är 4,1 cm
a) Bågen är
38
av arean., arean är A = π r 2 , r = 6,2 cm
360
38
38π ⋅ 6, 22
Sektorns area är
⋅π r 2 =
cm 2 ≈ 12,75 cm 2 .
360
360
Svar: Sektorns area är 13 cm2.
b) Sektorn är
5350
a)
v

⋅ 2π r = 4,5
4,5 ⋅ 360D
D
→
=
≈ 52D
v
360

π
⋅
2
5,
0

r = 5, 0
Svar: Medelpunktsvinkeln är 52D
b)

1620D

4,5r
10π
≈ 11 cm 2
→ A=
2
v
A=
⋅π r 2 
D

360
v=
Svar: Cirkelsektorns area är 11 cm2.
5351, 5352, 5353 Se bokens ledning samt lösningen i facit.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
Kapitel 5.4
5401, 5402, 5403 Exempel som löses i boken
5404
Skalan uttrycks som
Se facit.
a) Exempel:
bild : verklighet
1
⋅1 cm = 0, 02 cm = 0, 2 mm på bilden.
50
1
Ett föremål som är 20 m i verkligheten är
⋅ 20 m = 0, 4 m på bilden.
50
Ett föremål som är 1 cm i verkligheten är
b) Exempel:
Ett föremål som är 1 cm i verkligheten är 8 ⋅1 cm på bilden.
Ett föremål som är 52 mm i verkligheten är 8 ⋅ 52 mm = 416 mm ≈ 42 cm på bilden.
om x > y → förstoring
x
Æ
om x < y → förminskning
y
5405
Se facit.
5406
a) Eiffeltornsmodellen blir
1
⋅ 300 m = 3 m hög.
100
b) Eiffeltornsmodellen blir
1
⋅ 300 m = 0, 6 m hög.
500
5407
x : y kan tolkas
1
av verklighetens skottkärra,
40
dvs den riktiga skottkärran är 40 gånger större än modellen.
Skottkärremodellen är
40 ⋅ 4,5 cm = 180 cm = 1,8 m
Svar: Skottkärran är 1,8 m i verkligheten
5408
Se facit och uppgift 5405.
5409
Racketen är 17 gånger större i verkligheten än på bilden
a) 17 ⋅ 4 cm
b) 17 ⋅ 4 cm = 68 cm
Svar: Racketen är 68 cm i verkligheten.
5410
Se facit.
5411
Skala 2:1 betyder att bilden är 2 gånger större än verkligheten.
Verklighetens tärning är hälften så stor som bildens, dvs 1,5 cm/2 = 0,75 cm.
Svar: Tärningssidan är i verkligheten 0,75 cm.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5412
1
av verklighetens längd.
5
Verklighetens boll är fem gånger så stor som bildens, dvs 5 ⋅ 4,9 cm = 24,5 cm .
Skala 1:5 betyder att bildens längd är
Svar: Bollens diameter är i verkligheten 24,5 cm.
5413
Se facit.
5414, 5415 Exempel som löses i boken.
5416
Till skalor används endast heltal
Längd i verkligheten: 24 mm
Skala är bild : verklighet
a) Längd i bild: 12 mm
12 1
12 : 24 =
= = 1: 2
24 2
Svar: Skalan är 1:2
5417
Längd i verkligheten: 8,5 mm
Skala är bild : verklighet
a) Längd i bild: 34 mm
34 4
34 : 8,5 =
= = 4 :1
8,5 1
Svar: Skalan är 4:1
5418
Skala är bild : verklighet
Längd i bild: 5 cm
Längd i verkligheten: 175 cm
5
1
5 :175 =
=
= 1: 35
175 35
Svar: Skalan är 1:35.
5419
b) Längd i bild: 48 mm
48 2
48 : 24 =
= = 2 :1
24 1
Svar: Skalan är 2:1
b) Längd i bild: 1,7 mm
1, 7 1
1, 7 : 8,5 =
= = 1: 5
8,5 5
Svar: Skalan är 1:5
Det måste vara samma längdenhet
för bilden och verkligheten för att
man skall få rätt skala.
Skala är bild : verklighet
Längd i bild: 76 mm
Längd i verkligheten: 19 mil = 190 km = 190 000 m = 190 000 000 mm
76
1
76 :190 000 000 =
=
= 1: 2 500 000
190 000 000 2 500 000
Svar: Skalan är 1:2 500 000
5420, 5421 Exempel som löses i boken.
5422
50000 ⋅ 35 mm = 1750000 mm = 1750 m = 1, 75 km ≈ 1,8 km
Svar: Det är 1,8 km mellan Björkudden och Granbo.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5423
1
⋅ 2400 m = 0, 048 m = 4,8 cm
50000
Svar: På kartan är det 4,8 cm mellan Enbacken och Granbo.
5424
200000 ⋅ 6,5 cm = 1300000 cm = 13000 m = 13 km
Svar: Dagsetappen var 13 km.
5425
I verkligheten är detaljen 3 ⋅ 72 mm = 216 mm .
1
På den andra ritningen är detaljen ⋅ 216 mm = 54 mm
4
Svar: Detaljen är 54 mm på en ritning i skala 1:4.
5426
Höjden mäts på bilden till 25 mm.
Skalan är 1:30.
Räcket skall vara minst 1000 mm högt i verkligheten.
I verkligheten är räcket 30 ⋅ 25 mm = 750 mm
750 mm < 1000 mm
5427
Svar: Räcket är inte tillräckligt högt eftersom det är lägre än 1000 mm.
Se bokens ledning samt lösningen i facit.
5428
Exempel som löses i boken.
5429
a) Sidan DE
b)
c) Sidan EF
8
= 2 Svar: 2 gångers förstoring.
4
d) x = 2 ⋅ 2 = 4
5430
a)
x 6 2
= =
15 9 3
2 ⋅15
x=
= 10
3
Svar: x = 10
b)
x 30 5
=
=
12 18 3
5 ⋅12
= 20
x=
3
Svar: x = 20
5431
a)
x 10 5
=
=
12 8 4
5 ⋅12
x=
= 15
4
Svar: Sidan är 15 cm.
b)
x 30 5
=
=
18 24 4
5 ⋅18
x=
= 22,5
4
Svar: Sidan är 22,5 cm.
5432
x 20 2
y 30 3
=
=
=
=
15 30 3
17 20 2
2 ⋅15
3 ⋅17
x=
= 10
y=
= 25,5 ≈ 26
3
2
Svar: Sidan x = 10 cm och sidan y ≈ 26 cm.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
c)
x 5
=
8 4
5⋅8
= 10
x=
4
Svar: x = 10
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5433
x
21,1
=
0, 7 0,82
21,1 ⋅ 0, 7
x=
≈ 18
0,82
Svar: Flaggstången är 18 m hög.
5434, 5435 Se bokens ledning samt lösningen i facit.
Till skalor används heltal
5436, 5437 Exempel som löses i boken.
5438
a) längdskalan är 2:3 (bild : verklighet)
2
22 4
 2
b) areaskalan = längdskalan Æ   = 2 = = 4 : 9 Æ Areaskalan är 4:9
3
9
 3
2
3
3
8
 2 2
c) volymskalan = längdskalan Æ   = 3 =
= 8 : 27 Æ Volymskalan är 8:27
27
 3 3
3
5439
12, 0
= 3 gånger större än den lilla triangelns bas,
4, 0
det vill säga längdskalan är 3:1
a) Den stora triangelns bas är
2
 3 9
Æ areaskalan = längdskalan2 =   = = 9 :1
1 1
Arean i den stora triangeln är 9 ⋅ 5, 0 cm 2 = 45 cm 2
Svar: Den stora triangelns area är 45 cm2.
2, 0
= 0, 4 av den lilla triangelns bas,
5, 0
det vill säga längdskalan är 2:5
b) Den lilla rektangelns bas är
2
4
 2
Æ areaskalan = längdskalan =   =
= 0,16
25
5
Arean i den lilla rektangeln är 0,16 ⋅10, 0 cm 2 = 1, 6 cm 2
Svar: Den lilla rektangelns area är 1,6 cm2.
2
5440
Samma typ av uppgift 5439a).
T2 är avbildningen.
Den längsta sidan i T2 är 15/45 = 1/3 av motsvarande sida i T1.
Längdskalan är 1:3 Æ areaskalan är 1:9
Arean för T2 är 756 cm2/9 = 84 cm2.
Svar: Arean av T2 är 84 cm2.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5441
8, 0
= 2 gånger större än det lilla rätblockets
4, 0
motsvarande kant, det vill säga längdskalan är 2:1
a) Det stora rätblockets kant är
3
 2  2⋅2⋅2
Æ volymskalan = längdskalan =   =
= 8 :1
1 ⋅1 ⋅1
1
Volymen för det stora rätblocket är 8 ⋅ 20, 0 cm3 = 160 cm3
3
Svar: Det stora rätblockets volym är 160 cm3.
3, 0 1, 0
=
= 0, 25 av det stora prismats
12, 0 4, 0
motsvarande kant, det vill säga längdskalan är 1:4
b) Det lilla prismats kant är
3
1 ⋅1 ⋅1
1
Æ volymskalan = längdskalan3 =   =
= 1: 64
 4  4⋅4⋅4
1
Volymen för det stora prismat är
⋅ 320, 0 cm3 = 5, 0 cm3
64
Svar: Det stora prismats volym är 5,0 cm3.
5442
Se bokens ledning samt lösningen i facit.
5443
Det stora prismats kant är
12 4
=
gånger så stort det lilla prismats
9 3
motsvarande kant, det vill säga längdskalan är 4:3
3
 4  4⋅4⋅4
Æ volymskalan = längdskalan =   =
= 64 : 27
3⋅3⋅3
 3
64
Volymen för det stora kärlet är
⋅1, 08 liter = 2,56 liter ≈ 2,6 liter
27
3
Svar: Det stora kärlets volym är 2,6 liter.
5444
Se bokens ledning samt lösningen i facit.
Kapitel 5.5
Om du har en miniräknare med x2-knapp
trycker du
5501, 5502 Exempel som löses i boken.
5,7 x2
5503
för att beräkna 5,72
a) kvadraten på 5,7 skrivs 5, 7 2 . Beräkningen är 5, 7 ⋅ 5, 7 .
5, 7 2 = 32, 49
b) kvadraten på 0,41 skrivs 0, 412 . Beräkningen som skall göras är 0, 41 ⋅ 0, 41 .
0, 412 = 0,1681
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5504
5505
a) 352 + 462 = (1225 + 2116) = 3341
När du räknar med miniräknare behöver du
inte ta med det led som står inom parentes.
c) 942 − 27 2 = (8836 − 729) = 8107
b) 862 + 57 2 = 10645
d) 3452 − 1452 = 98000
Hypotenusan i kvadrat är 502 = 2500
Summan av kvadraterna på kateterna är 482 + 142 = 2500
Eftersom hypotenusan i kvadrat är lika med summan av kvadraterna på kateterna
stämmer Pythagoras sats.
5506
Hypotenusan i kvadrat är 102 = 100
Summan av kvadraterna på kateterna är 82 + 62 = 100
Pythagoras sats stämmer.
5507
a)
5508
a) 52 = 5 ⋅ 5 = 25
c) 12,52 = 12,5 ⋅12,5 = 156, 25
b) 7,12 = 7,1 ⋅ 7,1 = 50, 41
d) 0,552 = 0,55 ⋅ 0,55 = 0,3025
52 + 62 = 61
 61 ≠ 64 →
82 = 64

Triangeln är inte rätvinklig.
b)
52 + 122 = 169 
 169 = 169 →
132 = 169

Triangeln är rätvinklig.
5509
a) 17 2 = 17 ⋅17 = 289
b) 132 = 13 ⋅13 = 169
c) 17 2 + 132 = 289 + 169 = 458
5510
Se facit och lösningen till uppgift 5504. Kontakta din lärare om du behöver hjälp.
5511
a)
112 + 252 = 746 
 746 < 841
292 = 841

c)
152 + 282 = 1009 

412 = 1681

b)
962 − 702 = 4316 

132 = 3364

d)
1342 − 392 = 16435

1202 = 14400

a)
Hypotenusan i kvadrat är 152 = 225 .
Summan av kvadraterna på kateterna
är 92 + 122 = 225 .
Pythagoras sats stämmer.
c)
Hypotenusan i kvadrat är 292 = 841 .
Summan av kvadraterna på kateterna är
202 + 212 = 841 .
Pythagoras sats stämmer.
5512
4316 > 3364
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
1009 < 1681
16435 > 14400
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5513
5514
b)
Hypotenusan i kvadrat är
12,52 = 156, 25 .
Summan av kvadraterna på kateterna
är 12, 02 + 3,52 = 156, 25 .
Pythagoras sats stämmer.
d)
Hypotenusan i kvadrat är
20,82 = 432, 64 .
Summan av kvadraterna på kateterna är
19, 22 + 8, 02 = 432, 64 .
Pythagoras sats stämmer.
a)
7 2 + 192 = 410 
 410 ≠ 441 →
212 = 441

Triangeln är inte rätvinklig.
c)
92 + 402 = 1681
 1681 = 1681 →
412 = 1681

Triangeln är rätvinklig.
b)
122 + 162 = 400 
 400 = 400 →
202 = 400

Triangeln är rätvinklig.
d)
22 + 22 = 8
 8 ≠ 9 → Triangeln är
32 = 9

inte rätvinklig.
Triangeln är rätvinklig. Det betyder att Pythagoras sats gäller.
Hypotenusan i kvadrat är 1602 = 25600
Lisas resultat ger 1012 + 1282 = 26585
Tommys resultat ger 942 + 1282 = 25220
Anns resultat ger 962 + 1282 = 25600 vilket är lika med hypotenusan i kvadrat.
Svar: Ann har bestämt avståndet korrekt.
5515
Detta kan även visas generellt.
Triangeln är rätvinklig, då gäller att a 2 + b 2 = c 2 .
I uppgiften är a = 4 x, b = 3 x och c = 5 x .
Kvadraten på hypotenusan är
c 2 = (5 x) 2 = 5 x ⋅ 5 x = 25 x 2 .
c
a
Summan av kvadraterna på kateterna är
a 2 + b 2 = (4 x) 2 + (3x) 2 = 16 x 2 + 9 x 2 = 25 x 2 .
b
Vi har alltså att 25 x = 25 x . Det är sant för alla värden på x.
2
2
5516, 5517 Exempel som löses i boken.
5518, 5519, 5520, 5521 Se exemplen 5516 och 5517.
5522, 5523, 5524, 5525 Kontakta din lärare om du
5526, 5527, 5528
behöver mer hjälp med detta.
5529
a)
x 2 + 8 = 17
b)
På de flesta moderna miniräknare
trycker man först
-knappen,
sedan matar man in det tal man
skall bestämma kvadratroten till.
x 2 − 24 = 25
x 2 = 17 − 8 = 9
x 2 = 25 + 24 = 49
x2 = 9
x=3
x 2 = 49
x=7
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5530
5531
a)
a)
15 = x 2 − 10
x 2 = 100 − 64 = 36
x 2 = 25
x=5
x 2 = 36
x=6
x 2 = 6 2 + 82
17 2 = 82 + x 2
x 2 = 17 2 − 82 = 225
x 2 = 100
x = 10
x 2 = 225
x = 15
5533
a)
x 2 − 1 = 49
b)
86 = x 2 − 4
x 2 = 49 + 1 = 50
x 2 = 86 + 4 = 90
x 2 = 50
x ≈ 7, 07
x 2 = 90
x ≈ 9, 47
a) Kvadrater på följande heltal ligger mellan 100 och 200:
11 (112 = 121) , 12 (122 = 144) , 13 (132 = 169) och 14 (142 = 196) .
b) Kvadratrötterna av följande heltal ligger mellan 10 och 20:
121, 144, 169, 196, 225, 256, 289, 324 och 361.
Löses enklast med miniräknare men man kan lösa det genom lite tankearbete. Eftersom
8 ⋅ 8 = 64 < 73 och 9 ⋅ 9 = 81 > 73 måste roten ur 73 vara större än 8 men mindre än 9.
Svar:
5536
b)
x 2 = 36 + 64 = 100
Se facit.
5535
100 = x 2 + 64
x 2 = 15 + 10 = 25
5532
5534
b)
73 ligger mellan 8 och 9.
Sätt in värdet på x i formeln för y.
y = 14 x 
 → y = 14 31 ≈ 77,95 ≈ 78
x = 31 
Svar: Bilens hastighet var 78 km/h.
5537
a) Arean är x2 cm2.
x 2 = 47,5
x ≈ 6,892
Svar: Sidan är 6,89 cm lång.
b) Omkretsen är 4x cm.
4 x = 4 47,5 ≈ 27,57
Svar: Omkretsen är 27,6 cm.
5538, 5539, 5540 Se bokens ledning samt lösningen i facit.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Arean
47,5 cm2
x
x
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5541, 5542 Exempel som löses i boken.
5543
Trianglarna är rätvinkliga. Därför kan Pythagoras sats användas för att lösa uppgifterna.
c) x 2 = 3,12 + 9, 7 2
a) x 2 = 202 + 152
x 2 = 9, 61 + 94, 09 = 103, 7
x 2 = 400 + 225 = 625
x 2 = 103, 7
x 2 = 625
x = 25
b)
x 2 = 12, 02 + 13, 02
x ≈ 10, 2
d)
x 2 = 104, 04 + 104, 04 = 208, 08
x 2 = 144 + 168 = 313
x 2 = 208, 08
x 2 = 313
x ≈ 17, 7
5544
Se facit.
5545
x 2 = 20, 02 + 21, 02
x 2 = 10, 22 + 10, 22
x ≈ 14, 4
x 2 = 400 + 441 = 841
x 2 = 841
x = 29
Svar: Hypotenusan är 29 m lång.
5546
a)
d 2 = 1502 + 802
x 2 = 22500 + 1600 = 28900
x 2 = 28900
x = 170
Svar: Diagonalen är 170 cm lång.
b)
x 2 = 4,12 + 6, 7 2
x 2 = 16,81 + 44,89 = 61, 70
x 2 = 61, 70
x ≈ 7,854
Svar: Diagonalen är 7,9 dm lång.
5547
Se facit. Man går 7 rutor (motsvarar 7 cm) i sidled och 3 rutor vinkelrätt i höjdled för att
komma från A till B.
5548
Det är 90D vinkel mellan rakt norrut och rakt österut.
Avståndet mellan Britta och Anders är x m.
x 2 = 852 + 922 = 15689
x 2 = 15689
x ≈ 125
Svar: Avståndet mellan Britta och Anders är 125 m.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5549
Fågelvägen är det x m till toppen.
x 2 = 12502 + 4202 = 1738900
x 2 = 1738900
x ≈ 1318, 7 ≈ 1320
Svar: Fågelvägen till toppen är 1320 m.
5550
Exempel som löses i boken
5551
a)
b)
5552
x 2 + 4 2 = 52
Det sparar tid och knapptryckningar på
miniräknaren att direkt kunna beräkna till
exempel
7,52 − 2, 7 2 utan att först räkna ut
vad 7,52 − 2, 7 2 är.
För att det skall bli rätt räknat behövs
parenteser runt uttrycket under rottecknet
Tryck alltså
( 7,5 x 2 − 2, 7 x 2 )
c)
x 2 + 122 = 132
x 2 = 52 − 4 2
x 2 = 132 − 122
x = 52 − 4 2
x=3
x = 132 − 122
x=5
Svar: Kateten är 3 cm.
Svar: Kateten är 5 cm.
x 2 + 62 = 102
d)
x 2 + 242 = 252
x 2 = 102 − 62
x 2 = 252 − 242
x = 102 − 62
x=8
x = 252 − 242
x=7
Svar: Kateten är 8 mm.
Svar: Kateten är 3 m.
Sträckan BC är x m.
x 2 + 7202 = 8402
x 2 = 8402 − 7202
x = 8402 − 7202
x ≈ 432, 7 ≈ 430
Svar: Det är 430 m mellan B och C.
5553
Se facit. I en rätvinklig triangel måste det finnas en vinkel som är 90D .
5554
Den okända kateten är x cm.
x 2 + 10 = 26
x = 26 − 10
x=4
Svar: Kateten är 4 cm.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5555
Kortaste vägen mellan två punkter (i ett plan) är en rät linje (fågelvägen), i detta fall
hypotenusan i en rätvinklig triangel med katetlängderna 120 m respektive 40 m.
Tillbakavägen är x m.
Totalt simmar hon (120 + 40 + x) m .
x 2 = 1202 + 402 

x = 1202 + 402  → 120 + 40 + x ≈ 287 ≈ 290

x ≈ 127

Svar: Ingrid simmar 290 m.
5556
Se bokens ledning samt lösningen i facit
5557
Den del av stammen fällts motsvaras av hypotenusan i en rätvinklig triangel med
katetlängderna 1,4 m respektive 14,5 m. Denna del av stammen är x m lång.
Trädet totala höjd var (1, 4 + x) m.
x 2 = 1, 42 + 14,52 

x = 1, 42 + 14,52  → 1, 4 + 14,57 ≈ 16

x ≈ 14,57

Svar: Trädet var 16 m högt.
5558, 5559, 5560 Se bokens ledning samt lösningen i facit.
Kapitel 5.6
Att ha en bra strategi för att lösa problem är viktigt och det gäller inte bara
inom matematikens område. Tag för vana att använda denna stegmetod i så
stor utsträckning som möjligt, det vinner du på i längden.
1. Förstå problemet
2. Gör upp en plan
3. Följ din plan
Kontrollera ditt svar (är det orimligt börjar du om vid steg 2)
5601
Exempel som löses i boken.
5602
Förstå problemet:
Vad frågar man efter?
Vilka fakta finns?
Uppskatta burkens volym:
Burkens volym efterfrågas.
Burkens höjd och burkens rymddiagonal.
30 cm hög och 34 cm rymddiagonal är som en liten hink,
ca 5-8 liter
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
Gör upp en plan:
Tänk:
Det finns en formel för en
cylinders volym V = π r 2 h .
Skriv:
Volymen V: ? cm3
Eftersom burkens radie inte
finns given i problemet
måste den bestämmas på
något sätt.
Höjden h: 30,0 cm
Diagonalen D: 34,0 cm
Diametern d: ? cm
Med hjälp av Pythagoras
sats kan diametern räknas ut
och därmed även radien
(som ju är hälften av
diametern).
D 2 = d 2 + h2
d = D2 − h2
r=
d
=
2
Rita:
D
h
d
D 2 − h2
2
När radien har räknats ut
kan volymen beräknas.
Följ din plan:
Beräkna radien:
Beräkna volymen:
342 − 302
r=
cm = 8 cm
2
V = π r 2 h = π ⋅ 82 ⋅ 30 cm3 ≈ 6032 cm3 ≈ 6, 0 dm3
Kontrollera svaret:
Volymen uppskattades till mellan 5 och 8 liter och beräknades till 6,0 liter. Eftersom det
var god överensstämmelse mellan det uppskattade (förväntade) resultatet och det
beräknade är vi nöjda och behöver inte göra någon ny plan.
5603
Förstå problemet:
Områdets area skall beräknas.
Uppskatta svaret: Halvcirkeln ser ut att vara något mindre än triangeln.
Totalarean bör därför vara mer än för en triangel men mindre än arean för två trianglar.
Gör upp en plan:
Området kan delas in i två delar: en triangel och en halvcirkel .
bh
π r2
A TOTAL = A TRIANGEL + A HALVCIRKEL där A TRIANGEL =
och A HALVCIRKEL =
2
2
För att använda formlerna för triangelns area måste man veta basens och höjdens längd,
för att använda formel för halvcirkelns area måste man veta radien eller diametern.
Triangelns höjd h är lika med halvcirkelns diameter, fås med hjälp av Pythagoras sats.
Följ din plan:
bh 15 ⋅ 8

A TRIANGEL =
cm 2 = 60 cm 2
=


2
2
h = 17 2 − 152 cm = 8 cm → 
2
π r π ⋅ 42
A
cm 2 ≈ 25 cm 2
=
=
 HALVCIRKEL
2
2
A TOTAL = A TRIANGEL + A HALVCIRKEL ≈ 85 cm 2
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
Kontrollera ditt svar:
Den beräknade arean ligger i intervallet 60-120 cm2 som vi förväntade oss.
5604
Förstå problemet:
Beräkna totala arean.
Arean kan delas in enligt figuren till höger.
Resultatuppskattning: Arean är mellan 15h och 25h.
15
(cm)
13
Gör upp en plan:
Det finns en formel för parallelltrapetsets area.
( a + b) h
där a = 15 cm och b = 25 cm (5+15+5)cm
A=
2
Höjden h cm kan beräknas med Pythagoras sats.
13
h
5
15
5
132 = h 2 + 52 → h = 132 − 52
Följ din plan:
h = 132 − 52 cm = 12 cm
(15 + 25) ⋅12
→ A=
cm 2 = 240 cm 2
2
Kontrollera ditt svar:
15h = 180 < 240 < 25h = 300.
Svaret ligger i det intervall vi förväntade oss.
5605
Förstå problemet:
Räkna ut hur lång tid det tar att gå runt fältet.
Camilla går med hastigheten 75 m/min.
Uppskattning av resultatet:
Omkretsen är ca 1 km vilket tar ca en kvart
405
Gör upp en plan:
1.
Räkna ut den sneda sidan x med hjälp av Pythagoras sats.
2.
Räkna ut figurens omkrets (summan av sidlängderna).
s
3.
Räkna ut tiden med formeln t =
v
där t är tid, s är sträcka och v är hastigheten.
Följ din plan:
1.
”Överhänget” på fältets övre kant = triangelns bas = 80
m. x 2 = 1502 + 802 → x = 1502 + 802 = 170 .
2.
3.
Omkretsen är (150 + 405 + 170 + 325) m = 1050 m .
s 1050
min = 14 min
t= =
75
v
Kontrollera ditt svar:
Svaret 14 min stämmer väl med uppskattningen.
5606
Se bokens ledning samt lösningen i facit
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
h
150
325
(m)
x
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5607
Sökt: Burkens volym
Känt: d = 3,00 dm
Mantelarea = 18,0 dm2
Användbara formler:
A MANTEL = 2π rh = π dh 

2

π
d
h
VCYLINDER = π r 2 h =

4 
h
Kombinera ihop formlerna ovan
A
d 18, 0 ⋅ 3, 00
dm3 = 13,5 dm3
→ VCYLINDER = MANTEL =
4
4
d
Svar: Burkens volym är 13,5 dm3.
5608
Den höga, smala burken har radien r och höjden 2h → VHÖG = π r 2 ⋅ 2h = 2π r 2 h .
Den låga, breda burken har radien 2r och höjden h → V LÅG = π (2r ) 2 h = 4π r 2 h .
4π r 2 h är dubbelt så mycket som 2π r 2 h det vill säga
den låga burken rymmer dubbelt så mycket sylt som den höga burken.
5609, 5610 Se förklaringen i bokens facit. Kontakta din lärare om du vill ha mer hjälp.
5611, 5612, 5613, 5614, Se bokens ledning samt lösningen i facit
5615, 5616, 5617
Kapitel 5.7
5701
Exempel som löses i boken
5702, 5703, 5704, 5705, 5706, Se facit. Kontakta din lärare om du behöver hjälp.
5707
a) H, M, O, T, U, V, W, X, Y, Å, Ä, Ö (och A)
b) C, D, E, H, I, K, X (och B)
5708, 5709, 5710, 5711, 5712, 5713, 5714 Se facit. Kontakta din lärare om du behöver hjälp.
5715
5716
a)
47
≈ 3, 615
13
c)
55
≈ 0, 618
89
b)
68
≈ 0,883
77
d)
89
≈ 1, 618
55
I en gyllene rektangel är förhållandet mellan långsidan och kortsidan 1,618:1
29, 6 1, 618
≈
= 1, 618 :1 .
Förhållandet mellan Parthenons långsida och kortsida är
18,3
1
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5717
5718
a)
BC 15 1, 25
=
=
= 1, 25 :1
1
AB 12
Æ Ej gyllene rektangel
c)
BC 93
=
≈ 1,899 :1
AB 49
Æ Ej gyllene rektangel
b)
BC 55 1, 618
=
≈
= 1, 618 :1
1
AB 34
Æ Gyllene rektangel
d)
BC 144
=
≈ 1, 618 :1
AB 89
Æ Gyllene rektangel
AB är 1,0 längdenhet.
BM = MF som är 0,5 längdenhet
MP är lika lång som MC
P
A
D
Triangeln MFP är rätvinklig, därför kan
Pythagoras sats användas
r 2 = 1, 02 + 0,52 = 1, 25
B
M
F
C
r = 1, 25
Sträckan MC är 1, 25 längdenheter.
Sträckan BC är 0,5 + 1, 25 längdenheter
BC 0,5 + 1, 25
=
≈ 1, 618 :1
AB
1
dvs det gyllene snittets proportioner.
5719
297
≈ 1, 414 :1 .
210
För att få förhållandet 1,618:1 måste kortsidan bli mindre (eftersom långsidan inte kan
öka i detta fall).
Förhållandet mellan ett A4-arks långsida och kortsida är
Antag att kortsidan skall vara x mm. Då får vi följande ekvation att lösa
297 1, 618
1, 618
=
→ x=
≈ 184
x
1
297
Eftersom kortsidan är 210 mm från början måste man klippa bort
(210−184) mm = 26 mm längs med långsidan.
5720, 5721 Se facit. Kontakta din lärare om du vill diskutera dina resultat.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
Tema: Trigonometri
Vinklar kan mätas med olika enheter. I denna kurs används bara den enhet som
innebär att det är 360D på ett varv.
Den typ av miniräknare som används när man räknar trigonometri kan ställas
in för att kunna användas för olika vinkelenheter.
För att få rätt svar när du räknar de följande uppgifterna är det viktigt att din
räknare är rätt inställd. Du kan testa detta genom att undersöka vad sin 90D blir.
Får du resultatet sin 90° = 1 är din räknare rätt inställd.
1
2
a)
sin v =
motstående katet 35
=
≈ 0,574
hypotenusa
61
b)
cos v =
närliggande katet 50
=
≈ 0,820
hypotenusa
61
c)
tan v =
motstående katet 35
=
= 0, 70
närliggande katet 50
Se facit.
På de flesta moderna miniräknare beräknas sin 35D genom att man
1. först trycker på [sin]-knappen,
2. sedan matar man in 35,
3. därefter trycker man
4.
3
[EXE] (Casio) eller [ENTER] (Texas) eller [=].
Vinkeln v och närliggande katet AB är kända och man frågar efter höjden BC som är en
motstående katet. Problemet löses med hjälp av tangens (tan).
tan v =
motstående katet BC
=
närliggande katet AB
→ BC = AB ⋅ tan v = 18, 2 ⋅ tan 40D ≈ 15,3
Svar: Flaggstången är 15,3 m hög.
4
Vinkeln v och hypotenusan AB är kända och man frågar efter avståndet AC som är en
närliggande katet. Problemet löses med hjälp av cosinus (cos).
närliggande katet AC
cos v =
=
→
hypotenusan
AB
AC = AB ⋅ cos v = 625 ⋅ cos 27D ≈ 557
Svar: Avståndet över viken är 557 m.
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002
Kompletterande lösningsförslag och ledningar, Matematik 3000 kurs A, kapitel 5
5
Vinkeln v och hypotenusan AB är kända och man frågar efter avståndet BC som är en
motståendende katet. Problemet löses med hjälp av sinus (sin).
motstående katet BC
sin v =
=
→
hypotenusan
AB
BC = AB ⋅ sin v = 29 ⋅ sin 32D ≈ 15
Svar: Masten är 15 m hög.
6
Se facit
Om du skall bestämma vinkeln v är då tan v =
7
13
gör du så här
19
Casio (de flesta nya modeller): Tryck [SHIFT][tan](13/19)[EXE]
Texas (de flesta nya modeller): Tryck [2nd][tan](13/19)[ENTER]
8
Vill man beräkna hur stor en vinkel v är och man vet hur lång den motstående kateten och
närliggande katet används inversfunktionen arctan v. På miniräknaren betecknas detta tan-1,
hur man gör beskrivs ovan.
tan v =
motstående katet 1,8
=
→ v = arctan (1,8 / 4, 7) ≈ 21D `
närliggande katet 4, 7
Svar: Vinkeln v är 21D
9
a) Ledning: sin v = 56 / 70
b) Ledning: tan v = 45 / 72
10
a) Ledning: tan v = 20 / 32
b) Ledning: cos v = 28 / 36
© NATIONELLT CENTRUM FÖR FLEXIBELT LÄRANDE, 2002