Kurs 2

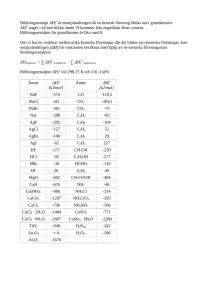
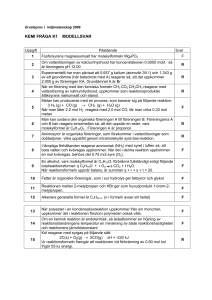
1
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
FY2 Värme
3.9.06
MÅL
Kursens mål är att de studerande skall
• lära sig känna värmefenomen
• kunna undersöka fenomen som hör samman med värmelärans huvudsatser eller ämnens
termodynamiska tillstånd
• bli kapabla att delta i kritiska diskussioner och i beslutsprocesser som gäller miljö och
teknologi.
CENTRALT INNEHÅLL
• gasers tillståndsförändringar och värmeutvidgning
• tryck, hydrostatiskt tryck
• uppvärmning och avkylning av kroppar, fasförändringar och värmeenergi
• mekanisk energi, arbete, effekt och verkningsgrad
• värmelärans huvudsatser, energi i slutna system
• energikällor
2.1. Värmelärans grunder i mekaniken (repetition och fördjupning av grundskolans
fysik)
Arbete och energi
Då en kraft F (enhet 1 newton = 1 N) verkar på en kropp och förflyttare den sträckan s
utförs arbetet W (enhet 1 Nm = 1 joule = 1 J) där då kraftens komponent i förflyttningens
riktning är Fs vi har:
W = Fss
M112
Här är
 Fs/F = cos θ så Fs = Fcos θ
Kinetisk och potentiell energi
Det utförda arbetet kan omvandlas till olika typer av energi såsom potentiell energi:
Ep = mgh
M112
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
2
eller kinetisk energi:
Ek = ½mv2
M112
Det finns andra typer av potentiell energi än den som beror på tyngdkraften, t.ex. den som
är lagrad i en uttöjd eller hoppressad fjäder (mer om detta på kurs 3). Summan av den
kinetiska och potentiella energin är den totala mekaniska energin.
Effekt
P = W/t, P = Fv
M112
Det arbete som utförs eller den energi som omvandlas per tid beskrivs med effekten.
Enheten för effekten P är 1 watt = 1 W = 1 J/s. Vi har att
 P = W/t = F(s/t) = Fv
Notera att denna kraft inte är resultanten, den som används i Newtons II lag F = ma, utan
exempelvis den kraft som lokomotivet i ett tåg ger, och vilken vid konstant hastighet
balanserar motkrafterna i form av luftmotstånd och friktion.
Verkningsgrad
 = Ea/E0 = Pa/P0
M112
Av dessa index anger a den "användbara" energi eller effekt som fås då den med indexet
0 angivna ges in. Vilken effekt eller energi som är "användbar" beror på vad apparaten
används till; för en glödlampa är ljusenergin önskad och värmeenergin kanske ett spill,
men för en brödrost är det tvärtom
2.2. Värmeenergi och temperatur (FY5 s. 8-15, 58, 68-69 mm.)
Materiens aggregationstillstånd:
 fast form (kristallin eller amorf)
 vätska
 gas
 plasma
Materien består av atomer eller molekyler vilka genom "kemiska" (egentligen elektriska)
krafter attraherar eller repellerar varandra.
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
3
I diagrammet ovan är kraften mellan två närliggande atomer (i ett fast ämne eller en
vätska) repulsiv om avståndet mellan dem är mindre än r0, attraktiv på större avstånd. Vid
detta avstånd är totalkraften noll. Den potentiella energin har då ett minimum och om
atomerna har någon kinetisk energi kommer de att vibrerar omkring detta läge som en
massa på en spiralfjäder eller en kula som rullar omkring i en skål. För en enskild atom
kommer dess totala energi ibland att vara rent potentiell, ibland rent kinetisk, för det
mesta en kombination av båda. Vibrationen dämpas inte av luftmotstånd eller friktion!
Temperatur, inre energi och flöde av värmeenergi
Ju större mekanisk energi en atom har, desto "häftigare" vibrerar den omkring
jämviktsläget. Man kan räkna som om all energin var kinetisk (det är inte sant samtidigt
för alla atomer i ett stycke materia).
Låt oss anta att vi har en liten bit glödhet metall, kanske ett mynt upphettat i en gaslåga,
och slänger det i ett badkar fullt av kallt vatten. Vi måste då särskilja mellan tre begrepp:
1. Temperatur (temperature)
Denna vanliga storhet är proportionell mot atomernas genomsnittliga kinetiska
energi. De exakta relationerna kan vara komplicerade; för idela enatomiga gaser (se
senare) är den Ek,medel = (3/2)kT där k = Boltzmanns konstant och T = temperaturen i
enheten kelvin.
(Temperaturenheter: 0 oC = 273 K)
2. Inre energi (internal energy)
Detta är summan av energierna för de enskilda atomerna, vilket blir U = (3/2)NkT där N
= antalet atomer. Notera att den inre energin kan vara vara större hos badkaret med kallt
vatten än det heta myntet, ungefär som invånarna i Kina tillsammans kan en större
inkomst än finländarna, även om finländarnas genomsnittliga inkomst är högre.
3. Flöde av värmeenergi (heat)
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
4
När två föremål eller system (här metallen och vattnet) kommer i kontakt med varandra
kommer atomerna att kollidera med varandra i elastiska kollisioner där den totala
kinetiska energin bevaras. I genomsnitt kommer en atom som rör sig snabbare än den
andra före kollisionen att röra sig långsammare efter, och vice versa. Detta leder till att
den genomsnittliga kinetiska energin (= temperaturen!!!) hos metallatomerna minskar
och hos vattenmolekylerna ökar.
Värmeenergin flödar alltid från ett system med högre energi till ett med lägre. Om två
system har samma temperatur är de i termodynamisk jämvikt. "Värmelärans nollte
huvudsats": att två kroppar har samma temperatur är ekvivalent med att inget flöde av
värmeenergi finns mellan dem.
2.3. Transport av värmeenergi (FY5 s. 40, 92 mm)
Värmeenergi kan transporteras på följande sätt:
1. Ledning (conduction)
När två föremål är i kontakt med varandra som ovan, eller inom ett föremål som när en
metallstång vars ena ände är i elden blir het också i andra änden. Transporten av energi
sker genom kollisioner mellan atomer/molekyler.
Q = λAΔTt / d
M115
där Q = mängden transporterad värmeenergi, λ = värmekonduktivitet i enheten W/mK
(M76-77) , ΔT = temperaturskillnad, t = tid, d = den sträcka värmet skall ledas genom
materialet (tjocklek av fönster, längd av grillspett).
2. Strömning (convection)
Här transporteras själva det heta (eller kalla) materialet, exempelvis när vatten hettas upp
i en värmepanna i källaren och sedan leds genom rör till andra delar av bostaden.
3. Strålning (radiation)
Värmeenergi kan även strålas ut som elektromagnetisk strålning - ljus, infraröd strålning
eller annat - utan att föremål flyttas eller är i kontakt med varandra. Exempel: Solen
värmer planeter genom ljus som flödar genom tomma rymden.
För strålning (svartkroppsstrålning) gäller Stefan-Boltzmanns lag
I = σT4
M121
där I = intensiteten = P/A, effekt som utstrålas per area och  = Stefan-Boltzmanns
konstant = 5.67 x 10-8 Wm-2K-4 , T = temperaturen i kelvin. Formeln kan också skrivas
som P = σAT4. Faktorn A förklarar varför man t.ex. har kylflänsar som ökar den
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
5
värmestrålande ytan på motorcykelmotorer, eller varför djur i arktiska regioner är stora
(förhållandet yta/kroppsvolym mindre, eller varför den afrikanska elefanten har stora
öron). För andra kroppar än svartkroppar gäller att
P = eσAT4
M-
där e = emissivitet, ett dimensionslöst tal som är 1 för svartkroppar, mellan 0 och 1 för
övriga. Samma formel gäller emission och absorption av strålning (Albedo = 1 - e )
4. Avkylning genom avdunstning (evaporative cooling).
Temperaturen är ett mått på den genomsnittliga kinetiska energin för atomerna i ett
stycke materia. Den kan fördelas på de enskilda atomerna enligt Maxwell-Boltzmannfördelningen:
Kurvans topp är den mest sannoliga hastigheten eller kinetiska energin, medan
medelvärdet är något högre eftersom kurvan är osymmetrisk, högre åt höger. Ju högre
temperatur, desto starkare asymmetri. De snabbaste atomerna/molekylerna kan i vissa fall
lämna materialet, exempel: Vattnet i ett dricksglas som lämnas fram flere veckor
avdunstar även om temperaturen inte är 100 grader C.
2.4. Värmeutvidgning (FY5 s. 35-38)
Grafen av potentiell energi som funktion av separation mellan atomer är vanligen
asymmetrisk så att den stiger brantare mot mindre separation. Då temperaturen ökar har
atomerna mer kinetisk energi och vibrerar "högre upp" på kurvan; asymmetrin gör att de
då i genomsnitt är längre från varandra. Därför utvidgas de flesta material vid
upphettning. Undantag är vatten som minskar i volym då det värms från fryspunkten till
ca 4 grader Celsius, varefter det igen utvidgas.
För längdutvidgning gäller då α = längdutvidgningskoefficienten att
l = l0(1 + t)
M115
6
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
Typiska längdutvidgningskoefficienter (M72-77):
järn 11.7 x 10-6 K-1
koppar 16.8 x 10-6 K-1
silver 19.2 x 10-6 K-1
För area- och volymutvidgning kan motsvarande samband skrivas.
A = A0(1 + βt)
M-
och
V = V0(1 + t)
M115
Approximativt gäller för area- och volymutvidgningskoefficienterna
β ≈ 2
 ≈ 3
M-
Några typiska värden (M78-79): etanol 1.1 x 10-3 K-1 vatten 0.21 x 10-3 K-1 (ej konstant).
2.5. Värmekapacitet och specifik värmekapacitet (FY5 s. 72-80)
Då en mängd värmeenergi Q (enhet J) tillförs eller avges från ett föremål med massan m
är dess förändring i temperatur Δt. Beroende på materialet har vi olika värden på c = den
specifika värmekapaciteten:
Q = cmt
M115
Typiska värden (M72-79):
Järn 0.45 kJkg-1K-1, silver 0.235 kJkg-1K-1, vatten 4.19 kJkg-1K-1 , is 2.09 4.19 kJkg-1K-1
(notera att samma ämne har olika c-värden beroende på aggregationstillstånd!). Med
hjälp av värmekapaciteten C där
C = cm
M115
kan vi skriva Q = CΔt, en formel som även är användbar för föremål som består av olika
material. Då is vid en temperatur under smältpunkten tillförs värme i konstant takt fås
följande kurva:
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
7
Notera att kurvan stiger brantare för is än för vatten, eftersom c-värdet är lägre för is. Om
värme tillförs med effekten P = E/t = W/t = Q/t fås att W = Q = cmΔt varför Δt/W =1/cm
dvs temperaturförändringen per mängd tillförd värmeenergi är omvänt proportionell mot
c och m. (I grafen ovan är t = tiden och T = temperaturen).
2.6. Latent värme vid smältning och ångbildning (FY5 s. 81-88)
Då vatten kokar eller is smälter förändras temperaturen inte trots att värmeenergi tillförs.
Den går istället till att omvandla materiens struktur och öka dess inre potentiella energi.
För mängden värmeenergi Q som behövs/avges vid smältning/stelning av materia med
massan m gäller:
Q = sm
M115
och för den som behövs/avges vid kokning/kondensering gäller:
Q = rm
M115
där s = specifikt smältvärme ("Lf = latent heat of fusion", där "fusion" inte syftar på
kärnreaktionen fusion utan sammanföringen av mindre ordnade atomer/molekyler i
vätskeform till strukturen i ett fast ämne) och r = specifikt ångbildningsvärme (Lv =
latent heat of vaporisation). Några värden:
Vatten s = 333 kJkg-1, järn s = 276 kJkg-1; vatten r = 2260 kJkg-1, etanol r = 841 kJkg-1.
2.7. Tryck, densitet och lyftkraft (FY5 s. 16-32) [delar av detta kan sparas till FY4]
Vi skall snart övergå till termodynamiken, den del av värmeläran som sammankopplar
temperaturen i ett system med makroskopiska krafter. Först behöver vi studera en
sammanlänkande storhet, nämligen trycket. För tryck (pressure) p gäller att
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
p = F/A
8
M114
där F = den kraft som verkar vinkelrätt mot ytan A med. Enhet 1 pascal = 1 Pa = 1 N/m2.
Andra enheter: 1 bar = 100 kPa (på väderkartor ofta millibar = mb, ca 1000 mb är
normalt atmosfärtryck). 1 atmosfär = 1 atm = 760 mmHg = 760 torr (efter den italienske
fysikern Torricelli) = 101.325 kPa. I anglosaxiska länder ofta 1 psi (pound per square
inch) = 6895 Pa. Se M70.
Redan tidigare torde densiteten ρ (rho) vara känd som kvoten av ett ämnes massa m och
volym V:
 = m/V
M114
På djupet h under ytan av en vätska med densiteten ρ är det hydrostatiska trycket p
p = hg
M114
där g = tyngdaccelerationen, eftersom:
 en yta A vinkelrätt mot vätskeytan ovanför sig har en vätskekropp med volymen
V = Ah
 dess massa är m = ρV = ρAh och tyngden F = mg = ρAhg
 trycket på A blir då p = F/A = ρAhg/A = ρhg = hρg.
Från detta kan härledas lyftkraften N (noste, nostovoima?) på en i en vätska med
densiteten ρ nedsänkt kropp med volymen V:
N = Vg
M114
Antag att kroppen är formad som ett rätblock med höjden x = h2-h1 och övre = under ytan
A. (Om den har en annan form kan den antas uppbyggd av ett stort antal oändligt smala
rätblock) Vi har då:
 dess volym V = Ax = A(h2-h1), trycket på ovansidan p1 = h1ρg och kraften som
därför verkar nedåt på ovansidan F1 = p1A = h1ρgA
 motsvarande kraft uppåt på undersidan F2 = h2ρgA
 resultantkraftens belopp N = F2-F1 = ρgA(h2-h1) = ρgV = ρVg
Detta kan även uttryckas så att
N = mdeplacementg = Fdeplacement, dvs lyftkraften = tyngdkraften på den undanträngda
(displaced) vätskan.
2.8. Molberäkningar
Antalet gasatomer eller molekyler vi har i ett system, t.ex. i en behållare vi studerar,
påverkar trycket mot väggerna som kommer av kollisioner mellan gaspartiklarna och
väggarnas atomer. För att ta hänsyn till detta används enheten mol, vilken om vi antar att
materien är uppbyggd av atomer och molekyler i hela antal är ett sätt att uttrycka detta
antal:
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME


9
1 par = 2 stycken, 1 dussin = 12 st, 1 tjog = 20 st
1 mol = 6.02 * 1023 st = Avogadros tal = NA.
Antalet atomer eller molekyler i en mol är valt så att massan av en mol räknat i gram
ungefär motsvarar masstalet för en atom (summan av antalet protoner och neutroner i
atomkärnan). Eftersom det finns något olika varianter av atomerna av samma grundämne
(isotoper, med samma antal protoner men olika antal neutroner) och en del
kärnfysikaliska omständigheter som behandlas på kurs 8 inverkar är detta inte exakt sant,
men närmevärden med högre noggrannhet finns i tabellerna. Ungefärligen har vi:
Atom
1
H
12
C
16
O
Massa per mol
1 g/mol
12 g/mol
16 g/mol
Observera att massan per mol vanligen anges i gram, inte SI-grundenheten kilogram Man
kan omvandla t.ex. 12 g/mol = 0.012 kg/mol. För molekyler räknar man ihop den
sammanlagda massan per mol med hänsyn till hur många atomer av varje sort som ingår:
Molekyl
O2
H2O
CO2
Massa per mol
2*16 g/mol
= 32 g/mol = 0.032 kg/mol
(2*1 + 1*16)g/mol
= 18 g/mol = 0.018 kg/mol
(1*12 + 2*16)g/mol
= 44 g/mol = 0.044 kg/mol
För att få reda på hur många mol av ett ämne vi har används formeln
n=m/M
där n = antalet mol, m = massan (i g eller kg) och M = massan per mol (i g/mol eller
kg/mol).
Exempel 1: Hur många mol är 400 g syrgas O2 ?
 n = m / M = (400g) / (32 g/mol) = 12.5 mol
Exempel 2: Hur stor massa har 3.7 mol koldioxid CO2 ?
 n = m / M => m = nM = 3.7 mol * 44 g/mol = 162.8 g = ca 0.16 kg
Förutom det mekaniska arbete och flöde av värmeenergi som vi i fysiken mest fokuserar
på kan tryck, volym och temperatur i en gas även påverkas av om vi låter antalet mol gas
ändra (pumpar in mer gas i behållaren , eller låter lite läcka ut ur den). Dessutom kan det
totala antalet mol gas vi har påverkas av kemiska reaktioner, t.ex. reaktionen

2 H2 + O2 -> 2 H2O
10
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
innebär att vi har 3 molekyler före reaktionen men 2 molekyler efter den. Då har vi också
3 par/dussin/mol moleklyler före, och 2 par/dussin/mol efter den. Antalet mol går ner till
2/3 av vad det var, även om massan av materia inte ändras.
Kemisk tillämpning: Molberäkningar
Med hjälp av molberäkningar kan man få reda på hur mycket av olika ämnen som behövs
för att få en reaktion att ske, eller hur mycket reaktionsprodukter man får. Detta är av
betydelse då man bedömer miljökonsekvenserna av olika fysikalisk-kemiska fenomen
såsom energiproduktion. Som exempel förbränning av naturgas (metan):

CH4 + 2 O2 -> CO2 + 2 H2O
Antag att vi har 1 kg metan och vill veta A) hur mycket koldioxid som bildas, B) hur
mycket vattenånga som bildas och C) hur mycket syre som behövs då denna metan skall
förbrännas.








massorna per mol är enligt tidigare 32 g/mol för O2, 44 g/mol för CO2 och 18
g/mol för H2O. För CH4 fås (1*12 + 4*1)g/mol = 16 g/mol.
1 kg CH4 innebär n = m/M = (1000g)/(16g/mol) = 62.5 mol
enligt reaktionen får vi lika många CO2-molekyler som vi hade CH4-molekyler,
alltså fås även 62.5 mol CO2
massan av detta är m = nM = 62.5 mol * 44 g/mol = 2750 g (A)
enligt reaktionen får vi dubbelt så många H2O som vi hade CH4, alltså här 2 *
62.5 mol = 125 mol H2O.
massan av detta är 125 mol * 18 g/mol = 2250 g (B)
för varje CH4 behövs två molekyler O2 så vi behöver också 2 * 62.5 mol = 125
mol O2
massan av detta är 125 mol * 32 g/mol = 4000 g (C)
Notera att den totala massan före och efter reaktionen här är konstant: 1.00 kg + 4.00 kg
= 2.75 kg + 2.25 kg.
Fysikalisk tillämpning: Molär värmekapacitet
Tidigare har vi använt den specifika värmekapaciteten c = den mängd energi som behövs
för att höja temperaturen för 1 kg av ett ämne med 1 K. Vi kunde även definiera en molär
värmekapacitet cmol = den mängd energi som behövs för att höja temperaturen för 1 mol
av ett ämne med 1 K. Vi får då sambandet cmol = cM och värdena för några vanliga
ämnen visar ett intressant mönster:
Ämne
Aluminium
Bly
Järn
Koppar
c (Jkg-1K-1)
900
128
450
387
M (kgmol-1)
0.027
0.207
0.056
0.064
cmol (Jmol-1K-1)
24.3
26.5
25.2
24.8
11
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
Silver
Guld
Neon
Kvicksilver
Väte
Vatten
Is
Etanol
235
129
1030
140
14240
4190
2090
2430
0.108
0.197
0.020
0.201
0.001
0.018
0.018
0.046
25.4
25.4
20.6
28.1
14.2
75.4
37.6
111.8
För enatomiga metaller i fast form är alltså cmol ungefär 25 Jmol-1K-1. Man kan förstå
detta så att då en viss energi tillförs ett ämne skall den fördelas på dess atomer eller
molekyler så att deras genomsnittliga kinetiska energi ökar med en viss mängd för att
temperaturen, som är ett mått på denna genomsnittliga kinetiska energi skall öka med en
viss mängd.
[Man kan uppskatta storleksordningen för cmol genom att notera (se vidare nedan) den
inre energin för en ideal gas U= 3nRT/2 varför ΔQ = ΔU = cmolnΔT ger cmol = ΔU/nΔT =
1.5nRΔT/nΔT = 1.5R = 1.5 * 8.31 JK-1mol-1 = 12.5 JK-1mol-1]
2.9. Ideala gaslagar och kinetisk gasteori (FY5 s. 39-54)
I den kinetiska gasteorin antas en "ideal" gas bestå av atomer (eller molekyler) som
 uppfyller den klassiska mekanikens lagar
 kolliderar elastiskt (rörelseenergin bevaras) med atomerna kärlets väggar
 är många till antalet och rör sig i slumpmässiga riktningar
 inte signifikant påverkas av yttre krafter (tyngdkraft eller annat)
 gasatomerna växelverkar inte med varandra på ett sätt som påverkar situationen.
De kan kollidera elastiskt, men detta påverkar inte den totala kinetiska energin i
gasen, och hastigheterna antas ändå vara slumpmässiga. Inga kemiska reaktioner
mellan atomerna antas dock förekomma.
 trycket mot kärlets väggar uppkommer genom att gasatomer kolliderar med
väggatomer varvid någon kraft verkar på dessa (NIII: samma i motsatt riktning på
gasatomen); den totala kraften per väggyta = trycket.
Ur dessa antaganden kan härledas (utelämnas här) den ideala gaslagen
pV = nRT
M115,127
där p = tryck, V = volym, n = antalet mol gasatomer eller molekyler, T = temperaturen i
enheten kelvin, R = ideala gaskonstanten = 8.31 JK-1mol-1 (M71).
Om antalet mol är konstant (kärlet läcker inte och vi pumpar inte in mer gas) gäller
pV/T = konstant
vilket i problemlösning ofta skrivs som
M115
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
12
p1V1/T1 = p2V2/T2 = ...
Boyle's lag: konstant temperatur
Då T1 = T2 fås pV = konstant k eller p = k/V vilket i grafer kan beskrivas som
(Kinetisk teori: Konstant temperatur => samma kinetiska energi i medeltal => samma
hastighet. Om volymen ökar blir det i medeltal längre väg att röra sig; då hastigheten är
densamma inträffar kollisioner med väggarna mer sällan och trycket minskar).
Gay-Lussacs lag: konstant tryck
Då p1 = p2 fås att V/T = konstant k eller V = kT vilket ger följande grafer:
Graferna visar att ingen temperatur lägre än - 273oC = 0 K kan uppnås då volymen inte
kan bli negativ.
(Kinetisk teori: Högre temp. => ... => högre medelhastighet => måste öka sträckan
mellan kollisioner med väggen och därmed volymen för att trycket skall vara samma)
Charles' lag: konstant volym
Då V1 = V2 fås p/T = konstant k eller p = kT med följande grafer:
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
13
Då trycket inte kan bli negativt följer samma slutsats som ovan om den lägsta möjliga
temperaturen.
(Kinetisk teori: samma resonemang som ovan, men om volymen inte ökas kommer
istället trycket att göra det).
2.10. Termodynamikens första huvudsats (FY5 s. 70)
Termodynamikens första huvudsats: energi kan inte försvinna eller uppkomma ur intet,
endast omvandlas till/från andra former av energi eller till/från mekaniskt arbete
ΔU = Q + W
M115
där
 W = det mekaniska arbete som utförts på systemet. Positivt om omvärlden utför
arbete på systemet, negativt om systemet utför arbete på omvärlden (i
engelskspråkig litteratur förekommer denna formel som ΔU = Q - W med omvänd
teckenregel för W)
 Q = flödet av värmeenergi till (positivt) eller från (negativt) det
 U = den totala inre energin = summan av partiklarnas kinetiska och potentiella
energier (Kan definieras även på andra sätt). I ett givet ögonblick är denna
fördelad olika för olika partiklar men för varje partikel är den i något ögonblick
enbart kinetisk. Den är därför proportionell mot den genomsnittliga kinetiska
energin, vilken i sin tur är relaterad till temperaturen enligt (för en ideal gas):
U= 3nRT/2
M115
Detta betyder att en ökning/minskning i U innebär en ökning/minskning av temperaturen.
I många praktiska fall sökes dock en situation där U förblir konstant över en längre tid.
Ex. en ångmaskin utför kontinuerligt arbete för att driva fram ett fartyg (W < 0) medan
värme tillförs den genom att bränsle förbränns (Q > 0). Vi kan då få Q + W = 0, dvs.
ingen förändring i U, dvs. ingen förändring i T (annars skulle maskinen snart överhettas
eller bli mycket kall).
2.11. Termodynamiska processer och cykler i pV-diagram (FY5 s. 42,45,47,70 mm)
Isobar process: trycket är konstant
Isokor process: volymen är konstant
14
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
I en isobar process gäller att arbetet W då exempelvis en kolv i en cylinder pressas ut är
 W = Fs men då trycket p = F/A => F = pA fås W = pAs
 enligt figuren är V = As så
W = pV
M-
dvs. det utförda arbetet är arean under grafen, en enkel rektangel. I en isokor process är
V = 0 varför även W = 0.
Isoterm process:
Ur pV = nRT fås p = nRT/V = k/V där k = nRT. Detta beskriver en hyperbel (jfr y = 1/x,
y = 2/x etc) som finns högre upp i diagrammet ju högre den under processen konstanta
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
15
temperaturen är. Arbetet är fortfarande arean under grafen, men för att beräkna den
behövs nu integralkalkyl.
(Integrera nRT/V med V som variabel vilket ger nRTlnV; om volymen ökar från V1 till
V2 blir ytan under grafen nRTlnV2 - nRTlnV1 = nRTln(V2/V1).
Adiabatisk process:
I en sådan sker per definition inget värmeflöde in eller ut ur det betraktade systemet, dvs
Q = 0 i ΔU = Q + W vilket ger ΔU = W. Om systemet utför arbete på omgivningen är W
< 0 och detsamma gäller då ΔU. Då denna storhet i praktiken är proportionell mot
temperaturen måste denna minska. Vid adiabatisk expansion får vi därför en kurva som
hela tiden går mot lägre temperaturhyperbler i diagrammet. Vice versa för adiabatisk
kompression. I tekniska tillämpningar finns ungefärligen adiabatiska processer då de är
väl isolerade eller sker för snabbt för att ett nämnvärt värmeflöde skall hinna ske (ex.
vissa skeden i förbränningsmotorers arbetscykler, se nedan).
2.12. Värmemaskiner och verkningsgrad (FY5 s. 90, 97-103)
I en verklig maskin bör temperatur och tryck över en längre tid hållas inom något rimligt
område, och den fungerar därför genom en kombination av processer (vilka i praktiken
inte är renodlat någon av de 4 förenklade fallen ovan). Då arbetet vid expansion är
negativ och kompression är positivt kommer nettoarbetet att vara ytan inom den slutna
kurva i pV-diagrammet som delprocesserna i maskinens arbetscykel ger. (I princip är W
< 0 då en nyttig maskin utför arbete på något annat).
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
16
En värmemaskin (heat engine) tar in värmet Q1 = QH vid en högtemperatursida (ex. det
exploderande bränslet i en bensinmotors cylinder) och avger avfallsvärmet Q2 = QL vid
en lågtemperatursida (avgaserna, vilka fortfarande är heta jämfört med yttertemperaturen
men kallare än högtemperatursidan). Härvid fås ut det mekaniska arbetet W.
Nettoflödet av värme Qtot = Q1-Q2 och då maskinens temperatur över en längre tid bör
förbli konstant har vi ΔU = 0, varför ΔU = Q + W = 0 så att Q = Qtot = - W. Om vi istället
vill räkna det utförda arbetet positivt ändrar vi förtecken så att Qtot = W.
Verkningsgraden, kvoten mellan det nyttiga arbete eller energi vi får ut och den energi vi
satt in blir alltså W/Q1 eller:
η = (Q1 - Q2) / Q1
M116
där Q1 och Q2 är den värmeenergi som flödar in i maskinen varma ända resp. den som
avges i den kalla.
Olika verkliga maskiner har olika hög verkningsgrad. Genom att minska förlusterna
p.g.a. friktion o.a. kan denna ökas, men man kan visa att den maximala tänkbara
verkningsgraden, den termiska verkningsgraden ("Carnot efficiency") är
ηmax = (T1 - T2) / T1
M116
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
17
där temperaturerna anges i kelvin.
En värmepump (heat pump) eller ett kylskåp fungerar omvänt till en värmemaskin:
genom att tillföra mekaniskt arbete transporteras värmeenergi från en lågtemperatur- till
en högtemperaturreservoar.
2.13. Entropi och termodynamikens andra huvudsats (FY5 s. 89, 91)
Då en isbit läggs i varmt vatten smälter den och vattnet kyls av, den blir inte
större/kallare och vattnet hetare, även om detta skulle vara tillåtet enligt den första
huvudsatsen. För att beskriva hur naturen fungerar behövs alltså ytterligare en sats.
När kallt vatten blandas med varmt förloras information: vi vet inte om 2 liter ljummet
vatten kom från 1 liter kallt och 1 liter varmt, eller 1.5 liter mycket kallt och 0.5 liter
mycket hett vatten. Två temperaturer blir en - vi har förlorat information. Alla naturliga
processer sker på detta sätt, om inte energi tillförs från omgivningen. Detta är ett sätt att
uttrycka entropiprincipen.
När ett kylskåp som varit avstängt länge (vi har rumstemperatur inne i det) sätts på sker
något som ser ut att strid mot entropiprincipen: vi får två olika temperaturer, en kallare
inne i skåpet och en något högre rumstemperatur. Detta är möjligt eftersom denna sats
endast gäller slutna system: elektrisk energi från världen utanför rummet flödar in i
systemet
Kylskåpet är konstruerad av en ingenjör, men motsvarande händer även i naturen: t.ex.
om en ö och havet omkring den har samma temperatur när solen går upp, kommer ön att
värmas upp snabbare än havet omkring; en sjöbris uppkommer. Vädersystem (t.ex. El
Niño) är exempel lokala undantag från värmelärans huvudsats vilka är möjliga p.g.a. att
solenergi strömmar in; motsvarande vädersystem finns även på andra planeter.
Entropin S i sig svår att beräkna, förändringen i den kan behandlas enligt:
ΔS = ΔQ/T
M115
där för smältning och kokning T = den temperatur vid vilket det sker, för uppvärmning
och avkylning medeltemperaturen i K. ΔS är positiv vid ökande entropi (mer
"oordning"), ΔQ är positiv då ett system upptar energi och positiv då den upptas
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
18
Ex. en massa m av kokande vatten vid 373K blandas med samma massa isvatten vid
273K. Vi får 2m vatten av temperaturen 323K; för avsvalningen gäller
medeltemperaturen 348K och för uppvärmningen 298K. Den totala entropiförändringen
blir då
ΔStot = - cm*50K/ 348K + cm*50K / 298K
> 0 som alltid
2.14. Fasdiagram (FY5 s. 60-65)
Om man beskriver ett ämnes tillstånd i en graf med temperatur T på vågrät axel och
trycket p på lodrät noteras först en kokpunktsgraf, ovan om vilken ämnet är i vätskeform
och nedanom vilken det är i gasform (ånga). Vid en trippelpunkt förgrenas kurvan och en
smältpunktsgraf beskriver gränsen mellan fast ämne och vätska. Den del av
kokpunktsgrafen som är till vänster om trippelpunkten utgör sublimeringsgraf.
Kokpunktsgrafen slutar i en kritisk punkt; om temperaturen är högre än dennas kan ämnet
endast existera i gasform. (Endel litteratur definierar ånga som gas vid temperatur lägre
än den kritiska punktens.
2.15. Energikällor
Produktion av värmeenergi, antingen för användning direkt för uppvärmning eller för
användning i värmemaskiner för produktion av elektricitet eller framdrivning av fordon
är ett betydande tekniskt område. Exempel på sådana energikällor är:
- kemisk förbränning av fossila bränslen ss. kol, olja eller naturgas eller förnyelsebara ss.
biomassa
- solenergi
- vindenergi (vanligen ej för värmeenergi)
- kärnenergi (fission och fusion)
Centrala krav på energikällor är renhet och säkerhet.
19
GYMNASIEFYSIKKOMPENDIET 2005: FY2 VÄRME
2.16. Förslag till experiment
1. Psykrometer. Mät temperaturen med torr och fuktad termometer. Tabellen ger relativ
luftfuktighet i %. Pröva även att fukta med etanol! Diskutera resultaten.
Dry Bulb
Dry Bulb Minus Wet Bulb (degrees celsius)
°C
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
1
88
89
89
89
90
90
90
90
91
91
91
91
91
92
92
92
2
77
78
78
79
79
81
81
81
82
82
83
83
83
84
84
84
3
66
67
68
69
70
71
71
72
73
74
74
75
76
76
77
77
4
55
56
58
59
60
61
63
64
65
65
67
67
68
69
69
70
5
44
46
48
50
51
53
54
55
57
58
59
60
61
62
62
63
6
34
36
39
41
42
44
46
47
49
50
53
53
54
55
56
57
7
24
27
29
32
34
36
38
40
41
43
46
46
47
48
49
50
8
15
18
21
22
25
27
30
32
34
36
39
39
40
42
43
44
9
6
9
12
15
18
20
23
25
27
29
32
32
34
36
37
39
10
7
10
13
15
18
20
22
26
26
28
30
31
33
2. Mät och uppskatta värmeförlusteffekten från ett rum i gymnasiet (jfr FY5 s. 95)!
3. Kokande vatten får svalna av i kärl, t.ex. bägare. Temperaturen (T) mäts med t.ex. 30s
mellanrum. Olika faktorer som inverkar på avsvalningen utprövas, t.ex. isolerande
material, aluminiumfolie/svart papper runt bägaren; vattnet kan göras mer tjockflytande
med potatismjöl => konvektionsströmmar hindras, svalnar långsammare.
4. Datorlaboration: En eller flere (t,T) -dataserier analyseras med Excel. Grafer av
(t,dT/dt) och (T, dT/dt) uppgörs och diskuteras.
5. Volymutvidgningskoefficient för etanol och/eller vatten kan bestämmas genom att en
mätflaska (100 ml för etanol, 500 ml för vatten) fylls vid rumstemperatur och får kylas av
i kylskåp/utomhus. Volymskillnaden mäts genom tillförsel med mätpipett eller mätning
av nivåändring och flaskhalsens innerdiameter.
6. Vattnets ångbildningsvärme bestäms genom att det upphettas till kokpunkten med
doppvärmare med känd effekt, och att mängden som förångas under en uppmätt tid
bestäms. Detta kan ske genom vägning eller genom att notera volymskillnaden.
Alternativ: En värmares (gas eller elplatta) nettoeffekt bestäms under antagande att
vattnets ångbildningsvärme är känd.