Kapitel 3 - kunda.nu

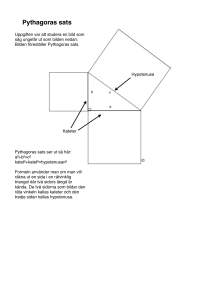
Kap 3 - Geometri
1
GENOMGÅNG 3.1
• Vinklar
Vinklar

     ABC  CBA
Vinklar
Sidovinklar
x  y  180
Sidovinklar
x  180  128  52
Vertikalvinklar
z  v, u  w
Vertikalvinklar
y  z  280
360  280
 40
2
x?
280
180 
 40
2
Alternatvinklar
Linjerna k och
är parallella
wv
l
Likbelägna vinklar
Linjerna k och
är parallella
u v
l
Vinklar
En bisektris är en stråle som delar en vinkel mitt itu.
Konstruktion av bisektris
Trianglar
TRIANGEL
Yttervinkelsatsen (Sidan 167)
Randvinklar och
medelpunktsvinklar (Sidan 170)
Randvinkelsatsen
(Sidan 170)
Följdsatser till randvinkelsatsen
Kan du de här?
Vilka förhållanden visas med dessa bilder?
GENOMGÅNG 3.2
LIKFORMIGHET
Skugga
Det gyllene snittet
ab a
  1, 618...
a
b
TV
16
9
B 16

 1, 78
H 9
TV
Likformighet
3,6 6,0

2,7 4,5
Kontroll med räknare:
3,6/2,7 = 1,33333333333
6,0/4,5 = 1,33333333333
Likformighet
4,5 7,5

2,7 4,5
Kontroll med räknare:
4,5/2,7 = 1,66666666667
7,5/4,5 = 1,66666666667
Likformighet
4,5 7,5

3,6 6,0
Kontroll med räknare:
4,5/3,6 = 1,25
7,5/6,0 = 1,25
Likformighet
Likformighet
Likformighet
x
y
Hur vet vi att trianglarna är likformiga?
Hur långa är sidorna x och y?
Likformighet
x
y
Hur långa är sidorna x och y?
Likformighet
Likformighet
Hur kan man använda likformighet för att
ta reda på hur hög flaggstången är?
(Ingen stege finns i närheten.)
Skugga
~
.
Likformighet
Beräkna sidan DF och vinkeln F om
ΔABC
är likformig med
ΔDEF
45
33
AC  27  19  33
2
2
(27^2+19^2)^(1/2) = 33,0151480384
33 DF
26  33

 DF 
 45
19 26
19
(26 × 33)/19 = 45,1578947368
~
.
Likformighet
Beräkna sidan DF och vinkeln F om
ΔABC
är likformig med
ΔDEF
 A  35  D  35
 F  180  90  35  55
 F  180  (90  35)  55
180-90-35 = 55
180-(90+35) = 55
~
.
Likformighet
Beräkna sträckan x om linjen inuti triangeln är en parallelltransversal.
x
2,8

15,5 4,5
Bakplåtspapper!!!
2,8 15,5
x
4,5
(2,8 × 15,5)/4,5 = 9,64444444444
x  9,6
~
.
Likformighet
~
.
Likformighet
1 2 1 2 2
 
2  22 2
~
.
Likformighet
~
.
Likformighet
A1
A2
A3
A4
A5
A6
=
=
=
=
=
=
594
420
297
210
148
105
x
x
x
x
x
x
841
594
420
297
210
148
mm
mm
mm
mm
mm
mm
Vilka mått har formatet A0?
~
.
Likformighet
A1
A2
A3
A4
A5
A6
=
=
=
=
=
=
594
420
297
210
148
105
x
x
x
x
x
x
841
594
420
297
210
148
mm
mm
mm
mm
mm
mm
Vilka mått har formatet A0?
A0 = 841 x 1189 mm
0,841 1,189  1, 000
[ 0,841 1,189 = 0,999949 ]
Topptriangelsatsen
Topptriangelsatsen talar om för oss att den topptriangel (ADE) som
bildas av en parallelltransversal är likformig med hela triangel (ABC).
Transversalsatsen
AD AE

CD BE
En parallelltransversal (DE) delar två sidor i en triangel i samma
förhållande.
KONGRUENS
KONGRUENS
GENOMGÅNG 3.3
Koordinatgeometri
PYTHAGORAS SATS
https://www.geogebra.org/m/wdQ5VRW9
PYTHAGORAS SATS
PYTHAGORAS SATS
Area = 25 ae
Area = 9 ae
5
3
4
Area = 16 ae
9 16  25
3 4 5
2
2
2
PYTHAGORAS SATS
3 – 4 – 5 = PYTHAGOREISK TALTRIPPEL
PYTHAGORAS SATS
21  42  a
2
a
47
2205
2
a   2205
a  47
2
441  1764  a
2205
a
a
 2205
2
2
441
1764
441 1764  2205
(2205)^(1/2) = 46,9574275275
2
PYTHAGORAS SATS
9  a  23
2
2
2
a  23  9
2
2
a  448
2
a   448
a  21, 2
(448)^(1/2) = 21,1660104885
2
PYTHAGORAS SATS
Hur lång är sträckan x ?
PYTHAGORAS SATS
Hur lång är sträckan x ?
Hur har jag gjort/tänkt här ?
x  13  12
2
x  25
x5
2
FÅGELVÄGEN?
Hur långt är det ”fågelvägen” från A till C ?
AVSTÅNDSFORMELN
2
2
AC

600

400
 
AC  600  400
 AC 
AC  720
2
2
 520000
AC  520000
AC  720
2
Vilket sätt tycker Du
är bäst?
2
AVSTÅNDSFORMELN
Har du sett denna formel förut?
Jo, det är ju Pythagoras sats i lite ny skepnad
HUR LÅNGA ÄR TRIANGELNS SIDOR?
AVSTÅNDSFORMELN
MARKÖR
HÄR!
AVSTÅNDSFORMELN, ÖVN. 1
AVSTÅNDSFORMELN, ÖVN. 2
AVSTÅNDSFORMELN, ÖVN. 3
MITTPUNKTEN
MITTPUNKTEN
MITTPUNKTEN
MITTPUNKTEN
(2,6)
M
(10, 2)
MITTPUNKTFORMELN
(2, 6)
x
2  10 12

6
2
2
y
62 8
 4
2
2
M (6, 4)
(10, 2)
MITTPUNKTFORMELN
(2,6)
x
2  10 12

6
2
2
y
62 8
 4
2
2
M (6, 4)
(10, 2)
MITTPUNKTSFORMELN
3 1 4
x
 2
2
2
3  (3) 0
y
 0
2
2
Mittpunkten är vid (2,0)
MITTPUNKTSFORMELN
y
f(x)=(3/2)x-2
(4, 4)
4
40 4
x
 2
2
2
3
4  (2) 2
y
 1
2
2
2
1
x
-1
1
2
3
4
-1
(0, 2) -2
-3
-4
Mittpunkten är vid (2,1)
MATTEBOKEN
•
•
•
•
•
Avståndsformeln
Randvinkelsatsen
Likformighet och kongruens
Transversaler
Bisektrissatsen
Hjulets radie?
http://www.vaksalaskolan.uppsala.se
Hjulets radie?
Hjulets radie?
Hjulets radie?
Hjulets radie?
Hjulets radie?
Likformighet!
Hjulets radie?
Vilka matematikkunskaper
måste man ha för att kunna
lösa denna uppgift?
•
•
•
•
•
Pythagoras sats
Cirkelns symmetri
Vinklar – alternatvinklar
Likformighet
Något mer?