Termokemi

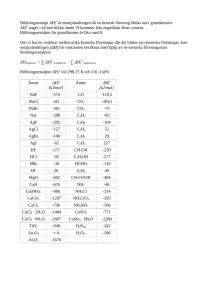
Termokemi
Energi är det viktigaste som finns, utan energi skulle allting bara stå stilla.
Energi förekommer i många olika former, bland annat som rörelseenergi, värmeenergi, lägesenergi,
elektrisk energi och även som kemisk energi.
Vi ska i detta avsnitt titta närmare på kemisk energi …. så klart :)
Egentligen är det solen eller snarare universum som ligger bakom all energi. Alla grundämnen är
resultat av enorma kärnreaktioner i stjärnorna, uppbyggnad av energirika molekyler som
kolhydrater, (sockerarter), sker med hjälp av solljusets energi.
Det som är intressant nu är hur mycket energi vi kan få ur en kemisk reaktion?
Du minns säkert en laboration där du blandade en stålullstuss men en lösning av kopparjoner. Det
som hände var att kopparjonerna tog elektroner ifrån järnatomerna och det bildades fast, rödbrunt
koppar och lösta järnjoner. En så kallad redoxreaktion.
Men du mätte även temperaturändringen under försöket och upptäckte att temperaturen steg, inte
mycket, men ändå, den steg.
Så det fanns alltså energi i kopparjonerna och järnatomerna som de kunde avge till omgivningen
under reaktionens gång.
Man vet till exempel att det krävs energi för att kunna bryta bindningar mellan väteatomer i
vätgasmolekyler, H2.
I följande tabell kan du se hur mycket energi det behövs för att bryta olika typer av bindningar.
Bindning(ämne)
H-H (H2)
H-O (H2O)
H-N (NH3)
H-S (H2S)
H-Cl (HCl)
H-Br (HBr)
H-I (HI)
F-F (F2)
Cl-Cl (Cl2)
Br-Br (Br2)
I-I (I2)
Energi i kJ/mol
436
464
391
364
432
366
298
158
243
193
151
Bindning(ämne)
O=O (O2)
O-Si (SiO2)
NN (N2)
C-C
C=C (C2H4)
CC (C2H2)
C-O
C=O (CO2)
CO (CO)
C-H
Si-H (SiH4)
Energi i kJ/mol
498
466
945
347
598
837
358
805
1077
413
318
På samma sätt som det går åt energi när man bryter bindningar, så får man tillbaka energi när
bindningarna bildas igen.
Det krävs 436 kJ för att bryta samtliga bindningar i en mol vätgasmolekyler, H2, dessa 436 kJ får vi
tillbaka då det bildas en mol vätgas av väteatomer.
Precis som en sten som vi bär upp till översta våning får mer energi, och när vi släpper den utanför
fönstret så återgår den till sitt tidigare energitillstånd.
Om vi tänker oss att vätgas, H2 (g) skall reagera med jod, I2(g), då måste vi först tillföra energi så att
bindningarna mellan väteatomerna och jodatomerna skall brytas.
Men när vi väl har fått fria atomer så kan dessa bilda nya bindningar, fast denna gång mellan en
väteatom och en jodatom så att det bildas vätejodid, HI(g), och då får vi energi tillbaka.
Vi kan då skriva en enkel reaktionsformel:
H2(g)
+
I2(g)
⇌
2HI(g)
Reaktionsformeln kan tolkas så att en mol vätgas reagerar med en mol jodgas och det bildas två mol
vätejodidgas.
För att bryta bindningarna mellan en mol vätgasmolekyler behövs 436 kJ.
För att bryta bindningarna mellan en mol jodmolekyler behövs 151 kJ.
Sammanlagd behövs alltså (436 + 151) kJ = 587 kJ för att bryta samtliga bindningar på
reaktantsidan.
När en mol vätejodidmolekyler bildas får vi tillbaka 298 kJ, eftersom det enligt reaktionsformeln
bildas två mol vätejodidmolekyler får vi alltså 596 kJ tillbaka.
Vi kan då skriva reaktionsformeln på följande sätt:
H2(g)
+
I2(g)
⇌
2HI(g) + 9 kJ
Du ser att vi får mer energi tillbaka än vi tillfogade.
Reaktionen ger alltså 9 kJ för varje mol vätgas som reagerar till vätejodid.
Eller reaktionen ger 9 kJ för varje mol jodgas som reagerar till vätejodid.
Eller reaktionen ger 9 kJ då två mol vätejodidgas bildas ur vätgas och jodgas.
Eller reaktionen ger 4,5 kJ då en mol vätejodidgas bildas ur vätgas och jodgas.
Reaktioner som denna där det bildas ett överskott av energi kallas exoterma reaktioner.
Samtidigt inser du säkert att om vi vänder på reaktionsformeln
⇌
2HI(g) + 9 kJ
H2(g)
+
I2(g)
Reaktioner som använder energi så att produkterna kan bildas kallas endoterma reaktioner.
Man kan säga att en reaktion alltid är exoterm åt ena hållet och endoterm åt det andra hållet.
Övning:
Ta reda på om följande reaktioner är endoterma eller exoterma och beräkna hur mycket energi som
går åt respektive hur mycket energi som frigörs.
H2(g)
+
Cl2(g)
⇌
2HCl(g)
2HBr(g)
⇌
H2(g)
+
Br2(g)
2 H2(g)
+
O2(g)
⇌
2 H2O(g)
Nu har vi tittat på hur mycket energi som går åt eller frigörs då man genomföra en kemisk reaktion.
Nu ska vi istället titta på ämnenas kemiskt bundna energi som omvandlas till värme respektive
värme som omvandlas till ämnenas kemiskt bundna energi.
Denna energi kallas ämnenas ”värmeinnehåll” eller entalpi (grekiska enthalpo = värma).
Entalpi betecknas H och har enheten 1 J.
Man kan inte mäta ämnenas entalpi men däremot kan man mäta entalpiändringen vid en kemisk
reaktion. Till denna mätning används en så kallad kalorimeter.
En kalorimeter är helt enkelt en isolerad behållare som
är
fylld med vatten, en termometer, en omrörare och en
mindre provbehållare för ämnet som skall undersökas.
En viss mängd av ämnet vägs och placeras i
provbehållaren som dessutom är försedd med en plusoch en minusledare. Provbehållaren fylls med ett
överskott av syrgas och försluts. Via en likströmskälla
antänds ämnet tillsammans med syret och den bildade
värmen avges till vattnet vars temperaturändring
bestäms.
Med hjälp av temperaturändringen och ämnets massa kan sedan entalpiändringen beräknas.
Entalpiändringen betecknas  H (delta H) och beräknas enligt:
H   H produkter   H reaktanter
Formeln betyder att delta H är lika med summan av produkternas entalpier minus summan av
reaktanternas entalpier.
Vid en exoterm reaktion avges värme till omgivningen och det innebär att ämnena som reagerar,
(reaktanterna), har större entalpi än ämnena som bildas, (produkterna).
Alltså får  H för en exoterm reaktion ett negativt tecken.
Om vi nu tittar på en av våra tidigare reaktioner
H2(g)
+
⇌
I2(g)
2HI(g) + 9 kJ
så ser vi att reaktionen från vänster till höger är exoterm samt att det frigörs 9 kJ då en mol vätgas
reagerar med en mol jodgas.
Då måste entalpiändringen för reaktionen vara negativ, den är nämligen -9kJ.
Eller kort sagt
H  9kJ
Det betyder alltså att entalpin för vätejodid är lägre än för väte och jod.
Hur bestämmer vi då  H för en kemisk reaktion laborativt?
Om du tittar på försöksuppställningen ovanför så är det både vattnet och apparaturen som värms
upp eller kyls ned under försökets gång. Flytande vattens energiupptagning är det inga problem
J
med, för där vet vi att det behövs cw  4,18 g  K . Det betyder att det behövs 4,18 J för att värma
1,00 g vatten från tex 23,0C till 24,0C.
På samma sätt avger 1,00 g vatten 4,18 J om det kyls från tex 53,0C till 52,0C.
Vill vi då veta hur mycket energi själva apparaturen tar upp så måste vi genomföra några
förberedande försök.
Vi kan nämligen med hjälp av en doppvärmare tillföra en känd energimängd och eftersom vi vet hur
mycket av energin som går åt att värma vattnet så måste resten tagits upp av apparaturen.
Sådana värden kallar man ofta apparatkonstant.
Värmemängden q som utvecklas i en kemisk reaktion bestämmer vi med hjälp av följande formella
samband:
q  c  m  T
Där
q är värmemängden i J
J
c är värmekapaciteten av det ämnet som tar upp energin i g  K
m är massan av det eller de ämnena som värms upp i g
 T är temperaturändringen i K
Om vi tar vår enkla laboration som exempel, så hade vi 20,0 ml = 20,0 g saltsyra i en frigolitbägare,
vi mätte saltsyrans temperatur, tillsatte tex 2,68 g dikaliumkarbonat, K2CO3, och mätte temperaturen
igen. Om vi antar att temperaturändringen,  T var + 4 K, så kan vi beräkna q enligt följande
J
 ( 20,0  2,68) g  4 K
gK
q  379,2 J
q  4,18
Det betyder alltså, om vi låter 2,68 g dikaliumkarbonat reagera med 20,0 g saltsyra,
så är det 22,68 g lösning som värms med 4 K och det motsvarar värmemängden 379 J.
Reaktionsformeln som beskriver det som hände i bägaren ser ut på följande sätt:
K2CO3(s) + 2 HCl(aq)
→
CO2(g) + 2 KCl(aq) + H2O
Om vi nu ökar mängden dikaliumkarbonat till 1,00 mol, dvs. 138,2 g, och samtidigt ökar mängden
saltsyra på motsvarande sätt så borde väl värmemängden som reaktionen producerar också öka!
2,68 g 
2,68 g
 0,01939mol
g
138,2
mol
Värmemängden per mol dikaliumkarbonat, Q i J/mol dikaliumkarbonat blir då:
379,2 J
0,01939mol
J
kJ
Q  19554
 19,55
mol
mol
Q
Det var ju så att temperaturen under försöket ökade, det betyder att värmeinnehållet hos
reaktionsprodukterna är lägre än hos reaktionsreaktanterna.
Då måste alltså entalpiändringen för reaktionen vara negativ. Så entalpiändringen för reaktionen
K2CO3(s) + 2 HCl(aq)
→
CO2(g) + 2 KCl(aq) + H2O
är H  19,55kJ respektive H  19,55
kJ
dikaliumkarbonat
mol
Om vi vänder på reaktionen
→
CO2(g) + 2 KCl(aq) + H2O
K2CO3(s) + 2 HCl(aq)
Så blir entalpiändringen istället
H  19,55kJ
Om vi däremot dubblar den första reaktionen
2 K2CO3(s) + 4 HCl(aq)
→
2 CO2(g) + 4 KCl(aq) + 2 H2O
Så blir entalpiändringen istället
H  39,1kJ
Gör nu samma beräkning fast för ditt eget försök.
I laborationen ”Determination of the enthalpy change for the thermal decomposition of
potassiumhydrogencarbonate” bestämde du temperaturändringen för två reaktioner dels den jag
nämnde precis och dels:
KHCO3(s) + HCl(aq)
→
CO2(g) + KCl(aq) + H2O
Så om du följer samma lösningsväg som beskrivs ovan, så kan du även beräkna entalpiändringen
för reaktionen mellan kaliumvätekarbonat och saltsyra.
Vårt mål är nämligen att beräkna entalpiändringen för en helt annan reaktion, nämligen den
termiska sönderdelningen av Kaliumvätekarbonat enligt:
2 KHCO3(s)
→
CO2(g) + K2CO3(s) + H2O
Frågan är nu hur vi kan med hjälp av vårt försök och våra mätvärden bestämma entalpiändringen
för en helt annan reaktion.
Vi kan börja med att tänka oss två lika stora och lika tunga stenar som ligger utanför skolan på
Östra Köpmangatan, alltså precis utanför skolan.
Om vi tar den ena stenen och bär upp den direkt till D316 där vi lägger den på bordet, så har ju
stenens lägesenergi ökat.
Hur ändras då lägesenergin för den andra stenen om vi tar den och bär omkring den ett tag på stan
innan vi lämnar den på samma ställe som den första stenen?
Samma resonemang gäller kemiska reaktioner, det spelar ingen roll vilka omvägar man tar, bara
man hamnar på samma slutprodukt, så är entalpiändringen lika stor.
Hmm………
Hur kan man då göra om
→
CO2(g) + 2 KCl(aq) + H2O
KHCO3(s) + HCl(aq) →
CO2(g) + KCl(aq) + H2O
K2CO3(s) + 2 HCl(aq)
och
Så det blir
2 KHCO3(s)
→
CO2(g) + K2CO3(s) + H2O
Försök själv genom att använda den röda och den blåa reaktionen, tänk på att du kan vända en
reaktion, du kan multiplicera en reaktion med ett heltal och du kan addera reaktioner.
Inom den analytiska kemin händer det många gånger att det är omöjligt att laborativt bestämma
entalpiändringen för en viss reaktion. Det kan vara olika skäl till det, bland annat att det inte bildas
någon entydig produkt, eller att man inte kan mäta den upptagna värmemängden under reaktionens
gång.
I vårt försök är det så att vi inte kan bestämma hur värmemängd som går åt för att fullständigt
överföra kaliumvätekarbonat till kaliumkarbonat.
Tänk efter hur det i så fall skulle kunna gå till i praktiken.
Ett annat exempel är reaktionen mellan kol och syre så att det bildas kolmonoxid:
2 C(s) + O2(g)
→
2 CO(g)
Reaktionen är inte entydigt, eftersom det även bildas koldioxid då kol och syre reagerar med
varandra.
Alltså kan man inte bestämma entalpiändringen för den nämnda reaktionen
Men  det finns en omväg man kan gå .
Man kan nämligen bestämma entalpiändringen för reaktionen mellan kol och syre då det bildas
koldioxid:
C(s) + O2(g)
→
CO2(g)
Entalpiändringen för reaktionen är H  394kJ
Dessutom kan man bestämma entalpiändringen för reaktionen mellan kolmonoxid och syrgas då det
bildas koldioxid:
2 CO(g) + O2(g) →
2 CO2(g)
Entalpiändringen för reaktionen är H  222kJ
Om vi nu tar den röda reaktionen och multiplicerar allt med 2 så får vi:
då blir H  788kJ
2 C(s) + 2 O2(g) →
2 CO2(g)
Tar vi den blåa reaktionen och vänder den så att reaktanter blir produkter och produkter blir
reaktanter så får vi:
då blir H  222kJ
2 CO2(g)
→
2 CO(g) + O2(g)
Nu kan vi precis som i ett matematiskt ekvationssystem addera reaktanterna i den röda reaktionen
med reaktanterna i den blåa reaktionen och på samma sätt addera produkterna i den röda reaktionen
med produkterna i den blåa reaktionen:
2 C(s) + 2 O2(g) →
2 CO2(g)
→
2 CO2(g)
2 CO(g) + O2(g)
Resultatet blir då:
2 CO2(g) + 2 C(s) + 2 O2(g)
→
2 CO(g) + O2(g) + 2 CO2(g)
Nu har vi 2 mol koldioxid på båda sidor om reaktionspilen och 2 mol syrgas på reaktantsidan och en
mol syrgas på produktsidan. Det betyder att vi kan förkorta i vänster- och högerled:
2 CO2(g) + 2 C(s) + 2 O2(g)
→
2 CO(g) + O2(g) + 2 CO2(g)
Och slutresultatet blir då:
2 C(s) + O2(g) →
2 CO(g)
Vi har alltså, genom att använda oss av matematikens reglar fått fram reaktionen för vilken vi inte
kunde bestämma entalpiändringen.
Eftersom det gick bra att addera reaktionerna så måste det även gå bra att addera
entalpiändringarna:
För den röda reaktionen
För den blåa reaktionen
Summan blir då
H  788kJ
H  222kJ
H  566kJ
Alltså har vi, via en omväg, bestämt entalpiändringen för reaktionen:
 2 C(s) + O2(g)
→
2 CO(g)
H  566kJ 
Följande avsnitt om Gibbs fria energi är hämtat från
http://sv.wikipedia.org/wiki/Gibbs_fria_energi
Gibbs fria energi
Gibbs fria energi, uppkallad efter Josiah Willard Gibbs, är en termodynamisk tillståndsfunktion given av
sambandet:
G = H−TS
där H är entalpi; T temperaturen och S entropin. Både H och S är också tillståndsfunktioner.
Eftersom energi inte har en bestämd nollpunkt används ofta ett uttryck som beskriver förändringen i G.
ΔG = ΔH−TΔS
Gibbs fria energi spelar en mycket stor roll inom kemin. Ett av dess användningsområden är att beskriva olika
reaktioners spontanitet. Eftersom både entalpi-ändringen och entropi-ändringen bidrar till ändringen i Gibbs fria
energi är båda väsentliga för att beskriva reaktioners spontanitet. Det är inte tillräckligt att bara använda entalpiändringen och påstå att den beskriver om reaktioner är spontana eller ej. En reaktion är spontan om värdet för
Gibbs fria energi är negativt, är värdet tvärtom positivt är reaktionen ofördelaktig.
Förändringen i Gibbs fria energi anger det maximala arbetet (energi) som kan utvinnas i en reaktion vid konstant
tryck och temperatur.
Reaktioners spontanitet
En typisk kemisk reaktion kan skrivas:
aA + bB = cC + dD

Om ΔG < 0 betyder det att reaktionen är spontan, den förlöper spontant åt höger.

Om ΔG = 0 betyder det att reaktionen befinner sig vid jämvikt

Om ΔG > 0 betyder det att reaktionen inte är spontan, däremot är reaktionen åt vänster
(bakåtreaktionen) spontan.
Tre (fyra) exempel:
1) Reaktionen nedan (förbränning av kol i syrgas) har ΔH < 0 (exoterm reaktion) och ΔS > 0 (entropin i
systemet ökar). Detta ger att den säkert blir spontan eftersom ΔG får ett negativt bidrag både ifrån
entalpitermen och entropitermen. Reaktionen är spontan vid alla temperaturer.
C(s) + O2(g)
CO2(g)
2) Reaktionen nedan (förgasning av vatten) har ΔH > 0 (endoterm reaktion) och ΔS > 0 (entropin i systemet
ökar). Reaktionen blir spontan då entropitermen dominerar. Reaktionen är spontan vid de temperaturer där
TΔS > ΔH.
H2O(l)
H2O(g)
3) Reaktionen nedan (kondensation av vatten) har ΔH < 0 (exoterm reaktion) och ΔS < 0 (entropin i systemet
minskar). Reaktionen blir spontan då entalpitermen dominerar. Reaktionen är spontan vid de temperaturer
där TΔS < ΔH.
H2O(g)
H2O(l)
4) Ett exempel på spontan reaktion där både ΔH > 0 och ΔS < 0 existerar inte. Ibland kan fotosyntesen
anföras som exempel på motsatsen men det beror bara på att solljuset utelämnas ur det kemiska systemet.