Glimtar ur matematikens historia

Glimtar ur matematikens
historia
HARRY LINDHOLM
Rötterna till den västerländska kulturen kan man till stor del finna i det som greker presterade under den korta perioden 600 till 300 f Kr. Det var då som de konstnärer och författare verkade som blev stilbildande för lång tid framåt. Den europeiska naturvetenskapen uppstod också under denna period.
I denna artikel skall Harry Lindholm redogöra för några av de betydelsefulla
insatser som grekiska matematiker gjorde under periodens första hälft.
1. Miletos (Thales)
2. Samos (Pythagoras)
3. Abdera (Demokritos)
4. Kios (Hippokrates)
5. Athen (Platon)
6. Knidos (Endoxos)
7. Stagira (Aristoteles)
8. Delos
9. Delfi
Ännu för hundra år sedan ansåg man att matematiken nästan uteslutande hade skapats av De
gamle greker. Nu vet vi att de i inte obetydlig
utsträckning hämtade kunskaper och stimulans
från lärde män i Babylonien och Egypten, som
gästfritt tog emot dem och delade med sig av sina
kunskaper om astronomi, matematik och teknik.
Man har spekulerat mycket över orsakerna till
det kulturella uppsving som tog sin början omkring 600 f Kr. En positiv faktor anser man det
ha varit att i de grekiska stadsstaterna spelade vid
denna tid inte prästerna huvudrollen utan klassen
av handelsmän. De första försöken till vetenskaplig forskning — det gällde främst astronomi —
hade visserligen ägt rum i området kring Eufrat
och Tigris, men det var grekiska läkare och
handelsmän som först sökte göra sig fria från
religiösa föreställningar och självständigt behandlade de kunskaper de mottog utifrån.
Den grekiske handelsmannen behövde inte un-
derordna sig åsikterna hos någon härskare eller
något prästerskap. Tack vare sitt yrke och en
verksamhet, som alltmer byggde på att kroppsarbetet utfördes av slavar, fick han en fritid, som
kunde användas till att fundera över vad han såg
omkring sig och diskutera det med jämlikar.
Sönerna till läkare och affärsmän hade råd att
göra studieresor och att lyssna på de män som
blev ryktbara därför att de sökte ge svar på frågor
som: Vad är allt gjort av?, Hur ser jorden ut?,
Vad är liv?
I det politiska livet i dessa stadsstater spelade
förmågan att argumentera en viktig roll. Dialektiken — diskussionskonsten — var därför av stort
intresse för den klass som hade den politiska
makten. Det stora intresse som ägnades matematiken i de grekiska stadsstaterna har delvis sin
förklaring i detta; den betraktades som ett specialområde av dialektiken.
Thales
Han är de förste vetenskapsman som vi vet namnet på. Han föddes och verkade i Miletos, en av
dessa grekiska handelsstäder i västra Mindre
Asien där de s k joniska filosoferna utvecklade
sina tankar. På grundval av vissa uppgifter om
honom, bl a att han skall ha förutsagt en solförmörkelse, som vi vet ägde rum 585, säger man att
han skall ha fötts omkring 624 och dött omkring
546.
Det vi vet om Thales har vi i huvudsak från tre
källor: Herodotos historia om grekerna och omgivande folk skriven omkring 440, Platons dialoger skrivna under några årtionden omkring 360
och utdrag ur Eudemos matematikhistoria
skriven cirka 320, som finns i ett arbete som nyplatonikern Proclos skrev om Euklides första bok
cirka 450 e Kr.
Medan vi från det babyloniska området har
kvar mängder av originalframställningar av matematiska arbeten, till och med lertavlor med skolelevers räkningar, saknar vi med undantag av
några papyrusfragment samtida material om det
antika Greklands matematik.
Från och med Platons tid finns det däremot
avskrifter av avskrifter av avskrifter osv av
många arbeten med matematiskt innehåll. Många
betydelsefulla arbeten före Platons tid och delvis
också efter denna tid har emellertid gått förlorade
därför att de som bestämt vilka papyrusblad som
skulle skrivas av inte ansett att innehållet varit
intressant eller lämpligt att föra vidare.
Thales från Miletos betraktades senare som den
äldste av Greklands sju vise män och det tycks
som om de som följde i hans spår hade en önskan
att tillskriva honom större upptäckter än han
verkligen gjort.
Frimärke med "Babylons hängande trädgårdar".
Efter att i unga år ha skaffat sig en förmögenhet
genom handel med säd och andra jordbruksprodukter skall han ha ägnat sitt senare liv åt resor
och studier. Enligt de nämnda källorna skall han
en tid ha vistats i Egypten och Babylonien. När
han kom hem ägnade han sig bl a åt matematiska
problem. Senare antika matematiker ansåg att
Thales var den förste som sökte bevisa geometriska satser genom en serie av argument och genom
logiska tankesteg. Med andra ord han påstås vara
den som uppfann den deduktiva matematiken,
som 250 år senare fulländades av Euklides.
Enligt vad Proclos säger sig citera från Eudemos skall Thales ha utvecklat de logiska bevisen
för följande satser:
1. En cirkel halveras av sin diameter.
2. I varje likbent triangel är basvinklarna lika
stora.
3. När två räta linjer skär varandra så är
motstående vinklar lika stora.
4. Två trianglar är kongruenta när de har en
sida och två (närliggande) vinklar lika stora.
Men Thales beundrades också för att han löste
praktiska problem. Han skall i Egypten ha väckt
uppmärksamhet genom att beräkna höjden hos
en av pyramiderna med hjälp av dess skugga.
Satsen om kongruenta trianglar skall han ha
använt för att bestämma avståndet från stranden
till ett fartyg till sjöss.
Praktisk matematik
Det finns en rad efterföljare till Thales, som
verkade i städerna på Mindre Asiens västkust och
öarna där utanför, de joniska filosoferna. Dessa
— och i ännu högre grad Platon och hans efterföljare — värderade filosofiska spekulationer
högre än praktiska värv. Detta resulterade i att
grekiska ingenjörers och uppfinnares arbeten ej
uppmärksammades. Det som har skrivits om deras insatser har nästan helt försvunnit.
Ett bevis på hur väl man vid denna tid praktiskt
kunde utnyttja geometriska kunskaper fann man
1882 på ön Samos. En tysk arkeolog, som grävde
efter antika föremål, fann då en 1 km lång
tunnel, som byggts för att leda vatten genom ett
berg. Det visade sig att allt stämde med en beskrivning av ett tunnelbygge som Herodotos lämnat och som enligt honom ägt rum omkring
530 f Kr. Studier av tunneln visade att man
arbetat från båda hållen och att felet då man
möttes var förvånansvärt litet, van der Waerden,
som redogör för detta i sin bok Science awakening, anser att det varit möjligt tack vare att man
redan då hade mycket noggranna vinkelmätningsinstrument, som bl a utnyttjade vattenpass och
kugghjul.
Det fanns fler sådana grundare av religiösa
samfund bland grekerna vid denna tid och i
Indien förde Buddha ungefär samtidigt fram delvis samma idéer som Pythagoras. Liksom denne
omhuldade Buddha matematiken. Framför allt
var det aritmetiken som fick högt anseende inom
buddismen.
Om vi får tro Jamblichos så skall Thales ha
givit Pythagoras rådet att fortsätta sina studier i
astronomi och geometri hos de egyptiska prästerna och från Egypten skall han ha kommit till
Babylonien. Efter att ha vistats där under flera år
kom han hem till Samos för att finna det andliga
klimatet otrevligt sedan Mindre Asien råkat under persisk överhöghet. Han utvandrade därför
till Croton, en av de grekiska kolonierna i södra
Italien. Det bör ha skett år 530 f Kr.
Klotet skall påminna om att man ansåg att Pythagoras var den förste som antog att jorden är ett
klot.
Inte långt från Croton låg den grekiska kolonin
Paestum, vars tempel visar att byggherrarna kunde tillämpa geometri för att uppnå önskade optiska effekter. De höga pelarna gavs sådan lutning
att de syntes vara parallella, då de betraktades
från marken.
Pythagoras tog avstånd från Thales och de
andra joniska filosofernas rationalism och grundade i Croton ett religiöst samfund. Av medlemmarna fordrade han att de skulle föra ett asketiskt liv och att de skulle ägna sig åt vad vi skulle
kalla vidskepliga riter. Han predikade att målet
för människan skulle vara att rena och befria
själen. Ett av medlen som han anvisade var
studier, bland annat av astronomi, matematik
och musik.
Musiken spelade en stor roll för pythagoréerna.
Pythagoras skall ha upptäckt att toner som frambringas av lika spända och lika tjocka strängar,
vars längder förhåller sig som små hela tal, ljuder
vackert tillsammans eller efter varandra. Dessa
iakttagelser fick avgörande betydelse för hans
uppfattning om världen — och speciellt matematiken. De gav honom tanken att hela universum
kan beskrivas med hjälp av de hela talen. Han
tillskrev dem också alla möjliga mystiska egenskaper.
Pythagoras
Bland dem som påstås ha lyssnat till Thales
utläggningar i Miletos nämns den omkring femtio
år yngre Pythagoras. Han föddes och växte upp
på den närbelägna ön Samos.
Det finns en hel del uppgifter om honom i
antika skrifter, bland annat en biografi på latin,
som skrevs av en Pythagorasbeundrare, Jamblichos, omkring 300 e Kr. Enligt dessa bör Pythagoras ha levat från ca 582 f Kr till ca 497 f Kr.
Pythagoras efterföljare, pythagoréerna, betraktade honom som grundare av ett religiöst
samfund och sökte på olika sätt öka hans anseende. Det berättas om underverk som han skall ha
utfört, att han befunnit sig på två platser samtidigt osv. Han skall ha predikat tron på själavandring och att djuren är av samma art som människan och att man därför borde avstå från att äta
kött.
Att tillägna talen mystiska egenskaper var inte
något nytt, men hos Pythagoras utvecklades detta
oerhört. Det var inte bara så att man associerade
talet 1 med en punkt, 2 med en linje, 3 med en yta
och 4 med rymden. Han förband också 2 med
omdöme och manlighet och talet 3 med kvinnlighet; 5 symboliserade äktenskapet osv.
Enligt Pythagoras fanns inget ädlare studium
än det av de hela talen. Pythagoréerna sökte efter
tal med egenartade egenskaper. Tal som man
sökte efter var t ex perfekta tal, dvs tal som är
summan av sina faktorer.
och vänliga tal, dvs talpar där det ena är summan
av alla möjliga faktorer hos det andra.
Man konstruerade också samband mellan tal och
geometriska figurer och med deras hjälp bevisade
men regler för beräkning av talföljders summa.
Man talade om triangeltal (1, 3, 6, 10, . . .),
kvadrattal (1 , 4 , 9, 16, . . . ) , pentagonaltal (1, 5,
12, 22, . . .) osv.
Bild av frimärke med strängaspel.
Det var kanske studiet av strängar som gjorde att
Pythagoras och hans lärjungar ägnade proportionsläran så stor uppmärksamhet. Det är pythagoréerna som infört begreppen aritmetiskt, geometriskt och harmoniskt medium. Beteckningen
harmoniskt medium för 2ab/(a + b) skall ha införts på grund av att pythagoréerna vid försök
med svängande strängar skall ha funnit att då de
gav harmoniska toner så förhöll sig deras längder
som de hela talen 6, 8, 9 och 12. En utförligare
redogörelse lämnar Thorleif Johansen i Forntidens matematik.
Något som också stimulerade talmystiken var
att grekerna utnyttjade det från fenicierna upptagna alfabetet för att beteckna siffror. De använde till att börja med talsymboler som påminner om vad vi kallar romerska siffror, dvs de
använde, förutom det raka strecket för ett, begynnelsebokstäverna i de grekiska orden för fem,
tio, hundra osv.
Under Pythagoras livstid började man använda
de små bokstäverna i alfabetet för att beteckna
tal. Enheterna från 1 t o m 9 fick särskilda tecken
(a, ß osv), likaså tiotalen från 10 t o m 90 (t, x
osv) och hundratalen från 100 t o m 900 (e, Σ
osv). För större tal började man om från början,
men för 1 000 satte man ett litet streck (komma)
framför α.
De grekiska, liksom de egyptiska, symbolerna
för tal var mycket olämpligare än de babyloniska,
då det gällde att göra numeriska beräkningar.
Papyrusblad var också dyrare än lertavlor och
detta kom att påverka den grekiska matematikens
inriktning.
Liksom andra samtida folk använde grekerna
räkneram eller räknebord vid de beräkningar som
gjordes i vardagslivet av t ex affärsmän, byggmästare och skatteindrivare. Hos grekerna kallades en sådan anordning för abax, vilket på latin
blev abacus. Räkningen på räknebordet utfördes
med hjälp av småstenar. Av romarnas namn på
liten sten, calculus, har vi fått orden kalkyl och
kalkylera.
Grekernas användning av bokstäver för att
beteckna tal gjorde också att de inte som babylonierna kunde använda tecken för orden längd,
area och volym för att symbolisera okända storheter.
Dessa olägenheter med det grekiska talsystemet
var en bidragande orsak till att praktiskt taget all
grekisk matematik under denna tid gavs en geometrisk framställning. Men upptäckten av de
irrationella talen var säkert det viktigaste skälet.
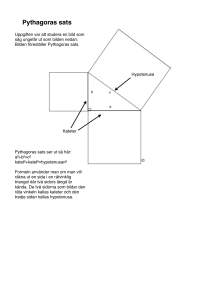
Upptäckten har samband med satsen som bär
Pythagoras namn. I flera antika skrifter anges att
han upptäckt satsen att kvadraten på hypotenusan i en rätvinklig triangel är lika med summan
av kvadraterna på de två kateterna. Detta sam-
band var, som tidigare nämnts, redan känt av
babylonierna omkring 1800 f Kr, men det är
säkert så att det är genom Pythagoras som västerlandet fått kännedom om satsen. Därom är källorna eniga, liksom att han skall ha varit den
förste som givit ett allmängiltigt bevis för satsen.
Hur han bevisade den vet vi emellertid inte.
Pythagoréernas intresse för olika slag av medelvärden kan ha lett dem till att söka svar på
frågan: Vilket är det geometriska medelvärdet av
1 och 2 (dvs med vårt beteckningssätt 1 • 2)?
Denna fråga kunde sedan med hjälp av Pythagoras sats överföras till en fråga om vilket förhållandet är mellan diagonalen och sidan i en kvadrat. Det blev en chock för pythagoréerna då de
fann att förhållandet inte kunde uttryckas med
tal. För grekerna var tal alltid hela, positiva tal.
De uteslöt för övrigt 1 från de egentliga talen och
ansåg det vara både jämnt och udda.
Upptäckten har kanske inte inträffat under
Pythagoras levnad, men i varje fall före 430. Det
bevis pythagoréerna utarbetade är sannolikt det
som återges i den tionde boken av Euklides Elementa, sammanställd omkring 290. Det kan återges så här:
— Om diagonalen AC och sidan AB i kvadraten ABCD är kommensurabla (sammätbara), låt
deras kvot, förkortad så mycket som möjligt,
vara m/n. Av detta följer att
(AC)2/(AB)2 = m 2 n 2 ,
men eftersom (AC)2 = 2(AB)2 leder detta till att
m2 = 2n2,
dvs att m2 är ett jämnt tal. Då måste också m vara
jämnt. Då m/n ej kan förkortas så måste n vara
udda. Men är m jämnt så måste m2 vara delbart
med 4, alltså n2 delbart med 2 och följaktligen n
jämnt. Men då n inte kan vara både jämnt och
udda kan inte AC/AB skrivas som en kvot av
heltal.
Det här givna s k indirekta beviset är det äldsta
bevarade exemplet på ett bevis av detta slag. Som
tidigare nämnts hade babylonierna redan omkring 1700 f Kr beräknat ett approximativt värde
som mycket noggrant satisfierade ekvationen
x2 = 2, men beviset för denna ekvation inte har
någon exakt lösning, som kan anges med rationella tal, var ett betydande matematiskt framsteg.
Längden av en diagonal i en kvadrat med t ex
sidan 1 kunde således inte anges med grekernas
tal. Den var outsägbar, som grekerna uttryckte
det. Vi säger att den anges av ett irrationellt tal.
Däremot kunde man genom en enkel geometrisk
konstruktion åskådliggöra talet. Geometrin ansågs därför vara ett överlägset redskap för en
exakt framställning av matematiken.
Enligt vissa källor skall pythagoréerna ha visat att
5 var outsägbart, innan de visade att det gällde
för 2. Det skall ha skett i samband med studiet
av den regelbundna femhörningen, som skall ha
fascinerat Pythagoras. Med hjälp av diagonalerna konstruerade han femstjärnan, som blev det
tecken som pythagoréerna använde som ett slags
medlemsmärke. Genom ytterligare linjer kunde
han dela upp femhörningen i 30 småtrianglar och
till sin glädje finna att förhållandena mellan vinklarna kunde uttryckas med hjälp av små hela tal.
Vid studiet av sambanden mellan sträckor i figuren skall man så funnit att 5 var ett outsägbart
tal. Andra menar att pythagoréerna visat detta i
samband med sina undersökningar av det gyllene
snittet (Se Nämnaren nr 1, 84/85).
Pythagoréerna studerade sannolikt också förhållandet mellan sidorna hos femhörningar inskrivna i varandra som nedanstående frimärke
visar.
De antika grekiska matematikerna kände troligen till babyloniernas algebra men fann den tydligen inexakt och ej anpassbar till deras siffersystem. De klädde därför algebran i geometrisk
dräkt. Mycket av denna geometriska algebra har
tillskrivits pythagoréerna och det är sannolikt att
många av de satser och bevis för algebraiska
samband som finns i Euklides Elementa kommer
från dem.
Regeln att (a + b){a - b) = a2 - b2 "bevisas" i
nedanstående figur där P är mittpunkt på AB.
Babylonierna löste andragradsekvationer ungefär som vi, medan grekerna använde geometriska
metoder. Anledningen var problemet med de irrationella talen, som var outsägbara, men som
logiskt invändningsfritt kunde tänkas representerade av sträckor.
Ekvationen x2-px + q2 = 0 löstes t ex genom
följande konstruktion, som finns i Euklides Elementa.
Uppgiften är att dela en given sträcka (AB = p)
så att rektangeln, som bildas av dess delar (AQ
och QB), är lika med en given area (q2), där arean
inte får vara större än kvadraten på halva sträckan (dvs q2
(p/2) 2 ).
För att göra detta konstruerar man PC = q på
mittpunktsnormalen till AB. Med C som medelpunkt och PB som radie drar man en cirkelbåge
som skär AB i Q.
Enligt den föregående satsen är AQ • QB =
(PB)2-(PQ)2 men då PB = CQ erhålles med
hjälp av Pythagoras sats att AQ • QB =
(CP)2 = q2.
Om r och 5 är rötterna till andragradsekvationen så gäller att r + s = p och r • s = q2. Men
AQ + QB = p och AQ • QB = q2. Därför representerar AQ och QB rötterna till andragradsekvationen.
Med liknande metoder visade man hur man
skulle geometriskt bestämma de reella lösningarna till andra typer av andragradsekvationer
x2 ± px ± q2 = 0.
Zenon
Det var inte endast de outsägbara talen som
vållade de grekiska matematikerna bekymmer.
Från staden Elea i Syditalien, endast några mil
från Croton, där Pythagoras hade verkat, kom ca
450 f Kr filosofen Zenon till Athen och pekade på
andra svårigheter i det matematiska tänkandet.
Skall man anta att en storhet är oändligt delbar
eller att den består av ett mycket stort antal små
odelbara delar? I sina paradoxer, bl a den om
Akilles och sköldpaddan pekade Zenon på de
logiska problem som båda antagandena ledde till.
En del av svårigheten låg i att man trodde att
summan av ett oändligt antal positiva storheter
måste vara oändligt stor, även om varje storhet
var oerhört liten. Det skulle dröja till 1600-talet
innan man ordentligt studerade konvergenta serier.
Zenons paradoxer, som sedan behandlades utförligt av Aristoteles i hans Logik, verkade mycket stimulerande på det matematiska tänkandet.
Men de svårigheter för tanken som följde med
uttryck som det oändligt lilla och det oändligt
stora eller summan av oändligt många kvantiteter
förde med sig att de grekiska matematikerna
undvek att använda ordet oändligt.
LITTERATUR
utöver den som nämnts i artikeln i Nämnaren
nr 1, 1985/86.
Aaboe, Asger: Antikens matematik från babylonierna till Ptolemaios, Stockholm 1969.
Brun, Viggo: Alt er tall, Matematikkens historiefra oldtid til renessanse, Bergen 1964.
Eves, Howard: An Introduction to the History
of Mathematics, New York 1964.
Newman, James: Sigma, En matematikens
kulturhistoria, Stockholm 1965 del 1 s 27—48,
137—143, 384—387 och del 4 s 1319—1327.