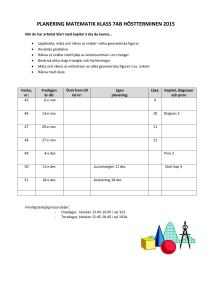
Ett problem från optiken
infallande stråle
y
normal
y"y!x"
F
r"i i
Αr
Α
x
tangent
I figuren ser vi att
vinkelsumman, som ju är
Eftersom
, f år vi
och att
(eller
)
och i den gröna/gråa triangeln får vi
.
Nu kan vi uttrycka
i
. Observera att
är riktningskoefficienten
för den reflekterade linjen. Och denna linje går genom punkterna
och skärningspunkten med kurvan och alltså genom
. Denna linjes riktningskoefficent
är alltså
. Vi får alltså att
och
M.h.a. trigonometri skall vi uttrycka
i
Detta ger nu differentialekvationen med randvillkor
Här behövs ett knep. Sätt
:
,
. Insatt i
ekvationen ovan, där vi bortser fr ån "minus" i " ", f år vi
1
Vi löser dessa integraler.
Vi förenklar och sätter in
. Efter lite algebra får vi
och med
Detta värde på
sätter vi in i samma ekvation
Om lösningen
Att det är en parabel, eller i tre dimensioner, en paraboloid, som reflekterar alla
parallella strålar till ett gemensamt fokus ( ) var känt redan under antiken. På den
tiden fanns inte differential- eller integralkalkylen, utan påståendet visades enbart
m.h.a. geometri. Ovan bevisas dels att
är en lösning, och dels att det är
den enda lösningen. Dessutom får man veta var fokus skall placeras.
En parabolantenn är (en del av) en paraboloid och kan användas såväl som sändare
som mottagare.
F
2
