ovn2.odt - NeoOffice Writer
advertisement

Data och Informationsteknik / Computer Science and Engineering
Chalmers University of Technology and University of Gothenburg
Erland Holmström
Göteborg 24 jan 2014
Övning 2 i Datastrukturer
Inga övningar behöver redovisas men tänk på att jag gillar att knyta an till övningsuppgifter
och labuppgifter på tentan så det kan löna sig att ha gjort (och förstått) dessa.
Jobba gärna i grupp men se till så att alla "hinner med". Det är helt meningslöst att en löser
uppgifterna och alla andra hummar instämmande. Det är mycket bättre om alla funderar en
stund över en uppgift och att ni sedan diskuterar varför ni tänker som ni gör.
Komplexitet behandlas i kap 2.4 i boken samt på OH bilderna.
1. Ordna följande funktioner efter tillväxthastighet n4, logn, nlogn, 4n, 3n3, 100n2+n.
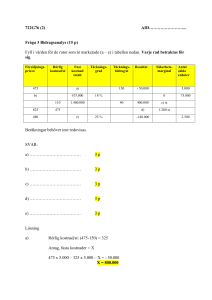
2. Fyll i tabellen nedan. Samla ihop resultaten och beakta dem.
För varje funktion f(n) och tid t skall ni bestämma det största storleken n som kan lösas
under tiden t, där arbetet tar f(n) mikrosekunder. (med log menas här 2-logaritmen). Två
storlekar har redan beräknats, för att ni skall lättare komma igång.
f(n)
1 sekund
log n
~ 10300000
1 timme
1 månad
1 sekel
sqrt( n )
n
n * log n
n2
n3
2n
n!
12
12an beräknades så här: 60 minuter * 60 sekunder * 106 mikrosek. = 3 600 000 000
12! = 479 001 600 < 3 600 000 000 och 13! = 6 227 020 800 > 3 600 000 000
Begrunda också dessa visa ord som beskriver varför en effektiv algoritm alltid är bättre
än en dubbelt så snabb dator:
"Om vi har en O(2n) algoritm som tar en timme på sig att lösa ett problem med 100
indata så tar den 2 timmar för 101 indata!”
3. Antag att du har ett fält med n osorterade tal. Vad är komplexiteten för att
a) ta ut första resp. sista elementet?
b) ta ut det minsta elementet?
c) skriva ut hela fältet?
d) hitta det 5e största elementet?
-1-
2
4. Resonera om komplexiteten för följande kodsnuttar. Räkna först ut antalet operationer
med "handviftning". Skriv sedan ner en summaformel för komplexiteten och lös den.
Ange sedan ordo-funktionen. Antag int n och int a.
// kod 1
for (int i=0; i<n; i=i+1 ) {
a = i;
}
// kod 2
for (int i=0; i<n; i=i+2 ) {
a = i;
}
// kod 3
for (int i=0; i<n*n; i=i+1 ) {
a = i;
}
// kod 4
for (int i=1; i<n; i=2*i ) {
a = i;
}
// kod 5
for (int i=0; i<n; i=i+1 ) {
for (intj =0; j<=n; j =j+1 )
a = i;
}
// kod 6
for (int i=0; i<n; i=i+1 ) {
for (int j=0; j<=i; j=j+1 )
a = i;
}
// kod 8
for (int i=0; i<n*n; i=i+1 ) {
for (int j=0; j<=i; j=j+1 )
a = i;
}
// kod 9
for (int i=0; i<n; i=i+1 ) {
for (int j=0; j<=i; j=j+1 ) {
for (int k=0; k<=j; k=k+1 )
a = i;
}
}
// kod 10
for (int i=1; i<=n; i++ ) {
for (int j=1; j<=2*i; j++ ) {
if ( j%i == 0 ) {
for (int k=1; k<j; k++ )
a = i;
}
}
}
5. Komplexitet och testning: Givet är en mängd S med tal och ett tal x. Beskriv en algoritm
som avgör om det finns två element i S vars summa är exakt x. Algoritmen får ta max
O(n) tid. Antag att mängden lagras i ett sorterat fält. Visa/motivera att algoritmen tar max
O(n) tid.
Använd ett huvudprogram (main) och en metod
boolean check(int[] f, int x)
Om du har ett fält int[] f = {2,4,6,8,....} och anropar med check(f, 10) så skall svaret vara
självdokumenterande och skrivas som
2 8 true ** true, första och 4e talet
där 2 8 är talen vars summa är 10, true är resultatet från check och allt efter ”**” är vad
svaret före ”**” borde vara. (Det räcker naturligtvis inte med en test ... Du måste vara
övertygad om att metoden fungerar)
6. Vad är lösningen på följande summor?
n
a)
∑1
i =1
n
b)
∑i
i =1
n
c)
∑ a⋅x
i =0
n
i
d)
∑ 2i
i =0