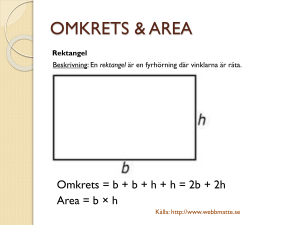
Areans omkrets eller omkretsens area?
advertisement

Malmö högskola Lärarutbildningen Natur – miljö – samhälle Examensarbete 15 högskolepoäng Areans omkrets eller omkretsens area? The circumference of the area or the area of the circumference? Peter Garmfors Kenth Johnsson Lärarexamen 270hp Matematik och lärande Höstterminen 2008 Examinator: Handledare: Leif Karlsson Ange handledare Handledare: Annette Johnsson 2 Sammanfattning I vår studie har vi valt att undersöka i vilken utsträckning eleverna har förståelse för de geometriska begreppen area och omkrets och framförallt om eleverna kan skilja på dessa begrepp. Vi valde att genomföra undersökningen med hjälp av en enkät som besvarades av totalt 152 elever från 8 klasser fördelat på skolår 8 och 9. Enkäten består av rena matematiska uppgifter såväl som textuppgifter för att prova olika infallsvinklar hos våra informanter. Resultatet visar på att det finns brister och svårigheter med att skilja de båda begreppen åt vilket ytterligare förstärker vår egen erfarenhet samt tidigare studier på området. De största problemen uppstår när det gäller att hantera areabegreppet. Vi har en klar uppfattning om att en del av dessa problem kan åtgärdas genom ett förändrat lärande som utsätter eleven för konkret, laborativ och kommunikativ matematik som ställer högre krav på matematisk förståelse. Nyckelord Area, förståelse, geometri, kön, omkrets 3 4 Innehållsförteckning Sammanfattning ................................................................................................................ 3 Nyckelord ................................................................................................................. 3 1 Inledning ........................................................................................................................ 7 1.1 Syfte ........................................................................................................................ 8 1.2 Bakgrund ................................................................................................................ 8 1.3 Litteraturgenomgång .............................................................................................. 9 1.3.1 Definition av begreppen area och omkrets ...................................................... 9 1.3.2 Definition av förståelse .................................................................................. 10 1.4 Frågeställningar .................................................................................................... 15 2 Metod ........................................................................................................................... 16 2.1 Urval ..................................................................................................................... 16 2.2 Datainsamlingsmetod ........................................................................................... 18 2.3 Val av enkätfrågor ................................................................................................ 19 2.4 Procedur ................................................................................................................ 21 2.4.1 Pilotstudie ...................................................................................................... 21 3 Resultat ........................................................................................................................ 22 3.1 Förtydligande av kodning på insamlade enkätsvar............................................... 22 3.1.1 Val av benämning på kön i enkäten............................................................... 22 3.2 Finns det brister i förståelse av begreppen area och omkrets, och i så fall vilka? 23 3.2.1 Resultatanalys av frågorna 5-8 ...................................................................... 23 3.2.2 Resultatanalys och sammanfattning av frågorna 9-11 ................................... 25 3.2.3 Resultatanalys och sammanfattning av frågorna 12-16 ................................. 26 3.3 Vilka resultatmässiga skillnader med avsikt på kön visar undersökningen?........ 28 3.3.1 Resultatanalys och sammanfattning av frågorna 5-8 ..................................... 28 3.3.2 Resultatanalys och sammanfattning av frågorna 9-11 ................................... 29 3.3.3 Resultatanalys och sammanfattning av frågorna 12-16 ................................. 29 3.3.4 Jämförelse av totalpoäng ............................................................................... 30 3.4 På vilket sätt framträder olika resultat beroende av antal år i svensk skola? ....... 30 3.4.1 Resultatanalys och sammanfattning av frågorna 5-8 ..................................... 30 3.4.2 Resultatanalys och sammanfattning av frågorna 9-11 ................................... 30 3.4.3 Resultatanalys och sammanfattning av frågorna 12-16 ................................. 31 3.4.4 Jämförelse av totalpoäng ............................................................................... 31 5 4 Diskussion ................................................................................................................... 32 4.1 Resultatets tillförlitlighet ...................................................................................... 32 4.2 Finns det brister i elevers förståelse av begreppen area och omkrets, och i så fall vilka? .......................................................................................................................... 33 4.3 Vilka resultatmässiga skillnader med avsikt på kön visar undersökningen?........ 36 4.4 På vilket sätt framträder olika resultat beroende av antal år i svensk skola? ....... 37 4.5 Slutsatser............................................................................................................... 39 4.5.1 Egna tankar och reflektioner.......................................................................... 41 4.5.2 Förslag till vidare forskningsfrågor ............................................................... 41 Referenslista ................................................................................................................... 42 Litteraturreferenser ..................................................................................................... 42 Webbreferenser ........................................................................................................... 45 Bilagor ............................................................................................................................ 46 Bilaga 1 - Enkät .............................................................................................................. 46 Bilaga 2 - Föräldrainformation ....................................................................................... 49 6 1 Inledning När vi nu är på sista delen av vår lärarutbildning och har till uppgift att skriva ett examensarbete har fokus landat på ett av de viktigare områdena inom vårt huvudämne matematik, nämligen geometri. När det gäller själva begreppen vi valt att studera är det elevers förståelse kring area och omkrets som undersökningen behandlar. Under utbildningens teoretiska och verksamhetsförlagda tid har det talats en hel del om att den försämrade matematikkunskapen i grundskolan av idag till stor del beror på att inlärningen sker utifrån att lära sig regler inför provet istället för en djupare inlärning som handlar om förståelse och som leder till att ungdomarna kan ta med sig matematiken ut i sin vardag och använda den praktiskt. Framförallt under vår VFT (verksamhetsförlagd tid) har vi själva till stor del upplevt att det gamla traditionella undervisningssättet där läroboken regerar och att det ofta handlar om att räkna snabbt och vara först klar är det stora målet istället för undersökande konkret matematik där eleverna utmanas att kommunicera och tänka matematik. Vår erfarenhet är följaktligen att många elever i grundskolans år 8 och 9 ofta har svårt att skilja på begreppen area och omkrets. Om det är så på de skolor vi valt ut för detta arbete ska vi försöka ta reda på genom att göra en enkätundersökning (se bilaga1). Vi har funnit ett examensarbete från höstterminen 2005 som tar upp en liknande frågeställning - “Elevers förståelse för det matematiska begreppet area” av Lundkvist & Svensson (2005) - som bygger på kvalitativa intervjuer av tio elever i skolår 8. Vår tanke är att jobba vidare på den men att även utveckla med begreppet omkrets och rikta den till skolår 8 och 9. 7 1.1 Syfte Syftet med vårt arbete är att undersöka eventuella skillnader i förståelse kring de geometriska begreppen area och omkrets hos elever i skolår 8 och 9. Kan eleverna säkert skilja på dessa begrepp? Utöver detta kommer vi att inrikta oss på tänkbara resultatmässiga skillnader beroende av kön och antal år i svensk skola. 1.2 Bakgrund Både läroplan och kursplan ska ligga till grund för planering av den undervisning som ska bedrivas i skolan. I läroplan Lpo 94 (Utbildningsdepartementet, 1994), när det är fråga om kunskap, står det att kunskap inte är ett entydigt begrepp. Kunskap kommer till uttryck i olika former - såsom fakta, förståelse, färdighet och förtrogenhet - som förutsätter och samspelar med varandra. Under rubriken “Mål att uppnå i grundskolan” står det att skolan ansvarar för att varje elev efter avslutad grundskola ska behärska grundläggande matematiskt tänkande och kunna tillämpa det i vardagslivet. I kursplanen för matematik (Skolverket, 2000) - Mål att sträva mot - står bland annat att varje elev ska utveckla sin tal- och rumsuppfattning samt grundläggande geometriska begrepp. I målen som eleverna ska ha uppnått i slutet av det nionde skolåret anges att de ska kunna använda metoder, måttsystem och mätinstrument för att jämföra, uppskatta och bestämma längder och areor. Dessutom ska de kunna beskriva viktiga egenskaper hos vanliga geometriska objekt. 8 1.3 Litteraturgenomgång 1.3.1 Definition av begreppen area och omkrets Area Definitionen av area när vi söker ordet i Nationalencyklopedin (2008a) ger följande beskrivning: tidigare yta, mått på en figurs ytinnehåll. Area anges enligt SI (det internationella måttenhetssystemet) i enheten kvadratmeter (m2). Exempel: en triangels area är hälften av basen gånger höjden. I en av grundskolans läroböcker, Matematikboken Grön Y för grundskolans senare del av Lennart Undvall m.fl. (1997) finns ingen egentlig förklaring av vad area är utan fokus ligger på hur arean beräknas på våra vanligaste polygoner, rektangel, kvadrat, parallellogram, romb samt triangel. Exempelvis på rektangeln beskrivs detta genom att istället för längd och bredd säger man ofta bas och höjd vilket ger A = bh. Noterbart är att detta läromedel används på en av de undersökta skolorna. Denna begreppsbildning, att arean är längden multiplicerat med bredden, kan tyckas vara tillräcklig för de flesta elever, att lära sig denna regel. Det har dock visats sig att många elever utifrån denna regel blandar ihop begreppen area och omkrets (Anderberg, 1992). Att mäta arean, storleken av en yta, är mer komplicerat än att mäta en sträcka eftersom man i allmänhet inte direkt kan avläsa ett mätetal. En av anledningarna till att elever blandar ihop omkrets och area kan vara att omkretsen också är ett mått, som är kopplat till ett inneslutet område (Kilborn, 1992). Omkrets Motsvarande beskrivning i NE.se (2008b) för omkrets är: ett föremåls ytterkant i en dimension, vanligen i fråga om mer eller mindre cirkelformat föremål; även motsvarande längd. I det läromedel som angavs i beskrivningen av area blir den kortfattade beskrivningen 9 att omkretsen av en polygon, en månghörning, får man genom att addera längderna av polygonens sidor. Förklaringen av omkrets och area har i denna matematikbok sammanställts på en sida vilket vi menar kan vara något begränsat för dessa viktiga begrepp inom matematiken. 1.3.2 Definition av förståelse Bakgrunden och intresset för vår undersökning kan vi härleda till att vi dels själva upplevt att ett flertal av dagens elever har problem med att skilja på begreppen area och omkrets, dels har det konstaterats i ett antal studier över en längre tid. I detta sammanhang har definitionen av förståelse en central roll eftersom förståelse uppfattas på olika sätt. ”I filosofisk mening innebär det en tolkning av något meningsfullt” (NE.se, 2008c). Kilborn (1992) konstaterar att geometri under några år fört en tynande tillvaro i skolan beroende på en konflikt mellan “förståelse och praktisk färdighet” och “förmågan att bevisa geometriska satser”. Skulden till denna konflikt tillägnas dagens lärare som sägs sakna teoretisk bakgrund i geometri. I en studie av Skemp (1976) beskriver han skillnaderna mellan relationell och instrumentell förståelse. När det gäller relationell förståelse har eleven både kunskap om hur och varför en uppgift löses på ett eller flera sätt i motsats till instrumentell förståelse där eleven strävar efter en regel för att så snabbt som möjligt nå fram till svaret utan att kanske egentligen förstå varför. Han menar att när det gäller lärarens försök till relationell förståelse genom att grundligt förklara, inte bara hur utan även varför, är det många elever som blir otåliga och efterfrågar en regel för att kunna nå fram till svaret på uppgiften och sedan gå vidare till nästa uppgift. Rumsuppfattning och geometri har ett nära samband i det att grundläggande rumsuppfattning är en förutsättning för att kunna orientera sig i rummet och för att lära sig geometri (Ahlström m.fl.,2005). För att öka förståelsen gäller det att skapa kreativa och undersökande aktiviteter, där eleverna ges möjlighet till ett experimenterande och utforskande arbetssätt vilket kommer att leda till bättre förståelse och nya insikter inom geometrin. 10 Det mest använda sättet att introducera en areaenhet är i form av en kvadrat. Detta kan förvisso leda till att eleven lär sig ett förfaringssätt men det kan vara svårt för elevens föreställningar att förstå vad det är som gör att en enhet passar. (Kilpatrick m.fl., 2001) I avhandlingen ”Att äga ” (Nilsson, 2005) visar hans studier av lärarstudenter som arbetar med geometriexempel på att olika typer av laborativa mätningar kan utgöra en viktig grund för att utveckla förståelsen för det tredimensionella rummet. Brandell (1999) gör i sina studier liknande iakttagelser när det gäller de viktigaste aspekterna av innebörden av att lära och förstå matematik. Där förklarar Brandell att det handlar om matematisk mognad. Detta är ingen egenskap som gemene man har utan det är snarare en egenskap som man förvärvar och som kan kopplas till den enskilda individens utvecklingsprocess. Nilsson kommer i sin avhandling fram till slutsatsen att laborationer har en potential att kunna skapa intresse, förståelse och nya insikter i geometri för många elever men det ställer stora krav på läraren. Detta är i sig ingen ny upptäckt utan snarare ytterligare ett belägg för att matematiken bör konkretiseras i mycket högre grad vilket redan poängterades i Åskådningsmatematik (Kruse, 1909). Där beskrivs hur konkretion ska hjälpa eleven att nå förståelse genom konkret material och stoff i högre grad än lärarens förklaringar och struktur vilket på ett bättre sätt leder barnet till upptäckter inom det matematiska området. I samma anda betonades det i boken Den grundläggande matematikundervisningen (Wigforss, 1952) åskådningens roll i undervisningen. Dock med tillägget att han varnade för allt för stora krav på konkretion enligt följande citat: Den yttre åskådningen är emellertid ett medel att komma fram till den inre, till en åskådning i fantasien, till det åskådliga tänkandet. Och kravet på åskådlighet kan leda till överdrift i att visa barnen allt möjligt, som de redan har en klar uppfattning av, medan man försummar att uppöva deras förmåga av åskådligt tänkande. Ej blott vid den yttre åskådningen utan ock vid tänkandet bör man sträva efter självverksamhet från barnens sida . (s. 8) 11 Dahlgren, Fritzén, Sjöström & Wallebäck har i ett kapitel i boken Problemlösning (1991) om reflektioner över klassrumssituationer studerat elever som jobbar med det komplicerade areabegreppet. I sina studier har författarna kommit fram till att det är viktigt för eleven att utgå från sin egen erfarenhet och känna trygghet i problemlösningssituationen. Detta leder till att det får ta tid och det ska löna sig att tänka, påpekas också. Aasa m.fl. (2004) refererar till en översyn av undervisningen i matematik i svensk skola av Utbildningsdepartementet från 1986 där lärarna betonade att flertalet elever har utvecklat en negativ syn på matematik och uppfattar ämnet som ett “pluggämne”. Detta handlar om att eleven före prov läser in några formler som de sedan kan glömma bort. I artikeln Att lära om geometriska kroppar (Littler & Jirotková, 2007) som baseras på ett longitudinellt forskningsprojekt som påbörjades 1993, konstateras att man inte utnyttjar barnens tidiga erfarenhet av tredimensionella kroppar fullt ut när barnen börjar skolan. Istället använder de flesta lärare och läroböcker tvådimensionella former som kvadrat, rektangel, triangel och cirkel för att “dessa är lättare för barnen att känna igen”. På detta viset missar man en viktig del vid skolstarten att barnen fortsätter utveckla kontakten med tredimensionella kroppar som byggklossar, kuber. Ett annat konstaterande i denna studie i samband med klassrumsobservationer i flera länder är att under geometrilektioner förekommer det knappast någon kommunikation mellan lärare och elever. Övervägande handlar det om envägskommunikation där läraren instruerar eleverna. Lärarna är nöjda om eleverna kan namnen på de vanligaste tredimensionella kropparna såsom kub, cylinder och rätblock utan att egentligen kontrollera om de känner till kropparnas egenskaper. Löthman (1992) har bl.a. följt svenska elevers standardprovsresultat för årskurs 8 och årskurs 9, under tiden 1965-1989. Geometriuppgifterna har i dessa studier generellt en lägre lösningsfrekvens än övriga typer av uppgifter. Lösningsfrekvensen på geometriuppgifterna uppgick till ca 35 % medan övriga uppgifter hade en lösningsfrekvens på över 50 %. Löthman bedömer att svårighetsgraden på geometriuppgifter har sjunkit under samma period. 12 Pierre van Hiele har i sin forskning sammanställt en teori om elevers tänkande i geometri vilken till stora delar överensstämmer med Piaget. Båda betonade den enskilda individens olika nivåer. Piaget studerade barns utveckling och van Heile observerade inlärningsprocessen (Hedrén,1992). Sammanhang, där eleverna har möjligheter att utforska, uppfinna och diskutera med sina egna ord, är förmodligen det bästa sättet att hjälpa eleverna att skaffa sig en säker grund i geometri. Att lärarna bidar sin tid, i början accepterar elevernas eget språk och låter eleverna arbeta tillsammans i grupper, där de har stora möjligheter att ge uttryck för sina idéer, kan vara kritiska inslag i den ”formel”, som ger lyckad inlärning i geometri. (Hedrén, 1992, s.35-36) Redan Jean Piaget påvisade historiskt hur matematiska begrepp ofta användes rent instrumentellt utan att det gav upphov till generella reflektioner (Piaget och García, 1989). Piaget gav uttryck för att vara ytterst kritisk till traditionell undervisning och var starkt positiv till de undervisningsformer som inleddes under 1960-talet. I detta sammanhang anknyter Sfard (1991) till dessa teorier i det att hon menar att begrepp kan uppfattas som både en operation eller en struktur. För att exemplifiera detta beskrivs att ett rationellt tal kan ses som ett par av heltal, med andra ord som en struktur, eller som resultatet av en division mellan två heltal, en operation. I likhet med Piaget står den ryske utvecklingspsykologen Lev Vygotskij för det som ofta kallas en konstruktionistisk syn på inlärning och utveckling vilket innebär att barnens kunskap utgör en aktiv process där barnen själva konstruerar sin kunskap. Det som bland annat skiljer Piaget och Vygotskij åt är att Piaget ser det som en fråga om individens samspel med ting och skeenden i omgivningen - en kognitiv konstruktionism - medan Vygotskij står för en social konstruktionism där kunskapen uppfattas som skapad socialt till stor del beroende av språket (Evenshaug & Hallen, 2001). När det gäller könsskillnader visar studier på att flickorna generellt ligger något före pojkarna i språkutveckling. Däremot i traditionella intelligenstest får pojkar bättre resultat på tester som mäter visuell och spatial förmåga och matematiskt tänkande. Det är inga stora skillnader som uppvisas men skillnaderna är tämligen stabila och består under hela livet. Det betonas dock att pojkar och flickor i stort är mer lika än olika varandra (Evenshaug & Hallen, 2001). När det handlar om uppfattningar om kön är de i 13 regel väldigt stereotypa vilket många gånger leder till rent psykologiska skillnader mellan könen. Detta leder ofta till att båda könen ofta väljer att nervärdera kvinnors prestationer genom att välja resonemanget att framgångarna beror av tur eller ihärdighet istället för ren begåvning (Evenshaug & Hallen, 2001). Språkets inverkan på inlärningsförmågan är ytterligare en aspekt vi valt att titta närmare på i vår undersökning där vi dels frågar efter antalet år i svensk skola dels har vi en klar uppfattning om att det skiljer radikalt på de två skolorna vad gäller svensk eller utländsk bakgrund. Att lärandet sker, eller bör ske, i ett kommunikativt sammanhang vittnar satsningar på fortbildning av matematiklärare under 1980-talet. Detta med anledning av att studier visar på att språket spelar en viktig roll för den enskilde individens utveckling av lärande och tänkande i matematik. Dock är det fel att se språket som en förutsättning för tänkandet vilket framkommer exempelvis i problemlösning i geometri, där det till stor del handlar om spatiala lösningar, dvs. ickespråkligt (Engström, 1998). Sättet att tänka i bilder är betydligt äldre än förmågan att tänka med ett språk eller som Peter Gärdenfors, kognitionsforskare i Lund väljer att sammanfatta det i en metafor: ”Språket är bara grädden på tankens tårta” (Gärdenfors, 1997). Oavsett så menar Arne Engström i sin slutsats att en viktig del av lärarutbildningen framledes kommer att vara att utveckla förmågan att föra ett matematiskt samtal med sina elever. Ur litteraturen har vi funnit en mängd olika definitioner av förståelse. Läroplanen och kursplanen anger riktlinjer och mål för hur matematikundervisning ska bedrivas. Vår tolkning av detta är att eleverna ska ges möjlighet att behärska matematiska situationer i vardagslivet. Mot bakgrund av vår tolkning så krävs förståelse. Den definition av förståelse som Skemp (1976) beskriver som relationell förståelse är den definition som bäst passar in med vår uppfattning om vad matematisk förståelse är. Det är relationell förståelse som definieras som förståelse i denna studie. 14 1.4 Frågeställningar Mot bakgrund av vårt syfte och den teoretiska litteraturgenomgången har vi för avsikt att söka svar på följande frågeställningar: Finns det brister i elevers förståelse av begreppen area och omkrets, och i så fall vilka? Vilka resultatmässiga skillnader med avsikt på kön visar undersökningen? På vilket sätt framträder olika resultat beroende av antal år i svensk skola? 15 2 Metod Metodavsnittet har vi valt att utforma enligt den struktur som Johansson & Svedner (2006) förespråkar. De anser att underrubrikerna urval, datainsamling och procedur ska ge goda grunder för metodavsnittet och ge det den centrala del som ett vetenskapligt arbete kräver. Vi redovisar vilken urvalsgrupp vi valt och varför vi ansåg den intressant att undersöka. Den vetenskapliga metod vi använt oss av tas upp i delen datainsamling. Det praktiska tillvägagångssättet för vår valda metod redovisas också. 2.1 Urval Urvalets storlek är en av de första frågorna man ställer sig vid användandet av enkätmetoden. Trost (2007) menar att frågan om urvalets storlek är relevant men också samtidigt omöjligt att besvara på ett helt rättvisande sätt. Han gör en jämförelse med att singla slant vilket innebär att ju fler gånger en krona kastas desto närmare en 50/50 fördelning, mellan krona och klave, kommer man. I termer av en undersökning skulle resonemanget då ges av att ju större det undersökta urvalet är desto större är sannolikheten för att få ett material som kan representera populationen. Trost (2007) påpekar att man måste ta hänsyn till ett flertal praktiska aspekter vid val av urvalets omfattning i förhållande till populationen. Han nämner kostnader och tid som några viktiga faktorer men även behovet av undersökningens precisionsgrad. I vårt fall måste vi begränsa antalet enkäter till en, för oss, kostnadsmässigt rimlig nivå. För att höja validiteten skulle ett större urval varit till undersökningens fördel. Kostnaden för utskrifter av enkäter är en faktor som begränsar urvalets omfång. Tidsmässigt skulle den största skillnaden, mellan en liten och stor urvalsgrupp, vara utskick/insamling och sammanställning av enkäterna. Med avseende på undersökningens precisionsgrad så begränsas denna i vårt fall till praktiska omständigheter. Då vi båda författare av detta examensarbete studerar på lärarutbildningen med inriktning mot grundskolans senare del, kändes det mest naturligt att göra en undersökning med några av dessa årskurser som urval. Anledningen är att vi båda tyckte att frågeställningen kändes relevant med avseende på årskurs. Vi har båda också 16 goda kontakter med matematiklärare som undervisar elever i skolåren åtta och nio vilket underlättar tillgången på informanter. I egenskap av informanter valde vi elever från fyra klasser i skolår åtta och fyra klasser i skolår nio. Dessa åtta klasser var jämnt fördelade på två olika skolor med avseende på skolår. De utvalda skolorna skiljer sig väsentligt från varandra. Den ena ligger i en invandrartät stadsdel i en storstad. Arbetslösheten bland elevernas föräldrar är högre än riksgenomsnittet och eleverna har i väldigt hög grad annat modersmål än svenska. Den andra valda skolan ligger i en av kranskommunerna till ovan nämnda storstad. Området anses välbärgat och medelinkomsten för invånarna i kommunen tillhör de högre i Sverige. Elever med annat modersmål än svenska är sällsynta. I vårt urval fanns 38 elever i skolår 8 respektive 36 elever i skolår 9 från en storstadsskola. Antalet elever från skolan i kranskommunen var 31 elever i skolår 8 respektive 47 elever i skolår 9. Det totala antalet elever från de båda skolorna uppgick således till 152. Läroböckerna som används av storstadsskolan är Matte Direkt år 8 (Carlsson, Synnöve m.fl., 2002) respektive Matte Direkt år 9 (Carlsson, Synnöve m.fl., 2003). Upplägget av läroboken följs förhållandevis strikt, vilket går ut på att eleverna själva räknar uppgifterna i läroboken varvat med genomgångar från läraren. På skolan belägen i kranskommunen används läroböckerna Matematikboken Grön/Röd Y (Undvall m.fl. 1996) för skolår 8 respektive Matematikboken Grön/Röd Z (Undvall m.fl. 1996) för skolår 9. Här arbetar man på motsvarande sätt som i storstadsskolan. Med avseende på det externa bortfallet i urvalsgruppen består detta av de personer som vid tillfället för enkätutlämning, tillika insamling, är sjuka eller frånvarande av någon annan anledning (Patel & Davidsson, 2003). I vår undersökning uppgick detta bortfall till totalt 13 elever vilket utgör knappt 8 % av det totala antalet elever som ingick i klasserna. Det interna bortfallet, enligt Patel & Davidsson (2003), består av ofullständigt ifyllda enkäter. I vår undersökning utgörs det interna bortfallet av tre elever från storstadsskolan. Fördelningen mellan könen var två flickor och en pojke. Dessa elever utgör 1,8 % av det totala antalet elever. Om bortfallet uppgår till över 20% 17 bör en särskild analys utföras som tydliggör orsakerna (Patel & Davidsson, 2003). Då vårt bortfall totalt uppgår till cirka 10 % anser vi inte att det totala bortfallet har någon större påverkan på resultatet av vår undersökning. 2.2 Datainsamlingsmetod Enligt Johansson & Svedner (2006) är de vanligaste och lämpligaste datainsamlingsmetoderna vid examensarbete på lärarutbildningen följande: Enkät Kvalitativ intervju Observation Textanalys I vår undersökning ville vi ta reda på elevernas förståelse rörande de matematiska begreppen area och omkrets för olika figurer, kända för eleverna. Dessutom var vi intresserade av eventuella samband med olika bakgrundsfaktorer såsom ålder, aktuellt skolår, kön samt antal år i svensk grundskola. Johansson & Svedner (2006) menar att metoden med enkäter passar bäst om man har för avsikt att undersöka samband mellan det man vill undersöka, i vårt fall förståelse om begreppen omkrets och area, och fakta såsom ålder, kön, utbildning, erfarenheter o.s.v. Med stöd av Johansson & Svedner (2006) ansåg vi att en lämplig datainsamlingsmetod, med hänsyn till våra frågeställningar, skulle vara enkätmetoden. Vid användandet av enkätmetoden bör särskilt stor omsorg läggas vid val och utformning av enkätfrågor. Syftet med våra frågor till informanterna skall vara att kunna ge underlag för svar till undersökningens frågeställning. Varje enkätfråga bör således inneha relevans för att ge nytta för frågeställningen annars bör den tolkas som överflödig. Antal enkätfrågor är också av stor betydelse för en lyckad enkät. I en alltför kort enkät skulle informanterna i vår undersökning ges mindre möjlighet att bedömas rättvist. Det optimala torde då vara en lång enkät med många frågor. Att beakta är emellertid följande: en enkät får inte bli långtråkig och ska kunna besvaras inom rimlig tid. Vår enkät tar tid i anspråk av såväl informanter d.v.s. elever men också dess lärare. Tidsåtgången bör därför vara inom rimliga gränser. Enligt Patel & Davidsson (2003) är det särskilt viktigt att inte ha för många frågor då man använder sig av enkäter som datainsamlingsmetod. De antyder att 18 det kan leda till att man tröttar ut personerna som svarar på dem vilket kan medföra att de inte svarar alls på frågorna. I vår enkät har vi försökt tolka dessa råd så att de passar våra informanter och dess respektive lärare. Enkätens tydlighet med avseende på layout och val av språk är också en viktig aspekt vid en enkätutformning. Vi har försökt att utforma enkätens layout på ett neutralt sätt. Informanterna ska inte luras till ett visst alternativ genom att göra detta mer tillgängligt. Vi anser att språket, med val av t.ex. objekt och konkreta ting, är på en nivå som informanterna behärskar i stor utsträckning. Trost (2007) upplyser om vikten av att använda vanligt och lättförståeligt språk vid utformning av enkätfrågor. Han belyser också vikten av att avstå från negationer och långa frågeformuleringar. Huvudargumentet är att frågorna då kan feltolkas och således ge felaktiga svar på det som egentligen var avsikten med frågan. En fråga ska enligt Trost (2007) innehålla just bara en fråga och inte flera frågor i en. Johansson & Svender (2006) upplyser om många, liknande Trosts, råd med avseende på enkätutformning vid examensarbete: Undvika att utforma enkäter med större omfattning än tre sidor Sträva efter att formulera frågor med fasta svarsalternativ I möjlig grad undvika frågor med öppna svar Endast fråga efter en sak i varje fråga Använda vanligt språk och inte använda ord med luddig betydelse Sträva efter enkätfrågor vars utformning är kortare än 20 ord. Göra förförsök, dvs. pilotstudie 2.3 Val av enkätfrågor Vår enkät (Bilaga 1) är indelad i fyra olika delar. De olika delarna skiljer sig med avseende på vilken typ av information som söks samt på vilket sätt frågorna är utformade. I den första delen av enkäten ville vi få reda på bakgrundsinformation samt åsikter om matematik från respektive informant. I enlighet med Humanistisksamhällsvetenskapliga forskningsrådet (1996), är samtliga frågor anonyma för att inte 19 kunna röja informanternas identitet. Ur den färdiga undersökningen kommer det således inte vara möjligt att identifiera informanterna liksom vilken skola samt vilken lärare som berörts av undersökningen. Enligt Trost (2007) finns det dessutom ”känsliga” personuppgifter som inte får finnas i några som helst dokument. Sådana uppgifter kan till exempel vara ras eller etniskt ursprung, politiska, religiösa eller filosofiska åsikter, eller uppgifter om hälsa, drog och sexualvanor. Denna typ av information tar vi helt avstånd från i vår enkät. Informationen som ges av den första delen av enkäten, d.v.s. fram t.o.m. fråga fyra, är betydande för att ge underlag för att besvara våra frågeställningar. Bakgrundsfrågorna är följaktligen relevanta för vår undersökning. I den andra delen av enkäten söker vi svar på om eleverna har förståelse för och kan använda några av de generella metoder som krävs för beräkning av de olika begreppen area och omkrets för några olika geometriska figurer. Talen som eleverna använder i beräkningarna är tillrättalagda för att göra enkäten smidig att genomföra. Har eleverna tillräcklig förståelse om begreppen kan de också enkelt hitta den rätta lösningen på respektive fråga. Vår avsikt med undersökningen är som bekant förståelse i begreppen area och omkrets men inte undersökning angående räkning t.ex. användning av algoritmer. Därav de förhållandevis enkla tal vi använt oss av i enkätfrågorna. I den tredje och fjärde delen av enkäten är enkätfrågorna utformade med ett kontextuellt sammanhang och i påståendeform. Eleverna tar här ställning till vilket begrepp påståendena handlar om. I denna del av enkäten söker vi information om eleverna har förståelse för begreppen samt om de kan applicera begreppen i verkliga situationer. Vi styrker enkätfrågornas relevans med kursplanen för matematik i grundskolan (Skolverket, 2000). Där finns bland annat följande mål att sträva mot: Skolan skall i sin undervisning i matematik sträva efter att eleven – utvecklar intresse för matematik samt tilltro till det egna tänkandet och den egna förmågan att lära sig matematik och att använda matematik i olika situationer. 20 2.4 Procedur 2.4.1 Pilotstudie Efter att vi utformat vår enkät lät vi fyra elever i samma skolår som vår urvalsgrupp, fylla i frågorna i vår enkät. Eleverna i pilotstudien bestod av en flicka och en pojke från respektive skolår. De har gått i svensk skola under hela sin skolgång. Pilotstudien utfördes på en skola i Skåne, dock inte på någon av de två skolor som ingick i undersökningen. Elevsammansättningen liknar mest fördelningen på kranskommunskolan. Under pilotstudien var vi särskilt lyhörda för eventuella svårigheter som gällde utformningen och språket. Det framkom inga frågor huruvida enkäten skulle besvaras. De frågor som ställdes var av matematisk karaktär, vilket vi inte svarade på eftersom detta kunde varit vägledande för eleverna. Testgruppen fyllde i enkäten på mellan 5 och 8 minuter. Vi drog då slutsatsen att enkäten skulle ta som längst 10-12 minuter att fylla i för eleverna i vår urvalsgrupp. 2.4.2 Praktiskt genomförande av enkätundersökningen För att minska risken för bortfall, vilket vi hela tiden strävade efter, gjorde vi datainsamlingen i så hög grad som möjligt oberoende av andra personer. Vi hade för avsikt att vara med under hela förloppet det vill säga utdelning av enkät - ifyllning av enkät – insamling av enkät. Vi ansåg att det fanns vinster med att följa enkäterna hela vägen eftersom de var väldigt viktiga för vår undersökning. Ett annat förfarande kunde varit att vi ålagt respektive klasslärare att leda själva enkätifyllningen. Detta sätt bedömde vi emellertid som en risk för vår undersökning och därmed för hela vårt examensarbete. Vi tog kontakt med de berörda lärarna på respektive skola för att få godkännande om att uppta deras tid och boka in lämplig tidpunkt för genomförandet av datainsamlingen. Det informationsbrev, se bilaga 2, som varje enkät bör föregås av (Johansson & Svedner, 2006) delades ut av respektive klasslärare cirka en vecka innan vi kom med enkäten till skolorna. Genom detta förfarande gav vi föräldrarna tillfälle att dels kunna ställa frågor om enkäten men också utesluta sitt barn från undersökningen. Vi presenterade vår enkät inför varje klass som skulle fylla i enkäten. Syftet med 21 undersökningen och hur det skulle gå till att besvara enkäten var vi noga med att samtliga elever fick tydlig information om. I presentationen var vi också tydliga med att informera eleverna om att de uppgifter de lämnade var anonyma och frivilliga, men att vi gärna såg att alla svarade så gott de kunde. På överenskommen tid delades enkäterna ut och fylldes i, med ett undantag. En av de åtta klasserna kunde inte medverka vid det överenskomna tillfället så dessa uteblev från undersökningen till en början. Klassläraren lovade emellertid att ordna en ny tid med klassen som vi kunde förfoga över. För att få vår undersökning så komplett som möjligt, med avseende på bortfall, var vi tacksamma för erbjudandet från klassläraren. Efter diverse omständigheter fick vi in 78 respektive 74 enkäter från de båda skolorna. Vi hade då alltså delat ut och samlat in 152 enkäter för bearbetning. 3 Resultat I denna resultatdel kommer vi att visa de resultat som är viktiga för att kunna ge stöd åt att besvara våra frågeställningar. Resultatet redovisas med utgångspunkt från våra frågeställningar vilka även används som underrubriker. Värdena för bortfall som redovisas i detta kapitel är beräknat till de elever, av totalt 152, som svarade ofullständigt på enkäten. 3.1 Förtydligande av kodning på insamlade enkätsvar Då vi utformade enkäten missade vi att koda de olika svarsalternativen. I vår resultatanalys, i såväl text, tabeller och diagram, benämner vi respektive frågas svarsalternativ från vänster till höger med beteckningarna A, B, C, D för frågorna 2-8 som har fyra svarsalternativ. För frågorna 9-16 med vardera två svarsalternativ använder vi beteckningarna A, B. 3.1.1 Val av benämning på kön i enkäten I enkäten valde vi att benämna elevernas kön med tjej eller kille. I efterhand har vi kommit till insikt om att detta kan uppfattas som ett allt för vardagligt språk. Med anledning av detta väljer vi genomgående i detta arbete att istället använda oss av 22 benämningarna flicka respektive pojke eftersom detta är brukligt i litteraturen. 3.2 Finns det brister i förståelse av begreppen area och omkrets, och i så fall vilka? Ur vår enkät söker vi resultat på om eleverna har förståelse för de båda geometriska begreppen area och omkrets för enkla figurer. Frågorna 5-16 i vår enkät, bilaga 1, kan avslöja elevernas eventuella brister i begreppen. Enkätfrågorna är grupperade med avseende på utformning och ger oss en bild av hur väl förståelsen är befäst. Vi har delat upp frågorna enligt följande: Frågorna 5-8 är traditionella beräkningsuppgifter där förståelse krävs om bland annat användandet av geometriska formler. Ur detta ser vi om eleverna behärskar metoderna och använder sig av rätt enheter. Det fanns fyra svarsalternativ. Frågorna 9-11 är frågor med ett kontextuellt innehåll där eleverna presenteras ett sammanhang som handlar om antingen omkrets eller area. Sammanhangen är beskrivna med endast ett fåtal ord för att ej gränsa till test i läsförståelse. Med dessa frågor kan vi möjligen avslöja om de med några få ord förstår och håller isär de olika begreppen. Det fanns två svarsalternativ. Frågorna 12-16 är i påståendeform som besvaras med antingen sant eller falskt. Här testas eleverna om de har förståelsen som krävs för att behärska begreppen i sammanhang som beskrivs med en något längre text än i frågorna 9-11. Det fanns två svarsalternativ. 3.2.1 Resultatanalys av frågorna 5-8 Fråga 5 Här frågades det efter omkretsen av en cirkel med en given diameter om 10cm. På denna fråga svarade dryga 67,1% av eleverna korrekt. Utformningen av det näst frekventa svarsalternativet hade rätt siffror men fel enhet. Detta valde 15,1% av eleverna. Dryga 82 % valde alltså ett alternativ som speglade de rätta siffrorna men några brast i valet av enhet. 2,6 % av eleverna valde alternativet där både siffrorna och enheten var felaktiga. En person hade inte svarat på frågan och är beräknad som att hon/han svarat fel på uppgiften. 23 Fråga 6 I denna fråga skulle eleverna beräkna arean av en cirkel med en given diameter om 20cm. Här angav endast 42,1% av eleverna korrekt svarsalternativ. Nästan lika många, 40,1%, angav det felaktiga alternativet med samma siffror som omkretsens längd, d.v.s. 60, men med en areaenhet. En tiondel av eleverna angav alternativet med både fel siffror och fel enhet. Av enkäten att döma kan endast drygt två femtedelar av samtliga elever i undersökningen, räkna ut och använda rätt enhet för en cirkels area. Fördelningen av de fyra svarsalternativen åskådliggörs i diagram 1. Diagram 1: Diagrammet visar hur stor andel av eleverna som valt de olika alternativen Av de elever som svarade med det korrekta alternativet fanns en signifikant skillnad mellan könen. En tredjedel av flickorna jämfört med hälften av pojkarna svarade rätt på uppgiften. En person hade inte svarat på frågan och är beräknad som att hon/han svarat fel på uppgiften. Fråga 7 Denna fråga var tänkt att ge oss svar på om eleverna behärskade att räkna ut arean för en rektangel med sidorna 10 respektive 25 dm. Som brukligt, var endast en av de två motstående sidorna måttsatta. Glädjande nog var det hela 93,4% som angav det korrekta 24 svarsalternativet, 250dm2. Anmärkningsvärt är också att denna fråga var den som hade näst bäst resultat av alla enkätfrågorna med avseende på frekvensen av korrekta svar. En person svarade inte på frågan och är beräknad som att hon/han svarat fel på uppgiften. Fråga 8 I fråga 8 söker vi omkretsen av en kvadrat med sidan 9dm. Liksom i uppgift 7 är inga överflödiga mått utsatta. För ett korrekt svar på frågan krävdes således förståelse om kvadratens definition, d.v.s. att kvadraten är ett specialfall av rektangeln där alla sidor är lika långa. 62,5% lyckades svara korrekt alternativ på denna uppgift. Det näst vanligaste alternativet, som 17,8% av eleverna svarade, var det som hade korrekt siffror men fel enhet, i detta fall en areaenhet. Två personer hade inte svarat på frågan och är beräknade som att de svarat fel på uppgiften. Sammanfattning av frågorna 5-8 För att sammanfatta resultaten från frågorna 5-8 missar de flesta eleverna på fråga 6. I denna fråga skiljer sig flickornas och pojkarnas svarsfrekvens för det rätta svarsalternativet anmärkningsvärt mycket. Fråga 6 kräver också flest räkneoperationer av de fyra. En förutsättning för att kunna beräkna arean av en cirkel är att man kan och kan använda formeln för detta. Uppgiften krävde alltså att diametern dividerades med 2, till en radie som kvadreras och sedan multipliceras med π, i detta fall avrundat till 3. Dessutom krävdes förståelse om rätt enhet. I övriga tre frågor kan man komma undan med en multiplikation i något av lösningssätten. 3.2.2 Resultatanalys och sammanfattning av frågorna 9-11 Med dessa frågor ville vi med några få ord beskriva en situation som antingen var en area eller en omkretssituation. Inga beräkningar krävdes utan syftet var att undersöka elevernas högst grundläggande förståelse inom begreppen. Svarsalternativen var antingen area eller omkrets och enkätfrågorna löd enligt följande: 9. En lägenhets storlek är 90m2. Uppgiften handlar om… 10. Ölands yta är 1342km2. Uppgiften handlar om… 11. Avståndet runt en sjö. Uppgiften handlar om… Resultatet blev att en stor majoritet svarade korrekt alternativ på respektive fråga. Ordet ”yta” fanns med i fråga 10 vilket en del elever undrade vad det betydde under enkätens 25 genomförande. Diagram 2 förtydligar delresultaten i de olika frågorna. Diagram 2: Svarsfördelning för frågorna 9-11 3.2.3 Resultatanalys och sammanfattning av frågorna 12-16 Frågorna ställdes i påståendeform och alternativen som eleverna kunde välja mellan var antingen ”sant” eller ”falskt”. Resultaten från dessa fem frågor kan delas in i två grupper med betydande skillnader med avseende på frekvensen av korrekt svarsalternativ. På de tre första, 12-14, av de fem frågorna har cirka tre fjärdedelar av eleverna svarat korrekt alternativ. På de två sista frågorna, 15-16, har däremot endast drygt hälften svarat korrekt. Diagram 3 visar fördelningen av den relativa frekvensen för de fem olika frågorna, 12-16. 26 Diagram 3: Svarsfördelning för frågorna 12-16 27 3.3 Vilka resultatmässiga skillnader med avsikt på kön visar undersökningen? Vi väljer att redovisa resultatet, uppdelat efter kön, från de olika typerna av frågor, nämligen frågorna 5-8, 9-11 och 12-16. Det visade sig att vissa resultatmässiga skillnader uppstod i dessa tre olika grupperna av frågor, mellan könen. Till sist gör vi också en jämförelse av den totala medelpoängen för flickor respektive pojkar. 3.3.1 Resultatanalys och sammanfattning av frågorna 5-8 På de fyra frågorna, vilka testade bland annat förståelse om användandet av geometriska formler och räkning, hade flickorna en medelpoäng som uppgick till 2,57 poäng av 4 möjliga. Detta ger en korrekt svarsfrekvens på 64,2% för de fyra frågorna. Av samma frågor hade pojkarna en medelpoäng på 2,73 poäng av 4 möjliga. Svarsfrekvensen för de rätta alternativen blev i pojkarnas fall 68,3%. Om flickorna och pojkarnas resultat för varje fråga jämförs finner vi den största skillnaden i fråga 6. Här har 33,8 % av flickorna svarat rätt på frågan. Bland pojkarna är motsvarande siffra 50,0 %. Detta ger alltså en förhållandevis stor skillnad i lösningsfrekvens mellan könen på just denna fråga. På fråga 7 får flickorna en större andel korrekta svar. Lösningsfrekvensen för det rätta alternativet blev 96 % för flickorna och 91 % för pojkarna. Resultatet av de övriga två frågorna 5 och 8 får pojkarna högst lösningsfrekvens. Det är dock ingen stor skillnad. Totalt hade pojkarna högst lösningsfrekvens på dessa fyra frågorna. En helhetsbild, av frågorna 5-8, med avsikt på kön visas i diagram 4. 28 Diagram 4: Andel som svarat korrekt fördelat på respektive kön. 3.3.2 Resultatanalys och sammanfattning av frågorna 9-11 På frågorna 9-11, som testade om eleverna ur ett sammanhang beskrivet med få ord, fanns det även i dessa frågor en skillnad, om än liten, i resultatet med avsikt på kön. Av flickorna svarade 96,4% korrekt alternativ på de tre frågorna. Pojkarnas motsvarande resultat var 89,3% korrekta svar. Den största skillnaden fanns i fråga 10 där hela 97,3% av flickorna svarade rätt mot 84,6% av pojkarna. Flickorna hade således en något högre lösningsfrekvens på dessa tre frågorna. 3.3.3 Resultatanalys och sammanfattning av frågorna 12-16 På de avslutande fem frågorna, som innehöll påståenden med något fler ord, hade flickorna en något högre andel rätt än pojkarna. Fördelningen blev att flickorna i genomsnitt hade 67,0% rätt på de fem frågorna medan pojkarna i genomsnitt uppnådde 64,4% rätt. Den största skillnaden fanns i fråga 14 där flickorna hade knappa 80 % rätt och pojkarna dryga 69 % rätt i genomsnitt. Som en sammanfattning av resultaten från de tre olika frågeområdena hade pojkarna i genomsnitt bättre resultat på de inledande frågorna där formler och räkning krävdes. 29 Flickorna hade i genomsnitt flest rätt på frågorna 9-16 som var åt det kontextbaserade hållet. 3.3.4 Jämförelse av totalpoäng Om den sammanslagna poängen, det vill säga den totala poängen som eleverna kunde uppnå, jämförs mellan pojkarna och flickorna var flickorna något bättre. De hade i genomsnitt 8,80 poäng vilket är 73,3% rätt på de tolv uppgifterna. Pojkarna uppnådde i genomsnitt 8.62 poäng vilket uttryckt i procent är 71,8%. Den poängmässiga skillnaden är således liten men uppträder dock. Skillnader, om än små, mellan könen uppkom i de tre olika grupperna av frågor. Dessa jämnades dock ut, enligt ovan resultat, sett över hela enkäten. 3.4 På vilket sätt framträder olika resultat beroende av antal år i svensk skola? Vi väljer att dela upp populationen i två grupper med avseende på antal år i svensk skola. I den ena gruppen har vi elever i skolår 8 och 9 som gått i svensk skola mellan 2 och 7 år. Antalet i denna grupp var 19 elever. Den andra gruppen har gått i svensk skola mellan 8 och 9 år och var 133 till antalet. Då vi formulerade denna forskningsfråga trodde vi att fördelningen (19/133) skulle vara något jämnare. Resultatet redovisas för de två grupperna enligt ovan i form av delsummor av poängen för frågorna 5-8, 9-11 och 12-16 samt totalpoäng. 3.4.1 Resultatanalys och sammanfattning av frågorna 5-8 På dessa fyra frågorna hade de 19 eleverna i gruppen 2-7år i svensk skola i genomsnitt 59 % rätt. Motsvarande siffra för eleverna i den andra gruppen, med 133 elever, var 67 % rätt. Eleverna i gruppen med längre svensk skolgång hade alltså en högre genomsnittspoäng. 3.4.2 Resultatanalys och sammanfattning av frågorna 9-11 I denna grupp av frågor blev resultatet likt den föregående gruppen av frågor. Genomsnittet var 84 % uppnådda poäng för eleverna med 2-7 års erfarenhet från svensk 30 skola och 94 % för den andra gruppen vilket visar på att det finns en skillnad. 3.4.3 Resultatanalys och sammanfattning av frågorna 12-16 På de fem frågorna, som var utformade med ett kontextuellt sammanhang, skiljde sig inte resultatet något nämnvärt i förhållande till de övriga frågorna. De genomsnittliga poängen i de två grupperna var 57 % bland eleverna i gruppen med kortast tid i svensk skola, jämfört med 67 % i den andra gruppen. 3.4.4 Jämförelse av totalpoäng Ur ovan nämnda siffror finner vi att gruppen med kortast erfarenhet av svensk skola uppnådde i genomsnitt 64 % av maxpoängen. Detta att jämföra med 74 % för den andra gruppen. Sammanfattningsvis finner vi, av resultatet att döma, att eleverna med den kortare erfarenheten av svensk skola får en något lägre genomsnittspoäng på enkäten. Skillnaden grupperna emellan är förhållandevis jämn sett över de tre grupperna av frågor. Skillnaderna var i princip samma för grupperna av frågor 5-8 och 12-16. Dessa grupper av frågor skiljer sig som bekant med avseende på utformning. 31 4 Diskussion 4.1 Resultatets tillförlitlighet Vår bestämda uppfattning om den undersökning vi genomfört är att det inte går att göra några generaliseringar för alla Sveriges elever i skolår 8 och 9. Detta har inte heller varit syftet med vår enkätundersökning utan snarare har målet varit att visa på om vår uppfattning och tidigare studier, som pekat på bristande förståelse för begreppen area och omkrets även gäller för de skolor som deltagit i vår undersökning. När det gäller enkäten som ligger till grund för hela arbetet, var vi väldigt noga med att den skulle vara konkret och välformulerad så att uppgifter och påståenden som kunde missförstås av informanterna skulle vara klart begränsad. Vi var också väldigt konsekventa med tillvägagångssättet för att genomföra enkätundersökningen på totalt 8 klasser fördelade på 2 skolor i södra Sverige. Vi åkte till vardera en skola där vi var med under hela processen från utlämning, genomförande och insamling. Detta innebar att samtliga utlämnade enkäter - 152 stycken - besvarades och returnerades och bortfallet med ofullständiga svar var ytterst begränsat. Informantgruppen var tämligen balanserad med avseende på kön i det att den bestod av 74 flickor och 78 pojkar. I undersökningen där vi valt att dela upp enkäten i olika delar med avsikt att få olika infallsvinklar till begreppen har vi förutom fråga 1 som handlar om hur många år eleven gått i svensk skola delat in det enligt följande: Fråga nr 2-4 handlar om attityd till och nytta med skolmatematiken Fråga nr 5-8 är geometriuppgifter som liknar rena räkneuppgifter Fråga nr 9-11 är påståenden där eleven ska välja mellan area eller omkrets Fråga nr 12-16 behandlar påståenden där valet står mellan sant eller falskt Värdena vi får av antalet rätt svar som informanterna fått handlar om frågorna med nummer 5-16 som totalt kan ge 12 rätt. Detta är frågor med fasta svarsalternativ där endast ett svar är korrekt. På frågorna 5-8 är svarsalternativen fyra till antalet medan resterande frågor 9-16 endast innehåller två alternativ per fråga. Det finns alltid en risk att några elever tolkar frågorna felaktigt och därför var vi noga 32 med att innan enkäten delades ut, förklara vad enkäten handlade om, trolig tidsåtgång, anonymitet och att enkäten bestod av fasta svarsalternativ att välja mellan förutom på fråga 1. Det insamlade datamaterialet har vi bearbetat i huvudsak med hjälp av Excel. Ett annat verktyg vid bearbetning av datamängder är SPSS. Eftersom vi endast har kunskap om det förstnämnda verktyget och att de värden vi var ute efter gick att få fram med detta verktyg valde vi Excel. I samråd med vår handledare anser vi att denna bearbetning är tillräcklig för vår undersökning. Även om en undersökning med enbart enkät som underlag kan påvisa brister såsom ytliga svar och svårighet i att tolka ärligheten hos de svarande, är vår bedömning utifrån det sätt vi genomfört hela processen att reliabilitet och validitet är tämligen stor. Vi är medvetna om att graden av förståelse hos varje enskild elev inte fullt ut kan mätas i denna undersökning. Mänskliga faktorer spelar naturligtvis en viss roll i sammanhanget. Dessa kan exempelvis vara slarvfel, grupptryck eller ouppmärksamhet. I följande avsnitt kommer vi att redovisa resultatet med utgångspunkt och fokus i våra frågeställningar relaterat till vad vi funnit i litteraturen. 4.2 Finns det brister i elevers förståelse av begreppen area och omkrets, och i så fall vilka? Eftersom vi i skolans värld har till uppgift att följa läroplan (Skolverket, 1994) och kursplan (Skolverket, 2000) är det av största vikt att studier och forskning fortlöpande sker på alla nivåer huruvida måluppfyllelse sker eller ej. När det gäller geometri i stort och förmågan att kunna skilja på area och omkrets i synnerhet står det bland annat i dessa verktyg att kunskap inte bara handlar om fakta utan framförallt om förståelse och att kunna tillämpa det i vardagslivet. Att kunna ha en rumsuppfattning och förmågan att kunna mäta längder och areor är viktiga delar i matematiken som på olika sätt kan hjälpa till i vardagslivet. Anderberg (1992) som vi har använt oss av en hel del i lärarutbildningen poängterar att det inte räcker med att lära sig regeln att arean beräknas med längden multiplicerat med bredden för detta leder bland annat till svårigheter med att skilja de båda begreppen åt. Skillnaden mellan inlärning av regler istället för en kunskap som består av att veta hur något beräknas i kombination med varför det beräknas på det aktuella sättet beskriver 33 Skemp (1976) i en intressant studie där han skiljer på relationell och instrumentell förståelse. Vår egen uppfattning i kombination med mycket av de studier vi tittat på sker den mesta undervisningen och kunskapsinlärning på instrumentell nivå. Det är fortfarande matematikboken som regerar och styr elevers kontakt med matematiken i skolan med alltför mycket av tyst enskild räkning. Av den litteratur vi tagit del av som sträcker sig över ett sekel är uppfattningen ofta densamma att läraren fyller en viktig funktion genom att sträva efter att förändra matematikundervisningen från ett abstrakt ämne till ett mera konkret arbetssätt. Kruse (1909) konstaterade att matematiken måste konkretiseras för en ökad förståelse bland elever. Detta konstaterar även Nilsson (2005) i sin avhandling från 2005 där han betonar ökad förståelse genom ett aktivt laborativt räknande bland elever. Dock betonar han att laborativt lärande inte per automatik innebär ökad förståelse utan det ställer stora krav på lärarens kunskap och engagemang i läroprocessen. Vår uppfattning av resultatet i vår undersökning visar på att ett flertal elever har brister i att skilja på area och omkrets. Kommentarer från elever i samband med enkäten som också förstärker vår uppfattning är: ”- Vad är geometri?” ”- Vad är yta?” ”- Det var ju längesen vi hade detta?” - syftar på geometri. Det som är mest uppseendeväckande är när vi jämför det totala medelvärdet för eleverna i skolår 8 med det totala medelvärdet i skolår 9 på de båda skolorna. Eleverna i skolår 8 uppnår ett bättre resultat än sina kamrater i skolår 9. Emellertid inte så mycket på storstadsskolan som för kranskommunskolan men bara det att åttorna har bättre resultat än sina äldre kompisar är anmärkningsvärt. Medelvärde Kranskommun Storstad Skolår 8 9,74 8,05 Skolår 9 9,19 7,86 34 Orsakerna till denna skillnad kan vi bara spekulera i men följande faktorer kan ha påverkan. En av orsakerna kan vara att eleverna i skolår 8 studerat det tvådimensionella området i nära anslutning till undersökningen medan eleverna i skolår 9 studerat det tredimensionella området i geometri. En annan orsak kan vara att förståelsen verkligen är högre bland eleverna i skolår 8. När vi studerar avsnittet med geometriuppgifter, fråga 5-8, visar det sig att fråga 7 som behandlar arean av en rektangel gav mest korrekta svar 93,4% . Fråga 5 samt 8 som båda handlar om omkrets dels av en cirkel på fråga 5 och en kvadrat på fråga 8 har en träff på antalet rätt med 67,1% samt 62,5%. Den svåraste frågan torde vara fråga 6 som tar upp en cirkels area som endast 42,1% av samtliga elever har svarat korrekt på. När det handlar om det höga resultatet på fråga 7 tar vi på oss lite självkritik eftersom vi i denna fråga inte var konsekventa jämfört med övriga. I de tre övriga frågorna hade vi svarsalternativen parvis med angivande av siffror men olika enheter men av någon anledning gjorde vi inte så i fråga 7 där vi hade ett parvis resultat medan övriga två hade samma enhet men olika siffror. Vi antar att detta har spelat roll såtillvida att informanterna snabbt valt bort de alternativ som var parvis och det som återstod då var två alternativ där egentligen bara ett känns riktigt rimligt vilket medfört att uteslutningsförmågan lett fram till det korrekta alternativet - därav den höga procentsatsen 93,4%. Bortfall på grund av ofullständigt ifyllda enkäter var i detta avsnitt 1 för fråga 5-7 samt 2 när det gäller fråga 8. I nästa avsnitt fråga 9-11 där det gällde att ta ställning till om ett textpåstående handlade om omkrets eller area var antalet korrekta svar totalt sett det högsta på hela enkäten. Antalet korrekta svar var i fråga 9 - 92,8%, fråga 10 - 90,8% och fråga 11 - 94,7%. Det avslutande avsnittet fråga 12-16 var också påstående av lite mer text där alternativen stod mellan sant eller falskt. Här sjönk de korrekta svaren generellt men framförallt på de två sista påståendena där den korrekta svarsfrekvensen låg på cirka hälften av inlämnade svar. Antalet korrekta svar i fråga 12-16 var 12 - 74,3%, 13 - 76,3%, 14 - 74,3%, 15 - 52,6% samt 16 - 50,7%. 35 I likhet med de studier och den litteratur vi tagit del av får vi konstatera att brister i att skilja mellan begreppen area och omkrets finns. Det som har visat sig vara störst problem för våra informanter är vad gäller geometriuppgifterna fråga 5-8 när de fyra svarsalternativen är parvis lika vilket leder till att om man inte är helt säker men utesluter två alternativ finns fortfarande två alternativ kvar att välja på. Detta kunde eleverna kringgå i uppgift 7 vilket vi på ett sätt beklagar men på ett annat sätt gör att detta konstaterande blir tydligare. I textavsnitten blev det blandat resultat där vår slutsats bygger på att i frågorna 9-11 är det väldigt korta påståenden vilket gör det tydligare för eleven att ta ställning. I avsnittet med frågorna 12-16 ökar textmängden och därmed svårighetsgraden vilket också visar sig på antalet korrekta svar. Påpekas bör att fråga 9-16 endast har två svarsalternativ vilket gör att sannolikheten för att gissa rätt är 50%. Vi anser att enkäten i sin helhet ger en bild av elevernas förståelse för begreppen. Varje enskild fråga ger en indikation av förståelse för det som efterfrågas. Efter samråd med vår handledare blev vår slutsats att våra enkätfrågor skulle ligga till grund för att ge oss svar på våra frågeställningar. Detta beskrivs ovan under kapitel 2.3 Val av enkätfrågor. 4.3 Vilka resultatmässiga skillnader med avsikt på kön visar undersökningen? Evenshaug & Hallen (2001) beskriver studier som handlar om könsskillnader där flickor generellt är bättre än pojkar när det handlar om språket medan pojkar i traditionella intelligenstester som handlar om matematiskt tänkande och visuell och spatial förmåga har ett bättre resultat. Vår undersökning, där fördelningen mellan könen var 74 flickor och 78 pojkar, i likhet med dessa studier vittnar om att det finns skillnader även om de är förhållandevis små. När vi studerar enkätens resultat med avseende på kön kan vi konstatera att snittet för flickorna slutade på 8,8 rätt eller 73,3% av det totala antalet rätt som var 12. Motsvarande resultat för pojkarna var 8,6 rätt eller 71,8 % av det totala. Tittar vi vidare på resultaten i de olika avsnitten blir det i fråga 5-8 rätt svarsfrekvens med 64,2 % för 36 flickorna och 68,3% för pojkarna. I nästa del fördelades antalet rätt med 96,4% för flickorna och 89,3% för pojkarna. I det sista avsnittet med fråga 12-16 fick vi 67,0% korrekta svar av flickorna och 64,4% rätt av pojkarna. Vår slutsats utifrån detta material är att tidigare studier som är stabila över tid även tycks gälla för denna lilla undersökning där flickorna totalt sett presterar något bättre men där pojkarna har ett övertag på rent matematiska uppgifter och flickorna är bättre på de språkliga delarna. 4.4 På vilket sätt framträder olika resultat beroende av antal år i svensk skola? När det gäller informanterna i vår undersökning är de uppdelade på två skolor där det finns väsentliga skillnader vad gäller exempelvis invandrartäthet. Elever med annat modersmål än svenska är väldigt ovanligt i kranskommunskolan medan skolan i storstaden till stor del består av elever med annat modersmål än svenska. Fördelningen av elever mellan de båda skolorna är 78 från skolan i kranskommunen och 74 från skolan i storstaden. Av en händelse är fördelningen mellan skolorna samma fördelning som gäller mellan könen men detta är inget annat än en ren tillfällighet och det är alltså inte på det viset att den ena skolan är för endast pojkar och tvärtom. I planeringen av undersökningen drog vi därmed slutsatsen att eftersom det är dessa stora skillnader mellan skolorna vad gäller modersmålet kan det vara av intresse att undersöka om detta kan vara en faktor som påverkar resultatet. Engström (1998) menar att språket har en viktig roll i varje individs lärande totalt sett och när det gäller matematik i synnerhet, framförallt om det är uppgifter med mycket text. Dock när det gäller avsnittet om geometri kan det vara av något mindre betydelse då det i många sammanhang handlar om spatial förmåga. Det enda som eventuellt ger oss delvis information om etnicitet förutom vad vi själva konstaterat när vi varit på plats är fråga 1 där informanten ska ange hur många år han/hon gått i svensk skola. Såsom vi förutsåg besvarades denna fråga på skolan i kranskommunen med antingen 8 eller 9 år förutom en flicka som gått 4 år i svensk skola. På skolan i storstaden var det mer blandat med allt från 2 år till 8-9 år. Utifrån dessa faktorer i kombination med vår egen erfarenhet från skolorna är vår slutsats att språket spelar roll i likhet med den litteratur vi hänvisar till. Rent faktamässigt fördelade sig antalet år i svensk skola på alla informanter enligt följande: 37 Antal år 2 3 4 5 6 7 8 9 Antal informanter 5 3 2 3 2 4 65 68 När vi tittar på resultatet i detta avseende gör vi jämförelser mellan de båda skolorna eftersom vi anser att det finns skillnader i elevers modersmål även om det inte klart framkommer av vår fråga där totalt 133 av 152 elever eller 87,5% har gått i svensk skola under hela sin skoltid. När det gäller för den invandrartäta skolan i storstaden uppgick medelvärdet för antal rätt till 7,9 rätt av totalt 12 eller 65,8% korrekta svar. Motsvarande siffror för skolan i kranskommunen blev 9,5 rätt av 12 eller 79,2%. Det är vår uppfattning att det är en klar skillnad på resultaten men huruvida det beror på språket enbart eller en kombination av orsaker vill vi låta vara osagt. För att studera några skillnader i antalet korrekta svar tittar vi lite djupare på geometriuppgifterna som är fråga nr 5-8: Fråga nr 5 6 7 8 Procentuellt rätt svar för Storstad 62% 41% 90% 50% Kranskommun 73% 44% 97% 76% Genomgående har eleverna i kranskommunen bättre svarsfrekvens än eleverna i storstaden. Svarsalternativen till geometriuppgifterna har olika enheter beroende på om det handlar om omkrets eller area men i övrigt är det rent matematiskt kunnande som gäller, förutom frågan med kortare text. Vår uppfattning är att språket spelar in men utifrån Engströms (1998) studier där han menar att geometrisk problemlösning förutsätter ickespråkliga kunskaper torde innebära att det är andra faktorer som också är av betydelse. 38 4.5 Slutsatser Eftersom vi under vår verksamhetsförlagda tid under lärarutbildningen kommit i kontakt med ett antal elever som uppvisat problem med geometri i huvudsak och att skilja på begreppen area och omkrets i synnerhet var valet ganska enkelt för vad vi ville vår undersökning skulle inrikta sig på. Dessutom har den litteratur vi tagit del av, i stor utsträckning påvisat att elever i grundskolan haft problem med detta område, under lång tid. Med vår begränsade, men i vårt tycke genomtänkta enkätundersökning vill vi försöka få ytterligare underlag för om dessa brister även gäller för de skolor vi undersökt. I fortsättningen av detta avsnitt sammanfattas de slutsatser vi tycker oss kunna dra av undersökningen relaterad till respektive frågeställning. Utifrån det resultat vi redovisat ovan när det gäller antalet rätt svar på enkäten är vår bestämda uppfattning att de undersökta skolorna också uppvisar brister i begreppen area och omkrets. Det är givetvis svårt att precisera hur många rätt eleverna bör ha på enkäten för att kunna påstå att det inte finns brister, men oavsett detta faktum är det ej godtagbart att exempelvis eleverna i skolår 8 har bättre genomsnitt än sina kamrater i skolår 9. Den totala poängen är beräknad att varje fråga ger en poäng. Detta kan bli missvisande med anledning av att fyra frågor har fyra svarsalternativ och övriga åtta frågor bara två svarsalternativ. Genom att bara ta hänsyn till totalpoängen är det svårt att dra slutsatser om elevernas verkliga förståelse om begreppen. För att öka validiteten av vår undersökning borde vi haft en annan poängfördelning av enkätfrågorna. Frågorna 5-8 ger eleven mindre chans att, utan förståelse, gissa rätt men ger samma poäng som de övriga frågorna i enkäten. Både litteraturen och vår egen erfarenhet visar på att många elever lär sig i bästa fall regler för hur något ska räknas ut. Huvudsyftet är att ta sig igenom kommande prov men eleverna saknar många gånger den korrekta förståelsen för vad det är som ska uträknas. Detta leder i förlängningen till att förståelsen inte består någon längre tid och gör att i en undersökning med en inte alltför hög svårighetsgrad som består av fasta svarsalternativ innehåller ett större moment av gissning. I geometriuppgifterna nr 5-8 finns 4 svarsalternativ vilket innebär 25 % chans att gissa rätt medan övriga 8 frågor, nr 9-16, endast innehåller 2 svarsalternativ med en sannolikhet att träffa rätt vid gissning på 50 39 %. När vi då har svar på frågorna som uppvisar en korrekthet på 40-50 %, fråga 6 och 8, visar detta klart på brister. För övrigt handlar fråga 6 om area och fråga 8 behandlar omkrets så bristerna gäller över hela linjen. Fortsätter vi att titta på antalet rätt på enkäten ser vi relativt små skillnader beroende av om det är en flicka eller pojke som svarat. När det gäller snittet för flickorna hamnar det på 8,8 rätt eller 73,3% medan pojkarnas resultat blir 8,6 eller 71,8% korrekta svar. Däremot är det intressant att konstatera, när vi tittar per avsnitt av enkäten, de likheter med tidigare forskning som framskymtar även i vår undersökning. Rent matematiskt tänk som det handlar om i uppgift 5-8 ger rätt svarsfrekvens med 64,2% för flickorna och 68,3% för pojkarna vilket stämmer överens med litteraturen att pojkar generellt har något bättre resultat i matematiskt tänkande och spatial förmåga. I den delen som handlar om text i form av mindre påståenden, fråga 9-11, blir resultatet att antalet rätt var 96,4% för flickorna och 89,3% för pojkarna. Däremot i sista delen, något mer och svårare text, frågorna 12-16 sjunker det totala antalet rätt till 67,0% korrekta svar av flickorna och 64,4% rätt av pojkarna. Det vi kan konstatera är att detta också stämmer med tidigare forskning som säger att flickor generellt är bättre än pojkar när det handlar om språket. Vår uppfattning om de båda skolorna, var att svaren skulle visa på skillnader beroende på att kranskommunskolan i stort sett bara har svenskfödda elever medan skolan i storstaden har stor andel invandrarbarn. Dock visade det sig i svaren på fråga ett att totalt 133 av de 152 eleverna gått 8 alternativt 9 år i svensk skola. Detta speglar på intet sätt skillnaderna i etnicitet på de båda skolorna. Däremot är vi på det klara med att språket är en viktig faktor i förståelsen av begreppen area och omkrets. Eftersom det är en stor andel elever i storstaden som har annat modersmål än svenska och det är tvärtom med eleverna i kranskommunen drar vi slutsatsen att det generellt bättre resultatet hos eleverna i kranskommunen till stor del kan bero på språket. För att ta ett resultat för de båda skolorna som visar skillnaden i resultat var snittet för eleverna i storstadsskolan 7,9 rätt av totalt 12 eller 65,8% korrekta svar. Motsvarande siffror för skolan i kranskommunen blev 9,5 rätt av 12 eller 79,2%. Det är vår uppfattning att enbart lägga skulden på språket är att dra något förhastade slutsatser men att det har stor inverkan bekräftar den litteratur vi angett tidigare i detta arbete. 40 4.5.1 Egna tankar och reflektioner Under vår lärarutbildning har vi i flertalet kurser kommit i kontakt med en mängd olika laborativa undervisningsmoment. Detta gäller framförallt inom området geometri. Vår uppfattning är att dessa tillfällen har medfört en ökad kunskap och förståelse av de olika geometriska begreppen för oss som studenter. Vi tror att detta undervisningssätt också är användbart på grundskoleelever för en djupare förståelse. Uppmärksamhet bör dock tillägnas på vilket sätt laborationer leds och sätts in i sitt pedagogiska sammanhang. 4.5.2 Förslag till vidare forskningsfrågor Vad kan elevernas bristande kunskap om begreppen area och omkrets bero på? Är laborativ matematikundervisning enda lösningen för bättre kunskap och förståelse i geometri? 41 Referenslista Litteraturreferenser Aasa Elisabeth (red.) (2004) Matematik - ett kärnämne. Nämnaren Tema. Göteborg: Nämnaren Göteborgs universitet Ahlström Ronny (red.) (2005). Matematik - ett kommunikationsämne. Nämnaren Tema. Göteborg: Nämnaren Göteborgs Universitet Anderberg, Bengt (1992). Matematikmetodik i grundskolan. Stockholm: Bengt Anderberg Läromedel Brandell, L. (1999). Räcker kunskaperna i matematik? Högskoleverket Carlsson, Synnöve, Hake, Karl-Bertil och Öberg, Birgitta. (2002). Matte Direkt år 8. Stockholm: Bonnier Utbildning AB Carlsson, Synnöve, Hake, Karl-Bertil och Öberg, Birgitta. (2003). Matte Direkt år 9. Stockholm: Bonnier Utbildning AB Emanuelsson, Göran & Johansson, Bengt & Ryding, Ronnie (red.). (1991). Problemlösning. Lund: Studentlitteratur Engström, Arne (1998). Matematik och reflektion. Lund. Studentlitteratur Evenshaug, Oddbjörn & Hallen, Dag (2001). Barn- och ungdomspsykologi. Lund: Studentlitteratur Gärdenfors. P. (1997). Innan talet fanns. Om språkets evolution. I: H. Andersson & E. Österberg (Red.) Tystnader. Lund: Studentlitteratur. S. 7-15. 42 Hedrén, R. (1992).Van Heile-nivåer och deras betydelse för geometriundervisningen. I G.Emanuelsson, B. Johansson & R. Ryding (red.), Geometri och statistik. Lund: Studentlitteratur Humanistisk – samhällsvetenskapliga forskningsrådet (1996). Etik. Forskningsetiska principer för humaniora och samhällsvetenskap. Stockholm: HSFR. Johansson, B., & Svedner, P.O. (2006). Examensarbetet i lärarutbildningen. Undersökningsmetoder och språklig utformning. Uppsala: Kunskapsföretaget Kilborn, Wiggo (1992). Didaktisk ämnesteori i Matematik- del 3 - Mätning, Geometri, Funktioner, Sannolikhetslära och statistik. Malmö: Almqvist & Wiksell Förlag AB Kilpatrick, J., Swafford, J & Findell, B. (2001). Adding it up. Helping Children learn Mathematics. Washington, DC: National Academy Press. Kruse, A. (1909). Åskådningsmatematik. Stockholm: P.A. Nordstedt & Söners Förlag Littler, Graham & Jirotkova, Drina (2007). Att lära om geometriska kroppar. NCM Göteborg: Göteborgs universitet Lundkvist, Maria & Svensson, Sandra (2005). Elevers förståelse för det matematiska begreppet area. Lärarexamensuppsats. Malmö: Malmö Högskola, NMS Löthman, A. (1992). Om matematikundervisning – innehåll, innebörd och tillämpning. Uppsala: Acta Univesitatis Upsalarnsis Nilsson, Gunnar (2005). Att äga Praxisnära studier av lärarstudenters arbete med geometrilektioner. Avhandling Diss. Göteborg: Göteborgs Universitet Patel, R., & Davidsson, B. (2003) Forskningsmetodikens grunder. Att planera, genomföra och rapportera en undersökning. Lund: Studentlitteratur 43 Piaget, J. & García, R. (1989) Psychogenesis and the history of science. New York: Colombia University Press Sfard, Anna (1991). On the dual nature of Mathematics Concepcions: reflektions on processes and objekts as different sides of the same coin. Educational Studies in Mathematics, 22(1), 1-36 Skemp, Richard R. (1976). Relational and Instrumental Understanding. Mathematics Teaching, Bulletin of the Association of Teachers of Mathematics, 77, 20-26. Skolverket (2000). Grundskolans kursplaner och betygskriterier. Stockholm: Skolverket Undvall, Lennart & Olofsson, Karl-Gerhard & Forsberg, Svante (1997). Matematikboken Y grön för grundskolans senare del. Stockholm: Liber AB Utbildningsdepartementet (1994). Läroplan för det obligatoriska skolväsendet, förskoleklassen och fritidshemmet. Stockholm: Utbildningsdepartementet. Trost, Jan (2007). Enkätboken. Uppsala: Studentlitteratur Wigforss, Frits (1952). Den grundläggande matematikundervisningen. Stockholm: Bergvalls Förlag 44 Webbreferenser Nationalencyklopedin (2008a). Nationalencyklopedins Internettjänst. Hämtades 200812-12 från http://www.ne.se.support.mah.se/artikel/117351 Nationalencyklopedin (2008b). Nationalencyklopedins Internettjänst. Hämtades 200812-12 från http://www.ne.se.support.mah.se/artikel/1545826 Nationalencyklopedin (2008c). Nationalencyklopedins Internettjänst. Hämtades 200812-12 från http://www.ne.se.support.mah.se/artikel/178646 45 Bilagor Bilaga 1 Enkät till elever Enkäten är anonym vilket innebär att du inte behöver ange ditt namn. Ålder:___ Tjej □ Klass:___ Kille □ 1. Hur många år har Du gått i svensk skola? ______ 2. Vad tycker Du om matematik? Tråkigt □ Ganska tråkigt □ Ganska roligt □ Roligt □ 3. Vad tycker Du om geometri? Tråkigt □ Ganska tråkigt □ Ganska roligt □ Roligt □ 4. Har Du nytta av matematiken som Du lär dig i skolan? Lite □ Ganska lite □ Ganska mycket □ Mycket □ Besvara följande geometriuppgifter genom att välja det alternativ du tycker är mest rimligt. 5. Ungefär hur stor omkrets har cirkeln? 10cm 15cm □ 30cm □ 15cm2 □ 46 30cm2 □ 6. Ungefär hur stor area har cirkeln? 20cm 60cm □ 300cm □ 60cm2 □ 300cm2 □ 70m2 □ 250m2 □ 81dm □ 81dm2 □ 10m 7. Hur stor är rektangelns area? 25m 70m □ 35m2 □ 8. Hur stor är kvadratens omkrets? 9dm 36dm □ 36dm2 □ 47 Ta ställning till följande påståenden genom att kryssa i ett av alternativen. 9. En lägenhets storlek är 90m2. Uppgiften handlar om… 10.Ölands yta är 1342km2. Omkrets □ Area □ Uppgiften handlar om… 11.Avståndet runt en sjö. Omkrets □ Area □ Uppgiften handlar om… Omkrets □ Area □ Välj alternativ – Sant eller Falskt 12.När man räknar ut omkretsen vill man veta hur stor yta en figur har! Sant □ Jag tycker påståendet är… Falskt □ 13.En kvadrat med sidan 3cm har arean 9cm2! Sant □ Jag tycker påståendet är… Falskt □ 14.Om man fördubblar både längden och bredden i en rektangel blir omkretsen dubbelt så stor! Sant □ Jag tycker påståendet är… Falskt □ 15.Du räknar ut triangelns area genom att multiplicera basen med höjden! Sant □ Jag tycker påståendet är… Falskt □ 16.Om en halvcirkel och en cirkel har samma diameter, har halvcirkeln hälften så lång omkrets som den hela cirkeln! Sant □ Jag tycker påståendet är… Tack för din medverkan! 48 Falskt □ Bilaga 2 - Föräldrainformation Malmö 2008-11-15 Hej föräldrar Vi är två blivande lärare med matematik som huvudämne och med inriktning mot grundskolans senare år. Vår utbildning har vi erhållit vid Lärarutbildningen på Malmö Högskola där vi just nu håller på med det avslutande examensarbetet. Vårt arbete syftar till att undersöka om elever i grundskolan, år 8 och 9, kan skilja på de geometriska begreppen area och omkrets. Undersökningen består av en enkät med totalt 16 frågor som behandlar detta ämne och där vi har angett fasta svarsalternativ att ta ställning till. All information kommer att behandlas anonymt. Det är vår lagstadgade skyldighet att informera er för att få genomföra en studie av detta slag. Om ni har några invändningar mot vår undersökning eller några andra funderingar kring vår studie så är ni välkomna att kontakta oss: Peter Garmfors, lärarkandidat Kenth Johnsson, lärarkandidat Mobil: 0704-07 01 01 Mobil: 0733-96 77 65 Vänliga hälsningar Peter & Kenth 49