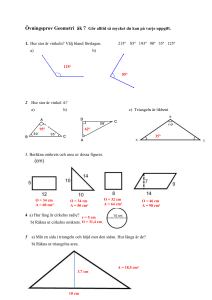
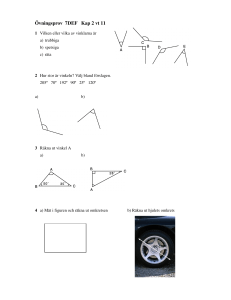
Elevers förståelse för begreppen area och omkrets

School of Mathematics and Systems Engineering
Reports from MSI - Rapporter från MSI
Elevers förståelse för begreppen area
och omkrets
Malin Eriksson
Gustav Olsson
Feb
2008
MSI
Växjö University
SE-351 95 VÄXJÖ
Report 08014
ISSN 1650-2647
ISRN VXU/MSI/MDI/E/--08014/--SE
Examensarbete 15 högskolepoäng
i Lärarutbildningen
Höstterminen 2007
ABSTRAKT
Malin Eriksson och Gustav Olsson
Elevers förståelse för begreppen area och omkrets
Students comprehension about the concepts area and circumference
Antal sidor: 34
Syftet med detta examensarbete är att undersöka om och hur elever uppfattar begreppen omkrets
och area. Då vi båda studerar till matematiklärare anser vi att detta arbete kan stärka oss i vår
lärarroll samt utveckla oss inom arbetsområdet geometri.
Vi började med att göra en diagnos med ca 40 elever. Genom att djupintervjua tre av eleverna
fick vi en bättre förståelse för varför eleverna svarade som de gjorde på diagnosen.
Genom att göra en läromedelsgranskning av de aktuella läroböckerna ville vi se om dessa kan
spela roll när det gäller elevernas kunskap inom detta område.
Resultatet visar att de flesta eleverna klarade att räkna uppgifter inom området omkrets eller
area och använda sig av dessa begrepp när uppgiften var ”given”, på så sätt att eleverna får veta
vad som ska räknas ut (area eller omkrets). Problemen dyker upp när eleverna får svårare
uppgifter som är konstruerade på ett sådant sätt att de inte får en given metod att lösa uppgiften,
det vill säga när det är oklart hur eleverna ska angripa uppgiften.
Sökord: begrepp, area, omkrets
Postadress
Växjö universitet
351 95 Växjö
Gatuadress
Universitetsplatsen
Telefon
0470-708000
2
Innehållsförteckning
1. INLEDNING ....................................................................................................................... 4
2. SYFTE................................................................................................................................... 6
2.1 FRÅGESTÄLLNINGAR......................................................................................................... 6
3. TEORETISK BAKGRUND................................................................................................ 7
3.1 LÄROPLAN OCH KURSPLAN ............................................................................................... 7
3.2 ELEVERS FÖRMÅGOR ........................................................................................................ 8
3.3 BASKUNSKAPER OCH BEGREPP .......................................................................................... 9
3.3 OMKRETS ........................................................................................................................ 11
3.4 AREA .............................................................................................................................. 12
3.5 BEGREPPEN I SAMSPEL .................................................................................................... 12
4. METOD .............................................................................................................................. 14
4.1 METODVAL ..................................................................................................................... 14
4.2 URVAL ............................................................................................................................ 14
4.3 GENOMFÖRANDE ............................................................................................................ 15
4.4 ETISKA ASPEKTER ........................................................................................................... 16
4.5 VALIDITET ...................................................................................................................... 16
4.6 RELIABILITET .................................................................................................................. 17
5. LÄROMEDELSPRESENTATION.................................................................................. 18
6. RESULTAT OCH ANALYS ............................................................................................ 19
6.1 DIAGNOSRESULTAT ........................................................................................................ 19
6.1 KVALITATIV ANALYS AV ELEVLÖSNINGAR ..................................................................... 22
6.2. PRESENTATION AV INTERVJUFRÅGOR ............................................................................ 23
6.3 INTERVJURESULTAT ........................................................................................................ 23
6.3.1 Vad innebär begreppet omkrets? ............................................................................ 24
6.3.2 Vad innebär begreppet area? ................................................................................. 24
6.3.3 Finns det någon skillnad på omkrets och area? ..................................................... 26
6.4 ANALYS .......................................................................................................................... 27
7. DISKUSSION..................................................................................................................... 30
7.1 LÄRANDESITUATIONEN ................................................................................................... 30
7.2 SPRÅKET ......................................................................................................................... 32
7.3 AVSLUTANDE REFLEKTIONER ......................................................................................... 33
8. KÄLLFÖRTECKNING .................................................................................................... 35
Bilaga 1 Diagnos ............................................................................................................. 36
Bilaga 2 Intervjuer........................................................................................................... 39
Bilaga 3 Brev till föräldrarna .......................................................................................... 48
3
1. Inledning
Inom matematiken myllrar det av begrepp där dagens elever måste ha en viss kunskap för att
kunna hantera beräkningar och liknande. Redan tidigt i skolans värld börjar vi diskutera och
arbeta med elevernas begreppsuppfattning och hur vi på bästa sätt stödjer den. Att förstå att
siffran 2 står som symbol för just antalet två är inte helt självklart. Kronqvist och Malmer
påpekar i sin bok Räkna med barn (1993) att det finns olika sätt att ge uttryck för ett talvärde.
Detta är till exempel
•
att referera med hjälp av verkliga föremål, exempelvis stenar
•
att muntligt eller skriftligt uttala räkneord
•
med hjälp av symboler som kan vara siffror, men även bokstäver exempelvis i det
romerska talsystemet
Det är heller inte helt självklart vad till exempel begreppet cirkelskiva innebär. Detta är ett av
många begrepp som eleverna i skolår 1-3 möter och ska bilda sig en uppfattning om
(Ahlström m.fl., 2001). Ju längre vi kommer i skolmatematiken, desto mer komplexa
begrepp. Två begrepp som för oss känns välkända, är omkrets och area. Dessa begrepp stöter
eleverna på efter ett par år i skolans värld och de förekommer sedan med jämna mellanrum
och med varierande svårighetsgrad. Frågan är vilken reell kunskap eleverna har kring dessa
begrepp? Vad betyder de? Hur skiljer eleverna dem åt?
När vi läser om undersökningar som gjorts efter år fem i grundskolan möter vi påpekanden
om vanligt förekommande missuppfattningar gällande just omkrets och area (Unenge, 1998).
Eleverna verkar kunna hantera begreppen när endast ett av dem introducerats. När de båda
begreppen samspelar i exempelvis läromedel tror vi att det kan ställa till stora problem för
många elever. Frågan vi ställer oss är om dessa missuppfattningar kring begreppen area och
omkrets uppstår och i sådana fall, varför gör de det? Vårt arbete kommer att fokusera på just
detta, som inom matematikdidaktiken anses vara ett vanligt förekommande diskussionsämne.
Elever sägs missuppfatta begreppen och/eller relationen mellan area och omkrets. Därför vill
vi skaffa oss kunskap om det verkligen är så att det existerar en missuppfattning, och vad det i
så fall rör sig om. Vilka faktorer är det som gör att denna missuppfattning är så utbredd?
4
När vi har varit på VFU på olika skolor har vi sett just begreppsbildning som en stor del av
matematikundervisningen, och att det är ett väldigt komplext uppdrag som ingår i vår
lärarprofession. Just inom area och omkrets har vi sett att eleverna ibland stöter på problem,
men vi har aldrig fått chansen att ta reda på vad problemen har sin grund i. Att verbalt
diskutera och reflektera kring area och omkrets kanske är något där vår undervisning brister?
Vi ska med denna uppsats försöka svara på dessa frågor, men även titta på de problem som
blir resultatet av detta. Anledningen till att vi valde att titta på just detta ämne är att vi både
tycker att just geometri är både ett roligt och viktigt område. Trots det väl kända dilemmat
kring elevers missuppfattningar finns väldigt lite forskning i frågan varför det uppstår
missuppfattningar. Vi tycker därför att det är väldigt intressant att undersöka ämnet vidare.
5
2. Syfte
Syftet med vårt arbete är att undersöka några elevers begreppsuppfattning inom området area
och omkrets. Vi vill ta reda på om det förekommer missuppfattningar, och i så fall, vill vi ta
reda på hur missuppfattningarna ser ut. Vi vill granska vad som skulle kunna ligga till grund
för elevernas eventuella missuppfattningar och vad vi, som blivande lärare i matematik, kan
göra åt dem. Vi hoppas få ett bredare underlag att jobba med då vi diagnostiserar elever från
två skolor i skolår sex. Syftet är också att försöka se huruvida läromedelsvalet påverkar våra
elever inom det här arbetsområdet.
2.1 Frågeställningar
Vilka kunskaper har eleverna i skolår sex kring begreppen area och omkrets?
Vilka missuppfattningar förekommer gällande begreppen area och omkrets i de aktuella
klasserna?
Vad ligger bakom de eventuella missuppfattningarna?
6
3. Teoretisk bakgrund
Allt fler elever går ut grundskolan med bristande matematikkunskaper idag, jämfört med för
bara 10 år sedan (www.skolverket.se). När man idag ser på de elever som kommer till
gymnasiet efter att ha gått ur grundskolan blir man ibland lite förvånad. Många elever har
problem med de mest vardagliga delarna inom matematiken. På Skolverkets hemsida
(www.skolverket.se) kunde man den 20 nov (2007) läsa att allt färre elever når målen i
matematik. Andelen behöriga till gymnasieskolan minskade från 91,4 procent år 1998 till
89,2 procent år 2007.
Drygt åtta procent inte godkända i matematik. Av de enskilda ämnena är det
8,5 procent som inte når målen i matematik vilket är högre än förgående år.
Motsvarande andelar för engelska är 7,3 procent, för svenska 4,7 och för
svenska som andraspråk 24,1 procent vilket är i stort sett samma andel som
tidigare.
(www.skolverket.se)
3.1 Läroplan och kursplan
I läroplanen för grundskolan (Lpo 94) finns det flera kunskapsmål att sträva mot och uppnå
inom matematiken. Läroplanen påpekar att skolan ansvarar för att varje elev efter
genomgången grundskola:
•
utvecklar nyfikenhet och lust att lära,
•
utvecklar sitt eget sätt att lära,
•
utvecklar tillit till sin egen förmåga,
•
behärskar grundläggande matematiskt tänkande och kan tillämpa det i vardagslivet
(s.9, 11)
Att just utvecklas är en viktig del i grundskolan och speciellt i matematiken där man hela
tiden utvecklar sitt tänkande och bygger vidare på det man redan kan. I kursplanen för årskurs
fem inom matematiken, finns mål att uppnå efter skolår fem och mål att sträva mot. Inom
geometrin finns följande mål att uppnå:
Eleven ska
•
ha en grundläggande rumsuppfattning och kunna känna igen och beskriva några
viktiga egenskaper hos geometriska figurer och mönster
7
•
kunna jämföra, uppskatta och mäta längder, areor, volymer, vinklar, massor och tider
samt kunna använda ritningar och kartor
De mål de ska sträva mot är följande:
Eleven ska ha
•
förmåga att förstå och använda olika metoder, måttsystem och mätinstrument för att
jämföra, uppskatta och bestämma storleken av viktiga storheter
•
förmåga att förstå och använda grundläggande geometriska begrepp, egenskaper,
relationer och samband
(Skolverket, Mål i matematik för grundskolan)
3.2 Elevers förmågor
Grundskolans läroplan diskuterar på olika sätt vilka förmågor och kompetenser vi ska vägleda
våra elever till. I det här avseendet är det viktigt att vi har en gemensam bild av vad kunskap
är. Fyra olika komponenter inom kunskap anges ofta med utgångspunkt i Lpo94;
-
fakta
-
färdighet
-
förståelse
-
förtrogenhet
Unenge (1998) gör efter dessa fyra F en uppdelning i fyra elevkategorier. Elevkategori ett kan
som svar på konkret fråga ge svar/påstå att arean beräknas genom att multiplicera längd och
bredd på den aktuella figuren, vilket kan stämma i vissa fall. Elevkategori två kan visa
färdighet vad gäller att beräkna arean på en bestämd yta, t.ex. en rektangel. Den tredje
kategorin kan med ord förklara hur vi beräknar arean, och hur vi hanterar mätetal, vid
redovisning av formler som gäller i sammanhanget. Elevkategori fyra har förmåga att verbalt
förklara begreppet area (generellt) och även förklara hur man kan beräkna arean av en
oregelbunden figur. Kategorierna av elever som hamnar i grupp tre eller fyra besitter något
som Unenge i sammanhanget kallar för den tysta kunskapen. Denna efterfrågas sällan i
skolans värld och våra kunskapsmätningar bygger ofta på att elevkategori ett och/eller två har
fördelar. Eleverna måste kunna sätta ord på och reflektera kring matematiska dilemman,
särskilt när de utför fler räkneoperationer med hjälp av miniräknare och/eller datorer. Då blir
8
kategorierna med faktakunskapen inte längre så viktiga, eftersom våra datorer utför den
handlingen åt oss. Naturligtvis kan eleverna bemästra en eller flera av kategorierna, men vårt
strävansmål borde vara att alla elever klarar samtliga fyra kategorier, inom area och omkrets
(Unenge, 1998).
3.3 Baskunskaper och begrepp
För att kunna hantera matematiken i de senare åren måste man ha en stadig grund att bygga
på. Denna grund brukar man kalla för baskunskaper, och har man bristande eller rent av
saknar dessa kunskaper, blir matematiken i skolan en svår uppgift. Om baskunskaper pratar
Löwing och Kilborn i boken Baskunskaper i matematik. De delar upp baskunskaperna i tre
olika områden, nämligen:
•
Nödvändiga kunskaper i matematik för hem och arbete
•
Nödvändiga kunskaper i matematik för arbete med andra skolämnen
•
Nödvändiga kunskaper för vidare studier i matematik
När det gäller att veta hur man räknar med omkrets och area är denna baskunskap angelägen i
både punkt ett och tre. Om eleverna inte har goda baskunskaper i matematiken kommer
framförallt punkt tre att bli väldigt lidande. I dagens Sverige, när alla elever läser minst
matematik A på gymnasiet, så är denna typ av kunskap viktig att behärska (Löwing och
Kilborn, 2002).
Författarna menar också att man för att lära sig och tillägna sig dessa baskunskaper är det
väldigt viktigt att vi förstår vad vi pratar om. Man hör ofta utryck som att vi ska ”tala
matematik” och att ”matematik är ett språk”. I de tidiga åldrarna kommer man ganska långt
med sitt vardagsspråk, men när matematiken blir lite mer abstrakt kan man inte använda sig
av sitt vardagliga språk i alla moment. När nya begrepp presenteras är det viktigt att läraren
går framåt väldigt försiktigt. Det är viktigt att dessa begrepp konkretiseras och att eleverna
genom samtal och diskussioner lär sig hur dessa nya begrepp blir ett komplement för
vardagsspråket. Om eleverna inte lyckas med detta finns en risk att matematiken bara blir
skolinriktad och de klarar inte av att upptäcka i ”vardagens många valsituationer” (Kilborn,
2002).
9
När man tittar på alla begrepp och ord som finns inom matematiken är det lätt att förstå att
ämnet inte bara innebär räkning. I publikationen Matematik – ett kommunikationsämne
(2001) tar författaren upp ord och begrepp som förekommer inom geometrin för grundskolan.
Här finns ungefär 200 ord som alla förekommer inom just geometrin. Då eleverna enligt
kursplanen ska kunna kommunicera matematik i meningsfulla och relevanta situationer
behöver eleverna få möjlighet att lära sig och kunna behärska just det matematiska språket
och dessutom många av de ord som hör till.
Eriksson (2001), som är en av författarna till skriften Matematik – ett kommunikationsämne,
menar att begreppsbildningen går snabbare i ett socialt sammanhang. Begreppsbildningen
sker mer effektivt när eleverna får arbeta i par eller grupp jämfört med individuellt arbete.
Om ett begrepp som en elev inte känner till dyker upp är det inte ovanligt att någon annan i
gruppen vet vad det betyder och kan då förklara innebörden. På detta sätt lär sig eleverna att
genom samtal förklara och samarbeta med varandra, både för att öka begreppsuppfattningen
samt för att komma fram till svaret på en uppgift.
När det gäller just geometrin är en viktig förutsättning för baskunskap att man lär sig begrepp.
För att kunna resonera vidare krävs att vi definierar ordet begrepp. En förklaring, från
Nationalencyklopedin, lyder som följer;
Det abstrakta innehållet hos en språklig term till skillnad från dels termen
själv, dels de objekt som termen betecknar eller appliceras på.
Med begreppet stad t.ex. avses således den innebörd vi lägger i uttrycket
´stad´, vilket måste skiljas från såväl ordet ´stad´ som de geografiska
orter som betecknas som städer.
(Nationalencyklopedin 2005)
Vissa begrepp kan man lära sig direkt från den vardagliga miljön, men när det kommer till lite
svårare begrepp måste man ha hjälp av en matematiker (Skemp, 1987). Det är vi lärare som är
dessa matematiker när vi lär våra elever. När eleverna lär sig nya begrepp är det väldigt
viktigt att vi som undervisar förstår dem väl och kan använda dem. Begreppet i sig kan verka
väldigt enkelt men för en elev som aldrig sett det tidigare betyder varje nytt begrepp mycket
tänkande, menar Skemp (1987). När läraren undervisar kring nya begrepp kan hon/han inte
bara göra detta med hjälp av en definition, man måste även använda sig av flera lämpliga
exempel. Detta är svårare än det låter då alla exempel måste bygga på och tillämpa begreppet
10
man jobbar med. Om man som lärare inte ger bra och givande exempel blir det svårt för
eleverna att ha något speciellt att hänga upp kunskapen på när det gäller den nya delen de just
börjat jobba med (Skemp, 1987).
Unenge (1988) menar att det framför allt inom geometrin krävs ordning och reda bland
begreppen, samt att vi bör ta tillvara på den logik som är relevant. Det är viktigt att hålla isär
vad som är definition och vad som gemensamt kan resoneras fram. När eleven själv får chans
att lära sig ett nytt begrepp genom att resonera fram och/eller upptäcka sammanhang och
helhet, blir kunskapen mer bestående. Detta påpekar även Eriksson (2001). Han skiljer mellan
deduktiv respektive induktiv metod när det gäller begreppsbildning. Dessa kan i vardagliga
termer beskrivas som ”förklarande” samt ”upptäckande” metoder. Han framhåller elevens
vardagliga upptäckande verksamhet, där pedagogen utgår från elevens verklighetsbild och
tidigare erfarenheter.
3.3 Omkrets
Begreppet omkrets definieras som följer;
En enkel sluten kurva i ett plan begränsar ett område och
längden av kurvan kallas kurvans eller områdets omkrets.
(Unenge, 1998, sid.152)
Att beräkna en figurs omkrets är något som eleverna är vana vid, även om de som sagt har
problem att hålla isär de två olika begreppen area och omkrets. I en undersökning, som
Unenge hänvisar till i sin bok Lära matematik (1998), där ett samtal mellan lärare och elever
spelats in och transkriberats, inträffar följande;
Läraren visar en sexsidig figur där måtten är utsatta i cm. Hon ställer frågan Vad säger ni om
det här? Det svar hon allra först får är Det blir 23, vilket är summan av de sex siffrorna när
man adderar dem. Hon har alltså vid det här tillfället inte bett eleverna att räkna ut något. I
diskussionen framkommer att eleverna automatiskt använder räknesättet addition när det
förekommer fler än två siffror i en känd figur. Att eleverna genast drar denna slutsats är
kanske en kombination av vana vid en viss typ av uppgift, och resonemang kring vilka
möjligheter som är rimliga. Det säger dock en hel del om de strategier som eleverna använder
sig av inom matematiklektionerna. Samma lärare fortsätter senare vid ett annat tillfälle att ge
11
eleverna en bestämd omkrets på en sexhörning och frågar hur figuren kan se ut. Eleverna fick
sedan ”laborera fram” hur figuren kunde se ut. Unenge menar att eleverna på detta sätt stärker
uppfattningen kring begreppet omkrets (1998).
3.4 Area
Vad betyder egentligen ordet area? Vad innebär begreppet inom matematiken? En
matematisk förklaring lyder som följer;
Arean av en begränsad yta, t.ex. ett begränsat område, är ett mått på dess
storlek.
Som areaenhet tas arean av ett kvadratområde med enhetssträckan som sida.
(Unenge, 1998, sid.154)
Ett problem Anderberg (1992) beskriver, är att missuppfattningar är vanliga när man ska
beräkna area och omkrets på månghörningar. Dessa kan ha samma omkrets men olika areor
och tvärt om. När elever hör uttrycket area, tänker de ofta på kvadrater eller rektanglar,
eftersom det är det de flesta uppgifterna de räknar med behandlar. Genom att använda sig av
områden som har fler är fyra sidor anser Anderberg att man kan stärka just areabegreppet.
Öberg (1998) menar att våra elever egentligen har en ganska klar uppfattning kring area och
vad det är. Skolan har dock via sina arbetsmetoder kringgått den kunskap som eleverna har,
och istället för att knyta an till den kunskap eleverna redan har med sig, har man tagit ett helt
nytt kapitel för eleverna. På detta sätt har man misslyckats med att anknyta till elevernas
tidigare erfarenheter. Vi brister i att förena skolans innehåll med elevernas vardagliga
upplevelser (Malmer, 1991). Detta resulterar i att eleverna har dubbla kunskaper, dels det vi
använder vid beräkningar i skolan, dels sin vardagskunskap, men utan relevant benämning.
Begreppet area existerar dessutom näst intill endast inom matematikundervisningen (Unenge,
1998).
3.5 Begreppen i samspel
I boken Lära matematik (Unenge, 1998) står att läsa om flera undersökningar som gjorts i
frågan gällande elevers eventuella missuppfattningar kring begreppen area och omkrets, efter
att båda begreppen introducerats. Att missuppfattningarna existerar menar Unenge att det inte
råder några tvivel om, men vad beror missuppfattningarna på, och hur ser de ut? Omkrets och
12
area tillhör matematikens baskunskaper och en relativt stor del av undervisning inom
matematik bygger på att eleven i fråga har kunskap och förmåga att använda begreppen
korrekt. Det visar sig i forskning att efter att de båda begreppen introducerats har eleverna
svårt att skilja dem åt. Likaså har eleverna svårigheter i att ange rätt enhet.
När man räknar inom geometrin är det viktigt att eleverna bygger sina kunskaper på en fast
begreppsbildning menar Bengt Anderberg, som är en av de medverkande i boken Geometri
och statistik (1992). Han instämmer med Unenge och menar att ”det är inte ovanligt att
elever blandar ihop omkrets och area”. Just vid beräkningar av area förstår inte elever varför
cm٠cm blir cm2 och när man räknar omkrets blir det bara cm. Ett exempel han ger är att om
man multiplicerar kronor med varandra, dvs. kr٠kr blir det då kr2 och vad betyder detta i
sådana fall?
Även Unenge menar i sin bok Matematikdidaktik för grundskolan (1988) att ett problem inom
areabegreppet är just multiplikationen av enheten. Det handlar inte bara om själva begreppet
area, eleven ska också kunna beräkna area. Båda problemen är omfattande, vilket enligt
Unenge därför borde göras en sak i taget. Det innebär rimligtvis att begreppet kommer först.
Den forskning som tidigare gjorts har alltså enligt Unenge visat att eleverna egentligen har
förmåga att beräkna kroppars/figurers omkrets. Det är först när de båda begreppen ska
samspela som eleverna får problem. I en studie som gjorts i skolår sju, visar resultaten på
stora brister inom kunskapsområdet. Som exempel kan anges att hela 11 % av eleverna som
utfört testet, anser att det inte går att räkna ut en area på en bestämd oregelbunden figur.
Dessutom är det 41 % som helt avstår från att svara på frågan, och ytterligare 11 % som
beräknar uppgiften på helt fel sätt. 30 % av eleverna räknar ut figurens omkrets. Visserligen
sägs eleverna vara ovana vid den här sortens uppgifter, men om det är sant, innebär det då
inte att vi förbereder våra elever på en viss sorts uppgifter?
Ett liknande resultat infinner sig under 2006, då NCM: s årliga matematiktävling Ecolier, som
är avsedd för skolår tre och fyra, går av stapeln. En figur i ett rutmönster där eleverna ska
räkna ut dess area, ställer till stora problem. På denna uppgift var lösningsfrekvensen cirka
20%. Men det var inte ett utslag av "blind gissning". Det fanns ett mönster i de vanligaste
svaren: De flesta hade svarat alternativ C. När det gällde alternativ A och E hade ungefär lika
många svarat (se uppgift 8 i diagnosen).
13
4. Metod
4.1 Metodval
För att få ett så bra och rättvist resultat som möjligt i detta arbete valde vi att göra både en
diagnos och sedan intervjuer. På detta sätt kommer vi att kunna ha både en kvalitativ del och
en kvantitativ del i uppsatsen. Då dessa två metoder kompletterar varandra, enligt Jacobson
(2002) är detta en bra utgångspunkt. Genom att skaffa sig kunskap från den kvantitativa
undersökningen kan man sedan utforma ett bättre frågeformulär, menar han också. Då en
kvantitativ undersökning inte alltid ger helt klara svar kan sedan en intervju göra att man kan
undersöka svaren djupare och på detta sätt komplettera undersökningen på ett kvalitativt sätt
(Ibid.). För att få ett bra resultat i en undersökning är en kvantitativ del (som till exempel en
diagnos) en nödvändighet. Att bara titta på själva intervjun som ett sätt att samla in data
menar Jacobson att detta sätt är bra då det lägger vikt vid detaljer samt att man får fram det
unika med varje person som intervjuas.
4.2 Urval
Bryman (2002) menar att grunden av samtliga enheter varifrån man gör sitt urval är
populationen och utifrån den väljer man sedan ut den metod som passar bäst för
undersökningen. Då det bara finns två klasser i skolår sex på de skolor vi valt att arbeta med
betyder det att vi kommer att titta på hela populationen av de berörda eleverna i detta fall.
När alla eleverna har gjort en diagnos sammanställer vi den och gör därefter vad Bryman
kallar ett stickprov eller sampel. Vi väljer alltså ut en del av populationen för att intervjua
dessa elever. Vi kan nu använda oss av vissa frågor där vi ser att många elever har svarat fel
eller rätt för att få en bättre förståelse för varför eleverna svarat som dem gjort på diagnosen.
Detta menar Bryman leder till en större reliabilitet. Genom att låta eleverna göra diagnosen
innan intervjun vet de som vi talar med ungefär vad vi kommer att fråga de. På detta sätt
kommer vi att få bättre och mer väsentliga svar från eleverna på de frågor vi har. Både elever
som inte uppvisar förståelse för begreppen, samt elever som verkar ha förståelse och kunskap
kring area och omkrets, kommer att väljas ut.
14
4.3 Genomförande
Innan vi börjar vår undersökning ger vi eleverna ett brev där vi talar om att de ska bli
intervjuade, detta för att få målsmans godkännande (se bilaga 3). Vi inleder med att göra en
diagnos för att se hur kunskapen ser ut bland våra aktuella elever. Vi lägger in olika slags
uppgifter i diagnosen, för att se huruvida en viss formulering eller frågeställning ställer till det
för vissa elever. Anledningen till att vi låter alla elever göra diagnosen är för att vi ska få en
övergripande uppfattning om vilka av uppgifterna som har skapat problem för eleverna. Den
här delen av vår undersökning är kvantitativ, eftersom vi med hjälp av metoden prövar en av
våra frågeställningar (Bryman, 2002). För att ta reda på vad som ligger bakom deras svar och
vilka lösningsstrategier de använt sig av är intervjuer väldigt viktiga i vårt arbete. Vi kommer
att på detta sätt kunna gå djupare in i elevernas tänkande och försöka förstå varför de har
svarat på olika sätt på diagnosen som de tidigare gjort. Då vi tittar på hur missuppfattningar
sker är det väldigt viktigt att eleverna får förklara hur de har tänkt när de löste uppgifterna
både uppgifter de svarat rätt och fel på. När man bara tittar på ett svar är det väldigt svårt att
förstå varför en elev har svarat på ett visst sätt. Då eleven själv får förklara ger detta oss en
mycket djupare förståelse för hur de har tänkt när de kom fram till sitt svar på de olika
uppgifterna.
Vi kommer att genomföra kvalitativa intervjuer med eleverna. Kvalitativa intervjuer innebär
att fokus ligger på den intervjuades åsikter, medan den kvantitativa undersökningen speglar
forskarens intresse. En fördel med just denna intervjuteknik är att den som blir intervjuad kan
svara med egna ord och om dem inte förstår vad som menas kan de få hjälp av intervjuaren
menar Bryman (2004). Vi kommer att genomföra våra intervjuer i ett enskilt grupprum, där
eleven i lugn och ro kommer att få svara på våra frågor. Då vår intervjuguide bygger på
diagnosen har vi inte så många frågor utan kommer mestadels att utgå ifrån diagnosen. Vi
kommer att använda oss av en semistrukturerad intervjuform, för att kunna anpassa våra
övergripande frågeställningar till elevernas svar, och även till elevernas kunskapsnivå. Detta
innebär också att frågorna som ingår, kan komma i annan ordning än vad som står i
intervjuguiden. Denna intervjuprocess är flexibel (Bryman, 2004), på så sätt att vi inte
fokuserar på huruvida eleven svarar ”korrekt” på våra frågor, utan vad eleven själv upplever
som viktigt vid förklaring och förståelse vid svaren. Intervjuerna spelas in, för att sedan
15
transkriberas och granskas. Med all samlad information kommer vi sedan att dra slutsatser
kring frågeställningen. Vi kommer även att titta på de läromedel läraren använt sig av då det
gäller undervisningen inom arbetsområdet geometri, för att försöka se om det finns några
väsentliga skillnader.
4.4 Etiska aspekter
När undersökningar genomförs dyker etiska dilemman upp (Jacobsen, 2002). Dessa uppstår
först och främst i situationer där vi, av metodiska skäl, vill dölja avsikten med en
undersökning för den som undersöks. Om personer som är involverade i en undersökning
undanhålls en avsikt kan detta leda till att tillförlitligheten hotas. När man arbetar med en
undersökning brukar det finnas tre grundkrav som denna måste uppfylla menar Jacobsen.
Dessa är informerat samtycke, krav på privatliv och krav på korrekt återgivning.
Den grundläggande förutsättningen för informerat samtycke är att den som utfrågas/intervjuas
frivilligt deltar i undersökningen. Lika viktigt är det att sedan låta den undersökta inneha och
bibehålla sin frizon. Det vill säga att individen har rätt till ett privatliv och detta ska inte
undersökas. Det tredje och sista kravet är att allt återges korrekt, och det innebär att inget får
förfalskas och att inte heller presentera felaktiga resultat
I den här undersökningen syftar detta till att vi bett om målsmans underskrift för att godkänna
elevernas deltagande, men naturligtvis även elevens eget samtycke. Vi inleder varje
intervjusituation med att påpeka för den aktuella eleven att inget av det som sägs i intervjun
kommer att kunna kopplas till individen eller skolan. Dessutom presenteras det i ett anonymt
sammanhang.
4.5 Validitet
Validitet är en bedömning om de slutsatser som genererats från en undersökning hänger ihop
eller inte (2004). Det finns flera olika sätt att bestämma validiteten. Den som är vanligast när
man använder sig av kvalitativ forskning är begreppsvaliditet. I grunden handlar det om
frågan huruvida ett begrepp verkligen speglar det som begreppet anses beteckna. I den
litteratur vi använder oss av hittar vi stöd för att elever missuppfattar just begrepp som area
och omkrets.
16
4.6 Reliabilitet
När en undersökning genomförs är det viktigt att reliabiliteten eller tillförlitligheten är hög.
Med reliabilitet undrar man om resultatet från en undersökning blir samma om man genomför
undersökningen igen, eller om den påverkas av slumpmässiga eller tillfälliga betingelser.
Vi anser att de svar vi kommer att få fram av eleverna när de genomför diagnosen är
tillförlitliga, då eleverna vid diagnostillfället kommer att genomföra den självständigt, utan
hjälp från någon. När vi sedan ska intervjua eleverna kommer vi att förhålla oss till dem på ett
sådant sätt att vi inte styr deras svar i någon riktning. Detta anser vi ska ge oss ett tillförlitligt
resultat. Då det gäller hela undersökningen är det bara en liten begränsad population som vi
genomfört den på så därför kan inte resultatet räknas som ett generellt resultat för alla elever.
17
5. Läromedelspresentation
De skolor där vi gjort våra intervjuer använder sig av läromedlet Matteborgen (Bonniers). I
Matteborgen 5A presenteras areabegreppet för första gången. Det sker med hjälp av en
mosaikbit, i form av en kvadrat med sidan 1cm. Därefter får eleverna räkna antal bitar i olika
sammansättningar. De får veta att en mosaikbit har arean 1 cm2. I lärarhandledningen
motiverar man detta genom att detta ska skapa en god förståelse för areabegreppet.
Författarna anser att det i detta sammanhang är viktigt att eleverna får repetera skalbegreppet
och omkrets. I samband med det här finns efter varje kapitel i boken en diagnos på området.
För de elever som har svårt att befästa begreppen i kapitlet finns Rustkammaren, där
repetitionsuppgifter finns. De elever som klarar diagnosen kan fortsätta till kapitlet Tornet,
som innehåller lite svårare uppgifter, där författarna anser att eleverna behöver tänka till lite
extra. Kapitlet Tornet är placerat före repetitionsuppgifterna, något som författarna menar kan
förebygga tävlingsmomentet med att ”ligga först” i matteboken. Detta kapitel är det enda där
begreppen area och omkrets förekommer för skolår 5. Författarna anser att eleverna, efter att
ha räknat Matteborgen 5A och 5B, ska klara uppnåendemålen i skolår 5.
I Matteborgen 6A dyker begreppen upp igen. Först sker en repetition av både omkrets och
area, på ca tio uppgifter vardera. Författarna syftar i areadelen till att eleverna ska skapa en
förståelse för att en kvadratmeter eller en kvadratcentimeter inte måste ha formen av en
kvadrat. Här finns också uppgifter där eleven ombeds att välja rätt enhet. Efter repetitionen
introduceras triangelns area, då även begreppen bas och höjd (som då visas både för rektangel
och för triangel). Skillnaden från Matteborgen 5A är att man i bok 6A anser att eleverna bör
hinna med uppgifter i både Rustkammaren och Tornet. Författarna menar dock att eleverna
inte behöver göra alla uppgifterna i kapitlet, det är snarare bättre att eleven får chans att
försöka på de lite svårare uppgifterna. Efter dessa uppgifter finns en sammanfattning av
kapitlet, därefter följer en så kallad utmaning. Denna består av lite klurigare uppgifter, som
hänger samman med kapitlet. Författarna anser att denna med fördel görs i grupp. Varje gång
då area eller omkrets förekommer i läromedlet, kommer först ett antal uppgifter gällande
omkrets, och därefter ett antal uppgifter som behandlar area. Begreppen behandlas parallellt
och tillsammans i samtliga kapitel där de förekommer. Öppna uppgifter förekommer sällan
utan de är ofta styrda på sådant sätt att den konkret efterfrågar area eller omkrets.
18
6. Resultat och analys
6.1 Diagnosresultat
Vi har låtit 28 elever, i två olika klasser, göra diagnosen. Efter att ha rättat diagnoserna ser vi
att missuppfattningar kring begreppen förekommer. Detta innebär att vi här har besvarat en av
våra övergripande frågeställningar, angående om det förekommer missuppfattningar. För att
ytterligare undersöka vad som ligger bakom detta har vi använt diagnoserna som ett underlag
när vi valt ut vilka elever vi ville intervjua. Här nedan följer ett sammanställt resultat av
elevernas svar på diagnosen.
Antal elever
Diagnosresultat
30
20
Antal rätt
Antal fel
10
0
1
2 3
4 5
6 7 8
9 10 11
Uppgift
Här följer svarsfrekvensen fråga för fråga:
1. Kan du rita en figur och visa hur du räknar ut omkretsen?
28 elever svarar korrekt.
2. Kan du rita en figur och visa hur du räknar ut arean?
24 elever svarar rätt. 4 elever svarar fel. Två av dem gör ytterligare en rektangel och räknar än
en gång ut omkretsen. Två elever svarar med rätt tal men med fel enhet.
3. Rita två olika rektanglar med omkretsen 18 cm.
19 elever svarar rätt. 9 elever svarar fel. Här varierar svar mellan att ändra omkretsen,
19
till att svara att det inte går.
4. Rita två olika rektanglar med arean 18 cm2
16 elever svarar rätt. 12 elever svarar fel. 8 av dem säger att det inte går. 4 elever försöker
men räknar helt sonika ut omkretsen igen.
5. Vad ska stå efter talet på raden? Välj bland enheterna i rutan.
a) Ett sovrums area kan vara 17 _____
cm2
b) En tavlas omkrets kan vara 300 _____
m2 cm
c) Arean av en dörrmatta är ungefär 24 _____
d) Översidan på en tändsticksask är ungefär 19 _____
mm2
dm2
m
dm
21 elever svarar med högst ett fel. 7 elever svarar med fler än ett fel. 1 elev visar ingen som
helst förståelse för frågan. 2 elever hoppar över frågan (intervjuar en av dem som säger att
han inte orkade). 4 elever gör fel på två eller fler. Vanligt är att det handlar om att missa
kvadrattecknet.
6. Går det att göra två figurer som har samma omkrets men olika area? I sådana fall visa
hur. Ledtråd: tänk dig att du har ett 20 cm lång snöre och knyter ihop ändarna, kan du då
göra olika figurer? Har dessa figurer lika stor area?
22 elever svarar rätt. 6 elever svarar fel. De som svarar fel skriver att arean alltid är den
samma, alltså 20 cm2.
7. Beräkna figurens omkrets och area.
20
19 elever svarar helt korrekt. 9 elever svarar fel. 3 elever hoppar över uppgiften. Det
vanligaste felet är att ta 3 gånger 2, eller 4 gånger 2.
11 elever svarar rätt. 17 elever svarar fel.
8.
11 elever svarar rätt. 17 elever svarar fel.
9. Vilket område är störst?
26 elever svarar rätt. 2 elever svarar fel.
10. Kan du genom att rita i figuren och skriva berätta hur du skulle bära dig åt för att räkna
ut arean på denna figur?
21
5 elever svarar rätt på frågan. 23 elever svarar fel. 13 elever svarar att det inte går, p.g.a.
figurens form. 2 elever försöker, men misslyckas vid uträkning. 3 elever ritar en fyrkant
ovanpå så nära som är möjligt och menar att man kan räkna ut arean i fyrkanten och sätta
”ungefärligt likhetstecken” framför. 5 elever svarar inte.
11. Beräkna arean på triangeln:
19 elever svarar rätt. 9 elever svarar fel. 3 elever glömmer att dividera med två, varav en vid
intervju inte ”vet” att man ska göra det. 6 elever hoppar över frågan.
6.1 Kvalitativ analys av elevlösningar
I vår kvalitativa resultatanalys har vi tittat på enstaka elevers svarsalternativ på
diagnosuppgifterna. Vi väljer att se närmare på tre av frågorna som kan ses som en
sammanfattning av vår diagnos.
På fråga 8 uppger någon elev att det var en gissning. Här förekommer ofta C som
svarsalternativ. Sambandet med svarsalternativ C är att figurerna innehåller samma antal
rutor. Då denna uppgift är direkt kopierad från NCM:s Kängurutävling ska den ses som
anpassad efter åldersgrupp och kunskapsnivå. Uppgiften är plockad ur Ecolier 2006, som är
avsedd för skolår 3-4. Vi har haft kontakt med NCM och ansvariga för Kängurutävlingen, där
vi fick veta att svarsfrekvensen då låg på ca 20 %. I vår genomförda diagnos ligger
svarsfrekvensen på ca 40 %.
På fråga 9 ber vi eleverna att tala om vilken av de tre figurerna som har störst area. När vi
konstruerade diagnosuppgiften valde vi att göra en av figurerna med större omkrets men dock
22
inte störst area. Detta för att få svar på huruvida eleverna har förståelse för och kan uppskatta
area. Svaren på frågan visar tydligt att eleverna i skolår 6 har god uppskattningsförmåga och
kan se vilken av figurerna som är störst. De två elever som inte svarar rätt på frågan har inte
svarat alls.
På fråga 10 framkommer många olika svarsalternativ, även om flertalet är fel. Några elever
menar att det är omöjligt att beräkna arean eftersom figuren är oregelbunden. De elever som
svarar rätt på frågan har antingen delat upp figuren i mindre delar, eller ritat en fyrkant
ovanpå figuren och visat en ungefärlig beräkning på hur man får figurens area.
6.2. Presentation av intervjufrågor
Vissa av frågorna där många av eleverna uppgett felaktiga svar anser vi vara intressanta att
diskutera med eleverna. Detta vill vi göra för att få djupare insikt i hur eleverna tänker, och
vilken kunskap som ligger till grund för deras svar. Vi ser tydligt att vissa av uppgifterna
vållar större bekymmer för fler elever. Då vi kommer att fråga eleverna om deras svar på
diagnosen har vi inte så många övergripande frågor. Vi vill här få reda på hur de har tänkt och
varför de har svarat som de har gjort på vår diagnos. Förutom frågorna vi har från diagnosen
vill vi även fråga dem om de tre frågorna nedan. Vad vi anser är viktigt är att vi får svar på de
frågeställningar vi ställde oss i början av arbetet.
1)
Vad betyder uttrycket omkrets?
2)
Vad betyder uttrycket area?
3)
Finns det någon skillnad på omkrets och area?
6.3 Intervjuresultat
Efter rättning av diagnoserna valde vi ut tre elever. Dessa valdes med utgångspunkt i att ingen
hade alla rätt, men inte heller alla fel. I och med att tyngdpunkten för vår undersökning är
kvalitativ är inga svar viktigare än andra. Vi vill undersöka elevers olika uppfattningar och
erfarenheter kring begreppen area och omkrets.
23
Vi har genom vår diagnos och de intervjuer vi har genomfört kommit fram till att det
förekommer stora kunskapsluckor hos eleverna vad gäller begreppen area och omkrets. Vi har
sett flera olika varianter när det gäller missuppfattningar och det saknas ofta en
verklighetsanknytning kring begreppen. Här nedan presenterar vi det resultat vi kommit fram
till i intervjuerna, en fråga i taget. Vi väljer även att presentera en del citat, där vi anser att
eleverna uttrycker bakgrunden till sina lösningar och även förklarar hur de har tänkt under
diagnosen.
6.3.1 Vad innebär begreppet omkrets?
Här finner vi att eleverna har god förståelse både vad gäller beräkning och uppfattning av
begreppet omkrets. Eleven i citatet nedan visar en vanlig uppfattning kring omkrets.
I: Här har du ritat en rektangel och räknat ut omkretsen. Hur tänkte du då?
E1: Jag tog och mätte varje sida, och sen plussade jag liksom ihop. 26 / Alltså blev det
tillsammans.
I: Mmm / 26?
E1: Ja, asså centimeter. Tror jag // eller ja, det är det.
Samma elev klarar också problemlösning när det gäller uppgifter som handlar om figurers
omkrets.
E1: Jaha, ja, man skulle ju ta två rektanglar, med samma omkrets. 18.
I: Ja. Hur tänkte du när du löste det här?
E1: Jag tänkte hur får jag 18 på olika sätt? Alltså så att allt tillsammans blir 18. Och då blev det
bara 4 plus 4 är 8, och så är det 10 kvar. Asså 5 på varje sida (pekar samtidigt på ”sin”
rektangel). Sen kunde jag komma på att 3 plus 3 är 6, och så blir det 12 kvar. 6 på varje sida.
Eleverna vi intervjuar har dock svårt att se hur en figur kan vara föränderlig, d.v.s. att samma
omkrets kan ge olika areavärden eller tvärtom. De verkar ovetande om att det förekommer .
6.3.2 Vad innebär begreppet area?
Samma elev kan med enkla ord beskriva vad area innebär, och hon har viss
verklighetsuppfattning som hon dock bygger på läromedlet.
24
I: Vad är area för något?
E1: Det är väl detta (pekar innanför rektangelns sidor)
I: Kan man förklara det på något sätt?
E1: Ehh, det är / det som får plats innanför strecken.
I: Ja, det kan man säga. När kan man ha nytta av att kunna räkna ut area?
E1: (funderar) I boken brukar det handla om att man ska mäta en bit jord eller så. Annars vet jag
inte redigt.
I: En bit jord?
E1: Jamen typ / en jordbit för grisar att gå på eller nåt.
Hennes kunskap och förståelse när det gäller enheten för areaberäkningar innebär att hon
känner till cm2 men hon kan inte förklara orsaken till enhetsbytet. Hon har också förmåga att
beräkna arean av en triangel men hon kan inte förklara varför hon dividerar med två.
I: Okej. Kan du räkna ut arean på triangeln här?
E1: Ja. 4 gånger 3 delat med 2 / 6.
I: 6?
E1: Ja. Det blir det.
I: Varför delade du med två?
E1: Därför att man ska det när det är en triangel.
I: Jaha. Vet du varför man ska dela med 2 då?
E1: // nä, det vet jag väl inte.
Elev 2 har förmåga att beräkna area när det gäller rektanglar. Han använder dock fel enhet i
sina svar. Han har stora svårigheter i sin förståelse vad gäller problemlösning kring area och
olika figurer. Han har ingen verklighetsanknytning som han kan uttrycka verbalt. När vi inte
frågar konkret efter areaberäkning har han svårt att se sambandet som uppgiften kräver. Han
klarar därför inte uppgifter där vi efterfrågar självständigt resonemang fram till att det ska
konkretiseras i form av areaberäkning.
E2: Man kan tro att det skulle bli (ohörbart) för det är samma rutor. Men snöret går ju att spänna
ut (spänner ut så långt det går). Man kan aldrig tro på area och sånt, det är alltid något lurt. I
boken är det jämt fyrkanter o så, det fattar jag, men inte varför det ska vara sånt här!
Han hänvisar själv till det aktuella läromedlet och ger senare uttryck för att han inte ser hur en
matematisk uppgift kan bygga vidare i flera steg. Han säger också att han känner sig ”lurad”
när uppgiften kräver lite mer. Elev 3 visar här nedan en större förståelse än föregående elev.
25
I: Ja, just det! Bra! Kan du visa hur du fick svaret på uppgift 10 också?
E3: Okej. Jag ritade en fyrkant så nära jag kan, och sen räknade jag bara arean på den. Så får
man ju skriva ett sånt där likamed-tecken som inte är liksom precis på pricken. Då fattar ju
Therese (läraren) att man visar att det är ungefär.
Här visar eleven att han är medveten om att även oregelbundna figurer har en area och han
uttrycker på ett enkelt sätt hur han skulle kunna göra en ungefärlig beräkning.
6.3.3 Finns det någon skillnad på omkrets och area?
Elev 3 har kunskap om hur han räknar ut både begreppet area och omkrets och kan även
verbalt förklara hur han använder sig av dessa begrepp. På detta sätt har han en djupare
förståelse. När figurerna blir oregelbundna får han däremot svårigheter men kan med lite
hjälp resonera sig fram till ett svar.
E3: Ja, jag räknade rutorna däri, och så la jag ut dom på en ny fyrkant.
I: Jag har ett snöre här som är lika långt, kan du passa in det och se om det är C som är rätt?
E3: Okej / (mäter) Nä / men / varför blir det den??
I: Ja, hur kan det bli det?
E3: Vet inte
I: Vad är det du har räknat när du räknat rutorna här inuti?
E3: / Ehh, jag vet inte / omkretsen / ?
I: Omkretsen vad är det?
E3: Hur långt det är / jaha! Jag har ju kollat hur mycket som får plats inuti! Men blir inte det
samma?
I: Mät så får vi se. Vilken av dom är rätt då?
E3: Ja, det är ju den. Men då ändras bara det inuti, och inte det runt om. Snöret är ju lika långt
ändå.
Eleverna vi intervjuat visar god förståelse när begreppen förekommer var för sig och frågan
konkret uttrycker vad det är som ska beräknas. När frågeställningen blir mer öppen känner
flertalet elever sig osäkra och begreppen förväxlas. Ett tydligt exempel på detta är elev 2 vi
intervjuat. Vid en frågeställning när intervjuaren inte talat om vad som bör beräknas har han
svårt att se samband och han kan inte koppla begreppen till sin vardag.
26
I: När man ska måla en vägg kanske? Så att man vet hur mycket färg som kommer att gå åt?
E2: Jamen då mäter man ju bara rakt om.
I: Hur då?
E2: Ja, hur långt det är runt om dörren. Så vet man ju.
I: Men vad är det vi mäter om vi mäter runt om dörren? Vi kan väl rita en dörr här på pappret.
E2: Mm. (ritar en rektangel)
I: Om vi mäter den här runt om, vad är det vi får fram då?
E2: Ja / hur mycket färg vi behöver för att måla den.
I: Och vad är det du har mätt?
E2: / hur lång dörren är.
Elevens uttalande innebär att han blandar ihop räknestrategierna och har svårt att förstå och
ge uttryck för vilken slags uträkning som bör göras när det gäller dörren. Han kommer inte
heller fram till något annorlunda i sitt svar trots en del följdfrågor.
6.4 Analys
I likhet med tidigare forskning inom ämnet, som Unenge presenterar (1998), uppvisar svaren
på vår diagnos att eleverna har kunskap och förmågan att beräkna omkrets. Alla elever som
gjort diagnosen har fått rätt svar på den första uppgiften (Rita en rektangel och räkna ut
omkretsen).
Genom intervjuerna har vi tydligt sett några av de olika kategorierna Unenge (1998)
beskriver. Han delar upp eleverna i fyra kategorier beroende på hur stor deras matematiska
kunskap är. Som ett exempel kan vi titta på elev 1. Hon kan både beräkna omkrets och area
och kan till viss mån förklara vad hon menar i ord. Hon pratar om ”jordbiten” som ett sätt att
använda sig av areaberäkning och hon känner även till att area är det ”innanför strecken”.
Enligt Unenges kategorier skulle då denna elev kunna kategoriseras som nivå tre. Hennes
baskunskaper är svaga, då hon inte fått befästa det hon lärt sig och hon saknar
verklighetsanknytningen vilket gör att hon får problem att tänka vidare inom området. Precis
som Kilborn (2002) påpekar blir hennes matematik endast skolinriktad och hon har svårt att
se nyttan av matematiken. När det gäller just areabegreppet har eleven svårt att räkna ut arean
på en oregelbunden figur, inledningsvis tror hon inte ens att det går. Anderberg (1992) menar
att just missuppfattningar kring beräknandet av månghörningarnas area kan leda till problem.
Genom att stärka elevernas kunskap på just detta skulle vi kunna undvika misstag menar
27
författaren. I detta påstående får Anderberg även stöd av Unenge (1998). Han menar att
eleverna genom att laborera med månghörningar stärker begreppsbildningen och förbättrar
sin kunskap. Vad han syftar på är att när elever ser en mångsidig figur med flera utsatta mått
tenderar de att räkna ut omkretsen, d.v.s. med hjälp av addition, utan att ens reflektera över
varför (1998).
En annan anledning till missuppfattningar är att det matematiska språket blir ett hinder. En
annan elev vi intervjuat misslyckas med uppgift tre på diagnosen och vid intervjun visar han
att detta beror på brister i det matematiska språket. Detta leder till att han inte förstår
uppgiften men när den förklaras för honom blir det tydligare och han klarar den till viss del.
Detta påvisar att eleven inte fått chans att konkretisera begreppen och han utför endast
mekanisk räkning. Som Kilborn (2002) påpekar är matematiken ett språk och det är viktigt att
eleverna lär sig att ”tala matematik”. Språket är en förutsättning för att matematiken ska
kunna utvecklas i ett socialt sammanhang. I boken Matematik – ett kommunikationsämne
(2001) skriver författaren att begreppsbildning går snabbare i samspel med andra, jämfört
med på egen hand. Genom att hjälpa varandra utvecklas eleverna, både vad gäller
begreppsbildning och uppgiftslösning.
Ett sätt att stödja elevernas matematiska utveckling är i valet av metod. Eriksson (2001)
förespråkar att vi arbetar på ett induktivt sätt med våra elever. Med det här menar han att vi
bör låta eleverna själva komma fram till och upptäcka samband och skillnader inom
matematikens värld. I en av intervjuerna får den aktuella eleven på egen hand hitta
sambandet. Eleven i fråga kan inte ”se” uppgiften, på så sätt att han är osäker på om uppgiften
kräver area- eller omkretsberäkning. Med hjälp av konkret material, i det här fallet ett snöre,
löser han uppgiften och korrigerar felet han gjort innan.
Att elever inte kan skilja på just area och omkrets kan bero på flera saker. Unenge(1998)
menar att begreppen ofta behandlas parallellt, vilket vi också ser i det aktuella läromedlet,
Matteborgen. Boken är uppbyggd på så sätt att omkretsuppgifter alltid följs av areauppgifter.
När vi i vår diagnos konkret efterfrågar antingen area eller omkrets klarar de flesta eleverna
att lösa uppgifterna. När vi sedan ställer en mer abstrakt fråga i intervjun ser vi tydligt att
förväxling sker. Elev 2 menar i intervjun att när man ska måla en dörr behöver man bara mäta
runt dörren för att veta hur mycket färg som behövs. När det gäller areaberäkning har vi också
sett att eleverna har stora svårigheter när det gäller enhetsformulering. Anderberg (1992) talar
28
om detta då han menar att eleverna har svårt att förstå vad som händer med enheten när vi
multiplicerar basen och höjden. Det ser vi tydligt vid ett intervjutillfälle, då elev 3 ombeds att
förklara vad som händer med enheten vid areaberäkning. Eleven vet att enheten förändras och
han kan sätta ut rätt enhet vid areaberäkningar, men inte uttrycka varför eller resonera där om.
Enligt Lpo94 kan vi dela upp kunskap i komponenter, vilket här innebär att eleven saknar
förståelse och förtrogenhet.
I: Jaha. Kan du räkna ut figurens area?
E3: Okej. 32 blir det.
I: Jaa / 32 vad för något?
E3: 32 // centimetertvå.
I: Nja / heter det centimetertvå?
E3: Nä / Jag vet att det heter nåt annat men det är i alla fall en tvåa efter där.
Eleven visar här tydligt att enhetsförändringen ställer till problem och att det är svårt att
förklara vad som skett och varför. Anderberg (1992) jämför detta med vad som i så fall sker
vid multiplikation av kronor, och hur eleverna uppfattar det.
Vad gäller beräkning av area och omkrets ser vi utifrån diagnosresultatet att eleverna klarar
de grundläggande uppgifterna. Det tyder på att eleverna egentligen har relativt god kunskap
kring area och omkrets. Öberg (1998) menar dock att skolan misslyckas i att knyta an till den
kunskap eleverna redan har med sig. Han anser att skolan på så sätt kringgår elevernas
tidigare erfarenheter. I och med detta är det viktigt att läraren introducerar och tillhandahåller
många lämpliga och givande exempel (Skemp, 1987). Det ger eleverna möjlighet att tillämpa
och bygga vidare på de begrepp man arbetar med.
29
7. Diskussion
Efter genomförande av diagnos och intervjuer upplever vi att det finns flera faktorer som
ligger till grund för elevernas missuppfattningar kring area och omkrets. Det vi tror är den
största anledningen till att det ser ut så här är att eleverna inte fått tillräckligt med tid och
material för att befästa sina kunskaper.
Uppgift 8 i vår diagnos är, som tidigare nämnt, kopierad från NCM:s Kängurutävling, avsedd
för skolår 3-4. Då tävlingen ägde rum 2006 blev svarsfrekvensen endast 20 %. Vid
genomförande av vår diagnos ger samma uppgift 40 % rätta svar. Detta anser vi är mycket
lågt, då eleverna är minst två år äldre än eleverna uppgiften är avsedd för. Frågan är då om
uppgiften är för svår, eller om eleverna brister i kunskapsnivå? Kängurutävlingen är utformad
med kursplanen och läroplanen som utgångspunkt och bör därför vara väl anpassad för den
kunskap eleverna bör besitta. Uppgiftsmakarna har dessutom god insikt i vad elever bör
kunna i dessa åldrar. Därför anser vi att detta är ett tydligt exempel på att våra elever brister i
geometrikunskaperna. En fråga vi ställer oss är om vi använt samma uppgift med elever som
ännu inte introducerats för areaberäkning, hade vi då fått ett annorlunda resultat? De elever vi
nu undersökt kan tänkas förväxla area och omkrets, och på så sätt blir de osäkra på vad
uppgiften frågar efter. Med yngre elever som endast arbetat med begreppet omkrets, finns
kanske inte något alternativ för hur uppgiften ska hanteras. Det skulle vara intressant att
undersöka hur ett sådant scenario skulle se ut.
7.1 Lärandesituationen
En annan viktig omständighet i sammanhanget är pedagogen. En lärare som väljer att ägna
mycket tid åt att arbeta med olika slags uppgifter kring area och omkrets ger möjlighet för
eleverna att tillägna sig djupare kunskap kring begreppen. Vi menar också att man som lärare
bör låta sina elever arbeta med så kallade rika problem. Detta innebär flerstegsräknande, där
en enda uträkning inte ger svar på uppgiften. Det kräver också ett lite annorlunda tänkande,
kring de begrepp som är aktuella. Rika problem har ofta en verklighetsanknytning, något som
vi tror är väsentligt för att eleverna ska förstå nyttan av matematiken. Vi ser tydligt i våra
intervjuer att eleverna ofta har svårt att förklara vad för vardaglig nytta man kan ha av area
och omkretsberäkningar. Detta upplever vi som väldigt konstigt, eftersom detta område är ett
av de mest vardagsbaserade inom matematiken. Att knyta begreppen till vardagssituationer
30
ger eleverna förutsättningar för att bättre minnas och befästa sina kunskaper, något som
bevisligen leder till att elevernas kunskaper består. Rika problem kommer också till sin
optimala fördel när eleverna får arbeta med uppgifterna i grupp. Flera av våra källor menar,
precis som vi vill poängtera, att eleverna ska få möjlighet att diskutera, reflektera och
upptäcka matematiken tillsammans. Under våra VFU-perioder har vi flera gånger sett hur
elever utvecklas och stärker sina kunskaper när de får experimentera och laborera fram
lösningar på problem
Ibland har vi märkt att pedagoger anser att det är ”fult” att låta eleverna använda konkret
material inom matematiken, och att det också ses som sämre i sammanhanget. Ofta är
läromedlet det enda som figurerar inom matematikundervisningen och det här tror vi har en
hämmande effekt på våra elever. Konkret material och vardagsbaserade rika problem borde
utgöra en naturlig del av matematikundervisningen, så även i de senare skolåren. Detta ger
eleverna förutsättningar för att förbättra sitt matematiska kunnande.
I läromedlet Matteborgen förekommer omkrets och area oftast i samma kapitel. Vi tror att
detta leder till förväxling och missuppfattningar. Vi tror att ett bättre alternativ är att arbeta
med begreppet omkrets på flera olika sätt. Då bör man arbeta, inte bara med de vanliga,
regelbundna figurerna, utan även med konkret material och oregelbundna figurer ”utan
vinklar”. Det samma gäller sedan när areabegreppet introduceras. Vi har under
undersökningens gång funderat på varför många läromedel väljer att behandla area och
omkrets tillsammans, då det endast verkar leda till att eleverna förväxlar begreppen. Vi är
medvetna om att begreppen kompletterar varandra, och att man genom beräkningar kan räkna
ut den ena med hjälp av den andra. Trots detta tycker vi att omkrets ska introduceras först,
och befästas ordentligt, innan areabegreppet behandlas. I läromedlet saknar vi öppna
uppgifter och de uppgifter som är lite mer kluriga har en hjälpande ”drake” i marginalen som
leder in eleverna på rätt spår.
Vi ser tydligt att det mekaniska räknandet fungerar bra. Detta är enligt vår mening beroende
på att läromedlen ser ut så. I Matteborgen finns få uppgifter där eleverna själva ska lista ut
vad som egentligen efterfrågas (ex. area eller omkrets). De flesta uppgifterna innebär att
eleverna ska beräkna area eller omkrets på regelbundna figurer med kända sträckor. Efter att
ha granskat Matteborgen, från bok 4A till 6:ans fördjupningsbok, upplever vi att det finns
alldeles för få uppgifter som behandlar området. Att tro att våra elever efter ca tio omkrets31
eller areauppgifter får möjlighet att befästa sin kunskap anser vi är fel. Vi upplever att
uppgifterna i Matteborgen ofta är konstruerade i ”rutnätsform”, d.v.s. figurerna är ritade
ovanpå ett rutsystem. Vi tror att detta ibland leder till att eleverna drar slutsatsen att rutnät
betyder areaberäkning. I och med detta anser vi också att om uppgift 7 i vår diagnos haft rutat
underlag skulle lösningsfrekvensen ha varit högre.
Vad gäller uppnåendemålen i kursplanen för matematik tolkar vi det som att våra diagnoser
visar att eleverna faktiskt når målen som rör area och omkrets. Vi menar däremot att målen
känns lågt ställda inom just detta område. Vi tycker att eleverna borde sträva efter att fördjupa
sitt kunnande och på detta sätt få en bredare och mer bestående kunskap. Vi som blivande
matematiklärare har under en lång tid fördjupat oss i ämnet och har kanske på så sätt för höga
förväntningar på eleverna. Är det så att vi egentligen borde nöja oss med att eleverna bara kan
beräkna figurers omkrets och area? Är det så som en av eleverna ger uttryck för, att vi lurar
våra elever när vi ”krånglar till” uppgifterna, eller är det ett viktigt steg i elevernas framtida
matematikutveckling? Vi anser att så är fallet. Det är viktigt att eleverna kan använda de
kunskaper de faktiskt har, men också att de kan förstå varför och därefter bygga vidare, då
t.ex. inför högre studier.
7.2 Språket
En annan faktor som påverkar både elevernas kunskaper och vår undersökning är språket.
Som vi tidigare nämnt är det matematiska språket redan i skolår fem ganska avancerat.
Läroboken introducerar begrepp som anses vara självklara, men som för många elever leder
till problem. Vi tror också att läroboken formulerar frågor på ett visst sätt, som eleverna
vänjer sig vid och finner strategier för att lösa. Detta kan vara en anledning till att vår diagnos
fick det resultat som den faktiskt fick. Då vi formulerar oss på ett visst sätt, kan detta ställa till
det för eleven. Vid ett av intervjutillfällena framkommer att eleven inte riktigt förstått
frågeformuleringen. Med hjälp av intervjuaren löser eleven uppgiften på ett tillfredsställande
sätt. Ett exempel på det här är om vi tittar på diagnosfråga 9. Vad vi funderar över i
sammanhanget är om vi hade fått ett annat resultat om vi utryckt oss annorlunda. Frågan som
nu ställs avser vilket område som är störst. Om vi istället frågat vilket område som har störst
area, kanske vi fått ett annorlunda resultat. Vi tror att samtliga elever hade förstått frågan
bättre och därmed också svarat rätt. Detta påstående bygger vi på att flertalet elever vid
32
intervjuerna visar god uppskattningsförmåga kring areabegreppet, då de vet att vi frågar efter
just area.
Något som vi tror har påverkat vårt resultat är det faktum att vi inte känner eleverna så väl.
Detta kan leda till att eleverna svarar något som de tror att vi vill höra, eller att de helt enkelt
inte känner sig bekväma i intervjusituationen. När vi genomförde intervjuerna hade vi vetskap
om detta och förhöll oss till det så som att resultatet ändå är tillförlitligt. Något som också
påverkat vårt resultat är vår konstruktion av diagnos och intervjuer. Vi måste här ställa oss
frågan om vi verkligen fått svar på det vi ville mäta i vår undersökning. Som tidigare nämnt
har våra formuleringar möjligen påverkat det resultat diagnosen gett. I de fall diagnosen följts
av en intervju känner vi att valideringen av vårt resultat är tillförlitlig. Där gavs eleverna
chansen att själva utveckla och förklara sina tankar.
7.3 Avslutande reflektioner
Något som skulle kunna vara intressant att arbeta vidare med är att utföra samma
undersökning, men med ett större elevantal som underlag. Detta för att ytterligare kunna
avgöra om resultatet i vårt arbete är tillförlitligt, då vår undersökning endast avser ett mycket
begränsat underlag. Intressant skulle också kunna vara att se samma undersökning i andra
delar av landet, eller kanske också i andra länder. Kan resultatet variera geografiskt? Ett annat
scenario som kan vara givande att titta närmare på är att återkomma till samma elever i slutet
av skolår 9. Att då granska elevernas kunskap igen kring begreppen och huruvida de har
utvecklat sin förståelse inom området kan ge spännande resultat. Dessutom skulle det, som vi
tidigare nämnt, vara spännande att göra vissa av uppgifterna med yngre elever, som ännu inte
introducerats för areabegreppet. Detta för att undersöka hur lösningsalternativen då skulle se
ut.
Hur kan vi som framtida pedagoger se till att våra elever befäster och fördjupar sin kunskap
kring area och omkrets? Som tidigare nämnt anser vi att man bör arbeta med ett
begreppsområde i taget. Eleverna bör dessutom arbeta med olika slags uppgifter, där de får
möjlighet att lösa problem och inte bara mekanisk räkning i läroboken. I vårt datoriserade
samhälle utförs mycket av den mekaniska räkningen av datorer eller miniräknare. Om detta är
bra eller dåligt låter vi vara osagt men eleverna måste enligt vår mening ha kunskap kring
bägge delar. Att arbeta med konkret material är ännu ett sätt för att underlätta elevernas
33
inlärningsprocess. På det här sättet får de chans att inte bara lösa uppgifter, utan också
handgripligen uppleva uppgiften. Uppgifterna bör vara verklighetsbaserade så att eleverna får
möjlighet att se vikten av att lära sig beräkningarna, och ett syfte med sin kunskap.
34
8. Källförteckning
Anderberg, B. (1992) Begrepp och termer i geometri. (Red) Emanuelsson, G Johansson, B &
Rydling, R. Geometri och statistik. Lund: Studentlitteratur
Bryman, A. (2004). Samhällsvetenskapliga metoder. Korotan Ljubljana : Liber.
Eriksson, K, H (2001) Om barns förmåga att bilda begrepp. (Red.) Emanuelsson, G, m.fl.
Matematik – ett kommunikationsämne. Kungälv: Grafikerna Livréna
Jacobsen, D, I (2002) Vad, hur och varför. Lund: Studentlitteratur
Kilborn, W & Löwing, M. (2002) Baskunskaper i matematik. Sverige: Studentlitteratur
Skemp, Richard R. (1987). The psychology of learning mathematics. Hillsdale, New Jersey:
Lawrence erlingbaum association publishers
Skolverket (2006) Läroplanen för det obligatoriska skolväsendet, förskoleklassen och
fritidshemmet. Stockholm: Fritzes
Skolverket (2007) Andelen behöriga till gymnasieskolan är den lägsta på tio år.
(20.11.2007). http://www.skolverket.se/sb/d/1716/a/9642
Unenge, J. (1994). Lära matematik. Lund: Studentlitteratur
Unenge, J. (1988). Matematikdidaktik för grundskolan. Lund: Studentlitteratur
Öberg, U. (1998). Elevers uppfattning av area. (Red.) Gran, B. Matematik på elevens
villkor. Lund: Studentlitteratur.
35
Bilaga 1 Diagnos
Namn: _____________________________
1. Kan du rita en figur och visa hur du räknar ut omkretsen?.
2. Kan du rita en figur och visa hur du räknar ut arean?
3. Rita två olika rektanglar med omkretsen 18 cm.
4. Rita två olika rektanglar med arean 18 cm2
5. Vad ska stå efter talet på raden? Välj bland enheterna.
e) Ett sovrums area kan vara 17 _____
cm2
f) En tavlas omkrets kan vara 300 _____
m2 cm
g) Arean av en dörrmatta är ungefär 24 _____
h) Översidan på en tändsticksask är ungefär 19 _____
mm2
dm2
m
dm
6. Går det att göra två figurer som har samma omkrets men olika area? I sådana fall visa
hur. Ledtråd: tänk dig att du har ett 20 cm lång snöre och knyter ihop ändarna, kan du
då göra olika figurer? Har dessa figurer lika stor area?
7. Beräkna figurens omkrets och area.
36
8.
9. Vilket område är störst?
10. Kan du genom att rita i figuren och skriva berätta hur du skulle bära dig åt för att
räkna ut arean på denna figur?
11. Beräkna arean på triangeln:
37
38
Bilaga 2 Intervjuer
Flicka 12 år
I = intervjuare
E= elev
I: Då tänkte jag fråga dig lite om diagnosen du har gjort.
E: Mm //
I: Här har du ritat en rektangel och räknat ut omkretsen. Hur tänkte du då?
E: Jag tog och mätte varje sida, och sen plussade jag liksom ihop. 26 / Alltså blev det
tillsammans.
I: Mmm / 26?
E: Ja, asså centimeter. Tror jag // eller ja, det är det.
I: Kan man räkna ut arean på den här (pekar på rektangeln)?
E: Ja. 8 gånger 5 är 40. Så 40 är arean.
I: 40 vadå?
E: ehh // kvadrat // ehh / kvadratcentimeter. Ja.
I: Ja, just det. Här har du ritat två olika rektanglar. Har de något gemensamt?
E: Gemensamt?
I: Ja, är det något som är likt mellan rektanglarna?
E: Jaha, ja, man skulle ju ta två rektanglar, med samma omkrets. 18.
I: Ja. Hur tänkte du när du löste det här?
E: Jag tänkte hur får jag 18 på olika sätt? Alltså så att allt tillsammans blir 18. Och då blev det
bara 4 plus 4 är 8, och så är det 10 kvar. Asså 5 på varje sida (pekar samtidigt på ”sin”
rektangel). Sen kunde jag komma på att 3 plus 3 är 6, och så blir det 12 kvar. 6 på varje sida.
I: Jättebra. Vad var nästa uppgift?
E: Ehh, vänta (letar bland pappren, och läser sedan högt); Rita två olika rektanglar med arean
18 cm2. Ja, asså den här fattar jag inte.
I: Kan du berätta hur du börjar tänka, så kanske vi kan lösa den ihop?
E: Okej. Jag tror det är nåt med omkretsen här också / men vänta / jo men jag fattar. Om den
här sidan (pekar på tidigare ritad rektangel) är 2 centimeter och den här andra är 9, då blir ju
arean 18.
I: Ja, det blir den ju faktiskt. Du kan ju rita en sån här (pekar på pappret) så visar du ju ändå
att du kan den!
E: Okej. (ritar)
39
I: Kan vi göra en till, som inte ser likadan ut?
E: Eeehh, typ 7, nä / 6 / nä / nä, det går inte.
I: Det går inte?
E: Nä, det går inte jämnt upp.
I: Okej. Vi kan gå vidare så länge. Vi kan ju titta på uppgift 6.
E: Okej. (läser den tyst). Ja, den här går ju inte heller.
I: Kan du försöka förklara hur du kommer fram till att den inte går?
E: (suckar) Mm, här kanske man har en bit (syftar på sida, int.anm.) som är typ / ehh / 4. Då
måste andra sidan vara 5 ju.
I: Okej.
E: Ja, och då blir ju arean 20.
I: Jaha. Men hur var frågan?
E: Ja, att göra 20 i area.
I: Läs en gång till.
E: (läser tyst igen) Jaha! Men det blir ju ändå samma.
I: Okej. Och det går inte att göra den på något annat sätt?
E: Nää, det tror ja inte.
I: Om den ena sidan är 2 centimeter då?
E: Ehh (räknar på fingrarna) / nä, då blir ju den andra sidan 8.
I: Rita den!
E: Okej. (ritar upp rektangel med sidorna 2 och 8)
I: Mm. Vad har den här för area?
E: Hmm // Vänta / 16.
I: 16 vadå?
E: Centimeter. Eller kvadratcentimeter menade jag.
I: Då fick vi ju en annan area nu!
E: Mm. Ja, just det, då går ju det.
I: Vad är area för något?
E: Det är väl detta (pekar innanför rektangelns sidor)
I: Kan man förklara det på något sätt?
E: Ehh, det är / det som får plats innanför strecken.
I: Ja, det kan man säga. När kan man ha nytta av att kunna räkna ut area?
E: (funderar) I boken brukar det handla om att man ska mäta en bit jord eller så. Annars vet
jag inte redigt.
40
I: En bit jord?
E: Jamen typ / en jordbit för grisar att gå på eller nåt.
I: Okej. Om det här skulle vara en jordbit för grisarna (pekar på uppgift 10 i diagnosen), kan
vi räkna ut arean då?
E: Nä / eller jo, det går väl. Eller kanske.
I: Hur tror du att man kan göra då?
E: Hm // Man kan väl ta ett snöre runt om och sen lägga det rakt liksom.
I: Hur menar du då?
E: Jamen om man tar ett snöre runt om här och lägger precis på, så kan man ju lägga ut det
fint sen. Asså rakt.
I: Ska vi prova?
E: Ja, kan vi väl. (I hämtar garn i annat rum)
I: Sådär, kan du mäta hur lång bit vi behöver?
E: Mm. (lägger ut garnbiten noggrant ovanpå pappret, klipper sedan av en bit.)
I: Jaha. Hur gör vi nu då?
E: Lägger den rakt så här. Som en fyrkant liksom. (lägger snöret som en rektangel) Så vi kan
räkna ut.
I: Har den samma area om jag gör så här? (drar ihop snöret till en rektangel med liten höjd,
bred bas)
E: Ehh // (skrattar) Nä, tror inte de.
I: Eller så här? (lägger tråden ungefär som i uppgift 10)
E: Nä. Det går inte att räkna ut då. Det blir ju inte jämnt upp.
I: Okej. Kan du räkna ut arean på triangeln här?
E: Ja. 4 gånger 3 delat med 2 / 6.
I: 6?
E: Ja. Det blir det.
I: Varför delade du med två?
E: Därför att man ska det när det är en triangel.
I: Jaha. Vet du varför man ska dela med 2 då?
E: // nä, det vet jag väl inte.
41
Pojke 12 år.
I: Då ska vi se. Här är diagnosen du gjorde häromdagen.
E: Mm.
I: Kan du berätta för mig hur du tänker på uppgift 1?
E: Aaa. Jag ritade en fyrkant här (pekar) och mätte.
I: Vad mätte du?
E: Sidorna. Och så plussade jag dom.
I: Mm. Hur gjorde du på uppgift 2 då?
E: Jag tog samma, men jag tog gånger istället.
I: Okej.
E: Så här blev det 10, och sen 6.
I: Ja just det! Då har du ju räknat ut både area och omkrets.
E: Mm.
I: Du kan väl berätta hur du tänkte på uppgift 3?
E: Jag tänkte att det inte går. Det är ju alltid 18.
I: Hur menar du då?
E: Ja, att 18 är ju alltid 18.
I: Okej. Hur tänker du då?
E: Ja, den kommer ju alltid vara lika lång, även om jag ändrar formen liksom.
I: Ja, det är sant. Men om du får ändra den, finns det olika sätt att göra den då?
E: Ehh / jag vet inte.
I: Jag har ett snöre här som är 18 centimeter långt. Kan du göra olika rektanglar av det?
E: Ehh / Kanske. (lägger snöret på olika sätt och gör flera olika rektanglar). Nä. Alla blir
samma.
I: Samma på vilket sätt?
E: Snöret är ju ändå lika långt.
I: Ja, men de ser inte likadana ut, rektanglarna som du gjorde?
E: Nä.
I: Men då har du just gjort olika rektanglar men med samma omkrets, alltså 18 cm. Snöret är,
precis som du sa, alltid lika långt, men inuti här (pekar på ytan innanför snöret) är det olika.
E: Jaha! Då fattar jag kanske /
I: Bra! Vi kan gå vidare. På uppgift 4 skulle du försöka rita olika rektanglar som har samma
area.
E: Ja, det går i alla fall inte (skrattar).
42
I: Inte?
E: Nä. Arean är ju aldrig samma. På olika figurer liksom.
I: Okej. Hur räknar vi ut area?
E: Ja, sidan där (pekar på basen) gånger den här (pekar på höjden).
I: Ja, just det! Bra! Ska vi prova att göra en som har arean 18 kvadratcentimeter?
E: Okej. Ehh, nåt gånger nåt ska bli 18 eller? / 2 gånger 9!
I: Ja! Just det!
E: Men det är väl den enda / ja, det finns inte i nån annan tabell / eller (mumlar) jo. 6 gånger
3 blir 18!
I: Ja. Jättebra! Så en rektangel med sidorna 6 centimeter och 3 centimeter skulle ju gå bra! Du
kan ju rita dem här så ser vi ju hur du fixade det!
E: Okej. (ritar rektanglarna) Så!
I: Så! När kan man ha nytta av att kunna räkna area?
E: Ehh, det vet jag inte.
I: Kan du komma på något?
E: // nä
I: När man ska måla en vägg kanske? Så att man vet hur mycket färg som kommer att gå åt?
E: Jamen då mäter man ju bara rakt om.
I: Hur då?
E: Ja, hur långt det är runt om dörren. Så vet man ju.
I: Men vad är det vi mäter om vi mäter runt om dörren? Vi kan väl rita en dörr här på pappret.
E: Mm. (ritar en rektangel)
I: Om vi mäter den här runt om, vad är det vi får fram då?
E: Ja / hur mycket färg vi behöver för att måla den.
I: Och vad är det du har mätt?
E: / hur lång dörren är.
I: På uppgift 8 i diagnosen vill jag att du förklarar för mig hur man gör när man löser den.
E: Jaa / Man räknar hur många rutor som får plats innanför snöret och sen räknade jag vilken
av dom andra som har lika många rutor.
I: Okej. Ska vi prova med det här snöret? (lämnar över snöre som är utmätt för att passa)
E: Visst. (börjar att passa ovanpå pappret) Det går ju inte / eller, här kanske / Ja, den här är
det ju. Inte C. Men hur kan det bli så?
I: Ja, hur kan det bli så?
43
E: Man kan tro att det skulle bli (ohörbart) för det är samma rutor. Men snöret går ju att
spänna ut (spänner ut så långt det går). Man kan aldrig tro på area och sånt, det är alltid något
lurt. I boken är det jämt fyrkanter o så, det fattar jag, men inte varför det ska vara sånt här!
I: Men man kan ju räkna ut area på trianglar och cirklar också. Och till och med på den här
(pekar på uppgift 9 i diagnosen).
E: ja, på ett ungefär ja. Det går ju inte jämnt upp om man tar den. Man får ju ta en liten
fyrkant över, så nära som det går. (pekar ut en fyrkant som passar ”så bra som är möjligt”)
I: Kan du räkna ut arean på den här? (pekar på uppgift 9)
E: Ja, det är ju bara sidan gånger den där sidan.
I: Så det spelar ingen roll om sidorna är raka?
E: Näpp. Det går ju att mäta ändå.
I: Hur gör man med trianglar då?
E: Som vanligt.
I: Kan du visa mig på uppgift 11?
E: Ja. Det är ju bara å ta 4 gånger 3 är 12. 12centimetertvå.
I: Centimetertvå? Varför heter det centimetertvå tror du?
E: Därför att man har gångrat två olika centimetersiffror.
(Jämför med rektangel och eleven ser då att det inte stämmer, och att man måste dividera med
två. Kan dock inte förklara varför)
44
Pojke 12 år
I: Jag tänkte att vi ska titta lite på din diagnos. Du kan väl förklara lite för mig hur du har
tänkt?
E: Mm.
I: Hur tar du reda på omkretsen av den här rektangeln (visar en rektangel på rutat papper)?
E: Jag mäter runt om och plussar alla sidorna. Ska jag göra det här?
I: Ja, gärna!
E: (mumlar) 4 / 4 / 23, nej 24! 24 är det.
I: 24 vadå?
E: Ja, centimeter.
I: Jättebra! Vad är area för något då?
E: Ehh, typ / asså det som är inuti där (pekar på ytan innanför rektangelns sidor)
I: Hur kan man räkna ut det?
E: Man tar / ehh / den här gånger den. (pekar på basen och höjden)
I: Jaha. Kan du räkna ut figurens area?
E: Okej. 32 blir det.
I: Jaa / 32 vad för något?
E: 32 // centimetertvå.
I: Nja / heter det centimetertvå?
E: Nä / Jag vet att det heter nåt annat men det är i alla fall en tvåa efter där.
I: Ja, just det. Det heter ju kvadratcentimeter, känner du igen det?
E: Mm, ja, just det.
I: Så 32 cm2 är arean här?
E: Mm.
I: Varför tror du att det heter kvadratcentimeter?
E: För att visa att vi har tagit gånger.
I: Vi kan ta och titta på en uppgift som du har löst på diagnosen häromdagen.
E: Okej.
I: Uppgift 7 till exempel; hur gjorde du för att räkna ut den?
E: Ehh / jag började med att räkna ut omkretsen, och då la jag ihop alla siffror. 10 blir det då.
Sen tog jag bara 2 gånger 4, och det blir 8. Så 8.
I: Okej. Om vi gör en rektangel som ser ut så här då? (ritar på diagnospappret så att
rektangeln alla vinklar blir räta) Hur stor area har den här?
45
E: Ja / det blir väl samma. Eller nä / eller jo / då kan jag ju ta 2 gånger 4 och det blir / 8. Ja,
det blir samma faktiskt.
I: Men kan de ha samma area, nu och innan?
E: / vet inte
I: Du visade mig innan vad som är rektangelns area. Vad var det nu igen?
E: Ja, det som är innanför här / men då kan ju inte båda två ha samma. Det borde ju bli mer
nu. Men jag fattar inte hur man ska göra då.
I: Kan du komma på vad vi har ändrat nu?
E: / ja, alltså du gör ju den större när du drar det där strecket. Så det måste ju vara nåt annat.
Man kanske ska ta 3gånger 2 på den första, och sen 4 gånger 2 när den liksom är hel? (kikar
frågande på intervjuaren)
I: Om du tar 3 gånger 2, vad händer här borta då? (pekar längst till höger på figuren i
uppgiften)
E: Ehh / Ja, det kommer liksom inte med.
I: Nä, det gör inte det. Hur kan vi då göra?
E: Strunta i den biten! (ler, och fortsätter sedan) Nä, det måste finnas ett sätt för den lilla
också.
I: Ja / skulle vi kunna dela upp den på något sätt?
E: Ja! Vi drar ett streck här och sen räknar. (mumlar) 3 gånger 2 / 6. 1 gånger 1 / är ju 1. Ehh /
den ena får ju 6 och den andra får 1. Kan man bara plussa på dom då?
I: Ja, här kan man faktiskt det. Vad får den här figuren för area nu då?
E: Ja, 7 / cm2!
I: Jättebra jobbat! Hur tänkte du på uppgift 8 då?
E: Ja, jag räknade rutorna däri, och så la jag ut dom på en ny fyrkant.
I: Jag har ett snöre här som är lika långt, kan du passa in det och se om det är C som är rätt?
E: Okej / (mäter) Nä / men / varför blir det den??
I: Ja, hur kan det bli det?
E: Vet inte
I: Vad är det du har räknat när du räknat rutorna här inuti?
E: / Ehh, jag vet inte / omkretsen / ?
I: Omkretsen vad är det?
E: Hur långt det är / jaha! Jag har ju kollat hur mycket som får plats inuti! Men blir inte det
samma?
I: Mät så får vi se. Vilken av dom är rätt då?
46
E: Ja, det är ju den. Men då ändras bara det inuti, och inte det runt om. Snöret är ju lika långt
ändå.
I: Ja, just det! Bra! Kan du visa hur du fick svaret på uppgift 10 också?
E: Okej. Jag ritade en fyrkant så nära jag kan, och sen räknade jag bara arean på den. Så får
man ju skriva ett sånt där likamed-tecken som inte är liksom precis på pricken. Då fattar ju
Therese (läraren) att man visar att det är ungefär.
47
Bilaga 3 Brev till föräldrarna
Hej föräldrar!
Vi är två studenter som studerar på Lärarutbildningen vid Växjö universitet. Vecka 39-43 är
vi ute på vår praktik. Under dessa veckor kommer vi att diagnostisera och intervjua eleverna i
klassen angående deras kunskaper kring begreppen area och omkrets.
Diagnosen vi gör kommer att ligga till grund för valet inför intervjuerna. Dessa kommer att
ske på skolan och givetvis kommer inga namn på barnen att nämnas i vår redovisning av
resultaten eller i något annat sammanhang. Resultatet kommer således att behandlas
konfidentiellt.
De resultat vi får fram kommer att presenteras i vårt examensarbete. Detta kommer att finnas
tillgängligt på Internet på Växjö Universitets hemsida. Det kommer även att presenteras på
vår lärarutbildning inför våra kurskamrater samt lärare. Återigen vill vi påpeka att inga namn
på varken barn, lärare eller skolor kommer att nämnas.
Var vänlig och fyll i ert barns namn, kryssa i ett av alternativen och ta med lappen tillbaka till
skolan senast måndagen den 1:a oktober.
Vänliga hälsningar,
Malin Eriksson och Gustav Olsson
----------------------------------------------------------------Mitt barn heter __________________________________ och det går bra att intervjua
honom/henne i er undersökning.
Mitt barn heter _________________________________ och jag vill inte att han/hon
blir intervjuad av er.
48
Matematiska och systemtekniska institutionen
SE-351 95 Växjö
Tel. +46 (0)470 70 80 00, fax +46 (0)470 840 04
http://www.vxu.se/msi/
49
Växjö
universitet
Matematiska och systemtekniska institutionen
SE-351 95 Växjö
tel 0470-70 80 00, fax 0470-840 04
www.msi.vxu.se