Урок 5

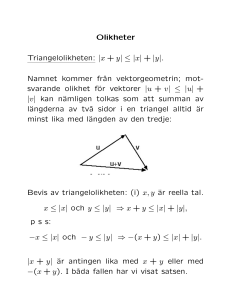
Lektion 11: Olikheter
Definition. a>b om a–b är ett positivt tal.
a≥b om a>b eller a=b.
1. Ringa om påståenden som är rätta och strycka de som är felaktiga.
a. 1000>999 b. 1000<999 c. 1000≥999
d. 1000≤999
e. –5>0
f. –5<0
g. –5≤0 h. 6 > –5 i. –6>5
–6<–5
2. Visa att
a) om a>b och b>c så är a>c
b) om a≥b och b≥c så är a≥c
c)* om a≥b och b≥c och a=c så är både a=b och b=c.
Definition. Ett påstående med olikhetstecken > ≥ < ≥ och med en eller flera
obekanta kallas en olikhet.
Exempel. x>4,
0<x≤5,
2x+3>x–2,
x+3y<z
Vi kommer att betrakta bara olikheter med en obekant, vanligtvis med x som
obekant.
Definition. Om man sätter in ett värde på den obekanta och får ett rätt påstående
så kallas detta ”värdet satisfierar olikheten” eller ”värdet är en lösning till
ekvationen”.
Exempel. Värdet x=5 satisfierar olikheten x>4 ty påståenden 5>4 är rätt. Däremot
x=1 ej satisfierar olikheten x>4 ty 1>4 är fel.
3. Ringa om x-värden som är lösningar till olikheten 3x≤15 och strycka de som ej är
lösningar:
a. 3 b. 0 c. 1000
d. –4 e. 2.5
f. 5
g. 11/2 h. 36/7
4. Ringa om olikheter som har en lösning x=7 och strycka de som har den inte:
a. x>5 b. x≤7 c. 3x>20
d. –x<1 e. 3x+20>5x
f. x2≤50
g. 0,1–1/x>0
5. Visa att
a) om a>b så är a+c>b+c och a–c>b–c
b) om a>b och k>0 så är ka>kb och a/k>b/k
c) om a>b och c>d så är a+c>b+d.
Anmärkning. Egenskapen 5a tillåter att flyttar termer mellan leden i olikheten utan att
tappa lösningar. Egenskapen 5b tillåter att multiplicera eller att dela båda led i en olikhet
med ett positivt tal utan att tappa lösningar. OBS! Multiplicera en olikhet med ett negativt
tal eller med ett uttryck kan vara farligt!
Detta räcker för att lösa linjära olikheter på samma sätt som man löser linjära ekvationer.
Definition. Att lösa en olikhet med en obekant betyder att skriva om den till formen x<5
eller x≥7,5 (d.v.s. en enkel obekant i en led och ett tal på andra leden).
7. Lös olikheterna
a. x–5>0 b. 2x–13≤7 c. 3x<7x
d. 3x+10≥6x–11
e*
x(x+2)>(2+x)2
8* 9 pennor kostar mer än 11 euro fast mindre än 12 euro. 13 likadana pennor kostar
mer än 15 euro fast mindre än 16 euro. Det finns ingen rabbat. Bestäm hur mycket
kostar en penna.
Den 11 oktober, Metapontum, åk 1 http://sasja.shap.homedns.org/Metapontum/2007/ht1