Att ge problemlösning större utrymme i gymnasieskolans
advertisement

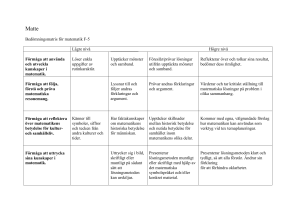
Elisabeth Samuelsson PDAX51 Att ge problemlösning större utrymme i gymnasieskolans matematikkurser Sammanfattning Problemlösning ses som en viktig del av matematikämnet både traditionellt och i kursplaner för matematik. Trots detta finns det tecken på att problemlösning inte får tillräckligt stort utrymme i gymnasieskolans matematikundervisning idag. Jag upplever åtminstone att det är sant när det gäller min egen undervisning. Därför vill jag koncentrera mig på hur problemlösning rent praktiskt kan tillämpas i undervisningen. För att undersöka detta vill jag använda mig av aktionsforskning. Jag kommer att planera problemlösningsaktiviteter med hjälp av den tidigare forskning som finns inom området som jag kommer att genomföra i min matematikundervisning. Aktiviteterna kommer att utvärderas både av mig och med hjälp av deltagande elever och kollegor. Under arbetets gång kommer jag att föra loggbok för att samla reflektioner och kunna följa arbetets utveckling. Bakgrund Problemlösning har sedan lång tid en central roll i matematikämnet, detta finns det mängder av exempel på. George Polya, framstående matematiker med stort intresse för undervisning, skrev redan 1945 ”How to Solve It”, en gedigen beskrivning av hur matematiska problem kan hanteras i undervisningen och vad detta kan leda till. Där beskriver han också hur Descartes hade påbörjat ett liknande projekt som aldrig avslutades eller blev publicerat. I Sverige har problemlösning varit en viktig del i läroplaner och kursplaner för matematik under de senaste decennierna. I gällande kursplaner för gymnasieskolan (Skolverket, 1994), handlar två av strävansmålen om problemlösning och det första uppnåendemålet för samtliga matematikkurser innehåller frasen ”Eleven skall kunna formulera, analysera och lösa matematiska problem… ” (exv. Kursplan för Matematik A). I grundskolans kursplan för matematik är ett av strävansmålen: ”Skolan skall i sin undervisning i matematik sträva efter att eleven… …– utvecklar sin förmåga att formulera, gestalta och lösa problem med hjälp av matematik, samt tolka, jämföra och värdera lösningarna i förhållande till den ursprungliga problemsituationen,…”(Kursplan för matematik) Under rubriken ”Ämnets karaktär och uppbyggnad” handlar nära hälften av texten om problemlösning. I skolverkets remissförslag till ämnesplan för matematik i den kommande gymnasiereformen skrivs under ”Ämnets syfte”: ”Det innefattar att utveckla förståelse av matematikens begrepp och metoder samt att utveckla olika strategier för att kunna lösa matematiska problem…” och ”Undervisningen ska stärka elevernas tilltro till sin förmåga att använda matematik i olika sammanhang samt ge utrymme åt problemlösning som både mål och medel.” samt som ett av målen att eleverna ska ges förutsättningar att utveckla: ”Förmåga att formulera, analysera och lösa matematiska problem samt att värdera valda strategier, metoder och resultat. ”( www.skolverket.se/sb/d/3398, 2011-01-04) Trots att problemlösning skrivits fram så tydligt i kursplanerna fann Boesen (2006) i sin jämförelse mellan nationella prov och lärarkonstruerade prov i matematik att problemlösningsuppgifter Elisabeth Samuelsson PDAX51 utgjorde en mindre del av de lärarkonstruerade proven än av de nationella proven. Detta kan tolkas som att problemlösning har en mindre framträdande roll i undervisningen i gymnasieskolan än vad som åsyftas i styrdokumenten. Även skolinspektionen (2010) fann i sin rapport under hösten att matematikundervisningen i majoriteten av de inspekterade gymnasieskolorna innehöll för lite problemlösning och för mycket algoritmräkning: ”Uppgifter av problemlösande karaktär som utmanar och stimulerar till diskussion är alltså vanligast på NV, men inte heller där förekommer det i någon större omfattning.” (s 18) Denna rapport bevisar inte att förhållandet är likadant i alla Sveriges gymnasieskolor men jag upplever att beskrivningen stämmer väl överens med min egen undervisning och det jag känner till om mina kollegors undervisning. Detta gör att jag upplever ett behov av utveckling min matematikundervisning. Då problemlösning är ett så väletablerat område inom matematikundervisning finns troligen omfattande forskning inom området. Trots detta verkar implementeringen i undervisningen vara liten. Därför vill jag koncentrera mig på det konkreta steget att införa mer av problemlösning i min undervisning. Litteratur Edman och Johansson (2009) har gjort en intervjustudie av några grundskollärares syn på problemlösning. Där identifierar de några olika uppfattningar om vad som menas med problem i matematikundervisning. Komponenter i uppfattningarna är att problem kan ha flera möjliga svar, att de kan vara utan specifika beräkningar och att problemlösning kan ses som en matematisk kompetens. De refererar också sju kriterier från Hagland m fl (Hagland m fl 2005 i edman och Johansson 2009 s 14-16) om vad som bör utmärka matematiska problem. Problem som uppfyller dessa kriterier kallas rika problem. Även Lindström (2009) har gjort en intervjustudie om matematiklärares uppfattningar om och användning av problemlösning i undervisningen. De fem lärare hon har intervjuat använder problemlösning på olika sätt och i skiftande omfattning och har olika syner på vad som kan uppnås genom arbetet. Lindström refererar även Ryve (Ryve 2006 i Lindström 2009 s 9) som menar att det saknas kurslitteratur om problemlösning för blivande matematiklärare i Sverige. Ett betydligt mer omfattande forskningsprojekt har genomförts av Wyndhamn, Riesbeck och Schoultz (2000). De redogör för att problemlösning ses som något positivt och varför det är så samt vad begreppet kan stå för med hjälp av ett postmodernt förhållningssätt. De väljer att dela in problemlösning efter två olika dimensioner, en som handlar om i vilken utsträckning problemlösningen tillämpar tidigare kunskap eller sker för att nå ny. Den andra dimensionen rör hur problemlösningen sker, om det är arbetssättet eller tankeprocessen som är det eftersträvansvärda. Med hjälp av dessa dimensioner ger författarna beskrivningar av fyra olika kategorier av problemlösning i undervisningssammanhang, A, B, C, och D enligt följande figur. Tillämpning Tillämpning B A Arbetssätt Tankeprocess C D Inlärning Inlärning De kopplar också sina kategorier till olika vetenskapliga eller pedagogiska synsätt som konstruktivism för kategori D eller kognitivism för kategori A. Dessutom ger författarna en modell Elisabeth Samuelsson PDAX51 för hur relationerna mellan lärare, elev och problem kan hänga samman med syftet för problemlösningen. Förutom sina resonemang kring vad som menas med problemlösning ger Wyndhamn, Riesbeck och Schoultz en bild av två olika ytterligheter eller poler som matematikundervisning kan variera mellan, en som utmärks av lärargenomgångar och tyst, enskild räkning och en som utmärks av matematiska samtal och problemlösning. Skolinspektionen (2010) menar att den förra är klart förhärskande i majoriteten av de skolor rapporten omfattar. Fokus i Boesens (2006) undersökning är inte framför allt problemlösning men i sin analys av provuppgifter väljer han att kategorisera dem efter vilka kompetenser de testar. Han påpekar i sin definition av problem att huruvida en uppgift är ett problem eller inte beror inte enbart på själva uppgiften utan även på den som ska lösa den och förkunskaperna hos den personen. För att en uppgift ska vara ett problem måste den innehålla något moment som skiljer den från välkända standarduppgifter för den som ska lösa uppgiften. Denna aspekt skulle placera Boesen i Wyndhamns m fl kategorier C eller D. Jag menar också att det är framför allt de kategorierna av problem som behöver större utrymme i undervisningen. Även citatet ovan från Skolinspektionen borde kunna tolkas som att det är den typen av problem de framför allt syftar på. Polyas redogörelse hamnar framför allt i kategorierna A och D då hans problemlösningsmanual behandlar problemlösning som en kompetens som eleverna kan tillägna sig med hjälp av hans metod. Kategori B skulle innebära problemlösning som ett arbetssätt för att befästa tidigare kunskaper. Detta skulle man möjligen kunna se som de problemlösningsuppgifter som ofta avslutar avsnitt i läromedel. Där är det givet vilket matematiskt innehåll som ska användas vid lösningen eftersom problemet hör till ett visst avsnitt och lösningen handlar ofta om att följa en metod som också är känd men där någon svårighet kanske dyker upp på vägen. Denna typ av problemlösning ser jag inget behov av att ge ytterligare utrymme i undervisningen och Wyndhamn m fl menar också att dagens läroplan knappast syftar på denna typ av problem. Syfte Syftet med arbetet är att undersöka hur jag kan ge problemlösning större utrymme i min matematikundervisning i gymnasieskolan. Delfrågeställningar som kan bli aktuella är: Varför har problemlösning så litet utrymme i undervisningen idag? Vilka effekter får det om problemlösning får ett större utrymme i undervisningen? Hur identifierar man problemuppgifter med lämplig nivå? Var kan man hitta problemuppgifter som är lämpliga för gymnasienivå? Hur kan man konstruera problemuppgifter som är lämpliga för gymnasienivå? Kan en problemlösningsmanual liknande Polyas utveckla elevers problemlösningsförmåga? Metod I min frågeställning förutsätter jag redan från start att inslag av problemlösning i matematikundervisning är något positivt. Detta är långt ifrån ett objektivistiskt förhållningssätt. Då problemlösning är en så central del av matematikämnet sedan så lång tid förutsätter jag att forskningen inom området är omfattande och jag vill fokusera på hur den kunskap som redan finns konkret kan implementeras i gymnasieskolan av idag. Trots att jag uppfattar problemlösning som något positivt ger jag inte särskilt stort utrymme åt det i klassrummet. Detta kan bero på mängder av omständigheter som styr mitt handlande. Styrdokumenten anger hur det svenska samhället menar att matematikundervisning på gymnasiet ska fungera. Trots detta är det möjligt att andra samhällsfaktorer påverkar min undervisning i annan riktning. Det skulle kunna handla om faktorer som hur elever fördelas mellan olika grupper, i vilken omfattning jag blir ersatt för mitt planeringsarbete eller vilket material som finns tillgängligt för mig att använda i undervisningen. Samtidigt har jag förmåga att reflektera över situationen och mitt handlande. Allt detta stämmer väl överens med hur människan och människans situation uppfattas inom kritisk teori enligt Alvesson och Sköldberg (2009). Som en gren från kritisk teori finns aktionsforskning som jag menar passar utmärkt för min forskningsfråga. Aktionsforskning har ofta ett syfte som ska leda till att stärka demokratiska förhållanden eller motverka något missförhållande som gör en viss grupp förfördelad. Riktigt så kommer det inte att fungera i denna studie men jag menar ändå att syftet kan kopplas till elevernas rättighet att få en så god undervisning som möjligt. Elisabeth Samuelsson PDAX51 Både Rönnerman (2004), Mills (2007) och McNiff (2002) illusterar aktionsforskning som cykliska processer. I enklaste form skulle den kunna se ut såhär: utvärdera reflektera agera McNiff påpekar dock att processen sällan följer en så behändig figur, dels liknar processen snarare en spiral eftersom ett varv i cirkeln inte leder tillbaka till utgångspunkten, dels är det troligt att delprocesser kommer att spinna iväg från huvudprocessen i egna minispiraler. I Rönnerman (2004) och Mills (2007) påpekas också att det mellan stegen i processen vid olika tillfällen behöver inhämtas kunskap om befintliga teorier, modeller eller ideér från andra källor. Jag föreställer mig att hinna med två mer omfattande cykler under arbetets gång. Arbetet kommer att sträcka sig från januari 2011 till januari 2012. Agerande-fasen måste med nödvändighet ska när verksamheten är igång. Under sommaren behöver därför de andra faserna ske. Detta utesluter inte att någon del av processen kan ha snabbare delcykler under arbetes gång. Arbetet kommer att starta med en reflektionsfas då jag inhämtar kunskap om problemlösning från litteratur och planerar för delaktiviteter som kan genomföras i de olika kurser som är igång under vårterminen. Under den fasen behöver jag också få tillåtelse av skolledningen för mitt arbete och informera berörda elever om vad jag tänker göra och vad jag vill uppnå. Därefter vidtar en agerandefas då jag genomför problemlösningsaktiviteter på olika sätt i undervisningen. Jag föreställer mig att aktiviteterna kan se ut på många olika sätt. Vara aktiviteter i helklass, mindre grupper eller individuellt, ske på lektionstid eller frivilligt utanför lektionstid, vara rena tankeövningar eller utnyttja konkret material och variera på fler liknande sätt. Innan terminsslut behöver jag också hinna med vissa valideringsaktiviteter som kan vara enkäter eller korta intervjuer med deltagande elever om hur de har uppfattat aktiviteterna eller att be någon kollega observera någon aktivitet och reflektera tillsammans med mig efteråt. Under sommarlovet blir det sedan dags för en utvärderingsfas och nästa reflektionsfas. När höstterminen startar är det dags för nästa agerandefas och sedan en sista utvärderingsfas innan arbetet ska avslutas. Efter att uppsatsarbetet är avslutat hoppas jag att det är möjligt att fortsätta arbetet på liknande sätt men i mindre omfattning. Under hela arbetets gång ska jag skriva loggbok över det jag läser och observerar och över mina reflektioner. Beroende på hur varje specifik aktivitet ser ut kommer det också att vara lämpligt att kanske ibland göra ljudinspelningar och någon annan gång kanske samla in skriftlig dokumentation. Jag ser ett tydligt dilemma med metoden. Då undersökningen sker i min egen verksamhet kommer de elever som deltar i aktiviteterna att stå i beroendeställning till mig. Trots detta är det viktigt att de deltar i aktiviteterna för att de själva vill och att de i utvärderingar är ärliga om hur de har upplevt aktiviteterna. För att underlätta detta vill jag försöka vara så tydlig som möjligt med vad som är arbetets syfte och att det är beroende av att de inte skönmålar det de upplever under aktiviteterna. Jag vill också i så hög utsträckning som möjligt låta eleverna delta när beslut ska fattas om vilka aktiviteter som ska genomföras och huruvida de själva ska delta. Den valda metoden kommer att medföra vissa svårigheter när det gäller valideringen. Undersökningen gäller min verksamhet och ingen annan har möjlighet att överblicka den så att det går att ta ställning till i hur hög utsträckning jag når mitt syfte. Validiteten blir beroende av att jag ger en ärlig beskrivning av hur processen har gått till och redogör för både positiva och negativa resultat på ett tydligt sätt. Det hade varit önskvärt att ha tillgång till någon eller några andra som kunde granska arbetet i sin helhet. Detta saknas det resurser till och jag blir beroende av om exempelvis någon kollega kan tänka sig att granska någon del av arbetet samt att samla på mig material under arbetets gång som kan stödja mina påståenden. När det gäller etiska ställningstaganden måste jag självklart få tillåtelse av skolledning och deltagare för att genomföra min undersökning. Det kan också bli aktuellt att be vårdnadshavare om tillåtelse i fall då eleverna är omyndiga och deltar på något specifikt sätt i någon aktivitet eller utvärdering av någon aktivitet. Ett svårare problem kommer konfidentialiteten att vara. När min undersökning ska rapporteras kan jag inte vara anonym, därmed kommer eleverna som grupp inte heller att kunna vara anonyma och ibland kommer det troligtvis att vara viktigt att ange i vilken kurs eller kanske på vilket program en viss aktivitet genomförs och därmed ringa in elevgrupperna Elisabeth Samuelsson PDAX51 ganska tydligt. För att inte hänga ut enskilda elever behöver jag undvika att kommentera enskilda elevers åsikter och agerande och hellre sammanfatta observationer för en hel grupp. Om det finns anledning att använda något från en specifik individ måste jag vara tydligt med att de skulle kunna bli identifierade och be om tillåtelse för det. Relevans De resultat jag kommer att nå kommer att vara starkt kopplade till den speciella situation där de har visats. Trots detta menar jag att undersökningen kan ha stor relevans för matematikundervisning i gymnasieskolan eftersom bland andra skolinspektionen pekar på att problemlösning är eftersatt i majoriteten av undervisningen. Om jag då kan indentifiera orsaker till varför det är så trots de tydliga skrivningarna i styrdokumenten och hitta sätt att ändra på det i min undervisning borde det kunna inspirera till liknande lösningar för andra eller om jag misslyckas till tankar om hur man kan göra istället. Tidsplan Februari-mars Litteraturstudier, samtal med skolledning för att få tillstånd April Utformande av några lektionsplaneringar Maj Genomförande av lektionsplaneringar Juni-juli Reflektion och analys av genomförda lektioner, ytterligare litteraturstudier Augusti Utformande av ytterligare aktiviteter Sept-Okt Genomförande av ytterligare aktiviteter, även med ytterligare kollegor? Nov-Dec Reflektion och analys, utformning av slutrapport Elisabeth Samuelsson PDAX51 Referenser Alvesson, M. och Sköldberg, K. Tolkning och reflektion. Vetenskapsfilosofi och kvalitativ metod. Lund: Studentlitteratur. Boesen, Jesper. (2006) Assessing Mathematical Creativity. Comparing national and teacher-made tests, explaining differences and examining impact. Doctoral thesis no.34, 2006. Department of Mathematics and Mathematical Statistics. Umeå: Umeå universitet. McNiff, J. with Whitehead, J. (2002). Action Research. Principles and Practice. London: Routledge Farmer. McNiff, J., Whitehead, J. (2005). Action Research for Teachers. A practical guide. London: David Fulton Publishers. Mills, G. (2007). Action Research. A Guide for the Teacher Researcher. Upper Saddle River: Pearson Education, Inc. Polya, G. (1988). How to Solve It. A New Aspect of Mathematical Method.Princeton: Princeton University Press. Rönnerman, K. (red). (2004) Aktionsforskning i praktiken – erfarenheter och reflektioner. Lund: Studentlitteratur. Skolinspektionen. (2010). Undervisningen i matematik i gymnasieskolan. Skolinspektionens rapport 2010:13. Stockholm: Skolinspektionen. Skolverket. (2000). Kursplaner för matematik. Stockholm: Skolverket (från http://www.skolverket.se/sb/d/726/a/13845/func/amnesplan/id/MA/titleId/Matematik och http://www.skolverket.se/sb/d/726/a/13845/func/kursplan/id/3202/titleId/MA1201%20-%20Matematik%20A 2011-01-04) Skolverket. (2010). Ämnesplan för matematik. Remissversion. Stockholm: Skolverket. Hämtat från http://www.skolverket.se/sb/d/3398 2011-01-03 Wyndhamn, J., Riesbeck, E., och Schoultz, J. (2000). Problemlösning som metafor och praktik. Studier av styrdokument och klassrumsverksamhet i matematik- och teknikundervisningen. Linköping: Linköpings universitet. Uppsatser: Edman, E. och Johansson, H. (2009) Problemlösning i matematik – en kvalitativ studie med fokus på de erfarna lärarnas syn på problemlösning, dess förhållande till kursplan och roll i undervisningen. Högskolan i Halmstad. Lindström, L. (2009) Matematiklärare om problemlösning – Åsikter och användning i undervisningen. Mälardalens högskola. Elisabeth Samuelsson PDAX51