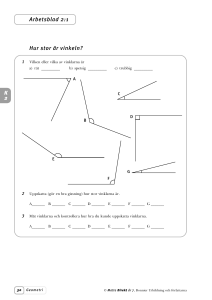
5. Geometri och argument

Geometri och
argument
Solkanonen i Åtvidaberg som tänds av solen kl.12.00. De röda linjerna visar tänkta
solstrålars väg till krutladdningen. Dvs inte ens ljusstrålar rör sig alltid i räta linjer.
1
2
3
4
5
6
Logik och matematik……………………………..
Empiriska vetenskaper…………………………..
Jordmätning………………………………………….
Den axiomatiska metoden……………………..
Rätvinkliga trianglar………………………………
Trigonometri…………………………………………
Klassisk geometri…………………………………
Konstruktioner……………………………………..
Modell ▪ Area- och volymskalan………………
Facit
2
6
14
15
24
30
35
48
51
53
Bilder: Akvareller av Ramon Cavaller. Foton s 1, 17, 36 och 37 Arne Flink. Illustrationer s
37, 38 och 39 Hans Hillerström. Geometriska konstruktioner, diagram och fotot Pantheon av
Nils-Göran Mattsson
© Författarna och Bokförlaget Borken, 2011
Geometri - 1
1. Logik och matematik
Logiken kännetecknas av regler med vars hjälp man drar (logiska) slutsatser ur en given mängd av satser (påståenden) eller kontrollerar om en
slutledning är giltig.
Man kan nu resonera deduktivt eller logiskt utan att uttryckligen nämna
alla de förutsättningar man gör för att komma fram till en viss slutsats.
Så gör man ofta i matematiken, där man ofta tar logiken som given och
låter bli att nämna, vilka logiska regler man förlitat sig på, då man dragit
slutsatser ur de rent matematiska förutsättningarna. I sådana fall sägs
man arbeta informellt. Ett av de första historiska exemplen på hur vetandet inom ett kunskapsområde kunde sammanfattas enligt ovan beskrivna
informella metod, är Euklides geometri. Han var verksam i Alexandria
omkring 300 f Kr. Euklides lärobok i geometri Elementa var grunden
för geometriundervisningen vid vissa skolor så sent som vid 1900-talets
början.
Några lärosatser hos Euklides, och andra matematiker som byggt upp
axiomatiska system, betraktas som axiom. Det finns inga bevis för dem
inom det axiomatiska systemet. Exempel på axiom eller postulat finns
under teoriavsnittet Den axiomatiska metoden.
Lite vardagslogik
Jämför de två slutledningarna:
• (premiss 1:) Om A äger produktionsmedel, så är han kapitalist och
(premiss 2:) A äger produktionsmedel.
medför (tesen:) A är kapitalist
• (premiss 1:) Om det brinner, så kommer brandkåren och
(premiss 2:) Det brinner.
medför (tesen:) Brandkåren kommer
De två ovan nämnda slutledningarna sägs vara deduktivt (=logiskt) giltiga.
Detta innebär att var och en som förstår innebörden av begreppen i de
två argumentationerna inte utan att motsäga sig själv kan bejaka premisserna samtidigt som han bestrider tesen. De två argumenteringarna kännetecknas av att tesen med nödvändighet följer ur premisserna. Argumenteringen är giltig. Därmed inte sagt att resonemangen är sakliga . Det kan
ju vara så att argumenten eller premisserna inte är sanna eller sannolika.
Geometri - 2
Premiss 1 i det andra fallet skulle kunna vara falskt. Brandkåren kommer
kanske inte, trots att det brinner. Man har kanske glömt att larma den.
Du ser kanske den stora likheten mellan de två argumenteringarna. Vi
säger att de har samma logiska form. Det är alltså själva de språkliga uttrycken ’om ..(förled).. så ..(efterled)..’ respektive ’och’ som i dessa
fall ger samma logiska form. Rent allmänt kan man säga att alla argumenteringar som har samma logiska form antingen är deduktivt giltiga
allihop eller också är ingen giltig.
Låt oss ta de två slutledningarna ovan för skilda tillämpningar av
slutledningsregeln modus ponens, vilket alltså innebär att man från en
"om...så…"-sats och förledet i "om...så…"-satsen härleder efterledet i
"om...så…"-satsen.
Vi skall nedan ge exempel på ett antal satslogiskt giltiga argumenteringar. Vi använder dessutom en symbol för begreppen medför eller
implicerar eller alltså. Symbolen är Þ
Negationsregeln
Exempel Det snöar. Þ Det är inte fallet att det inte snöar.
Disjunktionsregler
Exempel Det regnar. Þ Det regnar eller blåser.
(Han får brev på måndag eller också på tisdag.) och (Han får inte
brev på måndag.) Þ Han får brev på tisdag.
Konjunktionsregeln
Exempel Det blåser och snöar. Þ Det snöar
Implikationsregler (Vi har redan analyserat modus ponens.)
Exempel (Om det regnar, så stannar jag hemma.) och (Jag stannar
inte hemma.) Þ Det regnar inte. (Denna regel kallas modus tollens.)
Däremot gäller inte följande två slutledningar:
Om det regnar, så stannar jag hemma och Jag stannar hemma. Þ
Det regnar.
Om det regnar, så stannar jag hemma och Det regnar inte Þ Jag
stannar inte hemma
Geometri - 3
Ekvivalensregler
Om implikationen går i bägge riktningar som i följande matematiska
exempel så kan vi använda ekvivalenspilen.
Exempel [a < b Þ a + 3 < b + 3] men eftersom [a + 3 < b + 3 Þ
a < b] kan vi kortare skriva [a < b Û a + 3 < b + 3]
Kontraposition
Exempel Om denna figur är en cirkel, så är den också en ellips. Þ
Om figuren inte är en ellips, så är den inte heller en cirkel.
G1.1 Vilka av följande slutledningar är giltiga?
(a)
Jag går på bio eller teater. Jag går inte på bio.
Alltså går jag på teater.
(b)
Om Per är en skicklig schackspelare, så är Per logisk.
Per är en skicklig schackspelare. Alltså är Per logisk.
(c)
Om du gapar efter mycket, så skall du mista hela stycket.
Du har mist hela stycket. Alltså har du gapat efter mycket.
(d)
Om inte nativiteten i världen sjunker, kommer en katastrof att
inträffa. Alltså: Om en katastrof inte skall inträffa, måste
nativiteten i världen sjunka.
(e)
Handlingen är rätt, om handlingen medför överskott av lycka
för de flesta inblandade. Denna handling är orätt.
Alltså: den medför inte ett överskott av lycka för de flesta
inblandade.
(f)
Det varken blåser eller snöar. Alltså snöar det inte.
(g)
Det blir inte kallare eller också blir det regn. Det blir inte regn.
Alltså blir det kallare.
(h)
Om Carl Bildt inte högaktar Edmund Burke så är han inte
konservativ. Men Carl Bildt högaktar E. Burke.
Alltså är han konservativ.
Geometri - 4
(i)
Jan måste gå i borgen för Per, annars kan Per inte reda upp sin
ekonomi. Nu går Jan i borgen för Per.
Alltså kan Per reda upp sin ekonomi.
(j)
Om kärnkraften är farlig så skall vi inte använda oss av den.
Alltså: om kärnkraften inte är farlig så skall vi nyttja den.
(k)
Om figuren c är en cirkel så är det samtidigt en ellips.
Men c är inte en ellips. Alltså är det inte heller en cirkel.
G1.2
Är följande slutsatser logiska – använd din intuition!
Alla svenskar är filosofer.
Alla matematiker är filosofer.
Alltså är alla svenskar matematiker
a)
b)
Alla sanna socialister är agnostiker.
Några präster är sanna socialister.
Alltså finns det präster som är agnostiker.
c)
Det finns författare som är skådespelare.
Alla poeter är författare.
Alltså är några poeter skådespelare.
d)
Inga matematiker är politiker.
Inga politiker är logiker.
Alltså finns det inga matematiker som är logiker.
e)
Några studenter bär öronringar.
Några som bär öronringar är inte gay.
Alltså är några studenter inte gay.
Geometri - 5
2 Empiriska vetenskaper
De empiriska vetenskaperna har till uppgift att studera den verklighet vi
lever i. Detta innebär att man:
A samlar in fakta för att visa hur verkligheten ser ut.
B förklarar varför dessa fakta föreligger.
C använder detta vetande för att förutsäga vad som kommer att ske
eller vad som skulle ske om vissa fakta föreligger.
Vi skall komma ihåg att verksamheterna A, B och C inte försiggår så att
vi först gör A, sedan B och därefter C. Det brukar börja med att man vill
förklara vissa fakta som man utgår ifrån. Därefter gör man kanske en
gissning [ställer upp en hypotes] om vilken förklaring som är den riktiga
och som man vill pröva, vilket kanske ger anledning till att söka ytterligare
fakta. Om hypotesen visar sig felaktig då vi prövat den kanske vi börjar
leta efter nya fakta och ställer upp en ny hypotes [eller tvärtom ställer upp
en ny hypotes och letar fakta som kan bekräfta den].
A. Insamling av fakta
En forskare kan ha till sin enda uppgift att samla och systematisera fakta
(t ex en botanist som kartlägger floran i ett landskap och klassificerar
växter som han finner där). Vanligare är dock att han också arbetar vidare
med dessa fakta för att komma fram till en förklaring till varför de föreligger eller använda dem i förklaringar av andra fakta, som man tidigare
känt till och velat förklara. Det är dock inte helt oproblematiskt vad som
skall räknas som fakta. I vissa vetenskaper görs observationer under sådana betingelser att det kan vara svårt att avgöra om något är ett faktum
eller inte. Det kan också vara svårt att avgöra när man slutar att presentera
fakta och tolkning av fakta tar vid. Gör man en felaktig tolkning av fakta
kan ju en falsk hypotes synbarligen bli bekräftad, så det är viktigt att hålla
isär fakta och tolkningar och dessutom vara ytterst försiktig då man tolkar
fakta. Man har t ex iakttagit att ungar till djur av vissa arter, såsom änder,
följer sin mor efter födelsen. Man kan då tänkas ta det som ett faktum att
det finns en speciell bindning av medfödd art mellan just modern och
hennes ungar. Det har emellertid visat sig att ungarna likaväl kan präglas
på andra djur, människor eller t o m döda ting som attrapper, stövlar
Geometri - 6
m m och följa dessa i stället för modern. Antagandet av en speciell bindning mellan moder och ungar visar sig sålunda vara enbart en tolkning,
och dessutom en felaktig sådan, på grund av iakttagna fakta.
Hypotesprövning
Den hypotetisk-deduktiva metod
Utgångspunkten för uppställandet av en hypotes, ett antagande, är att
vetenskapsmannen står inför ett problem. Problemen kan vara av olika
slag. En zoolog kan vara intresserad av att veta om ett beteende han har
iakttagit hos en individ av en djurart är tillfälligt eller om alla djur i arten
beter sig på samma sätt i liknande situationer. Jane van Goodall iakttog
hur en schimpans stack ned ett grässtrå i en termitstack för att fiska upp
termiter. Genom ytterligare iakttagelser kunde hon dra slutsatsen att
redskapstillverkning och redskapsanvändning av detta och liknande slag
förekommer allmänt bland schimpanser. Detta är ett exempel på induktivt förfarande, men inom naturvetenskaperna förekommer även deduktiva resonemang. Så är t ex fallet när det gäller prövning av hypoteser om
orsaker till olika händelser och företeelser. Vi skall här redogöra för en
metod som används vid många tillfällen från enkla vardagssituationer
till komplicerade vetenskapliga resonemang.
Även i matematiken används ofta hypotesprövning. Vi anar att ett
upptäckt sammanhang, en hypotes, är giltig. Vi kan därefter nöja oss med
denna upptäckt, t ex medianerna i en triangel skär varandra i en punkt.
Vi kan även försöka bevisa vår hypotes med hjälp av tidigare bevisade
matematiska och logiska sanningar.
Men nu tar vi ett exempel ur vardagslivet för att beskriva metoden. Kalle
kommer ut på morgonen och finner att hans ena cykeldäck är tomt.
Han misstänker att det beror på att ventilgummit är dåligt, så han byter
detta mot ett nytt, pumpar däcket och åker till skolan. Det går bra, men
på rasten ser han att däcket är tomt igen. Han antar då att det gått hål på
slangen, och efter skolans slut byter han ut slangen mot en ny, och nu
håller slangen luft. Vad har Kalle gjort? Jo, först gjorde han ett antagande om orsaken till att däcket var tomt. Litet högtidligt kan vi säga att
han uppställde en hypotes H 1 .
Geometri - 7
H 1 : Däcket är tomt därför att ventilgummit är dåligt.
En naturlig följd av detta antagande blir att han också antar att ett byte
av ventilgummit löser hans problem. Litet annorlunda uttryckt kan vi
säga att hans hypotes H 1 har en testimplikation dvs en sats som följer ur
hypotesen och som beskriver ett sakförhållande, om vilket man direkt
kan konstatera ifall det föreligger eller inte. Testimplikationen är i det
här fallet T 1 .
T 1 : Byte av ventilgummit gör att däcket håller luft.
Nu visade det sig att byte av ventilgummi inte hjälpte, och att T 1 således
var falsk. Kalle kan då också dra slutsatsen att också hypotesen H 1 var
oriktig. Vi säger då att hypotesen H 1 är falsifierad. Vi kan ställa upp
resonemanget som en logisk slutledning (modus tollens). Vi har alltså
antagit att H 1 implicerar T 1. Vi finner att T 1 är falsk och drar slutsatsen
att H 1 är falsk:
(Om H 1 så T 1 ) och (Det är inte fallet att T 1 ) Þ
(Det är inte fallet att H 1 .)
Eftersom modus tollens är logiskt giltig, kan vi med säkerhet anta att
hypotesen är falsk. (Givet förstås att T 1 verkligen är en följd av H 1 och
att vi korrekt fastslagit att T 1 är falsk.)
Därefter antog Kalle en ny hypotes H 2 .
H 2 : Däcket är tomt därför att slangen är trasig.
Testimplikationen blir i detta fall:
T 2 : Byte av slang gör att däcket håller luft.
Geometri - 8
Nu visar det sig att T 2 uppfylls, och vi drar då slutsatsen att vi fått en
bekräftelse av hypotesen. Formellt kan vi ställa upp en slutledning av
samma slag som vi gjorde vid falsifieringen ovan:
(Om H 2 så T 2 ) och (T 2 ) Þ (H 2 )
Vi ser emellertid genast att detta inte är en logiskt giltig slutledning. Vi
har ju endast visat att ett nödvändigt villkor för hypotesens sanning
föreligger, inte att ett tillräckligt villkor för dess riktighet är för handen.
Vad vi på sin höjd kan säga är att testimplikationens riktighet ger en viss
grad av sannolikhet åt antagandet att hypotesen är riktig. Hur stor denna
sannolikhet är beror på hur många andra orsaker till att testimplikationen
förelåg det kan finnas i det aktuella fallet och hur sannolikt det är att någon
av dessa förekommit. Detta kan belysas med följande resonemang: När
Kalle bytte slangen bytte han ju också ventilen och därmed också ventilgummit igen. Det finns alltså en möjlighet att det var ventilgummits fel
att däcket var tomt, för också det nya ventilgummi som Kalle satte dit
kunde ju ha gått sönder. Så om Kalle är nyfiken kan han gå vidare och
göra ytterligare undersökningar för att få ytterligare bekräftelse av H 2
eller kanske rent av falsifiera den. Han kan t ex undersöka den gamla
slangen och se om den har något hål (dvs undersöka en ny testimplikation av H 2 som vi kan kalla T 2 ' som säger att vid en undersökning skall
det visa sig att slangen har ett hål). Om han hittar hålet är H 2 ytterligare
bekräftad. Skulle det däremot visa sig att slangen inte har något hål så
blir ju H 2 falsifierad och Kalle kanske övergår till att tro att H 1 var riktig
i alla fall.
Sammanfattar vi vad vi har sagt här får vi följande schema för hypotesprövning:
• Man uppställer en hypotes för att lösa ett bestämt problem.
• Man undersöker vilka testimplikationer hypotesen har. Ibland nöjer
man sig med att fastställa någon eller några av flera möjliga.
• Man fastställer genom undersökning om testimplikationerna eller
några av dem är sanna.
• I vissa fall, då hypotesen bekräftats, går man vidare för att genom
ytterligare undersökningar ge en ökad sannolikhet åt hypotesen eller
kanske tvingas överge den då en falsifierad testimplikation uppträder.
Geometri - 9
Minimikrav på vetenskapliga teorier
En hypotes eller teori är vetenskapligt godtagbar endast om den
uppfyller följande fem krav:
1. Motsägelsefrihetskravet verkar vid första påseende självklart. Logiken
visar att om en teori, som består av en mängd satser, innehåller satsen p
och dess negation: (Det är inte fallet att p) så kan vi härleda vilken sats
som helst ur teorin. En sådan teori är värdelös, eftersom den är riktig vad
som än är fallet i verkligheten.
2. Prövbarhetskravet innebär att teorin måste ha testimplikationer,
som kan prövas empiriskt. Att de kan prövas empiriskt innebär att man
kan göra iakttagelser eller experiment som visar om de är sanna eller
falska.
Då man säger att man skall kunna pröva en hypotes, menar man i regel
att det skall vara i princip möjligt att pröva den, även om det inte är
praktiskt möjligt att göra detta någonsin eller bara för tillfället. Detta
innebär att man skall kunna ange vilka observationer som skulle utvisa
om hypotesen är sann eller falsk. I den meningen var det i princip möjligt
att testa hypotesen att det finns liv på Mars innan man lyckades sända en
rymdfarkost dit, vilket gjorde hypotesen prövbar även praktiskt. Däremot
är det inte ens i princip möjligt att pröva Aristoteles teori att kroppar
faller till jorden, därför att de längtar till sin naturliga plats (jordytan).
Inte heller kan vi pröva hans förklaring till att vattnet följer med kolven
upp i ett pumprör, så att inget tomrum bildas under kolven, vilken gick
ut på att naturen har en avsky för tomrum.
3. Rimlighetskravet innebär att en teori inte får avvika från vad som är
allmänt accepterad och vedertagen kunskap. Man får inte anta någon
teori som strider mot vad som normalt antas vara bevisat bland
majoriteten av forskare. Naturligtvis är detta krav högst kontroversiellt.
4. Relevanskravet slutligen innebär att den hypotes eller teori man
uppställer måste förklara de fenomen den är till för att förklara. Detta
krav är allmänt accepterat.
5. Falsifierbarhetskravet Karl Popper (1902-1994) som föddes i Wien
måste räknas som en av 1900-talet främsta vetenskapsfilosofer. Popper
Geometri - 10
ansåg att det avgörande kravet på ett vetenskapligt påstående är
falsifierbarhet. Ett påstående är vetenskapligt bara om det kan falsifieras
dvs att man kan ange de betingelser under vilka satsen kan visas vara
falsk. Popper menar också att teorier med en hög "falsifierbarhetsgrad" är
att föredra framför sådana med en lägre. Falsifierbarhetsgraden ökar med
antalet möjliga påståenden som, om de vore sanna, skulle göra teorin
falsk. "Alla katter är grå" har en hög falsifierbarhetsgrad, eftersom den
kan vederläggas av: "Murre är brun", "Bianca är vit", "Misse är svart"
osv, men påståendet: "Murre är grå" har en låg falsifierbarhetsgrad,
eftersom den bara kan falsifieras av satser som säger att Murre har en
annan färg än grå, och dessa är mycket färre än i det tidigare fallet.
V2.1 En man knuffar ett barn i havet för att dränka det och en annan
man offrar sitt liv för att rädda ett barn som håller på att drunkna. Enligt psykologen Adler lider den förste mannen av mindervärdeskänslor; dessa känslor får mannen att bevisa att han kan
begå ett brott. Den andre mannen, som också lider av mindervärdeskomplex (detta komplex är enligt Adler grunden till allt
mänskligt beteende), har ett stort behov att visa att han vågade
rädda barnet. Kommentera dessa två fall utifrån falsifierbarhetsprincipen.
V2.2 (ur Konrad Marc-Wogau, Freuds psykoanalys) ”En del har gjort
gällande att psykoanalysen inför teser som är sådana att inga
erfarenheter kan falsifiera dem. Det antas t ex att en patients
neurotiska besvär orsakas av Oidpuskomplexet; han hyser omedvetet hatkänslor mot fadern. Om nu patienten visar vördnad för
eller kärlek till fadern, så säger psykoanalytikern att patienten på
grund av sin fientliga inställning till fadern och omedvetna rädsla
för honom i sitt beteende döljer sina egentliga känslor.” Försök
att visa att falsifierbarhetskriteriet trots allt kan tillämpas på
Freuds teori om Oidupuskomplexet.
Geometri - 11
V2.3 Det klassiska exemplet på hypotesprövning:
Ignaz Semmelweiss arbetade under 1800talets mitt som förlossningsläkare i Wien.
Dödligheten i barnsängsfeber var mycket
högre på hans avdelning än på sjukhusets
andra avdelning. Genom skarpsinne lyckades han ta reda på orsakerna till skillnaden
i dödlighet vid de två avdelningarna. Sjukdomen kunde även bekämpas av honom.
Semmelweiss formulerade några hypoteser
för att utröna vilken som bäst klarade test.
(i)
Överbeläggning på Semmelweiss avdelning är orsak till barn-
sängsfeber.
(ii)
Skillnaden mellan de två avdelningarna med avseende på dieten
orsakar sjukdomen.
(iii) Skillnaden mellan avdelningarna med avseende på vården
orsakar sjukdomen.
(iv) De medicinare som undersökte kvinnorna på Semmelweiss
avdelning var hårdhäntare än barnmorskorna på den andra
avdelningen.
(v)
Prästen som skulle ge de drabbade sista smörjelsen måste passera
Semmelweiss avdelning varvid dessa kvinnor blev skrämda .
(vi) Kvinnornas olika födelseställning, rygg- och sidoläge, orsakar
barnsängsfeber.
(vii) Barnsängsfeber beror på överföring av ”likstoff” från människor
som obducerats (Semmelweiss fick idén till denna hypotes när en
kollega till honom dog i symptom som liknade barnsängsfeber efter
det att han skurit sig under en obduktion. Semmelweiss kom då att
tänka på att några av hans medicinstuderande deltog i obduktioner
innan arbetsdagen satte igång på förlossningsavdelningen.)
(viii) Förruttnelseprodukter från levande eller döda människor kan
orsaka barnsängsfeber.
a)
Formulera testimplikationer till hypoteserna ovan så att
hypotesen blir falsfierad eller verifierad.
b)
Ger falsifieringen en logiskt giltig slutledning?
c)
Ger verifieringen en logiskt giltig slutledning?
Geometri - 12
Fundera på dessa två problem!
A. Hur skall en färjkarl frakta över en varg, ett får och
ett kålhuvud över en flod? Han måste utgå ifrån att
vargen utan tillsyn skulle äta upp fåret och att fåret
utan vakt skulle äta upp kålhuvudet. Vidare kan han
bara frakta ett av de tre objekten samtidigt.
B. Antag att vi har två dörrar, där den ena leder till
säkerhet och den andra till en säker död. Dörrarna
vaktas av en sanningssägare och den andra av en
lögnare. Du vet inte vem som är vad. Du får bara
ställa en fråga för att lista ut vilken dörr som leder till
säkerheten. Vilken fråga ställer du?
Geometri - 13
Teori ▪ Jordmätning
Man kan säga att geometri handlar om två saker. För det första handlar
geometrin om verkligheten som omger oss. Det runda tornet, pyramidens form, de spännande formerna som bygger upp en målning av
Picasso, solstrålen som går rätlinjigt fram, planeternas ellipsformade
banor runt solen. Listan kan göras lång. Man anser att människan
började utveckla kunnandet i geometri när det uppstod behov av att
mäta upp landområden (sträckor, areor och även volymer) och när
byggnadstekniken utvecklades i de tidiga högkulturerna i Egypten och
Babylonien. Ordet geometri betyder egentligen ”jordmätning”.
Samtidigt som hantverkare och jordbrukare i sin vardagliga verksamhet
lärde sig mer om vinklar och figurer och hur de förhöll sig till varandra
började filosofer och tänkare studera de geometriska begreppen för deras
egen skull. Det uppkom en ren geometri som är rent formell och bara
handlar om de olika geometriska figurernas egenskaper. Men när
geometriska begrepp används i det dagliga livet och i naturvetenskap,
konst och arkitektur är det inte den teoretiska rena geometrin utan
fysikalisk geometri. Den kan sägas handla om vår egen tredimensionella
värld. När vi vardagsmänniskor använder de geometriska begreppen, då
kan en punkt i ett sammanhang betyda skärningen mellan två korslagda
hårstrån och i ett annat jordklotets medelpunkt. En rät linje kan både
vara snöret till lodet man använder när man tapetserar och en ljusstråles
väg. De geometriska satserna som till exempel den kanske mest kända
Pythagoras sats har formulerats utifrån praktisk erfarenhet och teoretisk
tankemöda i samverkan. Orsaken till att människorna har visat geometrin
så stort intresse under flera tusen år är att den har visat sig vara så praktiskt användbar. Idag vet vi att geometrin måste och har utvecklas för att
kunna beskriva universum i stort. Den vanliga euklidiska geometrin som
vi nu ska studera fungerar mycket bra i vår vardagliga värld. Men frågan
är om den är tillräcklig för de stora avstånden i världsrymden.
Geometri - 14
3 Den axiomatiska metoden
Teori ▪ Den axiomatiska metoden
Vad innehåller då Euklides Elementa? Den består av 13 ”böcker” eller
kapitel. Den startar med 23 definitioner, 5 postulat och 5 axiom och
därefter bevisar han 465 satser.
Låt oss börja med postulaten d v s antaganden som bara tillhör kunskapsområdet geometri. Idag skulle vi även kalla dessa för axiom. Vi formulerar
dem i moderna versioner.
Postulat 1. Om vi har två olika punkter så finns den en och endast en
rät linje som passerar bägge.
Postulat 2. Det går att obegränsat förlänga en begränsad rät linje
(sträckan AB).
Postulat 3. Om vi utgår från två olika punkter,
O och A så finns det en cirkel med medelpunkt i O och radie OA.
Postulat 5. Om en rät linje t skär två räta linjer, l och m, så att de inre
vinklarna på samma sida α och β, tillsammans är mindre än två räta
vinklar, så möts de två linjerna, om de dras ut oändligt, på den sida på
vilken vinklarna är mindre än två räta.
Den finns en med denna version ekvivalent formulering av postulatet:
Postulat 5’ Om vi utgår från en rät linje l och en punkt P som inte
ligger på l, så finns det högst en linje genom P som är parallell (= inte
skär) l.
Geometri - 15
Naturligtvis finns det minst en också och därmed exakt en, men detta
kunde redan Euklides bevisa ur de andra postulaten.
Vilka är då de generella axiomen?
Axiom 1. a = c och b = c medför att a = b
Axiom 2. a = b medför att a + c = b + c
Axiom 3. a = b medför att a – c = b – c
Axiom 4. Storheter som sammanfaller med varandra är lika varandra.
Axiom 5. Det hela är större än delen. (T ex längder, areor och volymer)
I elementa beskriver Euklides ofta
hur man löser uppgifter med passare
och ograderad linjal. Denna
lösning måste följa regler som
• Starta med ett antal givna
punkter!
• De givna punkterna (t ex de blåa)
kan användas för att (i ) dra en
linje genom punkterna och
(ii ) rita en cirkel med en punkt
(den röda) som medelpunkt och
som går genom den andra (också
röd) punkten.
(iii ) Konstruktion måste kunna
ha avslutats efter ett ändligt antal
steg av typ (i ) och (ii )
Den som bygger upp ett axiomatiskt system använder sig av vissa grundbegrepp, t ex punkt medan andra begrepp definieras med hjälp av de
odefinierade t ex
Def.1. En punkt är det som inte har någon del.
Def.2. En linje är längd utan bredd.
Def.3. En sträckas ändar är punkter.
Def.5. En yta är det som endast har längd och bredd.
Def.6. Kanterna till en yta är linjer.
Geometri - 16
Om man tycker att dessa förklaringar eller definitioner är underliga så
kan man helt enkelt låta våra grundbegrepp vara oförklarade. Vi utnyttjar bara begreppens egenskaper och relationer som de är uttryckta i
axiomen.
Detta var t ex matematikern David Hilberts (1862 – 1943) syn på
axiomatiska system.
Många har påpekat de logiska bristerna i Euklides axiomatiska system
och 1899 publicerade Hilbert en moderniserad version av Elementa,
Grundlagen der Geometri , som fortfarande är oöverträffad.
Teori ▪ Vinklar
Två strålar som utgår från samma punkt A delar planet i två områden
som kallas vinklar . Strålarna kallas vinkelben och punkten A vinkelspets.
Vinklarna har markerats i figuren med bokstäverna u och v. Vinklarna
mäts i grader och enheten är en grad som skrivs 1°. En grad är 1/360 av
ett helt varv. Även det är en vinkel som är 360°. Ett halvt varv är 180°.
En vinkel som är större än 90° kallas en trubbig vinkel medan en vinkel
mindre än 90° kallas spetsig. Vinklar på 90° kallas räta.
Postulat i denna lärobok: Vertikalvinklar (t ex α och β eller γ och δ i
figuren nedan) är lika stora.
Geometri - 17
Låt oss nu bevisa: Sidovinkelsatsen.
Sidovinklar (t ex α + δ i figuren ovan) är tillsammans 180°.
Enligt postulat ovan är α = β samt γ = δ
Vi vet dessutom att α + β + γ + δ = 360°
Þ (synonymer till piltecknet: medför, ger, implicerar)
2α + 2 δ = 360° (eftersom α = β samt γ = δ) Þ α + δ = 180° V.S.B
Den hypotetiskt deduktiva (HD) metoden hos Popper liknar
den axiomatiska metoden genom att man så att säga går uppifrån nedåt
och endast använder logiska slutledningar. Såväl den axiomatiska
metoden som HD godkänner endast deduktiv logik.
Det finns emellertid stora skillnader. Rationalisterna tror, att man
genom rent förnuftsmässigt tänkande kan finna sanna och evidenta
axiom. Popper däremot menar att historien visar att detta är omöjligt.
De axiom som man under århundraden tagit som evidenta har ofta
senare visat sig felaktiga. Vi kan alltså aldrig vara säkra på att ett axiom
om verkligheten är sant enbart på förnuftsmässiga grunder, dvs enbart
därför att vi tycker att de absolut måste vara sanna.
Enligt Popper är varje axiom om verkligheten i själva verket en hypotes,
dvs en gissning. I stället för att försöka med den omöjliga uppgiften att
finna evidenta axiom bör forskaren göra något mycket mer anspråkslöst.
Han bör utarbeta fruktbara hypoteser. Det ligger sålunda i forskningens
natur enligt Popper att forskaren så att säga måste gissa sig fram mot allt
bättre kunskaper. Men gissningar är dels osäkra och dels förutsätter de
fantasi, kreativitet, intuition.
Enligt Popper finns det ingen metod som kan leda fram till bevisade,
orubbliga teorier. Det finns ingen metod som gör att teorier förvandlas
till fakta. Enligt Popper är vetenskapens teorier sålunda varken bevisade
sanningar eller ytterst sannolika. Liksom alla realister anser han vetenskapens grundläggande mål vara att förklara vår värld. Men han ser
förklarandet som en oavslutad process. Målet är att hela tiden sträva
efter allt bättre förklaringar.
Geometri - 18
G3.1
Hur stor är vinkeln v vid den räta linjen? Är vinkeln spetsig
eller trubbig?
G3.2
Hur stor är vinkeln mellan tim- och minutvisaren
kl.16.00 b) kl. 22.00?
a)
G3.3
a)
V3.4
a)
b)
V3.5
Hur stor är den vinkel som upptar
ett fjärdedels varv b) ett halvt varv
c) ett åttondels varv
Hur stor är vinkeln mellan väderstrecken
norr och öster
c) norr och nordöst
norr och söder
d) norr och nordnordväst
Ett helt varv består av fem vinklar, där den andra vinkeln är
dubbelt så stor som den första, den tredje är dubbelt så stor
som den andra osv. Beräkna den minsta vinkelns storlek.
Om A, B, C, D och E är punkter
i ett plan som bildar sträckorna
AB, BC, CD, DE och EA, så
utgör dessa ett område ABCDE
som kallas en polygon. I vårt fall
har polygonen fem hörn och
kallas därför en femhörning.
Polygoner kan ha vilket antal
hörn som helst större än eller lika
med 3. Har polygonen tre hörn
kallas den en triangel.
Geometri - 19
En linje som skär två eller flera
räta linjer kallas en transversal. Vi
markerar vinklarna med de
grekiska bokstäverna α, β, γ och
δ. Vinklarna α 1 och α2 , β 1 och
β 2 , γ 1 och γ 2 samt δ 1 och δ 2 är
parvis likbelägna vinklar . α 1 och
γ 1 , β 1 och δ 1 kallas som vi
tidigare nämnt vertikalvinklar .
Ge exempel på flera par av
vinklar som är likbelägna vinklar
respektive vertikalvinklar.
G3.6
Bevisa att likbelägna vinklar till parallella linjer är lika stora.
Använd dig av bl a postulat 5 för att genomföra en deduktiv
argumentering.
G3.7
Till en vinkel u och dess sidovinkel v dras bisektriserna b 1 och
b 2 . (En bisektris delar en vinkel mitt itu.) Gör en tydlig deduktiv
härledning av hur stor vinkeln är mellan bisektriserna.
Geometri - 20
Teori ▪ Trianglar
Låt oss se på Euklides bevis för att triangelns vinkelsumma är 180°.
Vi skall informellt bevisa att α + β + γ = 180°
Vi gör en konstruktion för beviset, en linje parallell med sidan AB som
går genom vinkelspetsen C.
u + γ + v = 180° (Satsen om sidovinklar)
Eftersom u = α (alternatvinklar vid parallella linjer) och v = β
Þ α + β + γ = u + γ + v = 180°
V.S.B.
G3.8
Bestäm vinkeln γ i triangeln ABC om triangelns övriga vinklar
är 63,5° och 72,5°.
G3.9
Bevisa informellt Yttervinkelsatsen: Yttervinkeln δ är lika
med summan av de motstående inre vinklarna, α och γ.
Geometri - 21
Definitioner
I en likbent triangel är två sidor lika långa. Den tredje sidan kallas
basen. I en liksidig triangel är alla sidor lika långa.
G3.10 Bevisa att en fyrhörnings vinkelsumma är 360°. Om du ritar
en diagonal till fyrhörningen så blir det enklare att bevisa
satsen.
G3.11 I en triangel är en vinkel 11° större än den minsta och en vinkel
31° större än den minsta. Hur stora är triangelns vinklar?
G3.12 I en likbent triangel är en vinkel 30° mindre än en annan.
Beräkna triangelns vinklar. Kan uppgiften ge fler än en lösning?
G3.13 I en likbent triangel är var och en av de lika stora vinklarna fyra
gånger så stor som den tredje. Beräkna triangelns vinklar.
V3.14 I en triangel förhåller sig vinklarna till varandra som 3:4:5.
Beräkna triangelns vinklar.
V3.15 I en likbent triangel ABC är vinklarna vid A och B lika stora.
Yttervinkeln vid C är 130°. Beräkna triangelns vinklar.
V3.16 Vilka värden har yttervinklarna till en rätvinklig likbent
triangel?
V3.17 I en triangel med vinklarna 63°, 27° och 90° dras bisektrisen
till den största vinkeln. Bisektrisen delar den större triangeln i
två nya trianglar. Beräkna vinklarna i dessa trianglar. (Ledning:
Bisektrisen till en vinkel är en linje som delar denna mitt itu.)
Geometri - 22
V3.18
En trubbig triangel är en triangel, som har en trubbig vinkel
(vinkel större än 90º). Visa att det inte kan finnas två trubbiga
vinklar i en triangel.
V3.19 Visa att summan av yttervinklarna till en triangel är 360° .
V3.20 Det är omöjligt att med passare och linjal dela en given vinkel i
tre lika stora vinklar. Apparaten nedan klarar i alla fall av detta.
Sträckorna OB, AB och AC är lika långa. Punkterna O och B
är fixerade men vridbara kring sina axlar på den horisontella
stången OBC. Om man lyfter eller sänker punkten P på
stången OAP, så förflyttar sig punkten A i en skåra på denna
stång, samtidigt som punkten C rör sig i en skåra på stången
OBC. Visa att vinkeln α är en tredjedel av vinkeln β. Varför
duger inte detta som ett konstruktinsbevis för vinkelns tredelning?
Geometri - 23
4 Rätvinkliga trianglar
M atematiken i historien
Allt är tal
I staden Kroton i Syditalien levde på 500-talet f.Kr.
Pythagoras. Pythagoras ledde en sekt av mystiker som sysslade med
talteori och geometri, astronomi, religion och politik. Även kvinnor var
välkomna i denna sekt. Den mest kända är Theano från Kroton som
gifte sig med Pythagoras. Hon gav ut skrifter i matematik och naturfilosofi.
Enligt dessa mystiker är människan delad i en odödlig själ och en kropp,
som pythagoréerna liknar vid ett fängelse eller en grav. Människans själ
kunde renas och befrias från kroppen genom matematiska studier.
Teori ▪ Om a2 + b2 = c2 så är triangeln rätvinklig
Redan under antiken kände man till en speciell sorts trianglar som vi nu
kallar egyptiska trianglar. En triangel med sidorna 3, 4 och 5 längdenheter
är en sådan. Man kände tidigt till att sådana trianglar var rätvinkliga och
att summan av de två mindre sidornas kvadrater (i vårt fall 32 + 42 = 9 +
16 = 25) är lika med den längre sidans kvadrat 52 (=25).
Snickaren, som vill skapa ett rum
med räta vinklar, använder sig av
detta samband. Han sätter kanske av
tre meter längs den ena väggen och
gör där en markering. Därefter
markerar han fyra meter efter den
andra väggen. Om nu sträckan
mellan dessa markeringar är fem
meter så är hörnet rätvinkligt.
Geometri - 24
De sidor, som bildar den räta vinkeln, kallas kateter (a och b i figuren)
(gr. cathetos, vinkelrät linje, ’lodlina’) och den tredje sidan, som står mittemot det räta vinkeln, kallas hypotenusa (gr. hypoteinousa, som sträcker sig
under). Dessa visa personer kände alltså till: om a 2 + b2 = c2 så är
triangeln rätvinklig. Detta användbara samband kallas Pythagoras sats.
Modell ▪ Om a2 + b2 = c2 så är triangeln rätvinklig
Exempel Är trianglarna med nedanstående sidor rätvinkliga?
a) 5, 12 och 13 cm
b) 9, 12 och 14 cm
Lösning Vi beräknar summan av kvadraterna på de två kortaste sidorna
i de två fallen:
a) 52 +122 =25+144=169
b) 92 +122 =81+144=225
Kvadraten på den längsta sidan i de två fallen är:
a) 132 =169
b) 142 =256
2
2
2
Alltså är a + b = c endast i det första fallet, och endast denna triangel är
rätvinklig.
G4.1
Du har byggt ett rektangulärt rum, där sidorna är 418, 240,
418 och 240 cm. Du mäter avståndet mellan två motstående
hörn till 481 cm. Är du nöjd med vad du åstadkommit?
Fundera på detta!
Eftersom triangeln med sidorna 5, 12 och 13 cm är rätvinklig
så kan du enkelt hitta oändligt många trianglar utifrån denna
5-12-13 triangel som är rätvinkliga, hur?
Geometri - 25
Teori ▪ Om en triangel är rätvinklig så är a2 + b2 = c2
Triangeln är rätvinklig Þ a2 + b2 = c2
Låt oss rita en kvadrat med sidlängden
(a + b). Vi ritar en fyrhörning inuti
denna kvadrat med hörnen i de
punkter som delar den större
kvadratens sidor i sträckorna a
respektive b. Rita själv en kvadrat
enligt dessa instruktioner. Även denna
fyrhörning blir en kvadrat med sidor
som vi kallar c.
Arean av den stora kvadraten kan vi skriva på två olika sätt:
(a + b)(a + b) = a2 + 2ab + b2
ab
4⋅
+ c2 = 2ab + c2 Varför?
2
Alltså är a2 + 2ab + b2 = 2ab + c2 som kan förenklas till a2 + b2 = c2.
(Vilket aritmetiskt axiom på sidan 16 har vi använt?)
Vi har alltså bevisat: Om en triangel är rätvinklig så är summan av
kvadraterna på kateterna lika med kvadraten på hypotenusan.
Detta är Pythagoras sats: Om en triangel är rätvinklig så a 2+b2 = c2
Vi har tidigare formulerat satsen:”Om a 2 + b2 = c2 så är triangeln
rätvinklig.”
Av detta följer att vi kan skriva den logiskt korrekta formuleringen:
En triangel är rätvinklig om och endast om a 2 + b2 = c2.
En triangel är rätvinklig Û a 2 + b2 = c2
Geometri - 26
Modell ▪ Om en triangel är rätvinklig så är a2 + b2 = c2
Exempel Beräkna diagonalen i rektangel vars sidor är 3,7 m och 5,2 m.
Lösning Eftersom sidorna är vinkelräta mot varandra, så bildar två
närliggande sidor och diagonalen en rätvinklig triangel. Vi antar att
diagonalen har längden d m. Pythagoras sats ger d 2 =3,72 + 5,22.
d ≈ ±6,4 Eftersom en sträcka är ett positivt tal förkastas den negativa
roten. Alltså är d ≈ 6,4. Diagonalen är 6,4 m.
G4.2
En snickare vill vara säker på att hörnet i ett rum blir rätvinkligt. Han mäter därför upp 1,5 m längs ena väggen och 2 m
längs den andra och gör markeringar på dessa ställen. Hur långt
skall det vara mellan dessa markeringar för att hörnet skall vara
rätvinkligt?
G4.3
I en rätvinklig triangel är ena kateten 7 cm längre än den andra.
Hur långa är kateterna om hypotenusan är 13 cm?
(Ledning: Båda kateternas längder är heltal.)
G4.4
Skärmens diagonal på en bärbar dator är 12,1 tum där
1 tum = 2,54 cm. Skärmens upplösning är 800 × 600 pixlar.
Detta innebär att skärmen rymmer 800 bildpunkter horisontellt och 600 vertikalt. Hur många pixlar finns på skärmen?
Ange svaret i grundpotensform och med lämpligt prefix.
Hur långa är skärmens sidor om en pixel är lika hög som bred?
V4.5
Tore, som är konstnär,
tänker fullända sitt
senaste verk med en
rätvinklig triangel som
han ska göra av en järnstång med längden 120
cm. Hur långa blir
triangelns sidor om
kateterna skall förhålla
sig som 5:12?
Geometri - 27
V4.6 Bara ett av världens sju
underverk hade en rent
praktisk funktion, nämligen fyren på Faros i
Alexandria. Denna fyr var
på sin tid jordens högsta
byggnad. Ljuset från elden
på dess topp kunde enligt
legenden synas många mil
till havs, genom att det
reflekterades i speglar. Det
sades också att man kunde
bränna fiendens skepp när
de närmade sig kusten
genom att solens strålar
reflekterades i fyrens speglar. Enligt en besökare år
1166 var fyren byggd i tre
steg. Det första steget var
kvadratiskt med en höjd på
55,9 m med en cylindrisk
kärna. Det andra steget var
åttkantigt med sidlängden
18,30 m och höjden 27,45
m. Det tredje steget slutligen var cylindriskt med
höjden 7,30 m. Fyrens
totala höjd inklusive dess
fundament var 117 m. Hur
långt ut kunde man se
fyrens sken om jordens
radie är 638 mil?
Geometri - 28
V4.7
Utför följande konstruktion. Rita
en vertikal sträcka AB med längden 1 längdenhet. Dra en sträcka
vinkelrätt mot den första sträckan
i dess ändpunkt B. Sträckan skall
vara en halv längdenhet.
Fullborda en rätvinklig triangel.
Rita en cirkelbåge med den
kortare sträckan som radie och
medelpunkten i det spetsiga
triangelhörnet. Denna båge skär
hypotenusan i en punkt Q. Dra
en ny cirkelbåge med radien AQ
och medelpunkt A. Den skär den
horisontella kateten i punkten P.
Visa att
AP 1  5
. Vi har de
BP
2
lat sträckan i det s k gyllene snittet.
V4.8 En dag säger Julia till sin mamma medan de arbetar i sin vackra
rektangulära trädgård. ”Det är 20 m kortare sträcka till trädgårdens motsatta hörn längs diagonalen än längs två av dess sidor.”
En sida är 60 m lång. Hur lång är den andra sidan?
Geometri - 29
5 Trigonometri
M atematiken i historien
Trigonometri handlar om sidor och vinklar i trianglar. Denna gren
av matematiken utvecklades för att göra det möjligt att utföra beräkningar
i astronomi och geografi. Idag är trigonometri ett viktigt hjälpmedel i
många grenar av matematik och naturvetenskap.
Enligt filosofen Aristoteles (300-talet f Kr) har universum en sfärisk form.
Planeterna rör sig i olika sfärer och jorden ligger stilla i centrum. Den
högsta är fixstjärnesfären. Gud är den kraft som håller igång universums
rotation. Denna rörelse fortplantas nedåt till de andra sfärerna som innehåller de då kända planeterna. Den här formulerade synen på universum
var tillsammans med Ptolemaios (100-talet e Kr) syn de vanligaste. Den
typ av trigonometri som behövdes för att förstå de olika himlakropparnas och stjärnornas positioner på
himlavalvet kallas sfärisk trigonometri
och det var den som först utvecklades.
I våra dagar börjar vi med att studera
plan trigonometri.
Trigonometriska tabeller skapades för
mer än två tusen år sedan för att kunna göra astronomiska beräkningar.
Ptolemaios använde trigonometriska
tabeller i sitt verk Geografi. Det berättas också att Columbus hade med sig
sådana tabeller på sin färd till den nya
världen.
Almagest är en stor handbok i astronomi
och matematik som gavs ut år 140 av
Ptolemaios i Alexandria. Verket är i 13
band.
Geometri - 30
Teori ▪ Rätvinkliga trianglar
Man utgår från rätvinkliga
trianglar när man studerar
trigonometri. Vi använder
detta beteckningssystem: En
rätvinklig triangel ABC har
sina hörn i punkterna A, B
och C. Sidorna a, b och c
står mot hörnen A, B och C
med vinklarna α, β och γ.
Sidan c är den längsta och
står mot den räta vinkeln vid
C. Den sidan kallas hypotenusa. De två övriga sidorna
a och b kallas kateter.
Beräkningar i rätvinkliga trianglar
Vid beräkningar i rätvinkliga trianglar har man nytta av vissa kvoter. De
b
a a
är
,
och . Dessa tre kvoter är så vanliga i trigonometrin att det
c
b c
a
fått egna namn: kallas tangens för vinkeln α eller bara tangens α. Den
b
kvoten skrivs tanα . De övriga kvoternas namn står i tabellen nedan.
tangens för vinkeln α
sinus för vinkeln α
cosinus för vinkeln α
motstående kateten
a
=
närliggande kateten
b
motstående kateten
a
sin α =
=
hypotenusan
c
närliggande kateten
b
cos α =
=
hypotenusan
c
tan α =
Eftersom varje värde på α i de tre fallen ger precis ett värde på tanα,
sinα och cosα beskriver de var för sig en funktion: y = tan α, y = sin α
och y = cos α.
Geometri - 31
Modell ▪ En sida och en vinkel är kända i en
rätvinklig triangel
Exempel med lösning
Låt oss först se på ett fall där sidan a = 14 och vinkeln α = 41°. Enligt
våra definitioner på sinus, cosinus och tangens är:
14
14
tan 41° =
och sin 41° =
b
c
14
14
Dessa två ekvationer kan skrivas: b =
och c =
. Lär dig

tan 41
sin 41
hur din räknare fungerar. Kanske gäller detta: 14 [ ÷][ tan] 41 [=].
Kontrollera att du får svaret b = 16,1 och c = 21, 3.
G5.1
Beräkna de okända sidorna i följande rätvinkliga trianglar
(beteckningar enligt figur på sidan 31).
a) α = 37°, b = 23 cm b) α = 74°, c = 23 cm
c) α = 13°, a = 23 cm.
G5.2
Beräkna de obekanta sidorna i nedanstående rätvinkliga
triangel.
G5.3
Beräkna de lika långa sidorna i nedanstående likbenta triangel.
Geometri - 32
Modell ▪ Två sidor är kända i en rätvinklig triangel
Exempel med lösning
Här känner vi två sidor och kan då beräkna den tredje sidan.
Sidan a = 10 l.e. och sidan b = 24 l.e.
Vi använder Pythagoras sats c2 = a2 + b2 och får 102 + 242 = 100 + 576 =
=676 = 262. Alltså är c = 26.
10
10
24
Alltså är tan α =
, sin α =
och cos α =
.
24
26
26
Den obekanta vinkeln α kan fås på tre olika sätt. Med knappen
–1
[ARCTAN] eller [tan ] fås den vinkel vars tangensvärde är det som
matas in. [ARCTAN] (10 [÷] 24) Kontrollera att du får svaret 22,6°.
G5.4
a)
b)
c)
Beräkna de obekanta vinklarna i rätvinkliga trianglar som har
följande sidor.
a = 15 cm och b = 23 cm
a = 7 cm och c = 23 cm
b = 11 cm och c = 23 cm
G5.5
Beräkna de obekanta vinklarna i denna triangel.
G5.6
Beräkna vinklarna i den likbenta triangeln.
Geometri - 33
G5.7
I en triangel ABC är A = 30° och B = 45°, och höjden från C
mot sidan AB är 3,22 cm lång. Beräkna längden av sträckan
AB.
G5.8
En 15 m hög steg är rest mot en byggnad. Stegens översta del
befinner sig 11 m från marken. Beräkna stegens lutning mot
väggen.
V5.9
Från ett skepp syns en fyr under vinkeln 3,5°. Fyrens höjd är
70 m över havsytan. Hur långt är det till fyren?
Pantheon i Rom Vårdagjämningen och höstdagjämningen är de
två tillfällen på året då dag och natt är lika långa. Bilderna nedan av
Pantheon nedan visar ett cirkulärt tempel byggt av kejsar Hadrianus 120
e Kr. Ovanpå det cirkulära cylindern reser sig en halvklotformig övre del
med radien 21,65 m, och med samma mått som höjden på den cirkulära
cylindern. Längst upp på Pantheon finns ett cirkulärt hål, okularet, som
släpper in solljuset. Vid vintersolståndet bildar de ljusstrålar som passerar
toppen av Pantheon 65 graders vinkel med lodlinjen. Vid sommarsolståndet är denna vinkel 19° och vid vår- och höstdagjämning 48°.
V5.10 Når solstrålarna som passerar okularet i Pantheon i Rom
byggnadens golv vid någon tidpunkt på året?
Geometri - 34
6 Klassisk geometri
Teori ▪ Kongruens
Om vi använder oss av begreppen translation (förskjutning),
rotation och spegling kan vi påstå
• Om två polygoner kan fås att täcka varandra fullständigt genom
dessa förflyttningar så sägs polygonerna vara kongruenta.
Antag att vi har två trianglar ΔABC och ΔKLM sådana att
(1) |AB = |KL|
(2) |BC| = |LM|
(3) |AC| = |KM|
(5) ^ BCA = ^ LMK
(4) ^ ABC = ^ KLM
(6)
^ CAB = ^ MKL
[I detta sammanhang utläses symbolerna
^ och Δ: vinkeln och triangeln]
Vi kan genom förflyttning få ΔKLM att fullständigt sammanfalla med
ΔABC. Detta innebär att trianglarna är kongruenta.
De ovan nämnda sex likheterna är inte oberoende av varandra. Vi kan
inse att redan om |AB = |KL|, |AC| = |KM| och ^ CAB =
^ MKL så är
trianglarna kongruenta. Detta fall kallade Euklides för första kongruensfallet. Hilbert använde sig av formuleringen som ett axiom i sin geometri.
Geometri - 35
Första kongruensfallet gäller alltså för följande ordning på sidor och
vinklar: SVS. Ger VVV (de tre vinklarna är lika stora), SSS (de tre
sidorna är lika stora) eller VSV kongruenta trianglar?
G6.1
Ge exempel på några bokstäver som kan roteras eller speglas
och som då förblir samma bokstav.
G6.2
Hur många längdenheter måste ett bord translateras för att
högra främre benet skall få de nya koordinaterna (1, 2) utifrån
(9, -1)?
G6.3
Konstruera en triangel med passare och linjal om du känner till
två sträckor och en vinkel dvs du får använda dig av figurerna
nedan.
G6.4
Vad är en bisektris till en vinkel? Konstruera bisektriserna till
vinklarna i en triangel med hjälp av en passare och linjal. Vilka
hypoteser kan du dra av resultatet? Hoppas att bilden nedan
ger lite ledning till att konstruera en bisektris! Försök att bevisa
att konstruktionen ger en bisektris.
Geometri - 36
Teori ▪ Skala
Linköpings domkyrka nedan är en bild av den verkliga domkyrkan.
Domkyrkans höjd på bilden är 10,7 cm. Den verkliga domkyrkan är
107 m (=10700 cm) hög. Detta betyder att den verkliga kyrkan är
10700 cm
10,7cm
= 1000 gånger större.
Man säger att bilden är ritad i skalan1:1000. Detta betyder att en sträcka
i bilden motsvaras av en 1000 gånger längre sträcka i det verkliga föremålet.
Bilden är en förminskning av det verkliga föremålet.
Geometri - 37
En bild av en fästing måste förstoras för att alla
detaljer ska framgå tydligt. Om bilden är sådan
att alla längder på den är 30 gånger större än
motsvarande längder i verkligheten säger man
att skalan är 30:1
B
mellan sträckor i bilden
V
1
(=B ) och motsvarande sträckor i verkligheten ( =V ) är
. Alltså är
1000
bilden en förminskning. På motsvarande sätt betyder skrivsättet 30:1
B 30
att förhållandet  . Den bilden är en förstoring.
V
1
Skrivsättet 1:1000 betyder att förhållandet
G6.5
Vad är störst, bilden eller det avbildade föremålet om skalan är
a)1:6 b)1:10 000 c) 5:1 d) 4:5?
G6.6
Eva och Johan skall flytta in i en lägenhet. De vill provmöblera
genom att på en ritning av lägenheten i skalan 1:40 placera
skalenliga bilder av sina möbler.
Vilka mått har bilden av matbordet? Det verkliga bordet är en
rektangel med längden 190 cm och bredden 90 cm.
Vilken radie skall bilden av ett runt bord ha som i verkligheten
har en radie på 70 cm?
De upptäcker att det bara får plats en säng på ritningen av
sovrummet. Den är 5 cm lång och 4 cm bred. Hur stor får den
riktiga sängen då vara?
a)
b)
c)
Geometri - 38
G6.7
Kartan nedan visar Odysseus irrfärder. Hur lång färdades
Odysseus från Troja till sin hemö Ithaka? Kartan är gjord i
skalan 1:15 000 000.
G6.8
Hur högt är det gotiska fönstret från Linköpings domkyrka i
verkligheten (bild s.37)
G6.9
Vid en orienteringstävling var avstånden mellan kontrollerna
på en karta i skalan 1:15000, 7,0 cm, 3,1 cm, 3,7 cm, 4,0 cm,
3,0 cm, 2,2 cm, 3,2 cm och 3,0 cm. Hur lång var orienteringsrundan?
Geometri - 39
Teori ▪ Likformighet
Polygonen B 1 ovan har vi fått genom att polygonen V1 förstorats i
skalan 3:1. Detta innebär att alla de fem sidorna i polygonen B 1 har
blivit 3 gånger längre. Trots förstoringen har de fem vinklarna A, B, C,
D och E i polygonen inte ändrat storlek. Man säger att de två polygonerna är likformiga. Triangeln B 2 är likformig med triangeln V2 och
cirkeln B 3 är likformig med cirkeln V3 ty de har ”samma form”.
Man talar om motsvarande sidor i likformiga trianglar. Man ser ganska
enkelt vad som är motsvarande sidor. Motsvarande sidor står mittemot
lika stora vinklar. Triangeln B har vinklarna A, B och C liksom triangeln
V. Alltså är t ex sidorna b 2 och v 2 motsvarande sidor.
Sidorna i triangeln B är 9 cm, 6 cm respektive 4,5 cm och motsvarande
sidor i triangeln V 2 är 3 cm, 2 cm och 1,5 cm. Kvoterna av motsvarande
sidors längder blir 9cm/3cm, 6cm/2cm och 4,5cm/1,5cm vilket i alla tre
fallen blir 3.
Följande påståenden är användbara vid likformighetsberäkningar:
a) Förhållandet mellan motsvarande sidor i två likformiga figurer är
alltid lika.
b) Två trianglar är likformiga om och endast om de har lika stora
vinklar.
Geometri - 40
Modell ▪ Likformighetsberäkningar
Triangeln Bilden är likformig
med triangeln Verkligheten.
Sidorna i triangeln B är 3 cm, 4
cm och 5 cm. Motsvarande sida
till 3 cm - sidan i triangeln B är
9 cm - sidan i triangeln V.
Bestäm V:s övriga sidor.
Figur B
Figur V
3
9
x
4
y
5
Lösning Trianglarna är likformiga.
Þ
Kvoterna
3
4
och
har
9
x
3 4
=
Þ 3x = 36 Þ x =12
9 x
Vi kan också utnyttja det faktum att förhållandet mellan två sidor i den
ena figuren och förhållandet mellan motsvarande sidor i den andra
5 y
Þ 3y = 45 Þ y =15.
figuren är lika. Vi får =
3 9
samma värde.
Þ
G6.10 Vilka av följande påståenden är sanna?
(a) Om figuren F är likformig med figuren G och G är likformig
med figuren H så är även F likformig med H.
(b) Om vinklarna är lika stora i två femhörningar så är dessa
likformiga.
(c) Två cirkelsektorer är alltid likformiga.
(d) Cirklar är alltid likformiga.
(e) Rätvinkliga trianglar är likformiga.
(f) Liksidiga trianglar är likformiga.
(g) Rektanglar är alltid likformiga.
(h) Likbenta trianglar är likformiga.
Geometri - 41
G6.11 Fatima har hittat på en fiffig metod att beräkna en flaggstångs
höjd. Hon mäter hur lång flaggstångens skugga är samtidigt
som hon mäter hur lång skuggan av en lodrät, rak pinne är.
Pinnen är 1 m lång. Hur hög är flaggstången om flaggstångens
skugga är 10,5 m och pinnens skugga är 0,95 m?
V6.12 Beräkna de obekanta sidorna i de två trianglarna.
V6.13 En remsa med konstant bredd viks. Överlappningen är en
triangel ABC. Vilka egenskaper har denna triangel? Kan du
bevisa det du kommit fram till?
V6.14 Två cirklar har radierna 3 cm respektive 12 cm. Beräkna med
huvudräkning förhållandet mellan cirklarnas omkretsar.
V6.15
Om man klipper ett A4-papper mitt itu, så får man två A5papper. Är dessa två ark likformiga med det ursprungliga A4pappret? Ett A4-ark är 210 mm × 297 mm.
V6.16
I en rätvinklig triangel ABC har ritats mittpunktsnormalen till
hypotenusan BC. Denna linje skär den rätvinkliga triangeln i
punkterna D och E. Hur lång är sträckan DE, om den minsta
kateten är 6,54 cm och hypotenusan är 12,76 cm?
V6.17 Man vill rita rektanglar med arean A cm2, där det naturliga talet
A kan delas upp i exakt 5 primfaktorer, inklusive faktorn 1.
Hur många rektanglar kan man rita, om sidorna är hela
centimeter?
V6.18 Bisektrisen till vinkeln A i triangeln ABC träffar motstående
sida i punkten D. Visa bisektrissatsen, dvs att
AB BD
.
=
AC CD
V6.19 En median delar en triangel i två deltrianglar. Hur förhåller sig
deltrianglarnas areor till varandra?
Geometri - 42
Teori ▪ Periferi- och medelpunktsvinkel
Figurerna nedan visar randvinklar, α, och medelpunktsvinklar, γ, uppritade på samma cirkelbåge b. Medelpunktsvinkeln är alltid dubbelt så
stor som periferivinkeln vilket man upptäcker när man mäter randvinkeln och medelpunktsvinkeln i samma figur. (Prova gärna detta i
något dynamiskt geometriskt program, t ex gratisprogrammet GeoGebra .)
Sats Medelpunktsvinkeln på en cirkelbåge är dubbelt så stor som
randvinkeln på samma båge.
Bevis för fall 1 Låt oss först se på specialfallet att både periferi- och
medelpunktsvinkeln har ett vinkelben liggande på samma diameter.
Vinklarna α och β är lika stora, eftersom de står mot lika långa sidor.
Alltså är γ = α + β men α = β. Då måste γ = 2α.
Bevis för fall 2 Om inte både rand- och medelpunktsvinkeln har ett
vinkelben liggande på samma diameter, så drar vi en diameter som
hjälplinje.
Þ
γ 1 = α1 + β 1 och γ 2 = α2 + β 2 . α1 och β 1 står mot lika långa sidor
och är därmed lika långa. Samma gäller för α2 och β 2
Þ
γ 1 = 2α1 och γ 2 = 2α 2
Þ
γ 1 + γ 2 = 2(α 1 + α 2 ).
Þ
γ 1 + γ 2 = 2α 1 + 2α 2 Þ


medelpunktsvinkel periferivinkel V.S.B.
Fall 3 Försök gärna själv att visa den sista varianten av satsen.
Varför är periferivinklar på samma båge lika stora?
Geometri - 43
G6.20 Bestäm de obekanta vinklarna x och y.
Fundera på detta!
En regelbunden femhörning ABCDE är inskriven i en
cirkel. Beräkna vinklarna i triangeln ABD.
Geometri - 44
Teori ▪ Topptriangelsatsen och transversalsatsen
Topptriangelsatsen
En parallelltransversal i en triangel
bildar en topptriangel i triangeln.
Topptriangeln är likformig med hela
triangeln.
Bevis Sträckan ED är parallell med AC
Þ Vinklarna α = ε och γ = δ ty dessa är
likbelägna vinklar Þ ΔEBD har lika
stora vinklar som ΔABC Þ
Trianglarna är likformiga.
Transversalsatsen
En parallelltransversal delar två sidor i samma förhållande
Bevis Eftersom triangeln EBD är likformig med ABC gäller
b
d
b
d
=
−=
1
−1
……..(1) Û
a +b c + d
a +b
c +d
b
a +b
d
c +d
−
=
−
Û
a +b a +b c + d c + d
b − ( a + b ) d − (c + d )
=
Û
a +b
c +d
b − ( a + b ) d − (c + d )
=
Û
a +b
c +d
−a
−c
=
Û
……..(2)
a +b c + d
Om vi nu dividerar ekvation (1) med (2), får vi
b d
a b
a c

= . V.S.B
=
Û
Û
Û
a c
c d
b d
Geometri - 45
Modell ▪ Topptriangelsatsen och transversalsatsen
Exempel Beräkna sidorna med längderna DE cm och BE cm där sidan
med längden DE är en parallelltransversal. I figuren ovan är a=3,09;
b=4,6 och AC= 9,89
4,6
DE
Lösning Enligt topptriangelsatsen är
som har
=
4,6 + 3,09 9,89
9,89 ⋅ 4,6
lösningen
=
DE = 5,92 . Enligt parallelltransversalsatsen är
4,6 + 3,09
4,6
BE
3,38 ⋅ 4,6
som medför
=
=
BE = 5,05
3,09 3,38
3,09
De sökta sidorna har längderna 5,05 cm respektive 5,92 cm
G6.21 Beräkna längderna av de sträckor som betecknats x och y.
V6.22 Beräkna de
obekanta
längderna x
och y i figuren
bredvid.
Geometri - 46
V6.23
Visa att
ΔADE är
likformig
med ΔCBE.
Använd
likformigheten för att
bevisa att
a∙b = c∙d.
Denna sats
kallas
kordasatsen.
V6.24
Ett rep fästs i vattenbrynet i Vätterns sydspets och dras till
nordspetsen där det fästs på lika sätt och spänns så hårt att det
blir absolut rätlinjigt. På grund av jordytans krökning kommer
repet att gå under vattenytan. Hur djupt nere i sjön ligger repet
på det djupaste stället? Vätterns största längd är 135 km.
Jorddiametern är 12700 km. Bortse från att Visingsö ligger i
vägen för repet.
Geometri - 47
Modell ▪ Konstruktioner - Skärningspunkter mellan en
triangels medianer, bisektriser, mittpunktsnormaler och
höjder. In- och omskrivna cirklar. (endast kurs 2c)
Tre räta linjer går inte genom en gemensam punkt i allmänhet, men det
kan inträffa. (I modulen Vektorer visar vi t ex att en triangels medianer
skär varandra i en gemensam punkt, likaså för höjderna.) Visa med t ex
GeoGebra eller något annat digitalt hjälpmedel att detta gäller för
medianer, höjder, bisektriser och mittpunktsnormaler.
Ledning: Konstruktion av en mittpunktsnormal.
Vilken av de fyra skärningspunkterna (dvs för medianer, höjder,
mittpunktsnormaler och bisektriser) ger en inskriven cirkel respektive en
omskriven?
Geometri - 48
Sats: Om och endast om m är mittpunktsnormal till en korda så går
denna normal genom cirkelns medelpunkt.
Bevis Linjen m är mittpunktsnormal till sträckan CD. Û Alla punkter
på m ligger lika långt från punkterna C och D. Û Cirkelns medelpunkt
ligger på m. V.S.B
G6.25 Rita en cirkel som går genom tre godtyckliga punkter i planet.
Du kan utnyttja figuren ovan (eller använda ett dynamiskt
program).
G6.26 Figuren visar hur du
konstruerar en
tangent EB till en
cirkel, c. Konstruktionen bygger på att
vinkeln mellan
tangenten och
radien, AE, till
tangeringspunkten
E är 90º. Beskriv
hur konstruktionen
utförts. Hur många
tangenter kan man
dra från punkten B
till cirkeln c?
Geometri - 49
V6.27
Det finns ett stort antal geometriska satser tillhörande den
klassiska geometrin. Det kan vara intressant att studera dessa i
ett dynamiskt program.
Geometri-50 Cevians hypotes
Geometri-50 Morleys sats
Geometri-50 Napoleons sats
)XQGHUDSnGHWWD
)RUPXOHUDHQK\SRWHVI|UWYnVNlUDQGH
FLUNODURFKWYnWUDQVYHUVDOHU
Geometri-50 Vinkeln mellan en tangent och en från
tangeringspunkten dragen korda
Geometri - 50
Teori ▪ Area- och volymskala
Areaskalan är kvadraten på längdskalan.
Bevis Antag att vi har två likformiga figurer, t ex två trianglar, T 1 och
T 2 . Av detta följer, att längderna av trianglarnas baser respektive höjder
står i samma förhållande till varandra. Låt detta förhållande vara 1: S. Vi
säger att längdskalan är 1: S. Detta innebär att om basen i triangeln T 1 är
b längdenheter och höjden h längdenheter, så har basen i triangeln T 2
längden b⋅S längdenheter och höjden har längden h⋅S längdenheter.
bh
b⋅S ⋅h⋅S
bh 2
Arean av triangeln T 1 =
och av triangeln T 2 =
=
S .
2
2
2
Alltså är areaskalan lika med kvadraten på längdskalan för triangeln.
Detta gäller inte bara för trianglar utan för alla likformiga plana figurer.
Volymskalan är kuben på längdskalan.
Bevis Antag att vi har två likformiga kroppar, t ex två rätblock, R1 och
R2 . Vi antar att båda dessa kroppars sidor förhåller sig till varandra i
skalan 1: S. Detta innebär att om längden av sidorna i rätblocket R1 är
b, d och h längdenheter så har sidorna i rätblocket R2 längderna b⋅S, d⋅S
och h⋅S längdenheter. Detta innebär att volymen av R1 = b⋅d⋅h och
volymen av R2 = b⋅S⋅d⋅S⋅h⋅S = b⋅d⋅h⋅S 3.
Alltså är volymskalan lika med kuben på längdskalan för rätblocket.
Detta gäller för alla likformiga tredimensionella figurer.
Geometri - 51
Modell ▪ Area- och volymskalan
Exempel Det lilla
prismat är en likformig bild av det stora i
längdskalan 1:5. Hur
stor är arean i det
mindre prismat som
motsvarar arean
59,44 cm2 i det större
prismat? Hur lång är
sidan som motsvarar
9,51 cm i det mindre
prismat?
Lösning Låt A vara arean av det lilla prismat. Eftersom areaskalan är
A
1
kvadraten på längdskalan får vi ekvationen 2 =
59,44
5
59,44
A = 2 vilket medför A = 2,38.
5
Antag att sidan i det mindre prismat är d.
d
1
Likformighetsreglerna ger
= vilket medför d = 1,90.
9 ,51 5
Det mindre prismats area är 2,38 cm2.
Det mindre prismats sida är 1,90 cm
V6.30 En liksidig triangel T 1 är likformig med triangeln T 2 . T 1 :s sidor
är dubbelt så långa som T 2 :s. Hur många trianglar T 2 ryms i
T1?
V6.31 En polygons area är 13,41 dm2 och dess förminskning 7,54 dm2.
En sida i den mindre polygonen är 2,24 dm. Hur lång är motsvarande sida i den större?
Geometri - 52
V6.32 Två koner är likformiga. Den enas radie är 3 gånger större än
den andras radie. Hur många gånger större är den större
konens volym än den mindres?
V6.33 Två pyramider med kvadratiska baser är likformiga. Pyramid B
har basarean 4 dm2 och volymen 12 dm3. Vilken volym har
pyramid V om dess basarea är 9 dm2?
V6.34 Beräkna vinklarna x och y.
G6.35 De två prismorna har två sidor som förhåller sig till varandra
som 10:8. Vilket är förhållandet mellan deras bottenareor och
deras volymer?
Geometri - 53
Facit
1.1 (a), (b), (d), (e), (f), (k)
3.1 Den spetsiga vinkeln är 85°
3.3a) 90°
b) 180°
c) 45°
3.2 a) 120°
b) 60°
3.4a) 90°
b) 180°
c) 45°
d) 22,5°
3.5 Antag att den minsta vinkeln är x°.
x + 2x + 4x + 8x + 16x = 360 Û 31x = 360 Den minsta vinkeln är 11,6°.
3.6 Vid parallella linjer är vinklarna α + β = 180º. (Se figur på s.15). Kalla den till α
likbelägna vinkeln för α 1 . Detta innebär att α 1 + β = 180º. Alltså är α = α 1 enligt
axiom 1 och 3
3.7 Eftersom bisektriser delar vinklar mitt itu blir vinklarna vid bisektris b 1 u/2 och
vid bisektris b 2 v/2. Alltså blir vinkeln mellan bisektriserna u/2 + v/2 = (u + v)/2
3.8 44 º
3.11 Antag att den minsta vinkeln är x°. Þ (x + 11) + (31 + x) + x =180 Û
Û 3x + 42 = 180 Û 3x = 138 Û x = 46 De tre vinklarna är 57°, 77° och 46°.
3.12 Det finns två alternativ:
Alternativ 1: Två vinklar är (x° - 30°) och den tredje är x°.
2(x – 30) + x = 180 Þ 2x – 60 + x = 180 Þ 3x = 240 Þ x = 80
Vinklarna är 50°, 50° och 80°.
Alternativ 2 En vinkel är (x° - 30°) och de två övriga är x°.
x – 30 + 2x = 180 Þ 3x = 210 Þ x = 70 Vinklarna är 40°, 70° och 70°.
3.13
Antag att de två lika stora vinklarna är x°. vilket ger x + 4x + 4x = 180
vilket ger 9x = 180 Alltså x = 20 De tre vinklarna är 20°, 80° och 80°.
3.14 Antag att vinklarna är 3x°, 4x° och 5x° Þ 12x = 180 Þ x = 15
Vinklarna är 45°, 60° och 75°.
3.15 Antag att vinklarna A och B är x°. Yttervinkelsatsen ger 2x = 130
Alltså är vinklarna i triangeln 65°, 65° och 50°.
3.16
Eftersom vinklarna är 90°, 45° och 45° blir yttervinklarna 135°, 135° och 90°.
3.17
Antag att vinklarna inne i figuren längs hypotenusan är x° och y°.
Alltså är 63 + x + 45 = 180
x = 72 Alltså är vinkeln y = 180° – 72° = 108°.
3.18
Om två vinklar i triangeln, α och β, är trubbiga, så är α > 90° och β > 90°.
Alltså är α + β > 180° vilket är omöjligt, eftersom alla tre vinklarna är 180°.
Geometri - 54
3.19 Om triangelns vinklar är α, β och γ så är yttervinklarna (α + β), (α + γ) och
(β + γ). Sålunda är summan av yttervinklarna (α + β) + (α + γ) + (β + γ) = 2(α + β + γ)=
= 360°.
3.20 I triangel finns det två vinklar som är α, eftersom de står mot lika stora sidor.
Alltså är yttervinkeln till dessa två 2α. Även vinkeln vid C är 2α. Varför? Eftersom
vinkelsumman i en triangel är 180°, så är den resterande vinkeln i ∆ABC (180 - 4α).
Eftersom vinklarna efter en rät linje är 180° får vi: α + (180 - 4α) + β = 180 Þ
Þ 3α + β = 0 Þ β = 3α V.S.B.
4.1 Eftersom 2402 + 4182 =
482 kan jag vara nöjd om syftet var ett rektangulärt
rum. Hypotenusan blev bara 1 cm för lång eller 2 promille.
4.2 Avståndet mellan markeringarna är hypotenusan. Alltså är denna sträcka
1, 52 + 22 =
2, 5 . Avståndet mellan markeringarna skall vara 2,5 m.
4.3 I en rätvinklig triangel är ena kateten 7 cm längre än den andra. Hur långa är
kateterna om hypotenusan är 13 cm? Antag att kateterna är x cm och (x+7) cm.
Pythagoras sats ger x2 + (x + 7)2 = 132 vilket ger x2 + x2 +14x + 49 = 169
2x2 + 14x – 120 = 0 vilket ger x2 + 7x – 60 = 0
Prövning med heltal ger x = 5. Kateterna är 5 och 12 cm långa.
4.4 Antalet pixels är 800x600 = 480000 = 4,8⋅105 st.
Skärmens horisontella sida förhåller sig till den vertikala som 800:600 eller förenklat
4:3. Antag att skärmens sidor är 4x och 3x.
Pythagoras sats ger (4x)2 + (3x) 2 = (12,1⋅2,54) 2 Þ 16x2 + 9x 2 = 944,6
Þ x = 6,147
Skärmens sidor är 24,6 (= 4⋅6,147) och 18,4 (=3⋅6,147) cm långa.
4.5 Antag att kateternas längder är 5x och 12x cm. Alltså hypotenusan 120 – 5x –12x
(= 120 – 17x). Pythagoras sats ger (5x)2 + (12x)2 = (120 – 17x)2 Þ
Þ 25x2 + 144x2 = 14400 – 4080x +289x2
120x2 – 4080x + 14400 = 0 Þ x2 – 34x + 120 = 0 Prövning med heltal ger x = 4
Tores rektangel skall ha måtten 20 cm, 48 cm och 52 cm.
Geometri - 55
4.6 Pythagoras sats ger (R + 117) 2 = L2 + R2 Þ R2 + 234R + 1172 = L2 + R2
Eftersom termen 1172 är liten i jämförelse med övriga termer får vi:
234 ⋅ 638 ⋅10000 = 39 000 m = 39 km
1
V4.7 Den övre delen av hypotenusan har längden l.e. Hela hypotenusan fås med
2
234∙R = L2
L=
Pythagoras sats. Den blir
1 2
5
1 +   l .e . =
l .e . och sträckan
2
2
 5 1
5 −1
−  l .e . = l .e . Den sökta kvoten blir då
AP = AQ = 
2
 2 2
(
(
)(
)(
)
)
5 −1 ⋅ 3 + 5
1
5 −1
2 + 2 5 1+ 5
=
=
=
=
, V.S.B.
5 −1 3 − 5
4
2
3− 5 ⋅ 3+ 5
1−
2
Förlängningen med nämnarens konjugatuttryck ( 3 + 5 ) medför att nämnaren blir ett
5 −1
⋅
2
rationellt tal (enligt konjugatregeln). Punkten P säges dela sträckan AB i gyllene snittet.
V4.8 Antag att trädgårdens andra sida är x m. Alltså är diagonalen 60 + x – 20 = 40 + x
Pythagoras sats ger 602 + x 2 = (40 + x )2 vilket medför 602 + x 2 = 1600 + 80 x + x 2
80x = 2000 Alltså x = 25 Trädgårdens andra sida är 25 m
5.1a) c = 23/cos 37° = 25 och a = 23⋅tan 37° = 17
b) a = 23⋅sin 74° = 22 och b = 23⋅cos 74° = 6,3
c) c = 23/sin 13° = 102 och b = 23/tan 13° = 100
5.2 Vinkeln x = 22,5°. Alltså är cos 22,5° = 8/hypotenusan, vilket medför att
hypotenusan = 8,66 cm.
5.3 Halva likbenta triangeln är en rätvinklig triangel med en vinkel på 15,9° och närliggande katet 7 cm. Alltså är de lika långa sidorna hypotenusor. Alltså cos 15,9° =
=7/hypotenusan, vilket medför att de lika långa sidorna är 7,3 cm vardera .
5.4a) tan α = 15/23 vilket medför α = 33°. Alltså är β = 57°.
b) sin α = 7/23 vilket medför α = 18°. Alltså är β = 72°.
c) cos α = 11/23 vilket medför α = 61°. Alltså är β = 29°.
5.5 tan α = 1/3 vilket medför α = 18°. Alltså är β = 72°.
5.6 cos α = 8/8,25 Þ α = 14,1°. Triangelns övriga vinklar 14,1° och 151,8°.
Geometri - 56
5.7
3,22
3,22
= tan 30° vilket medför x = 5,8 vidare är = tan 45° vilket medför y = 3,2
y
x
Alltså är sträckan AB = 9,0 cm.
5.8 cosα = 11/15 ger α=43º
70
5.9 Antag att det är x m till fyren.= tan 3,5° vilket medför att x = 1100 m
x
Skeppet befinner sig 1,1 km från fyren.
5.10 Om strålarna inte kommer till golvet vid sommarsolståndet så sker det aldrig.
21,65
Antag att strålarna når x m ner vid sommarsolståndet. tan19° =
Þ x = 63
x
Enligt beräkningarna når strålarna golvet eftersom det inre rummets höjd är 43 m.
G6.1 Rotation: O Spegling: I, H, M, T, U, V, X, Y, Å, Ä och Ö
G6.2 Enligt Pythagoras sats translateras bordet (82 + 32)0,5 = 8,5 l.e.
G6.4 Hypotes1 : Bisektriserna skär varandra i en punkt
Hypotes2 : Bisektrisernas skärningspunkt är medelpunkt för den inskrivna cirkel
Bevis Hjälplinjer ger kongruenta trianglar …….
G6.5a) Verkligheten
b) Verkligheten
G6.6a) 4,75 cm x 2,25 cm
c) Bilden
b) 1,75 cm
d) Verkligheten
c) 200 cm x 160 cm
G6.7 Kartan ger en resa på »390 mm. Detta innebär en resa på 590 mil
G6.8 c:a 12 m
G6.9 7,0 cm + 2,1 cm + 2,7 cm + 3,0 cm + 3,0 cm + 1,2 cm + 2,2 cm + 2,0 cm =
23,2 cm Alltså är orienteringsrundan 23,2⋅15000 cm = 3,48 km
G6.10 Påståenden (a), (d) och (f) är sanna.
G6.11 Antag att flaggstången är x m hög. Likformighet ger ekvationen:
x 10,5
=
som
1 0,95
ger x = 11 Flaggstångens höjd är 11 m.
V6.12 Antag att sträckan 43 m delas i x m och (43 – x) m. Likformighet ger
x
43 − x
=
. Utan nämnare får vi ekvationen 8,7x = 5,2(43 – x)
5,2
8,7
som förenklas till 8,7x = 223,6 – 5,2x. Alltså 13,9x = 223,6 med lösningen x = 16,1
Geometri - 57
Antag nu att hypotenusorna är y respektive z l.e.
Pythagoras sats ger ekvationerna:
y2 = 5,22 + 16,12
z2 = 8,72 + (43-16,1)2 Lösningarna är y = 17 och z = 28
De båda trianglarnas obekanta sidor är 16 och 17 respektive 27 och 28 l.e.
V6.13 Triangeln är likbent eftersom vinklarna vid B och C är likbelägna innan
remsan viks.
V6.14 1:4
V6.15 Sidorna till ett A5-papper är alltså 210 och 297/2 mm.
Alltså blir förhållandet mellan sidorna för A5 210 / (297/2) = 1,414.
Förhållandet mellan sidorna för A4 är 297/210 = 1,414.
Ett A5-ark är likformigt med ett A4-ark.
V6.16
Kateten BC är 10,96 cm enligt Pythagoras sats. Sträckan DC = 12,76/2 = 6,38 cm
Antag att sträckan DE är x cm. Eftersom triangeln CDE är likformig med CBA får vi
x
6,54
=
som ger x = 3,81. Sträckan DE är 3,81 cm lång.
6,38 10,96
V6.17 A = 1abcd.Man kan rita trianglar med sidorna: (1, abcd), (a, bcd), (b, acd),
(c, abd), (d, abc), (ab, cd), (ac, bd), (ad, bc) och (bc, ad) dvs 9 stycken.
V6.18 Dra en linje genom C parallell med AB. Denna linje skär bisektrisen till vinkeln
A i punkten E. Trianglarna BDA och CDE är likvinkliga och alltså likformiga.
Triangeln CAE är likbent, alltså är CA = CE. Likformigheten ger att
AB BD
=
.
AC CD
V6.19 Antag att medianen träffar sidan a. Höjden (= h) mot denna sida träffar
vinkelspetsen A. De båda deltrianglarna har samma bas a /2 och höjd h. Alltså
förhåller sig deras areor till varandra som 1:1.
G6.20a) x = 50° b) x = 25,5° c) x = 106° d) x = y = 90° e) x = y = 32°
f) y = 54,5° och x = 62° g) x= 75,5° och y = 104,5° h) x = 135° i) x = 49° & y = 26°
G6.21a) Topptriangelsatsen ger
x
3,62
=
som ger x = 3,80.
5,95 (3,62 + 2,05)
Geometri - 58
b) Topptriangelsatsen ger
x
3, 42
=
som ger
( x + 2, 41) 5,14
5,14x = 3,42x + 8,2422 Û 1,72x = 8,2422 Û x = 4,79 (l.e.)
Transversalsatsen ger
y
4,79
=
som ger y = 5,53 (l.e.) .
2, 41 2,78
V6.22
x
3,78
=
som ger x = 3,16.
2,35 2,81
y
3,04
=
Enligt transversalsatsen är
som ger y = 2,54.
2,35 + 3,16 3,78 + 2,81
Enligt transversalsatsen är
V6.23
Triangeln EDA är likformig med EBC eftersom randvinklarna EDA och EBC samt
EAD och ECB är lika.
a d
Alltså gäller =
som medför ab = cd. V.S.B.
c b
V6.24 Använd kordasatsen som säger att om två kordor skär varandra i en cirkel är
produkten av den ena kordans delar lika med produkten av den andra kordans delar.
Den ena kordans delar är båda 135/2 km och den andra kordans delar är x km och
(12700 − x) km. Ekvationen blir, men eftersom x är mycket mindre än 12700 kan det
2
2
135 
135 
x (12700 − x ) eller 
försummas, det vill säga =

 = x ⋅12700 .
 2 
 2 
Ekvationen har lösningen x = 0,359. Repet ligger alltså på 359 m djup.
V6.30
4 st
V6.31 Areaskalan =
13, 41
= 1,78 . Detta innebär att längdskalan är 1,78 .
7,54
Alltså är motsvarande sida i den större polygonen 2,24 1, 78 = 3,0 dm.
V6.32 33 = 27
V6.33 Eftersom basareorna förhåller sig som 4:9 så måste motsvarande sträckor
förhålla sig som 2:3. Detta medför att volymerna förhåller sig som 23:33, dvs 8:27.
27 ⋅12
Detta innebär att den större pyramidens volym är
dm3 = 40,5 dm3
8
V6.34 Medelpunktsvinkeln till 65 gradersvinkeln är 2⋅65° = 130°. Alltså är 360° 130° (= 230°) medelpunktsvinkel till x. Detta medför att x = 115°.
Alltså är 115° +93° + 65° + y = 360° vilket medför y = 87°
V6.35 Bottenareorna förhåller sig till varandra som 100:64 och volymerna 1000:512
Geometri - 59
Geometri - 60