helsingin seudun biotekniikan koulutusohjelma valintakoe
advertisement

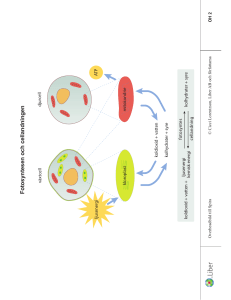
1 HELSINGFORSREGIONENS UTBILDNINGSPROGRAM I BIOTEKNIK URVALSPROVET 25.5.2009 Efternamn___________________________ Förnamn____________________________ Personbeteckning_____________________ BIOLOGI (20 p) 1a. Assimilationen (fotosyntesen) och de faktorer som påverkar den.(10 p) 1b. Vart och i vilka molekyler hamnar koldioxiden slutligen? (4 p) 1c. Vad händer då en växt innesluts i en tät kammare på en ljus plats och den ges märkt koldioxid? Vart hamnar kolet, vad händer? Vad händer om växten hålls i mörker? (4 p) Tydlighet och logik (2 p) Modellsvar: 1 a. Vad är assimilation: Vid assimilationen tillverkas socker av vatten och koldioxid med hjälp av solens ljusenergi. Solens ljusenergi binds till kemisk energi (ATP). Samtidigt frigörs syre. (2 p) Vilka assimilerar: växter, alger, flagellater, vissa bakterier (1 p) Var sker assimilationen, reaktionsekvationen: Assimilationen sker i kloroplasterna, där det finns klorofyll (1 p). Flest kloroplaster finns det i assimilationsvävnaden (0,5 p) . Kloroplastens struktur (0,5 p) 6 H2O+6CO2 ----> C6H12O6 + 6O2 (1 p) I ljusreaktionen bryts vattenmolekylerna med hjälp av ljusenergi ner till väte och syre, som försvinner via klyvöppningarna. I mörkerreaktionen förenas vätet med koldioxiden med hjälp av enzymer och energi och glukos bildas. (2 p) Vad inverkar: Mängden ljus, temperaturen, mängden koldioxid, fukten, näringsämnena, luftföroreningarna (2 p) 1b. Till vad används assimilationsprodukterna: till byggnadsmaterial eller energi (1 p) Vad görs av glukosen: sackaros, stärkelse, cellulosa, olja, aminosyror, proteiner (3 p) 1c. I en ljus och tät kammare fungerar växtens ljusreaktion och mängden syre i kammaren ökar (1 p). På motsvarande sätt minskar kammarens mängd koldioxid, då den binds till byggnadsmaterial eller energi för växten. (1 p). Det märkta kolet hamnar i de föreningar som nämns vid punkt 1b. (1 p). I mörker finns inte solens ljusenergi, vilket leder till att assimilationens energikälla fattas. Ingen assimilation sker. (1 p). 2 HELSINGFORSREGIONENS UTBILDNINGSPROGRAM I BIOTEKNIK URVALSPROVET 25.5.2009 Efternamn___________________________ Förnamn____________________________ Personbeteckning_____________________ MATEMATIK (20 p) Vi undersöker en mikrobpopulations storlek som en funktion av tiden. Vid tidpunkten noll är populationens storlek obetydlig, och den betraktas såsom som noll. I inledningsfasen, speciellt i goda förhållanden, är populationens ökning kraftig och då växer funktionen som beskriver populationen snabbt. Senare, då maten sinar (åtminstone i proportion till populationens storlek), blir tillväxten långsammare och närmar sig slutligen den övre gränsen R, som beskriver miljöns bärkraft. Den typ av tillväxt som presenteras ovan kan beskrivas med (åtminstone) två funktioner, Michaelis-Menten-funktionen och med en modifierad version av en viss exponentfunktion: Michaelis-Menten: M(t) = R[t / (b + t)] Exponenten: E(t) = R[1 - exp(-bt)] där t står för tid, R är en gemensam parameter för båda funktionerna (se på punkt a) och b den parameter som definierar funktionens form (formparameter; som inte nödvändigtvis har samma värde i dessa två funktioner); exp är exponentfunktionen exp(x) = ex. Skriv ditt svar på uppgiftspappret i tomrummet efter frågorna. Uppgifterna: a) Vilket är gränsvärdet för funktionerna M och E, när t ? När t är båda funktionernas gränsvärde R. För funktionen M fås gränsvärdet då man förkortar med faktorn t, och för funktionen E fås gränsvärdet med exponentfunktionens egenskaper. I det senare fallet måste man dessutom anta att b > 0. (3 p) 3 HELSINGFORSREGIONENS UTBILDNINGSPROGRAM I BIOTEKNIK URVALSPROVET 25.5.2009 Efternamn___________________________ Förnamn____________________________ Personbeteckning_____________________ MATEMATIK (20 p) b) Ge en tolkning av parametern R på basis av punkten a. Båda funktionerna R har en övre gräns som populationens storlek närmar sig. Som det redan sades i introduktionen är R det största möjliga värdet (”miljöns bärförmåga”) populationen kan få. H (3 p) c1) Vid vilken tidpunkt (vi använder beteckningen Mt50 för den) uppnår funktionen M värdet R/2 ? Funktionen M(t) = R/2 lösning är t = b. (2 p) 4 HELSINGFORSREGIONENS UTBILDNINGSPROGRAM I BIOTEKNIK URVALSPROVET 25.5.2009 Efternamn___________________________ Förnamn____________________________ Personbeteckning_____________________ MATEMATIK (20 p) c2) Vid vilken tidpunkt (vi använder Et50 för den) uppnår funktionen E värdet R/2 ? Funktionen E(t) = R/2 Går att hyfsa till formen exp(-bt) = ½. Genom att ta den naturliga logaritmen för båda leden får man -bt = -ln(2), där t = ln(2)/b (2 p) 5 HELSINGFORSREGIONENS UTBILDNINGSPROGRAM I BIOTEKNIK URVALSPROVET 25.5.2009 Efternamn___________________________ Förnamn____________________________ Personbeteckning_____________________ MATEMATIK (20 p) d) Vilket värde ska funktionen E:s formparameter b ha (som en funktion av funktionen M:s formparameter) för att värdena Mt50 och Et50 ska vara samma? Låt funktionen M:s formparameter vara bM och funktionen E:s motsvarande bE. (Redan märkningen av formparametrarna så här ger 4 p. Om man inte skiljer på formparametrarna kan man inte lösa uppgiften.) Genom att använda c1 och c2- punkternas resultat får vi funktionen bM = ln(2) / bE, där bE = ln(2) / bM, (6 p) e) Vid vilken tidpunkt tMAX växer funktionerna M och E snabbast? Funktionen växer snabbast när dess derivata är som störst. Eftersom båda funktionernas derivatas derivata alltid är negativ (t > 0), minskar tillväxthastigheten när t växer. Den största tillväxthastigheten för båda funktionerna fås när t = 0. (4 p)