Linnéuniversitetet
advertisement

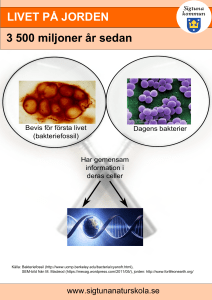
Linnéuniversitetet Matematik Hans Frisk Diskreta Dynamiska System, del II 1. IFS-ormbunke. Precis som i förra bilden så tar man en punkt i planet och låter den hoppa runt och efter ett litet tag så ligger man nära ett objekt som ser ut som en ormbunke! 105 punkter är plottade här. För att förstå detta behöver man först förstå de geometriska transformationerna som krävs. De transformationer som inte ändrar objektets utseende kallas kongruensavbildingar och är förflyttningar (translationer), rotationer och speglingar. Sedan kan man behålla formen men förminska eller förstora, det är likformighetsavbildningarna. Till sist finns töjningar och, eller, kompressioner i en led samt skjuvningar då en kvadrat avbildas på en parallellogram. Alla dessa tillsammans kallas för af f ina transf ormationer och man kan visa att två godtyckligt valda trianglar i planet kan avbildas på varandra om alla sådana transformationer är tillåtna. Hur gör man dessa avbildningar matematiskt? Jo man använder matriser där determinanten är skild från noll. För ormbunken används faktiskt 4 sådana transformationer. En av dem ser ut så här xn+1 = 0.85xn + 0.04yn , yn+1 = −0.04xn + 0.85yn + 1.6 Denna transformation kan ses som en en rotation, följt av en förminskning och till sist en förflyttning uppåt. För att beskriva ett sådant komplext objekt som en ormbunke behöver man verka med 4 affina transformationer [1]. Ett praktiskt sätt att generera ormbunken är att vid varje iteration slumpmässigt välja en av de fyra transformationerna. Den som anges i formeln ovan används i 85 procent av iterationerna. Ja det är mycket att fundera över här och vill du läsa mer så är [2] en mycket fin introduktion till geometri och fraktaler. IFS står för iterated function systems och ett roligt exempel på sådant är följande: Välj en punkt inne i en liksidig triangel och numrera hörnen 1,2 och 3. Kasta en tärning blir det 1 eller 2 så går du halvägs mot hörn 1, 3-4 halvägs mot hörn 2 och visar tärningen 5 eller 6 så gå du halvvägs mot hörn. Så kastar du tärningen igen och upprepar proceduren från den nya punkten. Frågor: 1) Gör kaosleken (chaos game) för den liksidiga triangeln som beskrivs ovan. Mät inte för noga med linjalen för då tar det för lång tid. Vilket mönster blir det om man håller på tillräckligt länge? 2) Om alla punkter i en kvadrat med hörn i (0,0), (0,1), (1,1) och (1,0) avbildas en gång med avbildningen ovan, hur har kvadraten deformerats? Linjer avbildas på linjer. 2. Lindenmayer-buske. Mer från växtriket! Biologen Aristid Lindenmayer (1925-1989) utvecklade ett slags språk för att beskriva celldelning och sedan också hur växter förgrenar sig. Koden för busken nedan är F → F [+F ]F [−F ][F ] (1) F står här helt enkelt för ett vertikalt linjesegement med en fix längd. Plus (minus) betyder en utväxt 20 grader åt vänster (höger) och hakparentesen att vi skall gå tillbaks till där utskottet började. En eller två iterartioner klar vi väl men sedan får datorn ta över. Växten nedan har itererats 5 gånger och består av 55 = 3125 sidor. Man utgår alltså från en vertikal sida och varje F skall ändras enligt regeln ovan. Andra regler ger andra växter, se kapitel 1 i [3]. Frågor: 1) Rita växten efter en iteration. 2) Om regeln ändras till F → F [+F ]F [−F ]F, diskutera hur den nya växten skiljer sig från den gamla. (2) 3. Drakkurvan. Här ett annat Lindenmayer-system som ser ut som en kinesisk drake. Två sorts sidor denna gången, L och R kallar vi dom och de har samma fixa längd. Regeln är L → L + R+, R → −L − R De viktiga här är att hålla rätt på plus- och minustecknen. Plus betyder vänstersväng 90 grader i färdriktningen och minus högersväng 90 grader. Vi startar med en L sida och sedan upprepar vi reglerna ovan på varje L och R. Så vår bäbis drake får 2, sedan 4, 8 , 16 sidor och så vidare. Dyker det upp strängar som ++- så skall det som en vänstersväng. Bilden visar en tonårsdrake med 217 sidor. Är det en fraktal? Ja men inte av den enkla typen man först möter som Cantor mängden och Kochs snöflingekurva. Överhuvudtaget har det visat sig svårt att hitta en bra definition av vad en fraktal är. Delarna skall på något sätt vara lika med helheten. Se [2] för en precisering av denna idé. Frågor: 1) Starta med en L sida och rita drakkurvan efter 3 iterationer. 4. Cellular Automata, regel 746. Cellular Automata (CA) är ett annat försök att hitta matematik för biologiska system. Ta ett rutat A4 papper och fyll några rutor med svart. De står för liv och de vita rutorna för icke-liv. För att räkna ut vad som skall hända i nästa generation så behövs en regel. För den CA som visas i figuren gäller födsel, vit till svart, om den vita cellen har precis tre svarta celler i grannskapet. Med grannskapet menar vi här de 8 celler som ligger närmast den vita cellen. Överlevnad, svart till svart, om det finns högst 4 levande celler i grannskapet. Död, svart till vit, inträffar vid överbefolkning, alltså fem till åtta levande grannar. Observera att alla celler uppdateras samtidigt i varje generation. I Mathematica finns ett kommando inbyggt för att beräkna framtiden för våra levande celler. Regelen ovan kan kodas och tillskrivas ett regelnummer, i detta fall 746. Regeln skall tala om vad som händer då mittcelllen är svart eller vit och antalet levande grannar är noll till åtta så antalet regler är 218 = 262144. För figuren så startade jag med 3 lodräta levande celler följt av en död och sedan på toppen en levande cell. Så en upp-ner asymmetri är inbyggd från början. Sedan itererades denna CA 3000 gånger och resultatet är ett nästan cirkulärt objekt med en liten topp högst upp. Förstorar man upp det inre av det cirkulära området kommer man urskilja de vita och svarta och vita cellerna. De svarta är i klar majoritet men små öar med vita celler finns här och var. Tidigare trodde man att detta var en CA för cirkulär tillväxt men så upptäckte man denna spets däruppe som börjar bildas efter cirka 2700 iterationer. Vad lär vi oss av detta? Kanske att bli lite mer ödmjuka inför naturens komplexitet. Mycket är svårt eller omöjligt att förutsäga som t.ex. Belinmurens fall, att homo sapiens blev jordbrukare eller att regel 746 börjar utveckla en spets efter 2700 generationer. En mycket läsvärd introduktion till CA är [4] som är en recension av Steven Wolframs mastodontverk A New Kind of Science [5]. Frågor: 1) Ta ett rutat A4 och starta med ett frö som består av en lodrät följd av tre levande, en död och sedan en levande igen. Itererar 2 gånger enligt regeln i texten, F-3 grannar, Ö ≤ 4 grannar, D ≥ 5 grannar. 2) Vad händer med vårt frö då regeln ändras till F-3 grannar, Ö 2-3 grannar, D 0-1 eller 4-8 grannar. Här dör en cell både av ensamhet och överbefolkning. Detta är den mest berömda CA som studerats och den kallas Game of Life. 5. Fångens dilemma. Tänk dig att du bor i storstad och funderar på om du skall ta bilen eller åka kollektivt till jobbet. Om alla andra åker kollektivt så tjänar du mycket tid genom att ta bilen. Problemet är bara det att om många fler tänker så kommer du att sitta fast i ändlösa bilköer och det kommer ta längre tid än att åka kollektivt. Vi har ett dilemma och detta är ett sätt presentera det som brukar kallas fångens dilemma. Ett centralt problem inom evolutionsläran sedan Darwins dagar är varför vi väljer att samarbeta och uppträda osjälviskt. För att försöka förstå detta så har olika slags spel undersökts. I exemplet som figuren visar kan varje cell befinna sig i två tillstånd, precis som regel 746 ovan. Men nu kallar vi dem C, individer som alltid samarbetar (åker kollektivt), och D för de som inte vill samarbeta (tar bilen). Vi startar med en D i mitten av ett 99×99 rutnät och övriga celler befolkas av C. I varje generation tävlar man med sina 8 närmsta grannar och sig själv och den som får högst poäng tar över mittcellen. Två C får 1 poäng vardera, en D mot en C ger 1.9 poäng till D medasn C får noll poäng. Bilden som ser ut som en persisk matta visar läget efter 200 iterationer. Röd markerar D territorium som också var det iterationen innan och på samma sätt markerar blå relativt stabilt C område. Striden står just nu vid grönt, har precis gått från C till D, och vid gult (övergång från D till C). Kom ihåg att vi startade med endast en D men de har alltså förökat sig. För mer detaljer se [6]. Stort tack till Björn Lindenberg som skrivit Mathematica koden. Frågor: 1) Tag ett rutat A4 och sätt ett D i mitten och resten C. Hur ser det ut efter en iteration? Man tävlar med alla sina grannar och poängen addreras. Den av de nio som får högst poäng äger mittrutan i nästa iteration. 2) Vad händer då 1.9 ändras till 1.1 eller 3? Referenser [1] Michael F. Barnsley, Fractals Everywhere, Academic Press, 1993. [2] Judith N. Cederberg, A Course In Modern Geometries, Springer, 2010. [3] Przemyslaw Prusinkiewicz och Aristid Lindenmayer, The Algoritmic Beauty Of Plants, Springer 1996. Finns att ladda ner på http://algorithmicbotany.org/. [4] http://www.ams.org/journals/notices/200302/fea–gray.pdf [5] Steven Wolfram, A New Kind Of Science, http://www.wolframscience.com/nksonline/toc.html [6] Robert May, Bull.of the AMS,32,No 3,1995. Se http://www.ams.org/journals/bull/1995–32 –03/home.html