Trigonometri

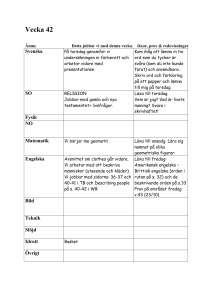
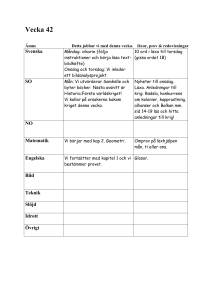
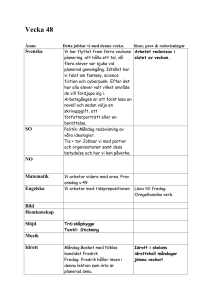
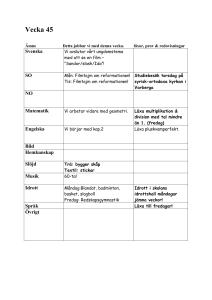
Sidor i boken
26-34
Trigonometri
Definition: Gren av matematiken som studerar samband mellan vinklar och sträckor i planet (och
rymden).
Det grundläggande trigonometriska problemet är att beräkna alla sidor och vinklar i en triangel när
vissa av dessa är kända. Det handlar då om plan trigonometri.
Här ska vi hålla oss till rätvinkliga trianglar. I senare kurser kommer trigonometrin att innefatta
godtyckliga trianglar. Ibland kommer det trots allt att dyka upp icke rätvinkliga trianglar. Då är
lösningen, att med hjälp av en konstruktion, till exempel genom att dra en höjd åstadkomma två
rätvinkliga trianglar.
Närliggande och Motstående står i relation till vinkeln v, som är given eller efterfrågad.
tan v =
motstående katet
närliggande katet
tan v =
a
b
sin v =
motstående katet
hypotenusan
sin v =
a
c
cos v =
närliggande katet
hypotenusan
cos v =
b
c
Innan vi sätter igång att solvera rätvinkliga trianglar ska du se till att din räknare är inställd på
”räkning i grader”. Kontrollera att 45 TAN ger resultatet 1. Vinklar mäts i allmänhet i grader
(360◦ på ett varv) eller i radianer (2π på ett varv). Här ska vi hålla oss till grader.
Håkan Strömberg
1
KTH STH
Känner man två storheter i formlerna ovan, kan man enkelt bestämma den tredje.
Nr
Känt Sökt
I
v, a
b
II
v, b
a
III
a, b
v
IV
v, a
c
V
v, c
a
VI
a, c
v
VII
v, b
c
VIII
v, c
b
IX
b, c
v
Formel
a
b=
tan v
a = b · tan v
v = arctan a
b
a
c=
sin v
a = c · sin v
v = arcsin ac
b
c=
cos v
b = c · cos v
v = arccos bc
I formlerna III, VI och IX ska man bestämma en vinkel. till exempel
v = arcsin
1
≈ 19.47
3
På dosan trycker man då SIN−1 1/3 ≈ 19.47 och motsvarande COS−1 för arccos och TAN−1
för arctan.
Problem 1. Vad kallas triangeln i figuren. Bestäm h och b.
Lösning: En triangel med vinklarna 30◦ − 60◦ − 90◦ kallas en halv liksidig.
h = 20 sin 60◦ ≈ 17.32
b = 20 cos 60◦ = 10
Den korta kateten är då häften så lång som hypotenusan. Antag att hypotenusan är 2a, sidan b = a.
Med hjälp av Pythagoras sats kan vi så räkna ut sidan h
(2a)2
4a2
3a2
h
h
=
=
=
=
=
a2 + h2
a2 + h2
h2
√
3a2
√
a 3
√
Av detta får vi att höjden i en liksidig triangel med sidan 2a är h = a 3.
Håkan Strömberg
2
KTH STH
Problem 2. Beräkna triangelns area.
Lösning: Med hjälp av formeln
A=
b·h
2
Först bestämmer vi höjden genom AD = h
h = 46 · sin 41◦ ≈ 30.18
sedan BD = b1
b1 = 46 · cos 41◦ ≈ 34.72
och så DC = b2
b2 ≈
30.18
≈ 20.36
tan 56◦
Till sist kan vi bestämma arean
A=
(20.36 + 34.72) · 30.18
≈ 831.11
2
Svar: 831 cm2
Problem 3. Beräkna den rätvinkliga triangelns area.
Lösning: Basen BC = 50. Höjden mot BC = h får vi genom
h = 39 · sin 40◦ ≈ 25.07
Arean blir då
A=
25.07 · 50
≈ 626.72
2
Vi kunde likväl bestämt oss för att beräkna höjden mot AB = h, som ger
h = 50 · sin 40◦ ≈ 32.14
Arean blir då
39 · 32.14
≈ 626.72
2
Samma resultat! Hur överraskande var det?
A=
Längre fram i era matematikstudier (närmare bestämt nästa kurs), kommer ni att stifta bekantskap
med areasatsen, som efter denna uppgift är lätt att inse
A=
Håkan Strömberg
a · b · sin γ
2
3
KTH STH
där γ är vinkeln mellan a och b.
Problem 4. I en likbent triangel är höjden hälften av basens längd. Arean är 400 cm2 . Bestäm
triangelns omkrets.
Lösning: Antag att höjden är AD = x. Då är basen BC = 2x. Vi kan då teckna en ekvation med
hjälp av formeln b·h
2 .
x · 2x
= 400
2 2
2x = 800
x2 = 400
√
x =
400
x = 20
Höjden är alltså AD = 20 och basen BC = 40. Återstår att bestämma längden hos de två lika långa
benen AB och AC. Höjden delar basen mitt itu i en likbent triangel. Med hjälp av Pythagoras sats
kan vi nu bestämma AC = y i △ADC.
y2
y
y
= √
202 + 202
2√· 202
=
= 20 2
√
Triangeln ADC är en √
halv kvadrat. Vi finner att diagonalen idenna kvadrat, AC är
√ 20 2. Det vill
säga kvadratens sida · 2. Så är det alltid. Bra att veta. Vi får omkretsen 40 + 2 · 20 2 ≈ 96.57 cm.
Svar: 96.6 cm
Problem 5. Beräkna figurens omkrets
Lösning: AD = x kan vi få fram direkt genom
sin 49◦ =
34
x
som ger x = AD ≈ 45.05 Vi kan också bestämma ED = y med hjälp av
tan 49◦ =
34
y
som ger y = ED ≈ 29.56. Turen har nu kommit till BE = z. Vi får
tan 53◦ =
Håkan Strömberg
4
z
34
KTH STH
som ger z = BE ≈ 45.12. Vi vet nu att BD = 29.56 + 45.12 = 74.68. Nu kan vi gå på △BCD. Först
BC = u. Vi får
74.68
cos 24◦ =
u
som ger u ≈ 81.75. I nästa steg bestämmer vi DC = v genom
v
tan 24◦ =
74.68
med resultatet v = DC ≈ 33.25. Återstår så AB = w. Vi får
34
cos 53◦ =
w
som ger w =≈ 56.50
Nu kan vi bestämma omkretsen
45.05 + 56.50 + 33.25 + 81.75 = 216.55
Svar: Omkretsen är 217 cm
Nedan följer först 9 uppgifter, alla med rätvinkliga trianglar och med en obekant. Ibland efterfrågas
sidan x och ibland vinkeln v. Tillsammans kommer de 9 olika situationerna från tabellen ovan att
tillämpas exakt en gång!
Läxa 1.
Bestäm v
Läxa 2.
Bestäm x
Läxa 3.
Bestäm x
Håkan Strömberg
5
KTH STH
Läxa 4.
Bestäm v
Läxa 5.
Bestäm x
Läxa 6.
Bestäm v
Läxa 7.
Bestäm x
Läxa 8.
Bestäm x
Håkan Strömberg
6
KTH STH
Läxa 9.
Bestäm x
Läxa 10.
Bestäm rektangelns omkrets
Läxa 11.
Bestäm figurens omkrets
Läxa 12. Givet △ABC där sidan BC är dubbelt så lång som sidan AC. Höjden CD = 63 cm mot
sidan AB och ∠BAC = 44◦ . Bestäm triangelns area.
Läxa Lösning 1. Formel III
v = arctan
5
≈ 29◦
9
Läxa Lösning 2. Formel V
x = 11.4 · sin 38◦ ≈ 7
Läxa Lösning 3. Formel I
x=
5
≈ 6.9
tan 36◦
Läxa Lösning 4. Formel IX
v = arccos
6
≈ 39.7◦
7.8
Läxa Lösning 5. Formel VII
v=
Håkan Strömberg
7
≈ 8.6
cos 36◦
7
KTH STH
Läxa Lösning 6. Formel VI
v = arcsin
6
≈ 36.9
10
Läxa Lösning 7. Formel VIII
Läxa Lösning 8. Formel II
Läxa Lösning 9. Formel IV
x = 9.2 cos 40◦ ≈ 7
x = 7 · tan 45◦ ≈ 7
9
≈ 11.41
sin 52◦
Läxa Lösning 10. Vi bestämmer höjden h och basen b genom
x=
b = 60 cos 30◦ ≈ 51.96
och
h = 60 sin 30◦ ≈ 30
Omkretsen blir då
2h + 2b ≡ 2 · 51.96 + 2 · 30 ≈ 163.92
Observera att höjden ska man kunna se direkt eftersom diagonalen delar rektangeln i två ’halva
liksidingar’
Svar: 164 cm.
Läxa Lösning 11. För att kunna bestämma
△BCD. Pythagoras sats ger
x2
x
x
AB och AD behöver vi BD. BD = x är hypotenusa i
32 + 42
√
25
5
=
=
=
△BCD är ofta förkommande, eftersom alla sidor är heltal, och kallas för den egyptiska triangeln. När
vi betraktar △ABD ser vi att den är en halv kvadrat eftersom den har vinklarna 45◦ − 45◦ − 90◦ .
Det betyder att AB = BD = 5. Återstår så att bestämma AD = y. Vi kan använda trigonometri eller
Pythagoras sats, vilket som.
sin 45◦ = y5
y = sin 545◦
y ≈ 7.07
√
Det är√ bra att känna till att för en given sida s i en kvadrat är diagonalen s 2. I vår uppgift
y = 5 2 ≈ 7.07.
Vi får så omkretsen
3 + 4 + 5 + 7.07 = 19.07
Svar: 19 cm
Läxa Lösning 12. Du måste rita figur! Antag att CA = x och CD = 2x. Med hjälp av
sin 44◦ =
63
x
får vi x = CA ≈ 90.69. Vi vet nu att CB = 2x ≈ 181.38. Vi beräknar nu AD = y
tan 44◦ =
63
y
ger y = AD ≈ 65.24. Sedan över till DB = z som vi får genom Pythagoras sats
2
2
181.382 = 63
√ +z
z =
181.382 − 632
z ≈ 170.09
Håkan Strömberg
8
KTH STH
Nu har vi basen AB = 65.24 + 170.09 = 235.33 och kan därmed bestämma arean
A=
63 · 235.33
≈ 7412.84
2
Svar: 7413 cm2
Håkan Strömberg
9
KTH STH
Tuff vecka
• Trigonometri
– Föreläsning 14. Uppgifter: Läxa 1-11.
– Föreläsning 15: Uppgifter: Läxa 1-8.
– Boken sid 26 − 36. a och b uppgifter.
• Räta linjen
– Föreläsning 16. Uppgifter: Läxa 1-15.
– Föreläsning 17: Uppgifter: Läxa 1-15.
– Boken sid 142 − 147. a och b uppgifter.
• Linjära ekvationssystem
– Föreläsning 19. Uppgifter: Läxa 1-14.
– Boken sid 142 − 147. a och b uppgifter.
– Kursbunten sid 5 − 12.
• Repetition
– Kursbunten 22-25, Area och Volymskala
• Repetition Föreläsning 18
I KS2 ingår
• Potenser
• Rötter
• Likformighet
• Trigonometri
• Räta linjen
• Linjära ekvationssystem
Det är rimligt att förvänta sig 2 poäng inom varje område.
Håkan Strömberg
1
KTH STH