Polarisation laboration Vågor och optik
advertisement

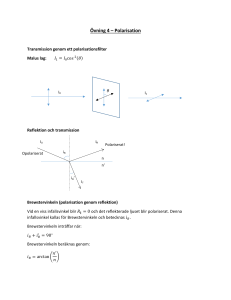
(Sensur) Polarisation laboration Vågor och optik Utförs av: William Sjöström 19940404-6956 (Sensur) Philip Sandell 19950512-3456 Laborationsrapport skriven av: William Sjöström 19940404-6956 (Sensur) Sammanfattning I laborationen undersöks hur bra polaroidfilter följer Malus lag, resultatet är att det inte finns några filter som följer Malus lag till 100%, men att det är en bra approximation vid teoretiska beräkningar. Även Fresnels reflektions-ekvationer och Brewstervinkeln undersöks. Uppsala 2015-12-04 1 (av 9) Inledning En ljusvåg är alltid linjärt polariserad när den emitteras men det naturliga ljuset som upplevs vid jordens yta består av många olika ljusvågor från olika källor, alla polariserade men i slumpvisa riktningar. Ibland kan detta leda till olägenheter, exempelvis när ljus reflekteras så kan ögat bli bländat, detta kan lösas med polariserade solglaslgon. I andra fall kan man utnyttja olika polarisationsriktningar för nöjets skulle, exempelvis för att skapa en 3D-film. Slumpmässigt polariserat ljus kan polariseras till linjärt polariserat ljus antingen genom att passera ett polaroidfilter som enbart släpper igenom en av ljusets E-fältsriktningar. Eller genom att reflekteras med en infallsvinkel som kallas för Brewstervinkeln, då svänger dipolerna i reflektionsytan parallellt med den reflekterade strålen. Laboration delas upp i två delar, experiment 1 och experiment 2. I experiment 1 undersöks hur mycket ljus som transmitteras genom två polaroider när vinkeln mellan deras polariseringsaxlar varieras. Här undersöks även hurvida de polariationsfilter som finns är ideala, det vill säga följer Malus lag eller inte. I experiment 2 undersöks vad som händer med ljus när det reflekteras. En glasskivas brytningsindex bestäms genom att experimentellt bestämma Brewstervinkeln. Sedan undersöks hur bra Fresnels reflektions-ekvationer beskriver en ljusvåg som reflekteras. Teori Malus Lag[1] Figur 6. Illustrerar Malus lag. Malus lag beskriver hur ett idealt polariseringsfilter släpper igenom polariserade ljusstrålar, figur 6: (1) Där I är ljusintensiteten efter filtret, I0 ljusintensiteten innan filtret och θ är vinkeln mellan det infallande ljusets polarisationsaxel och filtrets polaristionsaxel. 2 (av 9) Snells lag[2] Figur 7. Illustrerar Snells lag. Snells lag beskriver hur en ljusstråle bryts när den går från ett medium med brytningsindex n1 till ett annat med brytningsindex n2. θ1 är infallsvinkeln mot ytnormalen och θ2 är utgångsvinkeln från ytnormalen, se figur 7. (2) Brewstervinkeln Vid en viss infallsvinkel, Brewstervinkeln, θB, så blir den reflekterade ljusstrålen polariserad (med polarisationsriktning in och ut ur skärmen enligt figur 1). Detta inträffar endast när vinkeln mellan det reflekterade och det transmitterade ljuset är 90:. Figur 1. Beskriver hur formel för Brewstervinkel fås. En formel för Brewstervinkeln kan fås ur Snells lag, se figur 1. Genom att sätta θ3=90:-θB fås: Detta kan skrivas om till: ( ) (3) Eller: (4) Fresnelekvationena[3] Fresnels reflektions-ekvationer beskriver hur E-fältets amplitud förändras vid reflektion: När E-fältet är parallellt med infallsplanet (detta kallas P-polariserat ljus) så är E-fältets reflekterade amplitud: (5) När E-fältet är vinkelrätt mot infallsplanet (detta kallas för S-polarisetat ljus) så är E-fältets reflekterade amplitud: (6) E-fältet kvadrerat är analogt med ljusets intensitet, detta används vid plottningen av resultatet i experiment 2. 3 (av 9) Metod Laborationerna utfördes i mörker för att fotodioden skulle utsättas för så lite bakgrundsstrålning som möjligt. Materialet som användes: Lampa (slumpmässigt polariserat ljus). Irisbländare (skärmar av perferin). Lins (fokuserar ljuset). Två polaroidfilter. Fotodiod (ger en spänning när den träffas av ljus). Multimeter. Experiment 1 Figur 2. Visar hur utrustningen monterades vid den första delen av laborationen. (1) glödlampa, (2) irisbländare, (3) lins, (4) och (5) roterbara polaroidfilter, (6) fotodiod kopplad till en multimeter (7). Experimenten utfördes enligt följande: 1. Utrustningen monterades enligt figur 2, lampan tändes och irisbländaren justerades till en stor öppning (cirka 2cm i diameter). 2. Det andra polaroidfiltret, (5) i figur 2, togs temporärt bort. I2 mättes (värdet som multimetern visade noterades). Det andra polaroidfiltret monterades tillbaka. 3. De två polaroidfiltren, (4) och (5) i figur 2 justerades så att de hade samma polarisationsvinkel. 4. Den andra polaroiden, (5) i figur 2, roterades 10: och värdet på multimetern noterades. 5. Steg 4 upprepades tills de två polaroidfiltren hade samma polarisationsvinkel igen (dvs 180: från ursprungsläget). 4 (av 9) Experiment 2 Figur 3. Visar hur utrustningen monterades i andra delen av laborationen. (1) glödlampa, (2) irisbländare, (3) lins, (4) roterbart polaroidfilter, (5)en glasskiva monterad på en roterande axel tillsammans med (6) fotodiod kopplad till en multimeter (7). Experimentet utfördes enligt följande för P-polariserat ljus: 1. Utrustningen monterades enligt figur 3, lampan tändes och irisbländaren justerades till en liten öppning (cirka 0,7cm i diameter). 2. Glasskivan, (5) i figur 3, justerades så att det transmitterade ljuset från ploarisatorn, (4), reflekterades till fotodioden, (6), även när (5) och (6) roterades runt rotationsaxeln. 3. Polarisationsfiltret, (4), roterades så att polaroidaxeln var horisontell enligt figur 3 (Ppolarisation). 4. (5) och (6) roterades 10: runt rotationsaxeln så att ljuset reflekterades i (5), I3 noterades. 5. Steg 4 upprepades 7 gånger (till 80: från läget som figur 3 visar). 6. Sedan gjordes extra mätningar vid 25:, 35: och 45:. Experimentet utfördes enligt följande för S-polariserat ljus: 1. Utrustningen monterades enligt figur 3, lampan tändes och irisbländaren justerades till en liten öppning (cirka 0,7cm i diameter). 2. Glasskivan, (5) i figur 3, justerades så att det transmitterade ljuset från ploarisatorn, (4), reflekterades till fotodioden, (6), även när (5) och (6) roterades runt rotationsaxeln. 3. Polarisationsfiltret, (4), roterades så att polaroidaxeln var vertikal enligt figur 3 (Spolarisation). 4. (5) och (6) roterades 10: runt rotationsaxeln så att ljuset reflekterades i (5), I3 noterades. 5. Steg 4 upprepades 7 gånger (till 80: från läget som figur 3 visar). 5 (av 9) Resultat Experiment 1 Uppmätta värden och teoretiskt beräknade värden med ekvation (1) redovisas i tabell 1. I figur 4 finns Malus lag plottat tillsammans med de uppmätta mätvärderna från tabell 1. Tabell 1. Mätvärden och teoretiska värden för experiment 1. Vinkel I3/I2 (exp) I3/I2 (teo) 0 0,65 1 10 0,63 0,97 20 0,59 0,88 30 0,51 0,75 40 0,4 0,59 50 0,3 0,41 60 0,18 0,25 70 0,08 0,12 80 0,02 0,03 90 0 0 100 0 0,03 110 0,2 0,12 120 0,9 0,25 130 0,19 0,41 140 0,31 0,59 150 0,42 0,75 160 0,52 0,75 170 0,59 0,88 180 0,64 1 Figur4, Visar mätvärderna från experiment i plottat tillsammans med Malus lag. 6 (av 9) Experiment 2 I tabell 2 finns uppmätta värden och teoretiskt beräknade värden med ekvation (6) kvadrerad för Spolariserat ljus. I tabell 3 finns uppmätta värden och teoretiskt beräknade värden med ekvation (5) för P-polarisation. I figur 5 finns värden från tabell 2 och 3 plottade tillsammans med ekvation (5) och (6) kvadrerade, samtliga värden är dividerade med I2 för att få förhållandet. Tabell 2. Mätvärden och teoretiska värden för experiment 2 med S-polarisation. Vinkel I3/I2 (exp) I3/I2 (teo) 10 0,04 0,05 20 0,04 0,06 30 0,05 0,07 40 0,06 0,09 50 0,1 0,13 60 0,14 0,2 70 0,24 0,33 80 0,38 0,56 Tabell 3. Mätvärden och teoretiska värden för experiment 2 med P-polarisation. Vinkel I3/I2 (exp) I3/I2 (teo) 10 0,37 0,23 20 0,07 0,04 30 0,02 0,01 40 0 0 45 0 0 50 0,01 0,01 55 0,01 0,01 60 0,02 0,02 65 0,05 0,03 70 0,06 0,04 80 0,07 0,05 Tabell 3 visar att Brewstervinkeln är ungefär vid 55-60:, snittet blir alltså 57,5:. Med n1 i ekvation (4) fås: 7 (av 9) Figur 5. Uppmätta värden från tabell 2 och 3 plottade tillsammans med Fresnels reflektionsformler kvadrerade. Diskussion Experiment 1 I figur 4 kan upmärksammas att de experimentella värderna är något förskjutna i x-led i förhållande till den teoretiska kurvan. Detta beror troligen på att polaroidfiltren inte hade sin polaroidaxel i exakt samma riktning när mätningen påbörjades, således blev hela kurvan förskjuten, i detta fall i den positiva x-riktningen. Det kan bero på att att polatoidfiltret inte låg helt rätt mot grad-skalan, eller helt enkelt osäkerheten hos det mänskliga ögat. Från figur 4 kan även uppmärksammas att de experimentella värderna är något mindre än de teoretiska värderna i y-led, det vill säga, de följer inte Malus lag exakt. Detta beror på att polarisatorerna som användes inte är ideala utan släpper igenom några procent av ljusets komponent som är vinkelrät till polaroidaxeln. Således kan det andra polaroidfiltret filtrera bort ytterligare lite av den vinkelräta ljus-komponenten, vilket även förklarar varför I3 är mindre än I2 när polaroidaxlarna är i samma riktning. Experiment 2 I figur 5 kan observeras att Fresnels ekvationer beskriver det reflekterade ljuset med bra säkerhet. Det kan observeras att vissa mätpunkter befinner sig ”ovanför” Fresnels ekvationer, detta beror troligen på bakgrundsstrålning (dvs ljus) i laborationssalen. Det är bara det P-polariserade ljuset som når 0 i intensitet, vilket motsvarar värderna i experiment där två polaroidfilter placeras efter varandra med polariseringsaxlarna roterade 90: från varandra (glasskivan motsvarar alltså det andra polaroidfiltret). Detta bevisar att ljuset vid reflektion i Brewstervinkeln blir polariserat vinkelrätt mot infallsplanet som nämnt i inledningen. Det S-polariserade ljuset motsvarar isället två polaroidfilter efter varandra med polarisationsaxeln i samma riktning. 8 (av 9) Slutsatser Polaroidfilter används främst inom synoptik, det vill säga i glasögon. Som diskuterat i experiment 2 så kommer ljus som infaller med Brewstervinkeln reflekteras som linjärt polariserat ljus. Detta innebär solljuset blir linjärt polarisetat med E-fältet i den horisontella riktningen när det infaller med Brewstervinkeln mot horisontella ytor, till exempel en sjö. Således får E-fältet störst amplitud i den horisontella riktningen, detta orsakar att sjön blänker och en observatör riskerar att bli bändad. Detta kan motverkas genom att använda glasögon som har polariserande glas med polaroidaxeln i den vertikala riktningen (det bländande horisontella ljuset polariseras bort). Därav har ofta dyrare solglasögon polariserande glas. Ett annat bekant fenomen uppstår om man roterar ett av de polariserade glasen med 90:. Det blir då möjligt för det ena ögat att se endast vertikalt polariserat ljus medan det andra endast ser horisontellt polariserat ljus. Detta kan användas för att skapa 3D-filmer. Det uppstår dock problem om man skulle luta huvudet en aning då glasen skulle polarisera ljuset i fel riktningar. För att lösa detta använder man idag ofta cirkulärt polariserande glasögon istället, det vill säga det ena ögat ser medurs polariserat ljus medan det andra ser moturs polariserat ljus. Referenser [1] P.H sid 274 [2] P.H sid 275 [3] P.H sid 272-273 9 (av 9)