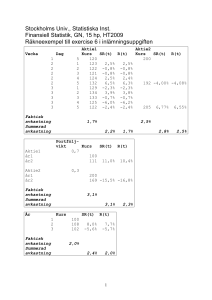
Erik Sjöberg

Innehåll
Förord
1. Makroekonomisk analys
1.1 Grundläggande begrepp
1.2 Penningpolitik och centralbanker
1.3 Finanspolitik
1.4 Stabiliseringspolitik enligt Keynes
1.5 Inflation och arbetslöshet
1.6 Den öppna ekonomin
1.7 Valutapolitik och EMU
1.8 Avkastningskurvan, korta och långa räntor
2. Värdering av finansiella instrument
2.1 Räntebegrepp
2.2 Enkel och effektiv ränta
2.3 Nominell och real ränta
2.4 Nuvärde, slutvärde och annuiteter
2.5 Diskonteringränta
2.6 Värdering av obligationer
2.7 Värdering av aktier
2.8 Värdering av optioner
3. Risk och avkastning
3.1 Lägesmått - Aritmetiskt och geometriskt medelvärde
3.2 Direktavkastning och värdeförändring
3.3 Faktisk och förväntad avkastning och risk
3.4 Riskfri ränta och riskpremie
3.5 Risktyper
3.6 Spridningsmått: varians och standardavvikelse
4. Avkastning och risk i portfölj
4.1 Avkastning i portfölj
4.2 Samvariation (korrelation)
4.3 Risk i portfölj
4.4 Diversifiering
5. Marknadsmodellen, systematisk och specifik risk
5.1 Marknadsmodellen
5.2 Beta m fl. regressionsresultat
5.3 Systematisk och specifik risk
5.4 Diversifiering sett från marknadsmodellen
1
6. Portföljvalsteori
6.1 Effektiva portföljer
6.2 Effektiv front, utan och med riskfri tillgång
6.3 Effekt av belåning
6.4 Capital Asset Pricing Model (CAPM)
6.5 CAPM som värderingsmodell: bara systematisk risk förtjänar en riskpremie
7. Utvärdering av portföljer och fonder
7.1 Riskjusterad avkastning
7.2 Sharpe-kvoten
7.3 Jensens alfa
7.4 Treynorkvot
7.5 Tracking Error och informationskvot
7.6 Relevanta jämförelseindex
7.7 Rating av fonder
8. Privatekonomi: hur välja portfölj i praktiken?
8.1 Sparutrymme (löpande ekonomi)
8.2 Nettoförmögenhet (tillgångar, skulder)
8.3 Placeringshorisont och sparmål
8.4 Analys av kundens riskattityd (risktolerans, riskvilja, riskaversion)
8.5 Empiriska resultat om risk och samvariation för olika fondkategorier
8.6 Fondportföljer för olika risknivåer
8.7 Strategisk och taktisk allokering samt rebalansering
9.0 Avslutning
Ordlista
2
Ekonomi
Förord
Detta kompendium syftar till att ge en grundläggande förståelse för att behärska de
kunskapskrav som ingår i delområde 2 Ekonomi inför SwedSecs licensieringstest för
rådgivare från och med 2014. Det vänder sig också till dig, som vill ha en grundläggande
förståelse inom national- och finansiell ekonomi på värdepappersmarknaden, utan att skriva
SwedSecs test. Tyngdpunkten har lagts på att försöka beskriva beräkningsmetoder och
modeller på ett informellt sätt utan avancerade formler och grekiska bokstäver. Däremot
förekommer rikligt med räkneexempel och empiriska resultat, från vad som faktiskt händer på
kapitalmarknaden, för att du lättare ska förstå. De fetmarkerade orden i texten återfinns i
ordlistan i slutet av kompendiet.
Utdrag ur SwedSecs kunskapskrav:
”Delområde 2 fokuserar på frågan om hur man på bästa sätt väljer värdepappersportföljer
anpassade för olika kunders situation och behov. Detta uppdrag kräver att licenshavaren har god
kunskap om begreppen förväntad avkastning, risk och risktolerans och en detaljerad förståelse
för riskegenskaperna hos portföljer av finansiella tillgångar. Licenshavaren måste också
behärska grunderna i värdering av finansiella instrument, förstå diversifieringens möjligheter och
begränsningar samt kunna analysera kundens privatekonomiska situation och attityd till
risktagande. En viss kunskap om makroekonomiska begrepp, samband och metoder är också
nödvändig för en djupare förståelse för avkastning och risk för olika placeringsalternativ.”
För att klara av SwedSecs test förväntas du kunna göra vissa beräkningar, men framförallt
handlar det om att du ska förstå innebörd och skillnader. Majoriteten av frågorna och
svarsalternativen på SwedSecs test är textbaserad.
1. Makroekonomisk analys
1.1 Grundläggande begrepp
Det som händer i ekonomin i stort har stor betydelse för avkastningen på olika tillgångar på
kapitalmarknaden. I själva verket har förväntningar om ekonomiskt tillväxt och inflation helt
avgörande betydelse för utvecklingen på kapitalmarknaden. Vid studiet av kapitalmarknaden
finns det därför goda skäl att känna till viktiga begrepp inom nationalekonomi.
De viktigaste begreppen inom nationalekonomi är tillväxt och inflation. Tillväxt kan
definieras som förändring i produktionen av varor och tjänster, mätt i fasta priser eller volym.
Produktionen i ett land mäts med måttet bruttonationalprodukt (BNP). Tillväxten i BNP
brukar vanligen beräknas utifrån vad olika varor och tjänster används till (”BNP från
användningssidan”) men kan även mätas utifrån produktion eller inkomster. BNP från
användningssidan sammanfattas ofta i en tabell kallad försörjningsbalansen.
3
Nettot av export minus import samt nettot av kapitalavkastning mot utlandet utgör ett lands
finansiella nettosaldo mot utlandet, vilket brukar kallas för bytesbalans. När det uppstår
kraftiga förändringar i tillväxten i BNP i ett litet exportberoende land som Sverige beror det
ofta på dramatiska förändringar i den internationella ekonomins utveckling, senast
exemplifierad med finanskrisen hösten 2008. Det som hände då, med en negativ förändring av
BNP år 2009 på ca 5 % kan kallas för en efterfrågechock, efterfrågan på svenska exportvaror
dök mycket snabbt.
Det förekommer även s.k. utbudschocker. Exempel på sådana är problem inom
livsmedelsförsörjningen i samband med missväxt, vilket kan leda till kraftiga uppgångar i
livsmedelspriserna.
Den ekonomiska politiken (penning- och finanspolitik) har ofta som mål att ekonomin ska
uppvisa stabil och hög tillväxt. Syftet att stabilisera tillväxten och inflationen kallas ofta för
just stabiliseringspolitik.
Sverige BNP-förändring i procent
8
6
4
2
0
2011
4
2008
Källa: Konjunkturinstitutet
2005
-6
2002
-4
1999
1996
1993
1990
1987
1984
1981
-2
Inflation definieras som uppgång i den allmänna prisnivån och mäts vanligen som förändring i
konsumentprisindex (KPI). Även för inflationen brukar den ekonomiska politiken har mål i
form av låg (men gärna positiv) ökning av konsumentpriserna. Om den genomsnittliga
prisnivån skulle falla kallas det för deflation och det kan innebära en farlig situation, framför
allt då det hämmar investeringar samt innebär att utestående skulder stiger i reala termer.
Sverige inflation i procent (KPI)
14
12
10
8
6
4
2
0
2013
2011
2009
2007
2005
2003
2001
1999
1997
1995
1993
1991
1989
1987
1985
1983
1981
-2
Källa: Konjunkturinstitutet
1.2 Penningpolitik och centralbanker
Den ena delen av den ekonomiska politiken kallas penningpolitik. Ansvarig för denna är i
Sverige Riksbanken, som brukar kallas för världens äldsta, grundad redan år 1668. Som
jämförelse grundades den amerikanska centralbankens Federal Reserve så sent som 1913.
Penningpolitiken kan ha olika mål, ofta sammankopplat med vilken växelkursregim ett land
har. Sverige har sedan november 1992 s.k. rörlig växelkurs, vilket innebär att Riksbanken
låter marknaden bestämma växelkursen mellan SEK och andra valutor. Riksbankens
penningpolitiska mål utgörs istället av det s.k. inflationsmålet. Riksbankens inflationsmål är
att förändringen i konsumentprisindex ska uppgå till 2 procent per år +/- 1 procent, eller med
andra ord ska den ligga mellan 1 och 3 procent per år.
Riksbankens medel för att påverka inflationen går via Riksbankens möjlighet att styra den
korta räntan. Riksbankens styrränta kallas för reporäntan, vilket är den ränta som
Riksbanken använder för att förse banksystemet med likviditet. Ordet repa är en förkortning
av det engelska uttrycket repurchase agreement, som kan översättas med återköpsavtal.
Det kommer av att riksbanken veckovis köper obligationer av bankerna med ett samtidigt
avtal om att de ska köpa tillbaka samma obligationer en vecka senare. I vissa lägen då
bankerna har överskottslikviditet förekommer även s.k. omvända repor, vilket innebär att
riksbanken säljer obligationer till bankerna med avtal om återköp en vecka senare.
5
Under normala omständigheter brukar en förändring av Riksbankens reporänta få ett direkt
genomslag på interbankmarknadens korta räntor. Dessa räntor kallas i Sverige för Stibor,
vilket står för Stockholm Interbank Offered Rate. Stibor är den ränta som bankerna ställer till
varandra för utlåning i svenska kronor. Räntan fastställs varje dag och används ofta i sin tur
som referensränta för andra kontrakt på marknaden. Motsvarigheten till Stibor i andra valutor
är Libor (London Interbank Offered rate) och Euribor (Euro Interbank Offered rate).
Genom det deklarerade inflationsmålet är det lätt att bedöma hur Riksbanken kommer att göra
med reporäntan. Vid tendenser till stigande inflation, t ex. en bedömning att inflationen
framöver kommer att överstiga 3 procent, så kan man räkna med att Riksbanken höjer
reporäntan i syfte att dämpa tillväxten och inflationen i ekonomin. Omvänt gäller att vid en
bedömning att inflationen kan komma att understiga 1 procent så kan man räkna med att
Riksbanken kommer att sänka reporäntan i syfte att stimulera ekonomin och få till något
högre inflation.
Riksbanken har vidare ansvaret för att samordna arbetet med finansiell stabilitet, och i
samband med det publicerar den regelbundet en rapport vid namn Finansiell stabilitet.
Riksbanken är enligt gällande lagstiftning oberoende från bl. a regeringen och styrs av en
direktion bestående av riksbankschefen och fem vice riksbankschefer. De håller
penningpolitiska möten sex gånger per år, där det fattas beslut om styrräntan – reporäntan.
Vid dessa möten förs ett protokoll som offentliggörs några veckor efter mötet. Sedan 2007
offentliggör Riksbanken även sin prognos över hur reporäntan kommer att utvecklas under de
närmaste tre åren, en s.k. räntebana.
Penningpolitiken inom euro-området sköts av ECB, den europeiska centralbanken med säte i
Frankfurt, Tyskland. ECBs penningpolitiska mål är liksom riksbankens ett inflationsmål,
nämligen att inflationen får vara högst 2 procent (jämför svenska Riksbankens 1-3 procent).
ECBs mål har preciserats till under, men nära 2 procent. Det finns dock kvar centralbanker i
de 17 medlemsländerna, som bl. a ansvarar för utgivning av sedlar och mynt i euro för
respektive land. Liksom svenska Riksbanken, beslutar ECBs styrelse om tre policy-räntor: en
styrränta för "main refinancing operation", ibland kallad "refi rate", samt en inlånings- och
utlåningsränta.
Den amerikanska centralbanken, Federal Reserve, har som mål att sträva efter hög
sysselsättning och stabila priser. På längre sikt innebär det att stabilisera inflationen kring ett
mål på 2 procent och att stabilisera arbetslösheten runt en skattad långsiktigt hållbar nivå (den
naturliga arbetslösheten) på cirka 5-6 procent.
1.3 Finanspolitik
Finanspolitiken utgör den andra delen av ekonomiska politiken. Den omfattar beslut om
statens utgifter och inkomster och bedrivs av regering och riksdag. De beslut som riksdagen
kan fatta är t ex vad avser utgifter, ersättningsnivåer i olika försäkringssystem som
arbetslöshets- och sjukförsäkring eller för inkomster, skattesatser avseende olika skatter. Lika
lite som ett hushåll eller ett företag, kan dock staten i förväg bestämma, vilket utfall det
kommer att bli mellan utgifter och inkomster – det som kallas för budgetsaldo. Hur det
verkliga budgetutfallet utvecklas hänger nära ihop med den allmänna utvecklingen i
ekonomin. Vid hög tillväxt ökar statens inkomster, medan utgifterna för t ex.
arbetslöshetsförsäkring minskar, vilket normalt leder till ökande överskott i statens
6
budgetsaldo. Motsatsen gäller vid fallande eller stillastående BNP med växande underskott
som följd.
Statsbudgeten för år 2013 omfattar inkomster på 829,6 mdr kr och utgifter på 837,2 mdr kr,
vilket innebär ett i sammanhanget obetydligt underskott, särskilt jämfört med de flesta andra
utvecklade industriländerna. De största utgiftsposterna är s.k. transfereringar, d.v.s. olika
former av bidrag och försäkringsersättningar. Bland poster som hör till offentlig konsumtion
finns rättsväsendet 39,4 mdr kr, försvar 46,2 mdr kr, hälso- och sjukvård och social omsorg
62,2 mdr kr samt utbildning och forskning 57,1 mdr kr.
En restriktiv finanspolitik kännetecknas bland annat av att man politiskt stramar åt efterfrågan
genom att höja skatter och sänka bidrag.
Under en stor del av efterkrigstiden (1950-1970-talen) förespråkades en aktiv finanspolitik i
syfte att stabilisera tillväxten och undvika lågkonjunkturer. Faran med en sådan aktiv
finanspolitik upptäcktes inte förrän mot slutet av 1970-talet med kraftigt stigande inflation
och omfattande underskott i statsbudgetarna. Sedan 1980-talet har de flesta länderna, så även
Sverige, varit väsentligt mer försiktiga med att använda finanspolitiken i stabiliseringspolitiskt
syfte. I Sverige ansvarar Riksgäldskontoret för finansieringen av statens underskott och
förvaltningen av statsskulden.
1.4 Stabiliseringspolitik enligt Keynes
De klassiska ekonomerna hade en optimistisk syn på de fria marknadskrafterna. Utbud och
efterfrågan korrigerade sig självt genom löne- och prisjusteringar så att man hittade tillbaka
till en långsiktig jämvikt. Det behövdes alltså ingen särskild stabiliseringspolitik för att rätta
till obalanser. Under 1930-talets krisår började man ifrågasätta denna bild eftersom man hade
en så utbredd massarbetslöshet - lönesänkningar skulle inte kunna rädda situationen. Istället
kom alternativa lösningar, framförda av bl.a. den engelske ekonomen John Maynard Keynes.
De hävdade att det fanns en betydande stelhet i hur priser och löner sattes. De koncentrerade
sig också på efterfrågesidan, istället för utbudssidan som de klassiska ekonomerna hade haft
fokus på. Exempelvis så var den Keynesianska synen på lönen, att den utgör en köpkraft för
arbetarna, inte bara en kostnad för företagen.
Även enligt den Keynesianska synen var jämvikt mellan utbud och efterfrågan viktig, men
anpassningen mot jämvikt sker inte genom att priserna justeras (eftersom de är trögrörliga)
utan genom att kvantiteterna sålda och köpta varor förändras. Slutsatsen enligt Keynes var att
man skulle bedriva en aktiv stabiliseringspolitik genom att påverka den aggregerade
efterfrågan. Man skulle stimulera efterfrågan om man hade hög arbetslöshet och strama åt
efterfrågan om man hade för hög inflation.
Man kom också fram till att det fanns en multiplikatoreffekt, en positiv spiral som en
ekonomi kunde komma in i. Det medförde att den ursprungliga stimulansen fick en betydligt
större effekt på slutresultatet, stimulansen multiplicerar sig själv. Enkelt uttryckt är
multiplikatoreffekten, att om man stimulerar efterfrågan så ökar konsumtionen. Då säljer
företagen mer och tjänar mer pengar, så att de kan anställa fler. Om det blir fler anställda är
det fler som får löner och kan börja konsumera. Då tjänar företagen ännu mer pengar och kan
anställa ännu fler, osv.
7
1.5 Inflation och arbetslöshet
Under en högkonjunktur stiger efterfrågetrycket i ekonomin, då sysselsättning och produktion
ökar. Det ökade efterfrågetrycket driver i sin tur upp inflationen. Sambandet mellan inflation
och arbetslöshet beskrivs av den s.k. Phillipskurvan. På kort sikt är detta samband negativt,
dvs. en hög arbetslöshet innebär en låg inflationstakt och vice versa.
Enligt den kortsiktiga Phillipskurvan skulle man alltså kunna nå en lägre arbetslöshet genom
att bedriva en expansiv politik. I diagrammet ovan skulle då arbetslösheten minska från u1 till
u2 till priset av en stigande inflation. Det långsiktiga sambandet mellan inflation och
arbetslöshet påverkas av löntagarnas inflationsförväntningar. Om löntagarna vill ha
löneförhöjningar som kompensation för minskad köpkraft, så förskjuts den kortsiktiga
Phillipskurvan uppåt (se diagrammet nedan). För varje arbetslöshetsnivå ligger då
inflationstakten på en högre nivå än tidigare. När företagen anpassar sig efter den nya
kostnadsnivån, ökar arbetslösheten igen och man är tillbaka på den nivå man startade på, u*.
Det långsiktiga sambandet mellan inflation kan därför illustreras med en lodrät linje, dvs. att
det inte finns något samband mellan inflation och arbetslöshet. Arbetslösheten återgår på sikt
till den långsiktiga naturliga arbetslösheten.
8
Den naturliga arbetslösheten orsakas av att arbetskraftens kompetens inte stämmer överens
med den kompetens som efterfrågas, eller att arbetskraften bor på fel ställe. Det kan bli så
genom att vissa branscher försvinner antingen genom att totala efterfrågan minskar eller
genom att de lokala arbetstillfällena blir utkonkurrerade. Den naturliga arbetslösheten kan
minska genom att öka produktiviteten, satsa på utbildning samt genom åtgärder som gör att
arbetsmarknaden blir mer flexibel.
1.6 Den öppna ekonomin
Med en öppen ekonomi menas ett land som har utrikeshandel, dvs. som exporterar och
importerar varor och tjänster, till och från andra länder och kapital kan röra sig fritt. Det
påverkar sysselsättning, inkomstfördelning och möjligheterna att bedriva ekonomisk politik.
Speciellt gäller det för ett litet land som Sverige med en stor utrikeshandel. Bytesbalansen är
ett mått på hur mycket som produceras i ett land jämfört med resursanvändningen. Ett
underskott innebär att vi lever över våra tillgångar, och mellanskillnaden måste täckas med
utlandsupplåning. Det leder till en ökad utlandsskuld och ett ökat beroende av de
kreditgivande ländernas välvilja.
Ett mål med den ekonomiska politiken är därför att Sverige ska ha en extern balans, dvs. att
underskott i bytesbalansen vissa år motverkas av överskott andra år. Det låter väl bra, men det
gör det samtidigt svårare att bedriva en expansiv politik, där man stimulerar hushållen till
ökad konsumtion. En del av den ökade konsumtionen går nämligen till importerade varor,
vilket ökar importen och försämrar bytesbalansen. Samtidigt gynnas inte vår export av
stimulanspolitiken, eftersom exporten av våra varor beror på våra grannländers
konsumtionsvilja, så där får vi ingen hjälp. Det som ytterligare kan förvärra situationen är att
den ökade inhemska efterfrågan driver upp den inhemska inflationen, vilket gör våra varor
mindre attraktiva för våra grannländer, med minskad export som följd. En stimulativ politik
leder alltså till ökad konsumtion, vilket man vill, men det kan också leda till ökad import och
minskad export. Det är därmed en målkonflikt mellan den inre och yttre balansen.
De egenskaper som en öppen ekonomi har, kan även motverka de gynnsamma effekterna av
penningpolitiken. Om Riksbanken vill kyla av ekonomin för att bromsa inflationen, så höjer
de styrräntan. Högre räntor minskar konsumtionen, vilket man vill, men det kan även leda till
9
två andra effekter som är mindre bra. Den höjda räntan gör det mer intressant för utländska
investerare att placera på den svenska räntemarknaden, vilket skapar ett inflöde av valuta och
den svenska valutan stärks. Valutainflödet leder till att likviditeten i ekonomin ökar och driver
på konsumtionen. Den starkare valutan gör vår import billigare och exporten blir dyrare, med
försämrad bytesbalans som följd.
Liknande problematiska bieffekter finns om Riksbanken istället vill stimulera tillväxten
genom att sänka räntorna. Sänkta räntor leder till ett utflöde av kapital och försvagad valuta.
Den försvagade valutakursen är bra i det här fallet, eftersom det gör vår export mer attraktiv,
vilket stimulerar vår exportindustri. Däremot minskar likviditeten genom utflödet av kapital
och det kan dämpa konsumtionen.
Så kan effekterna bli om landet har en rörlig växelkurs, vilket Sverige har. Med en rörlig
växelkurs (kallas ibland för flytande växelkurs) menas att valutamarknaden fritt bestämmer
värdet på valutan utifrån utbud och efterfrågan. Med en fast växelkurs menas att
centralbanken bestämmer vad valutakursen ska vara.
Nu lite terminologi som kan vara bra att ha med sig. Om ett lands valuta stärks så kallas det
att valutan apprecierar vid rörlig växelkursregim, medan det kallas att valutan revalveras
vid en fast valutaregim. Om ett lands valuta istället försvagas kallas det att valutan
deprecierar respektive devalveras.
1.7 Valutapolitik och EMU
Som nämndes tidigare tillämpar Sverige sedan november 1992 s.k. rörlig växelkurs.
Dessförinnan hade Sverige fast växelkurs, vilket innebar att Riksbanken bestämde en nivå
för kursen mellan SEK och en viss valuta eller en korg av flera andra valutor. En sådan politik
tillämpas idag fortfarande av t ex. Danmark, som knutit kursen på DKK mot EUR, vilket även
är fallet i baltiska stater som Lettland och Litauen.
Ett ännu mer radikalt valutasamarbete är att använda en gemensam valuta, vilket är fallet för
EUR, där för närvarande 17 olika länder inom EU har infört den gemensamma valutan. Detta
har skett inom EUs samarbete EMU, som är en förkortnings för Economic and Monetary
Union. Även Sverige deltar i EMU och är i princip bundet att - om inträdeskraven är
uppfyllda – övergå till EUR.
Det finns ett antal inträdeskrav för att kunna gå över till euro. Det är krav på högst 60%
statsskuld/BNP, högst 3% budgetunderskott/BNP, inflation som inte får vara för hög samt att
valutan ska ha varit relativt stabil mot euron under senaste två åren. Även efter att ett land
anslutit sig, ska kraven avseende statsskuld och budget vara uppfyllda enligt den ursprungliga
s.k. stabilitetspakten, annars skulle landet få erlägga böter. Euron började dock inte så bra när
i tur och ordning Frankrike och Tyskland bröt mot dessa krav redan 2001-2 och vägrade
betala böter. Efter den processen tycks inget euro-land känt något särskilt tryck på att hålla
budget och skuld i skick.
Ett av EUs senaste projekt för att hantera den europeiska statsskuldkrisen är en ny variant av
den gamla stabilitetspakten, en finanspolitisk pakt som skulle ge EU-kommissionen visst
inflytande över ländernas budgetarbete. Frågan är om det kommer att finnas någon respekt för
gemensamma EU-regler denna gång, när man så flagrant har nonchalerat sådana tidigare.
10
Andra viktiga internationella organisationer är IMF, OECD och BIS. IMF, Internationella
Valutafonden baserad i Washington DC, USA, har ca 200 medlemsländer och är den
institution som har till uppgift att stödja länder med betalningsproblem. Under senare år har
länder som Island, Lettland, Ukraina, Grekland, Portugal och Irland fått lån från IMF. OECD,
Organisation for economic cooperation and development, baserad i Paris, är en
samarbetsorganisation för utvecklade länder och har cirka 30 medlemsländer. De publicerar
konjunkturrapporter, ekonomisk statistik och utredningar, men är även aktiv inom bl. a
förhandlingar om informationsutbyte med s.k. skatteparadis. BIS, Bank for international
settlements, baserat i Basel, Schweiz, är ett samarbetsorgan för centralbanker. Denna
organisation arbetar bl. a med gemensamma regler för bankers kapitaltäckning, även känt som
Basel II och Basel III.
1.8 Avkastningskurvan, korta och långa räntor
Som tidigare nämnts påverkas den korta räntan främst av Riksbankens beslut om reporäntan.
Räntan på längre löptider, däremot, påverkas bara i viss utsträckning av reporäntan. Andra
faktorer är väl så viktiga, inte minst marknadens bedömning av den framtida inflationen.
Inflation är dessutom ofta ett internationellt fenomen, så det föreligger tydliga samband
mellan de långa räntornas utveckling i olika länder. Om t ex. räntan på tyska statsobligationer
rör sig i en viss riktning är det normalt att även den långa räntan i Sverige rör sig åt samma
håll.
Räntestrukturen (från korta till långa räntor) för en viss låntagare, t ex. svenska staten, brukar
ofta sammanfattas i ett diagram kallat avkastningskurvan, med olika löptider på den
horisontella axeln och marknadsränta på den vertikala axeln. Avkastningskurvans utseende
varierar beroende på läget i ekonomin.
Vid t ex. lågkonjunktur är tillväxten låg eller till och med negativ och då brukar de korta
räntorna vara låga, eftersom centralbanken vill stimulera ekonomin och få till lite högre
inflation. Samtidigt kan de långa räntorna ligga relativt högt, eftersom marknaden ser framför
sig att ekonomin kommer att börja växa snabbare inom några år. Ett sådant läge hade vi senast
våren 2011.
På toppen av en högkonjunktur, däremot, kan inflationen vara på väg upp till för Riksbanken
besvärande nivåer. Då ligger normalt reporäntan högt, till och med högre än de långa
räntorna, eftersom Riksbanken vill dämpa ekonomin och inflationen. Senast detta hände i
Sverige var sommaren 2008, d.v.s. precis innan den akuta finanskrisen bröt ut.
11
2. Värdering av finansiella instrument
Ett av de viktigaste områdena inom finansiell ekonomi är hur man ska värdera olika
finansiella tillgångar. Vi är intresserade av att ta reda på vad man är villig att betala för ett
finansiellt instrument idag givet vilka (säkra eller osäkra) framtida kassaflöden, eller värden,
som instrumentet utlovar. Samma principer för att beräkna värdet idag tillämpas på alla typer
av finansiella instrument. I detta kapitel beskrivs hur värderingsmetodiken tillämpas på såväl
ränteinstrument som aktier. Men först några viktiga räntebegrepp.
2.1 Räntebegrepp
2.2 Enkel och effektiv ränta
Räntor uttrycks normalt som årsräntor, men det finns olika sätt att uttrycka en årlig ränta. I
dagens marknad betalar t ex. bolånekunder ofta en månadsränta på sina bolån. Då man betalar
räntan oftare än en gång per år, så blir det en skillnad mellan det vi kallar enkel årsränta och
effektiv årsränta. Ett exempel illustrerar skillnaden:
Exempel:
Kunden Janne har ett bolån med en räntesats på 3,8 %. Men han betalar räntan månadsvis. 3,8
% som står i lånehandlingen avser en s.k. enkel årsränta, vilket innebär att han betalar en
tolftedel av räntan varje månad. Hur hög är den effektiva årsräntan?
Svar: Effektiv årsränta tar hänsyn till ränta-på-ränta-effekten. Det förklaras av att i och med
att banken får in en tolftedel av 3,8 % redan den 31 januari så kan den låna ut det beloppet till
någon annan kund till 3,8 % enkel årsränta, och därmed får banken en ränta-på-ränta-effekt.
När vi räknar om från enkel till effektiv måste vi först räkna ut vad månadsräntan (även kallad
periodräntan) är i procent: 3,8 %/12 = 0,317 %. För att sedan få fram den effektiva årsräntan
tar vi 1 plus månadsräntan upphöjt till 12 och tar bort ettan, d.v.s. 1,00317 12 - 1 = 3,87 %
Vi kan även ställa oss frågan hur vi ska hantera läget, att vi får veta vad en kund har för
effektiv årsränta och hon undrar vilken enkel årsränta det motsvarar. Ja, då ska vi göra precis
tvärtom jämfört med ovanstående exempel. Vi testar det i nedanstående exempel:
Exempel:
Kunden Laila ha fått reda på att hennes SMS-lån har en effektiv årsränta på 23 %. Men
samtidigt betalar hon varje månad en viss ränta. Hon undrar hur hög den vanliga (d.v.s. enkla)
årsräntan är.
Svar: Den effektiva årsräntan är beräknad med månatlig ränta-på-ränta-effekt. För att ta sig
tillbaka från effektiv årsränta till månadsränta får vi då göra tvärtom jämfört med förra
exemplet: Vi tar ett plus den effektiva och tar tolfteroten ur det, minus ett för att få fram
månadsräntan, eller i siffror: 1,23(1/12) - 1 = 1,74%. Den enkla årsräntan blir då 12 * 1,74% =
20,88%
2.3 Nominell och real ränta
Nominell ränta avser hur mycket ränta vi tjänar i faktiska kronor och ören i förhållande till
insatt belopp. Real ränta, däremot, mäter hur mycket ränta vi tjänar när vi har justerat för
inflation, d.v.s. att den allmänna prisnivån på allt som vi köper har stigit. Det finns olika sätt
att beräkna den reala räntan enligt följande exempel:
12
Exempel: Nominell och real ränta
Nominell ränta 12%. Inflation 4%. Hur hög är realräntan?
Svar: Det finns en enkel metod och en lite mer komplicerad metod, och de mäter realräntan på
olika sätt.
Metod 1: Real ränta = nominell ränta - inflation = 12 - 4 = 8%
Metod 2: Real ränta = (1+ nominell ränta)/(1+inflation) - 1 = 1,12/1,04 - 1 = 7,7%
En skillnad i metoderna är att den enkla (Metod 1) mäter realränta i procent av penningvärdet
vid periodens början, medan den komplicerade (Metod 2) mäter realräntan i procent av
penningvärdet idag. Många föredrar det senare eftersom det ger en mer aktuell uppskattning
av hur mycket min reala förmögenhet ökat.
2.4 Nuvärde, slutvärde och annuiteter
Viktiga begrepp att känna till i värdering av finansiella instrument sammanfattas i följande
tabell:
Begrepp
Nuvärde
Framtida värde
Startvärde
Slutvärde
Innebörd
Värdet idag av ett framtida värde (kassaflöde)
Ett kassaflöde som betalas vid någon tidpunkt i framtiden
Belopp som investeras i ett finansiellt instrument idag
Ett förväntat framtida värde givet startvärdet
Det finns en koppling mellan de två begreppen nuvärde och startvärde, då de båda avser ett
belopp som betalas idag. Det finns vidare en koppling mellan begreppen framtida värde och
slutvärde, eftersom båda avser belopp som faller ut i en framtid. Frågan är då vad det är för
skillnad på nuvärde/framtida värde respektive startvärde/slutvärde. Svaret är att
nuvärde/framtida värde vet vi hur stort det framtida värdet är och vill ta reda på vad vi vill
betala idag, medan vid startvärde/slutvärde vet vi vilket belopp vi kan placera idag och vill
räkna ut hur stort framtida värde som krävs för att uppfylla vårt avkastningskrav.
Ett annat begrepp inom bank och finans är annuitet, och då kanske man först tänker på
annuitetslån, men annuitet kan även användas vid investeringar. Vi börjar med annuitetslånet.
Vad skiljer att vanligt lån från ett annuitetslån? För den kund som tar ett vanligt lån med
amortering, blir utgiften som störst i början av låneperioden, eftersom räntan beräknas på det
ursprungliga lånebeloppet. Men allt eftersom kunden amorterar på lånet så minskar
kvarvarande lånebelopp. Räntekostnaden blir därmed mindre och mindre under låneperioden
eftersom den beräknas på ett allt lägre belopp. I början av låneperioden har kunden alltså stora
utgifter på grund av stora räntebetalningar förutom amorteringen. I slutet av låneperioden är
amorteringen densamma, men räntebetalningen är liten. Till skillnad från ett vanligt lån så
jämnar ett annuitetslån ut kundens månadskostnad, så att den blir densamma för alla månader
under låneperioden. Totalsumman av ränta och amortering är alltså konstant. I början av
återbetalningstiden dominerar räntan, men i samma mån som räntedelen sedan minskar ökar
amorteringsdelen.
Annuitetsmetoden kan med fördel även användas för att utvärdera olika investeringsalternativ
med olika livslängd. När det gäller en investering så har man både kostnader och intäkter.
Kostnaderna kan t.ex. vara inköp av en maskin, amortering på lån eller nedskrivning av värdet
på grund av förslitning. Intäkterna kommer bl.a. från försäljningen av de varor maskinen
tillverkar. En investeringskalkyl enligt annuitetsmetoden går ut på att man fördelar en
13
investerings alla inbetalningar och utbetalningar i lika stora annuiteter över investeringens
livslängd. Det investeringsalternativ som har den högsta annuiteten, är den bästa investeringen
ekonomiskt sett, men alla investeringar med en positiv annuitet kan accepteras eftersom de
ger en vinst.
2.5 Diskonteringränta
Det som bestämmer förhållandet mellan ett framtida värde och nuvärdet kallas för
diskonteringsränta. Som synonymer förekommer även begreppen avkastningskrav eller
förväntad avkastning. För ett givet framtida värde antas vi kräva en ränta/avkastning som tar
hänsyn till hur lång tid det dröjer innan vi får kassaflödet samt hur säkert det är att kassaflödet
verkligen blir det vi förväntar oss. Operationen att beräkna ett nuvärde baserat på framtida
värden kallas för diskontering, och sker genom att vi dividerar det framtida värdet med en
faktor som består av1+ diskonteringsräntan justerat för hur lång tid vi måste vänta.
Exempel:
Förväntad framtida kassaflöde om ett år:
Diskonteringsränta (i årstakt):
Vad blir nuvärdet? Svar:
100 kr
4%
100/1,04 = 96,15 kr
Det vi har räknat ut här är att om vi placerar 96,15 kr idag och får 100 kr om ett år så har vi
haft en avkastning på exakt 4 procent. Som nämnts är tidpunkten för kassaflödet av stor
betydelse, eftersom vi uttrycker diskonteringsräntan som en avkastning per tidsenhet (normalt
per år).
Exempel:
Förväntat framtida kassaflöde om tre år:
Diskonteringsränta (i årstakt):
Vad blir nuvärdet? Svar:
100 kr
4%
100/1,043 = 88,90 kr
Not: 1,043 utläses som ett komma nollfyra upphöjt till 3 och det betyder 1,04*1,04*1,04
Finansiella instrument innehåller ofta utfästelser om flera framtida kassaflöden vid olika
tillfällen (t ex. kupongräntor på obligationer och utdelningar på aktier). Då måste vi göra en
beräkning för varje tidpunkt det faller ut en betalning. Om däremot två betalningar inträffar
samma dag (t ex. den sista kupongen och det nominella beloppet på en obligation) så kan de
adderas innan vi diskonterar.
En mycket viktig slutsats inom värdering av finansiella instrument är att diskonteringsräntan
och nuvärdet rör sig åt olika håll. Det förklaras enklast av att vi dividerar det framtida värdet
med 1 + diskonteringsräntan. Om diskonteringsräntan höjs, så faller nuvärdet, och tvärtom.
Det finns rikliga exempel där du har nytta av att känna till och förstå detta grundläggande
förhållande, när det gäller hur diskontering fungerar.
Exempel (jämför föregående exempel):
Förväntat framtida kassaflöde om tre år:
Diskonteringsränta (i årstakt):
Vad blir nuvärdet? Svar:
100 kr
3%
100/1,033 = 91,51
14
Med andra ord innebar en lägre diskonteringsränta (3% istället för 4%) att nuvärdet steg från
88,90 kr till 91,51 kr, vilket motsvarar cirka 3% och förklaras av att vi i det senaste exemplet
nöjde oss med en avkastning som var en procentenhet lägre i tre år.
Ett annat sätt att se på en placering är att givet ett visst startvärde, d.v.s. ett belopp som ska
placeras, och ett avkastningskrav så kan vi beräkna vilket slutvärde som skulle tillgodose vårt
avkastningskrav. I detta fall känner vi till beloppet idag (startvärdet), men är intresserade av
hur högt det framtida värdet måste vara, för att tillgodose vårt avkastningskrav. Då får vi
vända på steken och utgår från startvärdet och multiplicera upp med en räntefaktor som
brukar benämnas slutvärdefaktor.
Exempel:
Startvärde (belopp att placera idag):
Avkastningskrav (i årstakt):
Tidshorisont:
Slutvärde:
260 kr
5%
6 år
260 * 1,056 = 348,42
En relaterad frågeställning kan vara hur lång tid det tar att t ex. uppnå en fördubbling av ett
kapital givet en konstant årlig avkastning, d.v.s. hur många år måste man vänta innan man
uppnått en slutvärdefaktor på 2. Ett enkelt sätt att testa det är att räkna enligt föregående
exempel och testa olika antal år.
Exempel: Fördubbling av en placering
En placering väntas avkasta 7% årligen. Hur lång tid tar det för denna placering att fördubblas
i värde?
Svar: Testa dig fram på miniräknaren med t ex. 8 år: 1,078 = 1,72, höj till 10 år: 1,0710 = 1,97,
d.v.s. rätt svar är drygt 10 år. (1+ räntan, upphöjt i antal år ska bli två, eller nästan två)
2.6 Värdering av obligationer
Räntebärande instrument karaktäriseras av att de utlovar bestämda nominella (eller för vissa
instrument, reala) belopp i framtiden. Ränteinstrument med löptider upp till ett år brukar
kallas för penningmarknadsinstrument eller även diskonteringsinstrument.
Ränteinstrument med längre löptider än ett år kallas oftast för obligationer eller förlagslån.
Skillnaden mellan en obligation och ett förlagslån är att förlagslån är efterställda obligationer
om emittenten går i konkurs. De flesta obligationer och förlagslån har en årlig fastställd
räntebetalning som kallas kupong, som uttrycks som ett procenttal av nominellt belopp. Men
det förekommer även att instrumenten med lång löptid saknar separata räntebetalningar, och
då talar vi om s.k. nollkupongobligationer.
Ränteinstrument på den svenska marknaden handlas normalt genom att handlarna erbjuder
köp- och säljräntor för olika ränteinstrument. Dessa marknadsräntor motsvarar exakt den
diskonteringsränta som beskrivits i avsnitt 1.2 ovan. Det innebär att när man beräknar priset
på ett ränteinstrument så tar vi marknadsräntan och diskonterar obligationens kassaflöden.
Exempel:
Tvåårig obligation med nominellt belopp 100 kr, 3% kupongränta, marknadsränta 2%. Vad
blir priset?
Svar: Först måste vi beräkna kassaflödena: 3% av 100 kr i kupong om ett år och 3% kupong
och nominellt belopp 100 kr om två år, vilket ger: 3 kr om ett år och 103 kr om två år. Priset
15
räknas sedan ut enligt följande: Pris = 3/1,02 + 103/1,022 = 101,94 kr (kupongräntan
dividerad med 1 + marknadsräntan, upphöjt i antal år + kupongräntan och nominellt belopp
upphöjt i antal år)
En viktig effekt av hur diskontering fungerar är att löptiden till när vi får ett kassaflöde är av
stor betydelse. Ju längre löptid, desto större blir effekten av förändringar i
marknadsräntan. Ett enkelt exempel på det är följande: Om vi har två
nollkupongobligationer, Adam och Bertil, där Adam har en löptid på två år och Bertil har en
löptid på fem år. Båda handlas idag till marknadsräntan 2%. Vad händer med nuvärdet - priset
- på respektive obligation om marknadsräntan skulle stiga från 2 till 3%? För Adam måste vi
sänka priset med cirka 2%, eftersom vi kräver 1% högre avkastning per år i två år. För Bertil
måste vi sänka priset med cirka 5%, eftersom vi kräver 1% högre avkastning per år i fem år.
Hur mycket ett ränteinstruments pris förändras vid en förändring i marknadsräntan på en
procentenhet kallas för ränterisk.
Adam: 100/1,022= 96,12 kr Om räntan stiger till 3% 100/1,032 = 94,25kr (1,87/96,12 = ca 2%)
Bertil: 100/1,025= 90,57 kr Om räntan stiger till 3% 100/1,035 = 86,26kr (4,31/96,12 = ca 5%)
Därför är löptiden till när framtida kassaflöden infaller, mycket väsentlig för placeringar i
ränteinstrument. Det förklarar varför ett av de vanligaste nyckeltalen för ränteinstrument och
ränteportföljer och räntefonder är duration. Duration är ett mått på den vägda genomsnittliga
löptiden, på alla framtida kassaflöden (kuponger och nominella belopp) för ett
ränteinstrument eller en portfölj av räntepapper. Vägningen sker genom att man beräknar
nuvärdet av alla kassaflödena och därmed hur stor andel varje kassaflödes nuvärde utgör av
totalen. Det ger en indikativ uppfattning om hur stor förändringen i nuvärdet blir vid en
förändring i marknadsräntan med en procentenhet. Sättet att beräkna duration (att väga med
respektive kassaflödes andel av det totala värdet) innebär även att om man jämför två
obligationer med samma löptid, så gäller att ju högre kupongränta, desto kortare duration
och desto lägre ränterisk. Det beror på att utbetalningen av högre kuponger, väger tyngre
som andel av en obligations totala värde.
Man brukar säga att om man behåller en obligation tills den förfaller, så vet man vilken
avkastning man får. Det gäller för nollkupongobligationer, men inte för vanliga obligationer
som har kupongutbetalningar. I värderingen av en obligation utgår man ifrån att man kan
återinvestera de framtida kupongutbetalningarna till den nu rådande räntan, men den framtida
räntan vet vi inget om. Återinvesteringsrisk kallas risken att framtida kassaflöden från en
obligation måste återinvesteras till lägre räntor än den obligationen erbjuder idag.
Ytterligare en faktor att ta hänsyn till vid placeringar i räntebärande instrument är risken att en
emittent inte kan fullgöra sina utlovade kassaflöden, vilket kallas för kreditrisk. Den
etablerade metoden för att avgöra ett ränteinstruments kreditrisk är kreditbetyg. Sett till den
internationella räntemarknaden finns det tre dominerande företag som sätter kreditbetyg på
alla sorters ränteinstrument: Standard & Poors, Moody's och Fitch. Alla tre tillämpar likartade
skalor som har högsta betyg AAA (alt. Aaa), följt av AA, A, BBB, BB, B, CCC, CC och C,
därefter antas emittenten gå i konkurs (ibland kallat betyg D för eng. default). Det går en
viktig skiljelinje mellan betygen BBB och BB i och med att allting från BBB och bättre
benämns investment grade och allting från BB och neråt benämns speculative grade.
Investment grade kan på svenska kallas för kreditvärdiga obligationer, medan speculative
grade ofta kallas junk bonds eller på svenska skräpobligationer.
16
Generellt gäller att marknadsräntorna är högre ju lägre kreditbetyget är för en emittent.
Dessutom gäller att en viss emittents obligationer har högre kreditbetyg än samma emittents
förlagslån, vilket innebär att de senare har högre marknadsränta. Den höga marknadsräntan på
speculative grade jämfört med statsobligationer kan från ett värderingsperspektiv ses som en
kombination av två faktorer, dels en viss risk för konkurs, dels ett högt avkastningskrav från
placerarna.
Typiska låntagare inom respektive kreditbetyg sammanfattas i tabellen nedan.
Tabell: Typiska låntagare i olika kreditbetygsnivåer
Kreditbetyg
AAA
AA
A
BBB
BB
B
CCC
Exempel på låntagare
Stabila stater (Norge, Sverige, Finland, Tyskland m fl.)
Bästa bankerna (Nordea, Handelsbanken)
Banker med lite sämre kreditvärdighet, stabila andra företag
Företag med lite sämre finansiell ställning
Företag med ganska väsentligt sämre ställning
Ughh!
Ukraina
Sedan finanskrisen bröt ut för några år sedan har det blivit alltmer populärt att placera i
företagsobligationer. De nya fonder som dykt upp kan heta olika saker, men det viktigaste att
känna till när det gäller företagsobligationsfonder är i vilken utsträckning de placerar i
investment grade eller speculative grade. De fonder som kallar sig för high yield brukar
investera i speculative grade och har därmed väsentligt högre kreditrisk och högre
samvariation med aktiemarknaden.
2.7 Värdering av aktier
Aktier skiljer sig på många punkter från obligationer. Några viktiga skillnader sammanfattas i
nedanstående tabell.
Tabell: Skillnad mellan aktier och obligationer
Faktor
Placeringshorisont
Framtida kassaflöden
Diskonteringsränta
Obligationer
Normalt fastställd
Normalt fastställda
Den marknaden handlar på
Aktier
Normalt inte fastställd
Ej fastställda (utdelningar)
Ej fastställt
Med andra ord så är egentligen ingenting fastställt när det gäller aktier, jämfört med att för
obligationer så är för det mesta allting fastställt. Det är med andra ord inte så konstigt att
värderingen av aktier på marknaden, är så avsevärt mer osäker än för obligationer. Det finns
dock sätt att hantera de olika osäkerhetsmomenten med aktier. När det gäller den ej fastställda
placeringshorisonten, kan vi konstatera att kassaflöden som faller ut långt in i framtiden, inte
har särskilt stort nuvärde idag, vilket innebär att fokus när det gäller aktievärdering ligger på
bolagets utveckling under de närmaste 10-15 eller säg 20 åren. Beträffande bolagens vinster
och utdelningar får man lägga ned ett arbete med att göra så bra prognoser som möjligt, vilket
en hel sektor inom finansbranschen har som huvuduppgift. När det gäller diskonteringsränta/
avkastningskrav finns det sannolikt en relativt stor samsyn på marknaden vid givna tillfällen
om vad som är ett rimligt avkastningskrav.
17
Den traditionellt dominerande modellen att värdera aktier överensstämmer helt med
angreppssättet i avsnitten 2.5 och 2.6 ovan. Skillnaden är att kassaflödena här, är de ej i
förväg kända utdelningarna samt att placerare själva måste bestämma avkastningskrav
(diskonteringsränta). Modellen kallas på engelska för Dividend Discount Model. På svenska
kallas den diskonteringsmodellen även om den ordagrant översatt skulle heta
utdelningsdiskonterings-modellen. För att illustrera att den fungerar precis som motsvarande
prisberäkning för obligationer redovisas nedanstående exempel:
Exempel:
Ett bolag väntas ge en utdelning nästa år på 10 kr, om två år 11 kr och om tre år 11,50 kr.
Bolagets aktiekurs efter utdelningen om tre år väntas uppgå till 190 kr. Vad blir motiverad
kurs om avkastningskravet sätts till 8 %?
Svar: Pris = 10/1,08 + 11/1,082 + (11,50+190)/1,083 = 178,65
Det kanske inte alltid är så lätt att ha en uppfattning om vad bolaget ska vara värt efter
utdelningen om tre år. För att hantera detta problem är det vanligt att man gör ett antagande
som förenklar beräkningen, nämligen att man - i brist på annan unik information - antar att
bolaget efter år tre ska fortsätta växa i en jämn takt, ofta satt till samma takt som hela
marknaden, s.k. konstant tillväxt under överskådlig framtid (kallas även för Gordonmodellen). I det läget kan man tillämpa en matematisk metod som förenklar beräkningen av
vad bolaget borde vara värt om tre år och sätter in detta värde istället för prognosen 190 kr.
Vid aktievärdering är det annars vanligt att man studerar olika nyckeltal. Här kommenteras de
tre vanligaste som båda förekommer i dagstidningarnas börstabeller.
P/E-tal är en kvot mellan aktiekursen (P) och vinsten per aktie (E för eng. earnings per share).
Det vanligaste sättet att uttrycka P/E-tal är att ta dagens aktiekurs dividerat med prognosen för
det kommande årets vinst per aktie, ofta uttryckt som genomsnittet av analytikers prognoser.
Det är även möjligt att använda detta nyckeltal för att värdera aktier (d.v.s. beräkna en
motiverad kurs). Aktieanalytiker har ofta en uppfattning om t ex vad som är ett rimligt P/E-tal
för en viss bransch, typ banker eller verkstadsbolag. Givet att de då gör en egen prognos på
bolagets vinst nästa år kan motiverad kurs beräknas genom att multiplicera med rimligt PEtal, se exempel nedan:
Exempel:
En analytiker har räknat ut att ett bolag i verkstadsindustrin kommer att ha en nettovinst efter
skatt nästa år på 12 kr per aktie. Samtidigt anser hon att ett rimligt PE-tal för bolaget ifråga är
14. Samtidigt står aktien i 125 kr. Är detta ett köp, behåll eller sälj läge?
Svar: Motiverad kurs kan beräknas som vinst per aktie gånger rimligt PE-tal, d.v.s. 12*14 =
168 kr. Det är med andra ord ett starkt köpläge.
PE-talet för hela Stockholmsbörsen har de senaste åren legat på cirka 12-13, vilket är en
relativt låg nivå jämfört med de senaste decennierna. Detta kan tolkas antingen som att
placerarna har en negativ prognos för framtida vinster eller att de har blivit mindre
riskbenägna (eller en kombination av båda dessa faktorer).
Ett annat vanligt nyckeltal är direktavkastning. Det beräknas vanligen genom att ta
prognosen på nästa års utdelning dividerat med dagens aktiekurs. Det är med andra ord ett
mått i procent, som kan jämföras med t ex. marknadsräntan på obligationer. En intressant
iakttagelse i detta sammanhang är att direktavkastningen på Stockholmsbörsen under senare
tid legat kring 3,5% jämfört med en marknadsränta på statens långa obligationer på cirka
18
1,5%. Under hela perioden sedan andra världskriget, har räntan på statens obligationer
överstigit direktavkastningen på aktier. Men sedan en tid tillbaka är den alltså inte ens hälften
så hög. Det ger en indikation på att antingen är statens obligationer övervärderade eller så är
svenska aktier undervärderade (eller både och).
Substansvärdet används ofta vid en värdering av investmentbolag som t.ex. Investor och
Industrivärden. Substansvärdet definieras som marknadsvärdet för bolagets aktieportfölj
minskad med dess lånade kapital (nettoskuld). Substansvärdet per aktie i ett bolag betraktas
av många investerare som ett mycket viktigt nyckeltal inför ett köp- eller säljbeslut. På börsen
är de flesta investmentbolag värderade med en substansrabatt, dvs. bolagets börsvärde
understiger dess substansvärde.
2.8 Värdering av optioner
Optioner är avtal om köp eller försäljning av ett underliggande instrument, vid en framtida
tidpunkt, till ett förutbestämt pris. Till skillnad från en termin har innehavaren av en option
ingen skyldighet att köpa (eller sälja) vid den framtida tidpunkten. Optionsinnehavaren har
däremot rättigheten att göra det om det är fördelaktigt, men utnyttjar inte optionen om det är
ofördelaktigt.
Den som innehar rätten att köpa äger en köpoption och den som har rätten att sälja äger en
säljoption. Innehavaren av en köpoption har således rätten (men inte skyldigheten) att köpa
det underliggande instrumentet till det förutbestämda priset, som i detta sammanhang kallas
lösenpris. På motsvarande sätt har innehavaren av en säljoption rätten (men inte
skyldigheten) att sälja det underliggande instrumentet till lösenpriset.
För att innehavaren av en köp- eller säljoption, ska ha någon reell möjlighet att utnyttja sin
rätt att köpa respektive sälja det underliggande instrumentet, måste det finnas någon som
tillhandahåller det motsatta affärsintresset (kom ihåg, derivat är nollsummespel). Vad är det
motsatta intresset i förhållande till en köpoption, dvs. rätten att köpa det underliggande
instrumentet till lösenkursen? Jo, det är skyldigheten att sälja om innehavaren av köpoptionen
väljer att utnyttja sin rätt, dvs. begära lösen. Rätten att köpa saknar innehåll om det inte
någonstans finns en skyldighet att sälja det som innehavaren av köpoptionen har rätten att
köpa. På motsvarande sätt måste det för varje säljoption finnas en motsvarande skyldighet att
köpa det som innehavaren av säljoptionen har rätten att sälja. Att tillhandahålla det motsatta
intresset till rätten att köpa eller sälja det underliggande instrumentet till lösenkursen, faller
naturligt nog, på de aktörer som utfärdar köp- och säljoptioner. Notera den viktiga skillnaden
mellan att sälja en option som man redan äger (köp- eller säljoption) och att utfärda en
option, dvs. medverka i tillskapandet av en option som inte fanns tidigare.
Att utfärda en köpoption är alltså att acceptera skyldigheten att sälja om innehavaren av
köpoptionen vill utnyttja sin rätt. Att utfärda en säljoption innebär på motsvarande sätt en
skyldighet att köpa. I utbyte får de aktörer som utfärdar optioner en ersättning i form av en
premie. Premien är priset för rätten att köpa eller sälja det underliggande instrumentet till
lösenkursen. Denna premie betalas av optionens innehavare till utfärdaren. Eftersom derivat
är ett nollsummespel motsvaras alla vinster av lika stora förluster. Om optionen inte utnyttjas
får utfärdaren behålla hela premien, vilket i så fall blir en förlust för innehavaren. Om
optionen utnyttjas och ger upphov till en vinst för innehavaren, då är det utfärdaren som gör
den motsvarande förlusten.
19
Innehavare
Utfärdare
KÖP
Rättighet att köpa
Betalar premie
Skyldighet att sälja
Erhåller premie
SÄLJ
Rättighet att sälja
Betalar premie
Skyldighet att köpa
Erhåller premie
Den ekonomiska innebörden illustreras bäst av ett resultatdiagram. I figuren nedan
åskådliggörs vad värdet av en köpoption med lösenpriset 150 kr skulle bli, för olika kurser på
slutdagen. Om priset på det underliggande instrumentet är lägre än150 kr på slutdagen
förfaller optionen värdelös, dvs. optionens värde skulle bli noll. Det är i så fall billigare att
köpa aktien i marknaden, än det är att utnyttja optionen och köpa den till lösenpriset 150 kr.
Om marknadspriset är högre än 150 kr blir det förmånligt för innehavaren av optionen att
utnyttja sin rätt att köpa aktien till 150 kr.
25,0
20,0
Figur 1Värdet av en köpoption med
lösenpriset 150 kr på slutdagen
15,0
Realvärde
10,0
5,0
0,0
-5,0
-10,0
En options värde på slutdagen kallas för
Realvärde, dvs. det värde som optionen har
-25,0
om man antar att den underliggande varan,
120
130
140
150
160
170
180
t.ex. aktien inte kommer att röra sig mer innan
Pris underliggande
optionen går till lösen. Köpoptionen sägs
därför ha ett positivt realvärde, om priset på det
underliggande instrumentet, är högre än lösenkursen. Realvärdet är skillnaden mellan kursen
på aktien och lösenkursen på optionen, under förutsättning att aktiekursen är högre än
lösenpriset. Om priset på aktien stiger till 160 kr blir realvärdet 10 kr. Om priset på aktien
stiger ytterligare till 170 kr fördubblas realvärdet till 20 kr. Realvärdet på en option är
antingen positivt eller noll, dvs. aldrig negativt.
-15,0
-20,0
Det är viktigt att påpeka att den som köper en option (köp- eller säljoption) aldrig riskerar att
förlora mer än premien. Optioner liknar därför försäkringar. Man betalar en premie och får
ersättning i form av ett positivt resultat, under förutsättning att en viss händelse inträffar, dvs.
under förutsättning att optionens realvärde blir positivt. Den maximala vinsten för utfärdaren,
som tillhandahållit försäkringen och därför bär risken, är premien som får behållas ograverad
om händelsen inte inträffar. Om den maximala förlusten för den som köper en option är
begränsad till premien, så kan förlusten för den som utfärdar en option bli mycket stor.
Nettoresultatet för båda parter (men med omvänt tecken för utfärdaren) är skillnaden mellan
optionens värde och premien. Om optionen är värd mindre än premien, har innehavaren
fortfarande gjort en nettoförlust och utfärdaren därför en nettovinst. Detta illustreras i
figurerna nedan. Figur 2 Innehavaren av köpoptionen förlorar hela premien, som i detta fall
antagits vara 7,50 kr per aktie, om aktiekursen är lägre än lösenpriset på slutdagen. Om
aktiekursen är högre än 150 kr minskar förlusten och om värdet på optionen överstiger 7,50 kr
blir nettoresultatet för innehavaren positivt. Detta inträffar när priset på det underliggande
instrumentet överstiger 157,50 kr (lösenpris + premie). Det exakt motsatta resultatet uppstår
för utfärdaren av optionen (figur 3).
20
Figur 2 Resultat på slutdagen av innehavd köpoption
med lösenpriset 150 kr om premien är 7,50 kr
25,0
20,0
15,0
Resultat
10,0
5,0
0,0
-5,0
-10,0
-15,0
-20,0
-25,0
120
130
140
150
160
170
180
Pris underliggande
25,0
Figur 3 Resultat på slutdagen av utfärdad köpoption
med lösenpriset 150 kr om premien är 7,50 kr
20,0
15,0
Resultat
10,0
5,0
0,0
-5,0
-10,0
-15,0
-20,0
-25,0
120
130
140
150
160
170
180
Pris underliggande
Innehavaren av en säljoption har köpt en försäkring mot att den underliggande aktien ska
falla. En nettoförlust som motsvarar premien blir resultatet för innehavaren om aktien inte
faller. I figurerna nedan har premien på säljoptionen antagits vara 6 kr. Det betyder att
innehavaren av säljoptionen förlorar maximalt 6 kr per aktie. Om den underliggande aktien
faller under lösenpriset 150 kr minskar förlusten. Om aktien faller under 144 kr
(lösenpris - premie) gör innehavaren en vinst, och utfärdaren en lika stor förlust.
Figur 4 Resultat på slutdagen av innehavd säljoption
med lösenpriset 150 kr om premien är 6 kr
25,0
20,0
15,0
Resultat
10,0
5,0
0,0
-5,0
-10,0
-15,0
-20,0
-25,0
120
130
140
150
160
170
180
Pris underliggande
21
Figur 5 Resultat på slutdagen av utfärdad säljoption
med lösenpriset 150 kr om premien är 6 kr per aktie
25,0
20,0
15,0
Resultat
10,0
5,0
0,0
-5,0
-10,0
-15,0
-20,0
-25,0
120
130
140
150
160
170
180
Pris underliggande
Marknadspriset på en option, dvs. premien, har två beståndsdelar – dels ett realvärde som vi
har visat ovan, dels ett tidsvärde. Tendensen för tidsvärdet är att det faller successivt under
optionens löptid allt eftersom dagarna går, och slutar på noll på slutdagen. Detta är emellertid
en grov förenkling eftersom tidsvärdet inte bara beror på den återstående löptiden eller räntan
utan också på den underliggande aktiens volatilitet (dvs. standardavvikelse), som kan variera
betydligt över tiden. Man kan säga att tidsvärdet avspeglar osäkerheten i vilken kurs som den
underliggande aktien har på lösendagen. Om det är lång tid kvar till lösendagen, samtidigt
som volatiliteten är hög (svängningarna är stora) i marknaden, är tidsvärdet högt eftersom det
är svårt att säga på vilken nivå kursen slutar. Men om det är kort tid kvar till lösendagen och
volatiliteten samtidigt är liten, är osäkerheten kring slutkursen säkrare och tidsvärdet därmed
mindre.
Värdet av en option beror alltså på flera faktorer:
 priset på den underliggande aktien
 optionens lösenpris
 optionens löptid
 aktiens volatilitet
 den riskfria räntan
Av dessa faktorer är aktiens volatilitet (svängningar i kurs) det svåraste att observera, men det
är volatiliteten som i de flesta lägen påverkar optionens värde allra mest. En stigande
volatilitet ger i normalfallet stigande premier. Handel med optioner förutsätter därför att man
har ett dubbelt grepp om det underliggande instrumentet, inte bara kursutveckling utan också
volatilitet. Medan aktier och räntebärande instrument kan köpas och behållas mer eller mindre
långsiktigt kräver derivat fortlöpande uppföljning.
Bilden nedan illustrerar förenklat vilken optionsposition man ska ha utifrån sin marknadstro.
22
3. Risk och avkastning
Ett väsentligt område inom finansiell ekonomi handlar om att kunna beräkna avkastning och
risk. I detta avsnitt presenteras viktiga samband och beräkningsmetoder i form av enkla
räkneexempel i syfte att underlätta förståelse.
3.1 Lägesmått - Aritmetiskt och geometriskt medelvärde
När man ska bedöma en fonds värdeutveckling över flera perioder, t ex fem år, finns det olika
sätt att beräkna den totala och den genomsnittliga avkastningen. De kallas för aritmetisk
respektive geometrisk kalkyl och illustreras enklast med ett exempel.
Exempel:
En fond har haft en avkastning under de senaste fem åren på: +12,-14,+28,-10,+3.
Vad blev den totala respektive genomsnittliga avkastningen per år?
Svar: Det finns som sagt två metoder:
1. Aritmetisk metod: +12-14+28-10+3 = 19 %, medelvärde 19/5 = 3,8%
2. Geometrisk metod: 1,12*0,86*1,28*0,9*1,03-1 = 14,3%, medelvärde 1,1431/5 = 2,71%
Skillnaden mellan aritmetisk och geometrisk kalkyl är att den geometriska på ett korrekt sätt
tar hänsyn till att fondvärdet förändras mellan åren, d.v.s. den tar med en ränta-på-räntaeffekt. Därför är det den metoden som på ett korrekt sätt beskriver hur fonden i verkligheten
har utvecklats. Det innebär att man beräknar som om man hade haft en placering med
konstant 2,71 % ränta per år med ränta-på-ränta-effekt.
Varför håller man då överhuvudtaget på med den andra metoden, aritmetiskt medelvärde? Jo,
den kan vara intressant om man från ett historiskt perspektiv vill undersöka hur ett typiskt år
på aktiemarknaden kan förväntas bli. Då är det inte frågan om någon ränta-på-ränta-effekt,
utan vad tror vi om aktiemarknaden på ett års sikt, och då är det snarast aritmetiskt genomsnitt
som är mer intressant. Denna beräkning är ett vanligt medelvärde dvs. man summerar värdet
av antalet observationer och dividerar med antalet.
3.2 Direktavkastning och värdeförändring
I tidigare avsnitt definierades direktavkastning som förväntad aktieutdelning i procent av
aktuell aktiekurs. När vi ska mäta upp den totala avkastningen på en placering så består den
av summan av direktavkastning och värdeförändring. Det kan illustreras i följande exempel:
Exempel:
Kunden Karin köpte en aktie för 83 kr. Knappt ett år senare fick hon en utdelning på 3 kr.
Strax därefter sålde hon aktien för 92 kr. Vilken blev hennes totala avkastning på denna
placering?
Svar: Total avkastning = (3+92)/83 - 1 = 14,5%
3.3 Faktisk och förväntad avkastning och risk
Inom finansiell ekonomi är det viktigt att hålla isär begreppen förväntad avkastning och
faktisk (realiserad) avkastning. I och med att olika finansiella instrument har olika grader av
risk (spridning i avkastning) kommer de faktiska avkastningarna sällan att överensstämma
med vad som utgjort förväntad avkastning. Det senare begreppet är likafullt mycket viktigt i
och med att det utgör grunden för hur finansiella instrument värderas idag.
23
3.4 Riskfri ränta och riskpremie
Ett av de svåraste problemen inom finansiell ekonomi, är att fastställa rimliga avkastningskrav
(diskonteringsräntor), för olika typer av finansiella instrument. Ett vanligt sätt är att utgå från
en riskfri placering (riskfri ränta), som beroende på placeringshorisont kan utgöras av korta
eller långa statspapper, utgivna av en stat med god kreditvärdighet (t ex svenska staten). Det
vi därutöver kräver i form av högre avkastningskrav för att vi tar risker brukar kallas för
riskpremie. Generellt gäller att ju högre risk en placering har, desto högre riskpremie kan vi
förvänta oss att kunderna kräver.
3.5 Risktyper
Risk innebär osäkerhet om framtida utfall. Inom finansiell ekonomi avser det utfall på olika
placeringar. Det finns ett antal olika typer av risk, som i olika grad kan påverka utfallet av
finansiella placeringar enligt följande tabell:
Tabell: Olika typer av risk
Risktyp
Marknadsrisk
Beskrivning
Volatilitet (d.v.s. svängningar) i marknadsnoterade tillgångar, t ex.
aktiekurser, index, ränterisk på obligationer, valutarisk i utländska
tillgångar
Risken att en emittent av räntepapper ställer in betalningarna. Gäller även
Kreditrisk
s.k. motpartsrisk vid handel med OTC-derivat, t ex valutaterminer
Likviditetsrisk Risken att en placerare inte kan sälja ett innehav utan att påverka
marknadspriset, t ex stora svenska småbolagsfonder
Operativ risk Risken för mänskliga faktorn eller datasystem, kriser (t ex. en orkan i
New York - börsen stänger i två dagar)
En filosofisk kommentar till denna indelning är att såväl kreditrisker som likviditetsrisker i
normalfallet har effekt på det vanligaste måttet på marknadsrisk (spridning i avkastning som
presenteras i nästa avsnitt). Operativa risker däremot brukar förvaltare/fondbolag få stå för.
3.6 Spridningsmått: varians och standardavvikelse
Särskilt aktier och aktiemarknaden generellt brukar variera mycket i värde. Svängningar i
värde brukar vi ofta kalla för volatilitet. Frågan är hur man kan mäta volatiliteten. Det
vanligaste måttet på spridning kallas för standardavvikelse. Det måttet utgör kvadratroten ur
det egentliga spridningsmåttet som kallas för varians. Vi återkommer närmare till hur man
kan tolka måttet standardavvikelse i konkreta situationer. Men för att förstå var det kommer
ifrån redovisas nedan ett exempel på hur man först beräknar varians för att sedan kunna
beräkna standardavvikelsen.
Exempel:
En fond har haft följande avkastning i procent de senaste fem åren: -5,+10,+15,+3,-8.
Vad har denna fond haft för spridning mätt som varians och standardavvikelse?
Svar: Först måste vi beräkna det aritmetiska medelvärdet (jfr avsnitt 3.1 ovan): (-5+10+15+38)/5 = 3%
24
Sedan beräknar vi varje års avvikelse från detta medelvärde enligt följande:
– 5-3
= -8
+10-3
= +7
+15-3
= +12
+3-3
=0
– 8-3
= -11
Sedan tar vi dessa avvikelser i kvadrat (så att även negativa avvikelser bidrar till vårt mått på
volatiliteten). Summa kvadrater av avvikelser: (-8)2+72+122+02+(-112) = 378, dividera med 5:
378/5 = 75,6. D.v.s. variansen är den genomsnittliga kvadraten på avvikelserna från
medelvärdet. Standardavvikelen är kvadratroten av variansen: roten ur 75,6 = 8,7 %
Sambandet mellan standardavvikelse och varians ska du kunna. Testa på miniräknaren! 8,7
upphöjt i 2 (x2) blir 75,6 precis som roten ur (√) 75,6 blir 8,7. Vad betyder då en
standardavvikelse på 8,7%? Jo att avkastningen utifrån medelvärdet på 3%, har varierat med
en standardavvikelse +8,7% uppåt från medelvärdet dvs. (3+8,7=) +11,7% och neråt från
medelvärdet (3+ -8,7%=) dvs. -5,7%, under perioden. Standardavvikelsen bygger på den s.k.
normalfördelningen, som är en statistisk modell, vilket vi återkommer till alldeles strax.
Vad är då en normal standardavvikelse för olika placeringar? Generellt kan vi konstatera att
volatiliteten på aktiemarknaden sedan millennieskiftet har präglats av tre olika och väldigt
distinkta perioder.
Den första sträckte sig från millennieskiftet fram till botten på aktiemarkaden kring årsskiftet
2002/2003. Därefter följde en stabilt stigande marknad ända fram till sommaren 2007 som
dessutom präglades av mycket låg volatilitet. Sedan inleddes finanskrisen, som medförde förutom en kraftig nedgång i aktiemarknaderna - en dramatiskt ökad volatilitet.
Diagram: Rullande 24 månaders standardavvikelse på Stockholmsbörsen
35%
30%
25%
20%
15%
10%
5%
0%
dec-11
dec-10
dec-09
dec-08
dec-07
dec-06
dec-05
dec-04
dec-03
dec-02
dec-01
dec-00
dec-99
dec-98
dec-97
dec-96
dec-95
dec-94
Källa: Ecowin, Nasdaq OMX
För att ge en uppfattning om olika placeringars volatilitet under senare år presenteras
standardavvikelse för ett antal svenska stora bolag i följande tabeller.
25
Tabell: Standardavvikelse i årstakt för svenska aktier (60 månader från nov.2007 t o m okt
2012)
Bolag eller index
OMXSPI (börsen)
AstraZeneca
Swedish Match
TeliaSonera
Hennes & Mauritz
SCA B
Handelsbanken A
SKF B
Atlas Copco B
Skanska B
Ericsson B
Nordea
Volvo B
Standardavvikelse i årstakt (%)
21,1
18,8
19,7
20,6
20,9
28,3
29,2
30,2
31,0
31,1
31,7
36,1
43,2
Källa: Nasdaq OMX
En intressant första iakttagelse är att de första fyra aktierna, som kan kallas för stabila, ickecykliska bolag, till och med har lägre volatilitet än hela börsen, vilket inte är vad vi förväntar
oss om man jämför en enskild aktie med hela marknaden (som är en någorlunda
väldiversifierad portfölj, se vidare kapitel 4 nedan). Vidare bör man inse att tabellen ovan
omfattar en speciell tidsperiod som innehåller den värsta finansiella krisen på sju decennier,
så man kanske inte kan förvänta sig att detta upprepas framöver. I övrigt är det typiskt
cykliska verkstadsbolag (SKF, Atlas och Volvo), bygg (Skanska) och banker (Handelsbanken
och Nordea) som stått för hög standardavvikelse. Att bankerna legat så högt under denna
period har även det att göra med finanskrisen i och med att den började i bankerna för att
sedan sprida sig till industrin.
Svenska fonder redovisar årlig standardavvikelse som en del av rekommenderade nyckeltal.
Den beräkningen baseras på 24 månaders avvikelser från medelvärdet, men räknas om till
årstakt. Ju högre standardavvikelse, desto större svängningar har fonden haft (och normalt
sett, kan förväntas ha i framtiden). Dock är måttet standardavvikelse svårt att relatera till det
som kunder upplever som verklig risk, vilket är risken att förlora pengar. Det finns emellertid
ett sätt att utnyttja nyckeltalet standardavvikelse för att beskriva för kunder hur stor risken för
att förlora pengar är.
Ett vanligt antagande är att avkastningen på aktiemarknaden följer den s.k.
normalfördelningen. Det är en sannolikhetsfördelning som är väldigt vanlig i naturen och i
verkligheten i övrigt. Den användes som bas för det gamla betygssystemet med betygen 1-5.
Det var flest 3:or, lite färre (och lika många) 2:or och 4:or, samt ganska få (och lika många)
1:or och 5:or. Egenskaperna är således att utfallen tenderar ofta att ligga nära medelvärdet, ju
större avvikelser från medelvärdet desto sällsyntare. Normalfördelningen beskrivs ofta i form
av ett diagram som beskriver hur ofta saker inträffar inom olika intervall, i vårt fall avkastning
på aktiemarknaden. I nedanstående diagram har detta testats för Affärsvärldens Generalindex
från 1950 till 2008 månadsvis. Vad detta diagram visar är att aktiemarknaden i Sverige är
någorlunda följsam med vad som antas enligt den statistiska fördelningen normalfördelning.
Innebörden av det är mycket viktig eftersom det betyder att det enda spridningsmått som
behövs för att analysera risken i olika portföljer är varians/standardavvikelse.
26
Dessutom kan man ha nytta av måttet standardavvikelse på ett mer handfast sätt i en
kunddiskussion enligt följande. Om vi kan fastställa någon sorts förväntad avkastning på en
fond, säg en Sverigefond, och har en uppfattning om fondens standardavvikelse, så kan man
göra följande uttalanden om fondens förväntade spridning (risk).
Exempel: Förväntad avkastning, standardavvikelse och normalfördelning
Givet att vi antar att aktiemarknadens avkastning är normalfördelad, så är det möjligt att
beskriva förväntad framtida spridning, baserat på endast förväntad avkastning och
standardavvikelse:
En fond har en förväntad långsiktig genomsnittlig avkastning på 8%. Samtidigt är den
förväntade framtida standardavvikelsen 18%. Vad kan man säga om den förväntade framtida
spridningen i denna fonds resultat?
Svar: Enligt normalfördelningen så kommer cirka 2 av 3(66,7%) utfall att ligga inom ett
intervall som sätts av medelvärdet +/- en standardavvikelse, d.v.s. i det här fallet mellan 8-18
= -10 % och 8+18 = +26%. Eftersom kunden inte är så bekymrad om fonden går upp mer än
+26%, så kan vi fokusera på nersidan. Hur ofta går den här fonden sämre än -10 %? Jo,
hälften vart tredje år, d.v.s. vart sjätte år.
27
4. Avkastning och risk i portfölj
Det som kallas för modern portföljteori utvecklades från början i USA av en ekonom vid
namn Harry Markowitz (som delade Riksbankens pris till Alfred Nobels minne år 1990).
Portföljteorin bygger på vissa statistiska metoder samt antaganden om hur placerare beter sig.
Ett viktigt antagande är att placerare endast baserar sina placeringsbeslut på förväntad
avkastning och risk (mätt som varians/standardavvikelse). I detta och senare kapitel beskrivs
Markowitz modeller för hur man ska välja portföljer. Detta kapitel handlar om hur man mäter
avkastning och risk i en portfölj med flera tillgångar.
4.1 Avkastning i portfölj
Att mäta avkastningen i en portfölj med flera tillgångar är ett exempel på aritmetiskt
medelvärde (eller på svenska: genomsnitt). Dock måste vi ta hänsyn till hur stor andel varje
tillgång har i portföljen, därför kan det kallas för vägt aritmetiskt medelvärde. Ett exempel
illustrerar detta:
Exempel:
En portfölj består av följande aktier med olika stor andel av portföljen. Swedish Match: andel
0,4, förväntad avkastning 10%, Alfa Laval: andel 0,3, förväntad avkastning 9%, SCA andel
0,3, förväntad avkastning 8%. Vad blir den förväntade avkastningen i portföljen?
Svar: Ta andelen av portföljen gånger det vägda aritmetiska medelvärdet enligt följande:
Förväntad avkastning portfölj: (0,4*10) + (0,3*9) + (0,3*8) = 9,1%
Testa på miniräknaren. Fundera också alltid över om resultatet verkar rimligt. Hela portföljen
är 1,0 dvs. 100%.
4.2 Samvariation (korrelation)
När man sätter ihop portföljer med olika tillgångar, så kommer portföljens risk att bero på, i
vilken utsträckning de olika tillgångarna rör sig (utvecklas) tillsammans eller i olika riktning.
Om vi har en portfölj med två tillgångar som alltid rör sig i olika riktning så skulle det till om
med vara möjligt att åstadkomma en helt riskfri portfölj, eftersom uppgångar i den ena
tillgången helt skulle motsvaras av nedgångar i den andra. Sådana par av tillgångar är dock
inte så vanliga i praktiken (snarast obefintliga).
Samvariation mäts liksom spridning med två olika mått. Det vanligaste och mest begripliga
kallas för korrelationskoefficient (eller kort: korrelation)1. Det trevliga med det måttet är att
det finns gränser för vilka värden det kan anta. Det kan aldrig vara lägre än -1 och det kan
aldrig vara högre än +1. Dessutom anger dessa båda extremvärden speciella beteenden hos
olika par av tillgångar.
Om korrelationen är -1 så har vi ett par av tillgångar som alltid rör sig i olika riktning, vilket
som sagt är väldigt ovanligt i praktiken. Dock förekommer det fonder som via derivat
positionerar sig så att de systematiskt rör sig i motsatt riktning mot aktiemarknaden, t ex Xact
Bear, som har en korrelation mot marknaden på -1.
Vid en korrelation på +1 så har vi två tillgångar som alltid samtidigt rör sig åt samma håll.
Även detta är ovanligt, men kanske t ex. Ericsson B och Ericsson A borde röra sig någorlunda
åt samma håll för det mesta. Sedan finns det olika grader mellan -1 och +1. De flesta aktierna
1
Ett annat mått på samvariation heter kovarians
28
på en börs tenderar att ha positiv korrelation. Korrelationen tenderar att vara lägre om vi
jämför bolag i olika branscher. Normala korrelationer mellan olika aktier tenderar att ligga
mellan säg 0,0 och 0,8.
Tabell: Exempel på korrelation mellan aktier i samma bransch
(60 månader från nov.2007 t o m okt 2012)
Kombination
Atlas Copco B - SKF B
Atlas Copco B - Volvo B
SKF B - Volvo B
SHB A - Nordea
Korrelation
0,90
0,80
0,75
0,80
Tabell: Exempel på korrelation mellan aktier i olika branscher
(60 månader från nov.2007 t o m okt 2012)
Kombination
AstraZeneca - HM
AstraZeneca - SCA
Ericsson B - Skanska B
Ericsson B - SHB A
Korrelation
0,12
-0,09
0,00
0,07
Källa: Nasdaq OMX
4.3 Risk i portfölj
Varför är då korrelation intressant från vårt perspektiv? Jo för att det är en väldigt avgörande
faktor för att bestämma risken i en portfölj med flera tillgångar. Ju lägre korrelation mellan
tillgångarna i en portfölj, desto oftare rör de sig i olika riktningar. Därmed blir risken i
portföljen desto lägre.
Vid beräkningen av risken i en portfölj med flera tillgångar beror risken dels på spridningen
(variansen/standardavvikelsen) i respektive tillgång, dels på den parvisa korrelationen mellan
alla tillgångar.
För att illustrera betydelsen av korrelation kan vi studera nedanstående exempel. Den visar
exempel på portföljer med två olika aktier med olika förväntad avkastning (10 resp. 12 %)
och olika standardavvikelse (15 resp. 16 %). Graferna beskriver vilken risk och förväntad
avkastning en portfölj med dessa två aktier skulle ha, givet olika antaganden om korrelationen
mellan de två aktierna
29
Förväntad Diagram: Portfölj med två aktier, olika korrelation
avkastning
12.5
12.0
11.5
korr = 0
11.0
korr = 0,5
korr = 1
10.5
10.0
9.5
10
11
12
14
13
Risk (standardavvikelse)
15
16
17
Det enklaste alternativet att analysera detta exempel är att studera portföljer med lika vikt i
båda aktierna dvs. 50% i vardera, vilket innebär läget vid 11 % avkastning. Om korrelationen
är lika med +1 så följer vi den räta linjen och hamnar på en risk på 15,5%, vilket är lika med
den genomsnittliga standardavvikelsen på de båda aktierna. Om korrelationen däremot vore
0,5 (vilket innebär att de båda aktierna ganska ofta rör sig åt olika håll) så blir risken i den
likavägda portföljen cirka 13,5%, d.v.s. klart lägre än risken i var och en av aktierna. Om den
ena tillgången vore en hedgefond som lever upp till sin utfästelse att ha ingen korrelation med
aktiemarknaden så skulle man kunna uppnå den låga risken med korrelation noll, vilket ger en
standardavvikelse på cirka 11 %.
4.4 Diversifiering
Hur en portfölj beter sig med hänsyn till samvariationen mellan olika tillgångar, ger även en
konkret ledtråd till vad man bör eftersträva i sammansättningen av en portfölj: låg korrelation.
Det är bakgrunden till att många kapitalägare och -förvaltare aktivt söker efter
placeringstillgångar som har en låg korrelation med det som brukar utgöra den största delen
av risken i portföljen, nämligen aktieplaceringar. Det är motivet för det som ibland kallas
Alternativa Investeringsstrategier (AIS). Nackdelen med många sådana (t ex
råvaror/metaller, fastigheter och hedgefonder) är att de ofta har sämre likviditet och därmed
inte prissätts lika ofta som marknadsnoterade tillgångar, vilket kan ge en förskönad bild av
lägre volatilitet och korrelation med aktiemarknaden.
30
5. Marknadsmodellen, systematisk och specifik risk
I Markowitz ursprungliga portföljvalsmodell (som beskrivs närmare i följande kapitel)
behövde man beräkna korrelationen mellan varje par av aktier, vilket innebar väldigt många
beräkningar. Därför försökte man i slutet av 1950-talet att förenkla beräkningen av risk i en
portfölj. Det blev det som kallades marknadsmodellen som presenteras i detta avsnitt. Denna
utveckling ledde till att analysen av aktier och portföljer utvecklades i termer av olika
riskkällor såsom systematisk och specifik risk. Detta kapitel beskriver marknadsmodellen och
de intressanta slutsatser vi kan dra avseende aktier och portföljer från de olika nyckeltal som
kommer fram i marknadsmodellen.
5.1 Marknadsmodellen
Marknadsmodellen var från början ett sätt att förenkla beräkningen av risken i en portfölj.
Den baseras på att alla aktier istället för att parvis jämföras med varandra bara jämförs med
marknaden (ett brett marknadsindex). Det innebär väsentligt färre mätningar per aktie och
minskar dramatiskt behovet av beräkningar.
För att åstadkomma detta tillämpades en statistisk metod som kallas regression. Den innebär
att man studerar samtidiga observationer av en akties och marknadens avkastning, och
undersöker det systematiska sambandet mellan aktien och marknaden, eller uttryckt på ett
annat sätt: i vilken utsträckning marknadens avkastning förklarar aktiens avkastning.
Sambandet mellan en aktie och marknaden kan lättast studeras genom att konstruera ett
diagram som visar dels marknadens avkastning på x-axeln (den horisontella), dels aktiens
avkastning på y-axeln (den lodräta). Ett exempel på detta visas nedan:
Diagram: Skanska B jämfört med OMXSPI
40%
30%
Skanska B
20%
10%
0%
-20%
-10%
0%
10%
20%
30%
-10%
-20%
OMXSPI
Not: OMXSPI är ett index över samtliga aktier på Stockholmsbörsen (s.k. prisindex). Källa Nasdaq OMX.
Varje punkt i diagrammet representerar två månadsobservationer, en för Skanska som läses av
på y-axeln och en för börsen som läses av på x-axeln. Hur punkterna fördelar sig i
31
diagrammet ger en översiktlig bild över i vilken utsträckning Skanska följer (alternativt inte
följer) börsen upp och ned. Det vi kan observera är bland annat att de flesta punkterna ligger
uppe till höger eller nere till vänster, vilket ger en tydlig bild av en positiv korrelation.
Fler exempel på denna typ av diagram presenteras nedan, då kompletterade med resultatet av
den statistiska metoden regression, som utgör ett sätt att i siffror (och diagram) sammanfatta
det systematiska sambandet mellan aktien och börsen.
5.2 Beta m fl. regressionsresultat
Det systematiska sambandet mellan en aktie och marknaden beskrivs av i vilken utsträckning
aktien rör sig vid en given rörelse i marknaden. I diagrammet nedan beskrivs det av lutningen
på den inplacerade trendlinjen och denna lutning kallas för beta. Beta är ett mått på aktiens
känslighet för rörelser i marknaden, och kallas därför ofta för marknadsrisk (vilket är lite
olyckligt eftersom begreppet marknadsrisk även betecknar en tillgångs totala risk). Det
genomsnittliga beta-värdet för hela marknaden är definitionsmässigt 1, vilket i ett diagram
som beskriver en akties avkastning i förhållande till marknadens avkastning motsvarar en
vinkel på 45 grader. Aktier med högre beta har en större benägenhet att röra sig när
marknaden rör sig jämfört med aktier med lägre beta.
Alfa är var trendlinjen skär y-axeln och utgör ett mått på i vilken utsträckning aktien gått bra
(positivt alfa) eller dåligt (negativt alfa) i förhållande till marknaden.
Epsilon är feltermerna, d.v.s. hur mycket observationerna avviker från trendlinjen i vertikal
riktning. Den genomsnittliga feltermen är noll (det är så alfa är konstruerat), men spridningen
i feltermer har sin betydelse, vilket vi återkommer till nedan.
I de tre följande diagrammen återges exempel på tre aktiers rörelser i förhållande till
marknaden med resultatet av regressionen inritat i form av en rät linje (trendlinje) som utgör
en sammanfattning av det systematiska sambandet. Trendlinjens läge och lutning bestäms av
resultaten för beta (linjens lutning) och alfa (var trendlinjen skär y-axeln).
Diagram: Skanska jämfört med OMXSPI med trendlinje
40%
y = 1,0045x + 0,0015
R2 = 0,4631
30%
Skanska B
20%
10%
0%
-20%
-10%
0%
10%
-10%
-20%
-30%
OMXSPI
32
20%
30%
Diagram: Volvo jämfört med OMXSPI med trendlinje
40%
y = 1,7757x + 0,004
R2 = 0,7499
30%
20%
Volvo B
10%
0%
-20%
-10%
0%
10%
20%
30%
-10%
-20%
-30%
-40%
OMXSPI
Diagram: Swedish Match vs OMXPI med trendlinje
20%
y = 0,2835x + 0,0096
R2 = 0,0923
Swedish Match
10%
0%
-20%
-10%
0%
10%
20%
30%
-10%
-20%
OMXSPI
För att underlätta en jämförelse mellan de tre ovanstående diagrammen är skalorna satta till
samma nivå. Om vi börjar med beta-värdet beskrivs det av lutningen. Då kan vi konstatera att
Skanskas trendlinje har en lutning som motsvarar 45 grader, d.v.s. mitt emellan noll och 90
grader. Det innebär att Skanska hade ett beta-värde på 1 under perioden. Sett till Volvo kan vi
konstatera att lutningen på trendlinjen är väsentligt större, och det kan uttryckas i termer av
beta-värdet, som uppgår till hela 1,78. Tolkningen av det är, att när marknaden rörde sig en
procent, så reagerade Volvo med hela 1,78 %. Ett motsatt exempel är det tredje diagrammet
som beskriver sambandet mellan Swedish Match och börsen. Dess trendlinje är väsentligt
flackare än både Volvos och Skanskas, och det kan vi uttrycka med beta-värdet som endast
uppgår till 0,28. Det innebär att för varje procent förändring på börsen så följde Match bara
med till 0,28 %.
Beträffande alfa-värdena kan de läsas av där respektive trendlinje skär y-axeln. Såväl Volvo
som Skanska hade alfa-värden nära noll, medan Match, vilket är tydligt i diagrammet, hade ett
positivt alfa-värde, som uppgick till 0,96 %, d.v.s. detta var en mycket bra period för Swedish
33
Match. Nivån +0,96% låter inte så imponerande, men då bör man tänka på att detta avser per
månad, så i årstakt överträffade Match index - rensat för följsamheten med marknaden - med
närmare 12%.
Det tredje nyckeltalet från regressionen är som nämnts epsilon, vilket kallas fel term och som
mätt som medelvärde är noll. För en enskild månad, däremot brukar det vara antingen positivt
eller negativt och kan i diagrammet läsas ut som det vertikala avståndet mellan en punkt och
trendlinjen.
Av dessa tre resultat (beta, alfa och epsilon) är det framför allt beta-värdet som har intresse.
Det mäter som nämnts en akties (eller portföljs) benägenhet att följa med i marknadens
rörelser upp eller ned. Därför brukar den kallas marknadsrisk (inte att sammanblanda med
total volatilitet som mäts med standardavvikelse). Den kallas även systematisk risk, eftersom
den mäter det systematiska sambandet mellan börsen och aktien.
Tabell: Exempel på betavärden
Bolag eller index
OMXSPI (börsen)
AstraZeneca
Swedish Match
TeliaSonera
Hennes & Mauritz
SCA B
Handelsbanken A
SKF B
Atlas Copco B
Skanska B
Ericsson B
Nordea
Volvo B
Standardavvikelse i årstakt (%)
21,1
18,8
19,7
20,6
20,9
28,3
29,2
30,2
31,0
31,1
31,7
36,1
43,2
Beta-värde
1,00
0,09
0,28
0,51
0,51
0,82
1,01
1,12
1,22
1,00
0,69
1,40
1,78
Månadsvis november 2007 - oktober 2012. Källa: Nasdaq OMX, egna beräkningar
För att underlätta en jämförelse upprepas siffrorna för standardavvikelse för respektive aktie
från tabellen ovan. Det framgår klart att de stabila aktierna med låg standardavvikelse har
väldigt låga beta-värden, inom 0,09-0,51. Ett beta-värde på t ex 0,5 är vad man skulle förvänta
sig av en blandfond med hälften aktier och hälften räntor. Samtidigt har de volatila cykliska
aktierna höga beta-värden. En udda fågel i denna jämförelse är Ericsson som trots hög
standardavvikelse har ett lågt betavärde på 0,69.
5.3 Systematisk och specifik risk
Med hjälp av marknadsmodellen kan man dela upp risken i en aktie eller portfölj i två typer
av risk: systematisk risk (även kallad marknadsrisk) och specifik risk (även kallad
företagsspecifik, unik och diversifierbar risk). Sett från figuren ovan kan den specifika risken
förklaras av hur stor spridningen i feltermerna (epsilon) är. När man beräknar den specifika
risken tar man helt enkelt feltermerna (avvikelserna från trendlinjen) i kvadrat och beräknar
medelvärdet av detta. Ju större spridning på feltermer, desto större specifik risk.
Sambandet är Total risk = systematisk risk + företagsspecifik risk.
34
5.4 Diversifiering sett från marknadsmodellen
Utifrån analysen av de två risktyperna i marknadsmodellen - systematisk och specifik - kan
man illustrera effekten av diversifiering (riskspridning) med följande diagram som beskriver
vad som händer i en portfölj när man ökar antalet aktier
Diagram: Antal aktier och risk i en portfölj
4,5
4
Total risk
3,5
3
Specifik
risk
Risk
2,5
2
1,5
Systematisk risk
1
0,5
0
1
3
5
7
9
11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
Antal aktier
Diagrammet visar vad som händer i en portfölj när man ökar antalet aktier. Den systematiska
risken, som vi inte kan diversifiera bort, bibehålls ungefär konstant (förutsatt att det
genomsnittliga beta-värdet hålls konstant, sannolikt nära ett). Den risk typ som diversifieras är
den specifika, ofta kallad företagsspecifika risken. När portföljen diversifierats så mycket att
all specifik risk har eliminerats, har vi skapat en indexportfölj som bara har systematisk risk.
6. Portföljvalsteori
Den s.k. moderna portföljteorin lanserade i början av 1950-talet av en amerikansk ekonom
vid namn Harry Markowitz. Hans portföljteori byggde vidare på hur man beräknar
avkastning och risk i portföljer som redovisades i kapitel 4. Vi skulle enligt Markowitz
beräkna förväntad avkastning, risk och samvariation för alla aktier och sedan testa alla
möjliga portföljer man skulle kunna sätta ihop för att få tag på de bästa möjliga portföljerna.
Senare lade man till möjligheten att investera i en riskfri tillgång, vilket ändrade
förutsättningarna och valmöjligheterna. Vidare utvecklades i början av 1960-talet den s.k.
Capital Asset Pricing Model (förkortat CAPM), som även den resulterade i ett pris från
Riksbanken 1990 till William Sharpe. Den utgör utöver dess starka rekommendation om hur
placerare bör bete sig, även en värderingsmodell som ger ett konkret förslag till vilken
diskonteringsränta man bör tillämpa för olika riskfyllda tillgångar.
35
6.1 Effektiva portföljer
När väl Markowitz hade etablerat metoden för att beräkna risken i olika portföljer var hans
nästa steg att testa alla möjliga olika portföljer med avseende på förväntat avkastning och risk.
Uppgiften var att hitta de bästa möjliga portföljerna av alla möjliga portföljer. De portföljer
som Markowitz definierade som s.k. effektiva portföljer kan beskrivas på två olika sätt:
1. För en given risknivå, hitta den portfölj som har högst förväntad avkastning
2. För ett givet avkastningskrav, hitta den portfölj som har lägst förväntad risk
Det intressanta med dessa två beskrivningar är att de leder fram till samma portföljer, vilket
beror på hur olika portföljers avkastning och risk tenderar att formera sig, vilket beskrivs i
nästa avsnitt.
6.2 Effektiv front, utan och med riskfri tillgång
För att illustrera möjliga portföljer och effektiva portföljer konstruerades ett diagram som
beskrev risk på x-axeln och förväntad avkastning på y-axeln. Från "molnet" av ett oändligt
antal möjliga portföljer kunde man från detta diagram identifiera vilka portföljer som var
överlägsna alla andra alternativa portföljer - den effektiva fronten.
Diagram: Exempel effektiva fronten
9
Förväntad avkastning
8
7
6
5
4
3
2
1
0
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18
Standardavvikelse
Så småningom kom man på att det även finns en riskfri tillgång att placera i, t ex korta
statspapper. Dessa kan rent teoretisk antas ha en standardavvikelse på noll, och dessutom vet
vi vad den är vid varje tillfälle. Detta ledde till att Markowitz effektiva front för
aktieportföljer kompletterades med denna riskfria tillgång. Effekten av detta var dramatisk,
eftersom det gav möjligheter att konstruera portföljer som var bättre än Markowitz effektiva
portföljer av riskfyllda tillgångar. Den räta linjen i diagrammet nedan representerar olika
blandningar av riskfri tillgång och den aktieportfölj som precis snuddar Markowitz effektiva
front, vilket brukar kallas för tangentportföljen. Denna uppfinning var grunden för den s.k.
separationsteorin, som innebär att en placerare alltid ska hålla samma portfölj av riskfyllda
tillgångar och reglera risknivån i sin totala portfölj med inslaget av riskfri placering längs den
36
räta linjen. Jämfört med Markowitz effektiva front behöver man alltså inte byta aktieportfölj
om man ska ändra risken i sin portfölj - det gör man med andelen riskfri tillgång.
Diagram: Effektiva fronten med riskfri tillgång
9
Förväntad avkastning
8
7
6
5
4
3
2
1
0
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18
Standardavvikelse
Separationsteorin visade att blandportföljer som innehöll olika andelar riskfri tillgång och
tangentportföljen var överlägsna andra effektiva riskfyllda portföljer. En annan fördel med
dessa portföljer är att det är väsentligt enklare att beräkna risken i en blandportfölj än i en
portfölj med olika riskfyllda tillgångar (förutsatt att vi vet förväntad avkastning och risk i
tangentportföljen).
Exempel: Förväntad avkastning och risk i en blandportfölj
I diagrammet ovan är den riskfria räntan 3,5%. Tangentportföljens standardavvikelse är 10%
och dess förväntade avkastning 6%. Hur hög blir den förväntade avkastningen och risken i en
portfölj som till 75 % består av tangentportföljen och 25 % riskfri tillgång?
Svar:
Portföljens förväntade avkastning: (0,75*6) + (0,25*3,5) = 5,375 %
Portföljens risk: (0,75*10) + (0,25*0) = 7,5 %
Testa med miniräknaren! Förväntad avkastning: Andelen av portföljen gånger portföljens
avkastning + andelen riskfri tillgång gånger avkastningen på den riskfria tillgången. Risken:
Andelen av portföljen gånger portföljens risk + andelen riskfri tillgång gånger risken på den
riskfria tillgången
6.3 Effekt av belåning
Sett till diagrammet ovan så ligger den räta linjen högre än den effektiva fronten även till
höger om tangentportföljen. I detta fall representerar den räta linjen att man investerar i
tangentportföljen med belåning, vilket förutsätter att vi kan låna till riskfri ränta. Även i denna
del av diagrammet ligger den räta linjen högre än den effektiva fronten för riskfyllda
tillgångar. Av det kan vi dra slutsatsen att portföljteorin rekommenderar att det är bättre att
37
endast äga den väldiversifierade tangentportföljen och belåna den, snarare än att byta till en
mer riskfylld aktieportfölj utan belåning.
Vad blir då effekten av att belåna en investering i tangentportföljen med avseende på
förväntad avkastning och risk? Här kan vi faktiskt tillämpa precis samma metod som i
exemplet ovan.
Exempel: Förväntad avkastning och risk i en belånad portfölj
Riskfri ränta (=lika med låneränta) 3,5 %, förväntad avkastning tangentportfölj 6%, förväntad
risk tangentportfölj 10%. Vad blir förväntad avkastning och risk i en tangentportfölj som är
belånad med 50% (d.v.s. vi har köpt tangentportföljen för 150 % av vår förmögenhet och
lånat 50% av vår förmögenhet till riskfri ränta)?
Svar:
Portföljens förväntade avkastning: (1,5*6) – (0,5*3,5) = 7,25 %
Portföljens risk: (1,5*10) = 15 %
I verkligheten är det inte så många placerare som tillämpar dessa principer (även om belåning
förekommer bland riskvilliga privatpersoner). Men det finns ett exempel som har en stor
kundkrets i Sverige, nämligen förvaltaren av icke-väljarnas premiepension, Sjunde APfonden. Deras aktiefond består av en global aktieindexportfölj som kan belånas upp till 1,5
gånger fondförmögenheten.
Att belåna en riskfylld portfölj innebär att risken för nettoförmögenheten ökar proportionellt
mot belåningen, i exemplen ovan från 10% till 15% standard avvikelse. Att ytterligare ta
hänsyn till vid belåning är vad som kan inträffa om aktiemarknaden plötsligt skulle rasa, vad
har det för effekt på den återstående nettoförmögenheten? I Sjunde AP-fondens fall bevakas
graden av belåning ständigt, men samma kanske inte gäller mindre placerare med belånade
aktieportföljer. Följande exempel illustrerar detta.
Exempel: Effekt av en marknadsnedgång på risken i en belånad portfölj
Ursprunglig belånad portfölj som i ovanstående exempel. Aktieportföljen faller med 25% i
samband med en kraftig börsnedgång. Hur stor är risken i den kvarvarande portföljen om
ingen åtgärd vidtas?
Svar: Om vi antar att nettoförmögenheten var 100 kr och den belånade aktieportföljen var 150
kr innebär en nedgång med 25% att aktieportföljen faller till 150*(1-0,25) = 112,5 eller med
37,5 kr. Då har nettoförmögenheten fallit från 100 kr till 62,5 kr. Aktieportföljens storlek i
förhållande till nettoförmögenheten blir 112,5/62,5 = 1,8. Risken blir 1,8*10 = 18%
Exemplet visar att risken i placerarens nettoförmögenhet ökar om värdet på aktieportföljen
faller. Det bör hanteras (inte minst eftersom banken kräver det) genom att risken reduceras i
form av att sälja aktier. En följdfråga är om det är lämpligt att sälja aktier när börsen har fallit
med 25%, men det är vad som kan bli nödvändigt för en placerare med en högt belånad
aktieportfölj.
6.4 Capital Asset Pricing Model (CAPM)
I början av 1960-talet växte en modell fram kallad Capital Asset Pricing Model (CAPM).
Den byggde på separationsteoremet och en rad av antaganden om placerares beteenden. Det
viktigaste antagandet var dock att i CAPM antog man att alla placerare hade samma
förväntningar vad avser förväntad framtida avkastning, risk och samvariation. Innebörden av
detta antagande var att samtliga placerare på marknaden har samma effektiva front för
38
riskfyllda tillgångar. Dessutom har ju alla placerare samma riskfria ränta. Det ledde fram till
slutsatsen att alla placerare ska ha samma portfölj av riskfyllda tillgångar. Hur är det enda
sättet som man kan åstadkomma detta? Jo genom att alla placerare ska äga en portfölj som
innehåller alla världens riskfyllda tillgångar vägda med marknadsvärde (d.v.s. en global
indexportfölj) och reglera risken genom att variera andelen riskfri tillgång. Det illustreras i
följande diagram som kallas Capital Market Line och förkortas CML.
Diagram: Capital Market Line, CML, effektiv front enligt CAPM
9
Marknadens
förväntade
avkastning
Förväntad avkastning
8
Tangentportfölj=
global marknadsportfölj
7
6
5
4
3
2
Marknadens
standardavvikelse
1
0
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16 17 18
Standardavvikelse
6.5 CAPM som värderingsmodell: bara systematisk risk förtjänar en riskpremie
Förutom att CAPM utgör en portföljvalsmodell som rekommenderar att vi alla ska placera i
en global portfölj av riskfyllda tillgångar, så är det även en värderingsmodell. Om man följer
CAPMs rekommendation att bara lägga alla sina riskfyllda placeringar i ett globalt index,
innebär det i termer av risktyperna i marknadsmodellen i föregående kapitel, att man helt kan
undvika specifik risk. CAPM anger då att det inte vore rimligt att förvänta sig en riskpremie
för en risk typ - specifik risk - som man lätt kan undvika genom att placera i ett globalt
marknadsindex med riskfyllda tillgångar.
Istället är det endast den systematiska (ej diversifierbara) risken som bör förtjäna en
riskpremie. Den systematiska risken mäter vi ju från marknadsmodellen med beta-värdet för
olika riskfyllda tillgångar (aktier, fonder m m). Enligt CAPM ska riskpremien på en riskfylld
tillgång vara proportionell mot tillgångens beta-värde i förhållande till riskpremien på
marknaden.
Exempel: Avkastningskrav enligt CAPM
Marknadens förväntade avkastning 6%, riskfri ränta 3,5%, aktiens beta-värde 1,2. Vad blir
förväntad avkastning (=avkastningskrav eller diskonteringsränta) för aktien enligt CAPM?
Svar: Marknadens förväntade riskpremie: 6-3,5 = 2,5 %. Förväntad riskpremie på aktien:
1,2*2,5 = 3 %, förväntad avkastning på aktien: 3+3,5 = 6,5 %
39
Detta samband mellan beta-värdet och förväntad avkastning beskrivs ofta i form av
nedanstående diagram, som beskriver hur hög förväntad avkastning ska vara enligt CAPM,
givet en tillgångs beta-värde. Den utgår från riskfri avkastning, d.v.s. med en tillgång som har
ett beta-värde på noll avkastningskravet vara lika med riskfri ränta. Med ett beta-värde över
noll så stiger riskpremien i takt med beta-värdet. Det brukar kallas för Security Market Line
och förkortas SML. På svenska kallas det ofta värderingslinjen för värdepapper.
Diagram: Security Market Line (SML)
8%
Förväntad avkastning
7%
6%
5%
4%
3%
2%
1%
0%
0
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
1
1,1 1,2 1,3 1,4
Beta-värde
7. Utvärdering av portföljer och fonder
En mycket angelägen uppgift inom finansiell ekonomi och av stort intresse för kunden, är att
utvärdera kapitalförvaltares resultat, för att välja förvaltare som kan förväntas ha en god
framtida utveckling. Det kan ske på många olika sätt. Utvärderingar av kapitalförvaltare kan
dels ske genom att analysera portföljers historiska avkastning, dels genom s.k. kvalitativ
utvärdering av förvaltaren och förvaltningsorganisationen. Detta kapitel beskriver de
vanligaste kvantitativa metoderna, hur kvalitativ utvärdering kan ske, vanliga jämförelseindex
samt fondbetyg.
7.1 Riskjusterad avkastning
Om portföljteorin stämmer så bör portföljer med högre risk ha högre avkastning. Det är
bakgrunden till att man vid utvärdering av portföljavkastning önskar att rensa bort effekten av
skillnader i portföljers risk och beräkna det vi kallar riskjusterad avkastning. Det finns ett
antal väletablerade mått på riskjusterad avkastning, som kommer att beskrivas och
exemplifieras nedan. De riskjusterar med olika riskmått och beräknas på olika sätt. Vilket
mått som ska användas beror på placerarens situation och intresse, d.v.s. det finns inte ett enda
"rätt" mått på riskjusterad avkastning. Generellt för dessa mått på riskjusterad avkastning
gäller att de ska vara så höga som möjligt (placerarna vill ha så hög avkastning som möjligt
även efter riskjustering).
40
Två problem kvarstår även efter man har tagit hänsyn till risken vid utvärdering. Det ena är att
bra historisk riskjusterad avkastning, sällan innebär lika god framtida riskjusterad avkastning.
Det kan uttryckas som att avkastning sällan är stabil över tiden samt att god historisk
avkastning ofta följs av medelmåttig avkastning i framtiden. Ett annat problem vid tolkningen
av god historisk avkastning är att det inte är så lätt att, bland de portföljer som har haft god
riskjusterad avkastning, urskilja dem som haft det på grund av skicklighet, från dem som helt
enkelt har haft tur. Det är motivet till att de flesta som arbetar med portföljutvärdering
(konsulter, förvaltare av fondandelsfonder m fl.) även nyttjar sig av och komplettera med
kvalitativ analys i syfte att skilja ut de skickliga från de ”turliga”.
7.2 Sharpe-kvoten
Samma William Sharpe som var ledande i utvecklingen av CAPM har gett namn åt det kanske
vanligaste måttet på riskjusterad avkastning, nämligen Sharpe-kvot. Som vi konstaterat i
tidigare kapitel bör placerare kräva högre avkastning för att ta högre risk. Det Sharpe-kvoten
frågar sig är hur hög ersättning har jag fått per enhet risk, eller annorlunda uttryckt, hur stor
blev den realiserade riskpremien per enhet risk (mätt som standardavvikelse). Enheten i denna
kvot är just en kvot, vi dividerar riskpremie i procent med standardavvikelse i procent, så
kvoten mäter förhållandet mellan riskpremien och standardavvikelsen.
Sharpe-kvoten kan i många fall vara svårtolkat eller till och med ganska oanvändbar. För t ex
aktiefonder bestäms den realiserade riskpremien till största delen av hur marknaden har
utvecklats, och om den har fallit så har de allra flesta aktiefonder negativ Sharpe-kvot. Det är
ett läge som snarast liknar situationen för P/E-tal för aktier: är den negativ så är den mindre
intressant och beräknas ofta inte. Vid positiv marknadsutveckling kan den däremot ge en god
bild av huruvida förvaltarna av aktiefonder har fått betalt för eventuella högre risker jämfört
med index. Emellertid är Sharpe-kvot inte så vanlig för att utvärdera bl. a aktiefonder
eftersom deras avkastning till så stor del avgörs av marknadens utveckling.
För en annan fondkategori - hedgefonder - är däremot Sharpe-kvoten det allra viktigaste
måttet på riskjusterad avkastning. Eftersom Sharpe-kvoten mäter riskpremien, d.v.s.
meravkastningen i förhållande till riskfri ränta, så överensstämmer det exakt med
avkastningsmålet för de allra flesta hedgefonder. Positiv Sharpe-kvot för en hedgefond
innebär uppnådd ambition (samt att man kan ta ut resultatbaserat arvode).
Exempel: Tre hedgefonders avkastning och risk 60 månader t o m oktober 2012
Fond
Brummer Multistrategy
Brummer Nektar
Excalibur
Årlig avkastning
5,9
12,2
7,5
Risk (standardavvikelse)
3,9
7,7
4,4
Källa: Moneymate
Hur hög blev respektive fonds Sharpe-kvot och påverkade det rangordningen (riskfri ränta var
1,7 %)?
Svar:
Brummer Multistrategy: (5,9 - 1,7)/3,9 = 1,08 (tredje bäst)
Brummer Nektar: (12,2 - 1,7)/7,7 = 1,36 (bäst)
Excalibur: (7,5 - 1,7)/4,4 = 1,32 (näst bäst)
Ja, ordningen förändrades efter att riskjusteringen har gjorts.
Årlig avkastning minus riskfri ränta dividerat med standardavvikelsen.
41
Alla tre fonderna har uppnått strålande resultat för riskjusterad avkastning mätt med Sharpekvot. En Sharpe-kvot överstigande 1 utgör en exceptionellt god avkastning för en hedgefond.
Multistrategy är en fond som består av Brummers olika fonder, och den uppnår mycket god
diversifiering genom att de ingående fonderna (bl. a Nektar) har mycket låg samvariation.
Både Nektar och Excalibur arbetar mer med räntemarknader än de flesta hedgefonder (som i
Sverige ofta håller på med aktier, s.k. long-short equity). De har relativt olika risknivå, så när
man beräknar Sharpe-kvoten för dessa två visar det sig att de har praktiskt taget samma
riskjusterade avkastning, där dock Excalibur kör med en mindre riskfylld strategi.
7.3 Jensens alfa
Enligt CAPM ovan så bör man inte förvänta sig någon riskpremie för att ta specifik risk. Det
Jensens alfa frågar sig: blev det så i verkligheten avseende en historisk period? D.v.s. har en
portfölj lyckats uppnå en positiv riskpremie för att ta specifik risk, vilket även kan kallas alfa.
Jensens alfa är inte helt identiskt med det alfa som uppträder i marknadsmodellen eftersom
den baseras på CAPM, som även tar hänsyn till riskfri ränta. Emellertid är beta-värdet
detsamma i marknadsmodellen, CAPM och för Jensens alfa.
Enligt CAPM utgör den förväntade riskpremien endast beta-värdet gånger marknadens
riskpremie. Det Jensens alfa beräknar är om det historiskt har förekommit någon skillnad
jämfört med CAPM givet en portföljs betavärde under samma period. Om en portfölj har
utvecklats bättre än vad den borde enligt CAPM, så kan det tolkas som att förvaltaren har
varit skicklig (eller haft tur) när det gäller aktieurval ("stock picking"), d.v.s. att tjäna på att ta
specifik risk.
Exempel: Jensens alfa
En aktiefond hade under en period en genomsnittlig årlig avkastning på 14%. Samtidigt gick
börsen (inkl. utdelningar) 13% årligen. Riskfri ränta uppgick till 4% per år. Fondens
betavärde uppgick till 1,2. Hur hög blev fondens Jensen-alfa?
Svar: Förväntad avkastning enligt CAPM 4+1,2*(13-4)= 14,8% men fonden avkastade endast
14%. Jensen-alfa = 14-14,8= -0,8 Fonden borde tack vare sin höga marknadsrisk (beta-värde
1,2) ha gått hela 1,8 procentenheter bättre än index (14,8-13) enligt CAPM. Men den slog
bara index med en procentenhet (14-13=1). Det innebär att fondens aktieurval ("stock
picking") bidrog negativt med 0,8 procentenheter.
7.4 Treynorkvot
Treynorkvoten liknar Sharpekvoten, men istället för att relatera meravkastningen över den
riskfria räntan mot portföljens standardavvikelse (total risk), så relaterar man den mot
portföljens beta (marknadsrisk).
7.5 Tracking Error och informationskvot
Ett vanligt nyckeltal för portföljer är Tracking Error eller aktiv risk. Det mäter i vilken
utsträckning en portföljs avkastning avviker från sitt jämförelseindex. Det beräknas vanligen
genom att månatliga skillnader mellan portföljen och index beräknas, och för dessa avvikelser
beräknas en varians och standardavvikelse. Det normala sättet att redovisa dessa är omräknat i
årstakt, precis som standardavvikelsen i en portföljs totala svängningar. Skillnaderna mellan
en portföljs avkastning och index är normalt väsentligt mindre än portföljens totala
42
svängningar, vilket innebär att Tracking Error normalt är väsentligt mindre än den totala
risken i portföljen.
Tracking Error visar hur stora avvikelser portföljens sammansättning har jämfört med
indexportföljens. Ju större avvikelser i portföljinnehav, desto större avvikelser i portföljens
avkastning jämfört med index.
Svenska fonder redovisar sedan ett antal år Tracking Error som nyckeltal. Det baseras på de
senaste 24 månadernas skillnader mot jämförelseindex och redovisas omräknat i årstakt.
Nedan visas exempel på Tracking Error.
Exempel: Tracking Error för några Sverige-fonder (% i årstakt)
Månadsvis november 2007 - oktober 2012
Fond
Nordea Sverigefond
SEB Sverigefond
Handelsbankens Sverigefond
Swedbank Robur Sverigefond
AMF Aktiefond Sverige
Länsförsäkringar Sverigefond
Lannebo Sverige
Enter Sverige
Catella Reavinstfond
Danske Invest Sverige
DNB Sverigefond
Tracking Error
4,1
2,8
3,1
3,8
3,1
3,7
6,4
5,0
3,5
6,5
3,3
Källa: Moneymate, egna beräkningar
Ett vanligt mönster när det gäller Sverigefonder är att ju större förvaltare, desto närmare index
måste man ligga, så de fyra storbankernas fonder har ofta lågt Tracking Error. Noterbart
denna period är att såväl Nordea som Robur har relativt höga Tracking Error mot tidigare
normalläge. Typiskt är även att vissa av de mindre förvaltarna tar ut svängarna mer jämfört
med index, t ex. Lannebo med 6,4 % och Danske Invest med 6,5 %
Tracking Error utgör riskmåttet för ett ofta använt mått på riskjusterad avkastning kallat
informationskvot. Det relaterar portföljens genomsnittliga avkastning i förhållande till index
(ibland kallat avvikelseavkastning) i förhållande till spridningen i denna skillnad som mäts
med Tracking Error. Tanken med detta mått är att det ska mäta hur effektiv förvaltaren har
varit genom att avvika från index: hur mycket har jag fått betalt per avvikande position? Helt
enkelt ett mått på förvaltarens skicklighet (eller, som sagt, tur).
Informationskvot är det helt dominerande måttet på riskjusterad avkastning på den
institutionella kapitalförvaltningsmarknaden. Där är det ofta det enda måttet på riskjusterad
avkastning som används.
Exempel: Informationskvot
Under en treårsperiod steg index med 8% per år (aritmetiskt medelvärde). Ett antal fonder
hade följande utveckling:
43
Fond
A
B
C
Avkastning
8,5
9,0
9,4
Tracking Error
2,5
5,6
8,4
Analysera hur väl fonderna har presterat utifrån informationskvot!
Svar: A: (8,5 - 8) / 2,5 = 0,20, B: (9,0-8)/5,6 = 0,18, Fond C: (9,4 - 8) / 8,4 = 0,17. Alltså var
fond A bäst, följd av fond B, medan fond C var sämst
7.6 Relevanta jämförelseindex
Vid användningen av måttet informationskvot är det av stor betydelse att man använder ett
relevant jämförelseindex. Jämförelseindexet ska bland annat ha följande egenskaper:



förvaltaren ska kunna investera i alla tillgångar i indexet
indexet ska avspegla portföljens investeringsinriktning
indexet ska på ett korrekt sätt mäta den avkastning som förvaltaren kan uppnå, vilket
bland annat innebär att det ska inkludera återinvesterade utdelningar
Här är det viktigt att känna till skillnaden mellan ett prisindex och ett avkastningsindex. Vid
beräkning av ett prisindex så ingår inte de utdelningar som bolagen ger. Det är bara
kursutvecklingen som man följer. Vid beräkning av ett avkastningsindex återinvesteras
utdelningarna, vilket gör att den typen av index är bättre, om man vill se vilken
totalavkastning man har fått.
När vi nu har definierat två typer av index, med eller utan utdelning, så finns det även olika
sätt att sätta ihop vikterna för de bolag som ingår i indexet. Praktiskt taget samtliga
jämförelseindex som används på marknaden baseras på respektive tillgångs andel av det totala
marknadsvärdet, s.k. marknadsvärdeviktat eller kapitalviktat index (d.v.s. vikten bestäms
av respektive bolags andel av det totala börsvärdet). De internationella indexen (se tabell
nedan) samt vissa svenska index, tillämpar sedan ett antal år även en justering av
marknadsvärdena i bolag, där en stor del av aktierna ägs av s.k. strategiska ägare, som inte
handlar aktivt med sitt aktieinnehav, t ex. svenska statens ägande i TeliaSonera (drygt 37%). I
sådana index väger således TeliaSonera väsentligt mindre än i ett index som inte justerar för
detta. Sådana index kallas friflödesjusterade eller på engelska free-float adjusted.
Det förekommer även i vissa fall andra sätt att beräkna vikterna i ett index, vid ett likaviktat
index har alla bolag samma indexvikt. Vid ett prisviktat index ingår aktierna utifrån kursen
på aktien. En aktie som handlas till kurs 200 kr har alltså en dubbelt så stor indexvikt, som
den aktie som handlas till 100 kr. Det samlade börsvärdet har ingen betydelse i någon av
dessa två typer av index.
Tabell: vanliga jämförelseindex för olika fondkategorier
Fondkategori
Global-, regionfonder
Sverigefond
Obligationsfond
Penningmarknadsfond
Blandfond
Hedgefond
Vanliga index
MSCI, FTSE
SIXPRX, OMXSB
OMRXBOND
OMRXTBILL
Sammanvägt index
OMRXTBILL
44
7.7 Rating av fonder
Ett hjälpmedel vid val av fonder inom en fondkategori är att studera fondbetyg. Det finns ett
antal olika fondbetyg avseende fonder på den svenska marknaden. Det mest spridda är
Morningstars fondbetyg, som beskrivs nedan.
Morningstar publicerar fondbetyg baserat på fondernas historiska utveckling. Fonderna delas
in i över 140 kategorier, t ex. ”Svensk aktiefond, små/medelstora bolag”, ”Latinamerika”,
”Räntefond, SEK penningmarknad” och ”Branschfond, Läkemedel”. Inom kategorierna
jämförs sedan varje fonds avkastning och risk, med alla liknande fonder i Europa.
Högsta betyg är 5, och det går till de 10 procent bästa fonderna i var och en av kategorierna.
Ratingen baseras på resultaten 3, 5 och 10 år bakåt och total rating är ett vägt snitt av de tre
delbetygen. I och med att betygen endast baseras på historisk avkastning och volatilitet är de
lätta att uppdatera, och detta sker månadsvis. Aktuella betyg återfinns på hemsidan
www.morningstar.se.
I första hand är Morningstars rating intressant för den som har bestämt sig för att spara i en
fond av en viss typ, och vill veta vilka fonder inom kategorin som har haft förvaltare som har
lyckats bättre än konkurrenterna. Den är inte någon köp- eller säljrekommendation, men om
man tror att det finns ett samband mellan historiska och framtida resultat kan Morningstars
rating ge viss vägledning.
8. Privatekonomi: hur välja portfölj i praktiken?
Hur kan du då använda dig av de kunskaper om ekonomi, som vi gått igenom när du ger råd
om placeringar? För det första krävs en grundläggande kartläggning av kundens situation för
att lära känna din kund. Du ska samla in uppgifter och analysera kundens ekonomiska
situation (inkomster, utgifter och förmögenhet), framtidsplaner och inställning till risk. Här
kommenteras var och en av dessa tre grundförutsättningar. Därefter redovisas exempel på
olika fondportföljer med olika risknivåer, som kan vara lämpliga för kunder med olika
förutsättningar. Att rådet ska vara lämpligt utifrån kundens individuella förutsättningar är ett
mycket viktigt krav som följer av lagen om värdepappersmarknaden. Även om du som
rådgivare många gånger inte personligen tar fram portföljförslaget, utan det genereras av ett
system, där förvaltarna räknat fram olika modellportföljer, behöver du säkerställa att råden
verkligen passar din kund. Mer om detta i delområde 3 Kundmöte, Etik och regelverk. Vidare
redovisas exempel på kort- och långsiktig fördelning mellan olika tillgångar och några
begrepp som förekommer i det sammanhanget. Slutligen beskrivs vad som kan hända i en
portfölj över tiden om marknaderna rör sig och en sätt att hantera sådana situationer.
8.1 Sparutrymme (löpande ekonomi)
En viktig del i kartläggningen, är att beräkna kundens sparutrymme. Det handlar om de
löpande inkomster och utgifter som hushållet har, motsvarande ett företags resultaträkning.
Bland inkomster finns löner (efter skatt), bostadsbidrag, barnbidrag, räntor och andra
kapitalinkomster, försäkringsersättningar m.m., vilket totalt brukar kallas för disponibel
inkomst. Bland utgifter finns boendekostnader (inklusive bolåneräntor och -amorteringar),
mat och alla andra löpande konsumtionsutgifter. Konsumentverket har gjort beräkningar på
vilka kostnader man har för att upprätthålla en rimlig levnadsstandard. Dessa beräkningar ska
du känna till och kan användas som referensram innan du har kundens verkliga kostnader.
45
Nettot av disponibel inkomst och konsumtionsutgifter anger det s.k. sparutrymmet. Om
sparutrymmet är negativt, är det en väldigt viktig varningssignal eftersom man lever över sina
ekonomiska förutsättningar (då kan man vara aktuell för TV-programmet Lyxfällan…). För
de flesta hushållen är dock sparutrymmet positivt. Det anger då vilket finansiellt utrymme
kunden har för att öka sitt egna kapital och därmed finansiera framtida investeringar (t ex. köp
av villa/bostadsrätt) eller andra större framtida utgifter såsom pension, genom att kunna
placera kapital på ett lämpligt sätt.
8.2 Nettoförmögenhet (tillgångar, skulder)
En annan viktig del i kartläggningen av din kund, är att beräkna kundens nettoförmögenhet.
Den har bland annat betydelse för när du bedömer lämplig risknivå för kunden. Även här kan
man jämföra analysen av den ekonomiska situationen för ett hushåll med motsvarande för ett
företag. Ett hushåll har tillgångar i form av boende, sparkonton, andra finansiella tillgångar,
pensionsrätter. Vidare har man skulder i form av bolån och eventuella andra lån. Det kan
beskrivas som ett hushålls balansräkning, där summa tillgångar minus summa skulder anger
hushållets egna kapital eller nettoförmögenhet.
8.3 Placeringshorisont och sparmål
Nästa steg är att kartlägga hushållets framtida planer och ambitioner. Vilka investeringar
planerar kunden? Köpa sommarhus, byta bostad eller spara för barnens framtid? Pension
behöver alla planera för: hur mycket och när? Vilka andra ändamål för sparandet finns det?
Det är vanligt att dela upp sparmålen i tre grupper; buffertsparande för oförutsedda utgifter,
målsparande och slutligen pensionssparande. Tidshorisonten för de olika sparmålen är helt
olika, och det har betydelse för vilken risknivå man ska välja på sina placeringar. Oförutsedda
utgifter kan dyka upp när som helst, så tidshorisonten är därför mycket kort när det gäller
buffertsparandet. För målsparandet beror det på vad målet är, om det t.ex. är att köpa en
segelbåt om 5 år, är tidshorisonten för placeringen 5 år. När det gäller pensionssparande beror
tidshorisonten på hur långt man har kvar till pensionen.
Tidshorisonten är en viktig del när det gäller att rekommendera rätt risknivå för kundens
placeringar. Ju längre tidshorisont, desto högre risk bör kunden kunna ta i sina placeringar.
Den högre risken bör ge en högre förväntad avkastning, som vi talat om tidigare.
Buffertsparandet innebär kort tidshorisont och ska därför placeras till låg risk och dessutom
lättillgängligt. Ett målsparande på 2-5 år bör ha medellåg risk och det ska även här vara lätt att
få tillgång till kapitalet om man hittar det objekt man söker. För pensionssparandet kan man ta
högre risk i början när det är långt kvar till pensionen. När pensionsåldern sedan närmar sig
bör man dra ner risken successivt.
När sparmålen och deras tidshorisont har kartlagts, kan du göra en sammanlagd bedömning
om nettoförmögenheten och sparutrymmet räcker till för hushållets framtida planer och
ambitioner. Ett alternativt sätt är att se till realismen i framtidsplanerna och beräkna vilken
avkastning som skulle krävas på hushållets finansiella tillgångar för att uppnå sparmålen. Det
kan nog många gånger visa sig att sparmålen inte kan realiseras med nuvarande förmögenhet
och löpande sparande, vilket innebär att något måste anpassas:



anpassa sparmålen efter vad pengarna kommer att räcka till
öka löpande sparande för att komma närmare sparmålen
ett tredje alternativ kommer att diskuteras i nästa avsnitt som behandlar förväntad
avkastning och risk i de finansiella placeringarna
46
8.4 Analys av kundens riskattityd (risktolerans, riskvilja, riskaversion)
Analysen du gjorde ovan när det gäller kundens sparutrymme, nettoförmögenhet, sparmål och
tidshorisont kan ses som kundens risktålighet, förmågan att bära risk. Nästa steg är att
bedöma kundens vilja att ta risk. Två av dina kunder kan ha exakt samma förutsättningar när
det gäller sparutrymme och nettoförmögenhet, men om du frågar dem om hur de ser på risk,
kan du få helt olika svar. Det som för den ene kan upplevas som en spännande chansning, kan
den andre uppleva som ett obehagligt osäkerhetsmoment. Analysen måste därför kompletteras
med en bedömning av den enskilda kundens risktolerans, viljan att ta risk. I de behovsanalys
underlag du arbetar med för kartläggningen finns olika typer av standardiserade frågor som du
är skyldig att få besvarade av kunden. Tänk på att även ställa ytterligare kompletterande
frågor om du känner att kunden är osäker och du har svårt att fastställa kundens verkliga vilja
att ta risk för att nå en realistisk avkastning.
Enligt den finansiella teorin ska varje placerares val av risk i portföljen (t ex var på Capital
Market Line man ska pricka in sin fördelning mellan riskfria placeringar och en global
indexportfölj av riskfyllda tillgångar) bestämmas utifrån något som kallas en nyttofunktion.
Det finns i portföljteorin många olika nyttofunktioner, men de har ofta det gemensamt att de
bygger på att ju rikare vi blir, desto mindre värderar vi en ytterligare ökning av
förmögenheten, s.k. avtagande marginalnytta.
Ett enkelt praktiskt exempel på det är om vi skulle erbjuda en kund ett s.k. "rättvist spel" (eng.
fair game). Kunden får välja mellan två alternativ, båda lika sannolika: 1. Tjäna 10 000 kr. 2
Förlora 10 000 kr. Skulle kunden acceptera detta rättvisa spel? Ja, kanske om det är en spelare
(det går trots allt många människor på kasinon och utsätter sig för spel som t o m har sämre
förutsättningar än detta). Men det är inte slutsatsen avseende kunders finansiella placeringar,
där antar man att den "normala" kunden inte skulle acceptera detta erbjudande, eftersom det
introducerar en risk utan att ge någon förväntad nettoavkastning. Ett möjligt sätt att mäta hur
ovillig kunden skulle vara till denna typ av spel är att ändra förutsättningarna och istället
uttrycka frågan enligt ett antal svarsalternativ, se exempel nedan.
Exempel: Fråga om riskattityd
Du erbjuds följande spel: Du har 50% risk att få betala 10 000 kr. Samtidigt har du 50% chans
att tjäna ett visst belopp. Hur stort måste det beloppet minst vara för att spelet ska vara
intressant, välj ett alternativ av följande!
1. 10 000 kr
2. 11 000 kr
3. 12 000 kr
4. 13 000 kr
Givet svaret på en sådan fråga kan man möjligen dra någon sorts slutsats om kundens
riskattityd, som rent teoretiskt skulle kunna översättas till en matematisk nyttofunktion. Den
som valde alternativ 1 kallas för en riskneutral placerare, som inte bryr sig om risken.
Kunder som svarar något av alternativ 2-4 har s.k. riskaversion, vilket innebär att de vill ha
betalt för att ta risk. Emellertid har denna enkla metod (och många andra metoder, t ex att
fråga kunden om risktagande i vardagssituationen) svagheten, att den kanske inte alls stämmer
när det gäller kundens faktiska ekonomiska ställning och inställningen till risken i de egna
finansiella placeringarna.
Andra alternativa sätt att få en bild av inställningen till risken i finansiella placeringar är
kundens tidigare agerande i olika situationer. Hur har portföljen sett ut i tidigare skeden,
47
särskilt i samband med svaga perioder på finansmarknaden, och hur har kunden dels upplevt
läget i sådana fall, dels agerat?
Problemet att klarlägga en kunds inställning till risk i sina finansiella placeringar, är som
framgår mycket svårt och det kan knappast hävdas att det finns någon enda sanning även i
detta fall. Det är förklaringen till att denna kartläggning ofta sker relativt schablonmässigt och
resulterar i relativt enkla och standardiserade portföljförslag, där risknivån framför allt
bestäms av placeringshorisonten, med eventuella individuella justeringar för kunder som t ex.
"inte vill förlora pengar" etc.
Ytterligare ett allvarligt problem i samband med placeringsrådgivning är att kunder har en
varierande riskattityd över tiden. Det finns rikliga tecken på att kunders riskattityd påverkas
av hur marknaderna har utvecklats. En intressant iakttagelse är att detta gäller inte bara
privatkunder, utan även professionella förvaltare. Man kan som exempel fundera på hur
kunders riskattityd var sommaren 2007, efter fyra år med stadiga börsuppgångar och historiskt
sett låg volatilitet. Risk var nog inte så uppmärksammat i det läget. Om man frågade samma
kunder vid årsskiftet 2008/2009 om deras inställning till risk, efter en börsnedgång på nästan
hälften och en kraftig uppgång i volatiliteten, så kan man fundera på hur inställningen till risk
hade förändrats - sannolikt markant till det mer negativa.
Ett sätt att förhålla sig till detta är att (1) att fokusera på rätt placeringshorisont, det var trots
allt inte alla kunder som skulle ta ut sina pengar vid årsskiftet 2008/2009, och de behövde
bara vänta i ett par år för att tjäna tillbaka en stor del av börsfallet. (2) Se till risk över lite
längre horisonter och hålla i minnet att lugna och volatila perioder kommer att avlösa
varandra, men att även volatiliteten på lång sikt tenderar att jämna ut sig, vilket talar för att
man kan satsa på att behålla en viss portföljfördelning hur marknaden än utvecklas (se vidare
avsnitt 8.7 nedan).
8.5 Empiriska resultat om risk och samvariation för olika fondkategorier
Hur kan då lämpliga portföljer se ut, givet placeringshorisonten och riskattityden? För att ge
ett exempel på det i form av olika marknadsindex (tänk fondkategorier) presenteras nedan
dels risken i olika typer av fonder mätt som årlig standardavvikelse under 60 månader t o m
oktober 2012, dels korrelationen mellan olika marknadsindex. Därefter presenteras exempel
på risken i olika portföljer av dessa marknadsindex, vilket då inkluderar effekten av
diversifiering. Portföljalternativen är utvalda för att passa olika risknivåer. En reservation som
är viktig i detta sammanhang, är att dessa exempel utgör en viss, speciell femårsperiod som
innehåller den värsta finanskrisen på 70 år samt en rejäl återhämtning, så det finns mycket
som talar för att kommande fem-tio år inte kommer att se likadana ut. Däremot tenderar
risknivåerna i olika tillgångsslag relativt varandra att ha ungefär samma förhållanden, vilket
talar för att rangordningen av portföljalternativ avseende risk kommer att vara ungefär
desamma om detta exempel skulle göras igen om fem år.
Standardavvikelse för olika marknadsindex (årstakt, %) nov 2007- okt 2012
Marknad
Svenska aktier
Globala aktier, utvecklade
Globala tillväxtmarknader
Globala aktier, utvecklade och tillväxt
Globala småbolag
Nordamerika
Europa
48
Standardavvikelse
21,9
12,3
20,5
12,8
16,1
12,4
15,4
Japan
BRIC
Svenska obligationer
Svenska korta räntor
14,4
24,4
3,3
0,5
Källa: Moneymate, egna beräkningar
För denna period kan vi konstatera att den mest diversifierade portföljen, globala aktier i
utvecklade marknader haft lägst risk, 12,3%, även om nordamerikanska aktier legat mycket
nära denna låga nivå med 12,4%. En vanlig variant för globalfonder är att ta med
tillväxtmarknader (MSCI All Country), vilket drar upp risken något, till 12,8%. Globala
tillväxtmarknader ligger väsentligt högre med 20,5%. En snävare portfölj med bara fyra
aktiemarknader - BRIC, Brasilien, Ryssland, Indien och Kina - ligger väsentligt högre med
24,4%.
En utvecklad regionmarknad som Europa ligger något högre, 15,4%. Svenska aktier brukar
ligga relativt högt och gör så även nu med 21,9%. Den svenska börsen är relativt koncentrerad
såväl bolags- som branschmässigt. Svenska obligationer ligger väsentligt lägre än alla
aktieindex på 3,3% och svenska korta räntor på mycket obetydliga 0,5%.
Tabell: Korrelation mellan olika marknadsindex, nov 2007-okt 2012
Par av marknader
Sverige - Global
Sverige - Europa
Sverige - Nordamerika
Sverige - Globala tillväxtmarknader
Sverige - Japan
Globala utvecklade - Globala tillväxtm.
Globala utvecklade - obligationer
Sverige - obligationer
Korrelation
0,76
0,85
0,61
0,82
0,33
0,80
– 0,37
– 0,46
Källa: Moneymate
Som väntat har svenska aktier högst korrelation med europeiska, 0,85, men även mot globala
tillväxtmarknader har det under denna period legat relativt högt med 0,82. Generellt har
tillväxtmarknadernas samvariation med utvecklade marknader tenderat att öka i takt med
ökade internationella placeringar i dessa marknader. Korrelationen mellan Sverige och andra
utvecklade marknader är klart lägre, som Nordamerika 0,61 och Japan 0,33. Sammantaget är
korrelationen mellan Sverige och globala utvecklade marknader lite av ett genomsnitt med
0,76. Innebörden av dessa relativt höga korrelationstal är att utrymmet för diversifiering
mellan olika aktiemarknader blir relativt begränsat. Däremot har korrelationen mellan
aktiemarknader och räntemarknaderna varit klart negativ, vilket innebär att ett ränteinslag i en
portfölj har stor effekt i form av lägre risk.
Sett till länderfonder jämfört med regionfonder finns ett mycket bra och enkelt exempel i
form av BRIC-fonder, som består av aktier i Brasilien, Ryssland, Indien och Kina (China).
Volatiliteten i respektive landindex, korrelationerna samt risken i en sammanvägd portfölj
redovisas i tabellen nedan.
Tabell: Risk i BRIC-länderna, korrelationer samt risk i en BRIC-portfölj nov 2007-okt 2012
Marknad
Brasilien
Standardavvikelse
27,4
49
Ryssland
Indien
Kina
BRIC-portfölj
Marknader
Korrelation Brasilien-Ryssland
Korrelation Brasilien-Indien
Korrelation Brasilien-Kina
Korrelation Ryssland-Indien
Korrelation Ryssland-Kina
Korrelation Indien-Kina
33,5
31,7
25,5
24,4
Korrelation
0,80
0,67
0,66
0,56
0,48
0,66
Källa: Moneymate
8.6 Fondportföljer för olika risknivåer
Baserat på de empiriska resultaten för risk och samvariation i föregående avsnitt, presenteras
här ett exempel på olika modellportföljer av ett relativt enkelt slag, men som till stor del
motsvaras av de modellportföljer, blandfonder eller fondandelsfonder som förekommer på
marknaden. De bygger således helt och hållet på den historiska risken och samvariationen
under en aktuell femårsperiod. För att kunna uttala sig någorlunda vettigt om den framtida
förväntade spridningen, krävs även att vi har en uppfattning om framtida förväntad
avkastning, och i enlighet med de teoretiska resonemangen i tidigare kapitel bygger dessa på
att placerare har riskaversion och förväntar sig en högre avkastning från tillgångar med högre
risk. Ett exempel på detta presenteras nedan.
Tabell: Rimlig förväntad årlig (aritmetisk) avkastning på olika tillgångar
Tillgång
Globala aktier (utvecklade marknader)
Tillväxtmarknader aktier
Svenska aktier
Svenska obligationer
Förväntad avkastning
6,0
7,0
6,5
2,0
Enligt portföljteorin ovan (Markowitz) borde portföljsammansättningen bestämmas av en s.k.
optimering, som matematiskt beräknar exakt portföljandel för olika tillgångar. Det går att
göra, men här har vi förenklat processen och väljer en schablonmässig fördelning mellan de
olika aktietillgångarna på 60% Globala utvecklade aktier, 20% Globala tillväxtmarknadsaktier
och 20% Svenska aktier. Dessutom fördelas ränteportföljen på hälften obligationer och
hälften kort ränta. Det resulterar i följande exempel på fondportföljer med olika risknivåer
som motsvarar vanliga modellportföljer.
Tabell: Exempel på fondportföljer med olika risknivå och förväntad avkastning(andel, %)
Portfölj
Låg risk
Försiktig
Balanserad
Offensiv
Högrisk
Global
0
15
30
45
60
Tillväxt
0
5
10
15
20
Sverige
0
5
10
15
20
Sverige ränta
100
75
50
25
0
Tabell: Risk mätt som standardavvikelse och risk för negativ avkastning på fondportföljer (%)
50
Portfölj
Låg risk
Försiktig
Balanserad
Offensiv
Högrisk
Förväntad
avkastning
2,0
3,1
4,2
5,2
6,3
Standardavvikelse
1,7
3,3
7,0
10,9
14,7
Förlustrisk,
ett år
12,0
17,6
27,7
31,6
33,4
Exempel
plac.horisont (år)
1
2-3
4-6
7-9
10-
Vi kan notera att på en så kort horisont som ett år, är det relativt stor risk att förlora pengar
även för blandportföljerna offensiv och balanserad. En väsentligt lägre förlustrisk uppnås först
vid Försiktig. Observera även att för den rena lågriskportföljen är förlustrisken på ett års sikt
hela 12%, vilket hänger samman med det låga ränteläget och därmed låg förväntad
avkastning. Utifrån kundens placeringshorisont kan man sikta mot en lämplig risknivå i
portföljen. Eventuellt kan du som rådgivare även justera portföljen för kundens mer specifika
riskattityd, genom att diskutera t ex risken att förlora pengar även på en kortare horisont än
placeringshorisonten.
Det finns alternativa (och mer arbetskrävande) sätt att angripa placeringsrådgivningen. Om t
ex. en kund har ett antal olika sparmål med olika placeringshorisonter, kan en möjlig strategi
vara att försöka matcha olika delportföljer för att på bästa sätt uppnå respektive sparmål. Detta
angreppssätt kan möjligen anses stå i strid med lagen om investeringsrådgivning som specifikt
anger att hänsyn i första hand ska tas till placeringsportföljens totala risk, kundens förmåga att
bära risken. Men likafullt är detta ett väletablerat sätt för institutioner, att matcha placeringar
mot väntade utgifter med olika placeringshorisonter.
8.7 Strategisk och taktisk allokering samt rebalansering
Det avsnitt syftar till att du ska förstå varför den strategiska allokeringen normalt anses vara
viktigare än den taktiska allokeringen för en portföljs långsiktiga avkastning. Därutöver att
förstå på vilket sätt taktiska allokeringsbeslut ger upphov till Tracking Error.
När en kund väl har bestämt sig för en viss portfölj, som passar för placeringshorisonten och
riskattityden, så kallar man ofta portföljens fördelning mellan olika tillgångsslag för en
strategisk allokering. Det är den genomsnittliga fördelningen mellan tillgångarna som ska
tillämpas långsiktigt (med planerade justeringar varefter placeringshorisonten närmar sig,
jämför generationsfonderna). Den strategiska allokeringen är det viktigaste beslutet en kund
gör och är avgörande för portföljens långsiktiga avkastning.
Vid olika tillfällen kan det uppstå situationer när marknadernas förväntade avkastning på en
kortare horisont, säg ett år, inte motsvarar den långsiktiga förväntade avkastningen. Då kan
det vara aktuellt att tillfälligt avvika från den genomsnittliga långsiktiga strategiska
allokeringen. Ett exempel kan vara en kund med en balanserad portfölj (50% aktier) som har
en negativ tro på aktiemarknaden på ett års sikt. Då kan det vara motiverat att t ex. sänka
aktieandelen från 50% till säg 25% i syfte att (relativt sett) uppnå en bättre avkastning än den
strategiska allokeringen. Sådana tillfälliga avvikelser i tillgångsfördelningen kallas för taktisk
allokering. Detta är ju även vad som t ex. sker i blandfonder, där fondförvaltaren över- eller
under allokerar tillgångarna i förhållande till den normala tillgångsfördelningen. Att en
förvaltare avviker kortsiktigt från sina normalvikter kallas att man tar en aktiv risk, vilket
mäts med Tracking Error (se 7.4).
51
En varning kan vara befogad när det gäller taktisk allokering: det är svårt! Även
professionella förvaltare har stora svårigheter att förutse den kortsiktiga utvecklingen på
marknaden. Och när det gäller privatkunder finns det rikligt med faktaunderlag som talar för
att de är systematiskt dåliga på att förutse marknaden (t ex i form av flöden till och från
aktiefonder).
Mot den bakgrunden finns det ett välgrundat sätt att ge råd, som inte bygger på en uppfattning
om marknaderna på kort sikt, utan som bygger på en sund princip för portföljens risknivå (jfr
avsnitt 8.4 ovan). Det är att rekommendera kunder att med regelbundna mellanrum återställa
den ursprungliga risknivån i portföljen om marknadsutvecklingen har medfört en förändring
av denna. En sådan åtgärd kallas ofta för rebalansering. Eftersom aktiemarknaden ofta
uppvisar trender över ett till två år har en sådan strategi dels den viktiga fördelen att
portföljens risknivå hålls någorlunda konstant över tiden, dels kan den i vissa situationer ha en
ytterligare fördel att man tenderar att köpa aktier efter ett kraftigt börsfall respektive sälja
aktier efter en kraftig börsuppgång. Det låter väl som en ganska vettig strategi oavsett vad
man tror om framtiden?
Exempel rebalansering 2008-2009
Här redovisas ett enkelt exempel på vad som kan hända vid t ex. en årlig rebalansering. Anta
att en kund i början av 2008 hade en portfölj med hälften svenska aktier och hälften svenska
obligationer. För enkelhets skull antas portföljen ha bestått av 50 kr i vardera tillgången.
Under 2008 föll aktierna med 39,1%, medan obligationerna steg med 11,7%. I slutet av året
såg portföljen med andra ord ut enligt följande: Aktier 50 * (1-0,391) = 30,5 kr, räntor 50 *
1,117 = 55,9 kr, totalt 86,3 kr. Fördelningen var nu 35,3% aktier och 64,7% räntor. Vad bör
man göra i detta läge? Förslag: återställ risken till den ursprungliga fördelningen med hälften i
vardera tillgången. Resultat: aktier 43,15 kr och räntor 43,15 kr.
Under 2009 steg svenska aktier med 53,3% och svenska räntor med 3,0%. Portföljen steg
därmed till 43,15 * 1,533 + 43,15 * 1,03 = 110,6 kr, eller med 28,2%. Utan re balansering
hade den bara stigit till 30,5 * 1,533 + 55,9 * 1,03 = 104,3, eller med 20,7%. Skillnaden i
slutvärde utgjorde 110,6 / 104,2 - 1 = 6,1%. Rebalansering kan alltså vara lönsamt. Frågan är
emellertid hur många placerare som hade modet att öka på aktieportföljen vid årsskiftet
2008/2009 (apropå varierande riskaversion, jfr avsnitt 8.4 ovan).
Kommentar Privatekonomi
För all er som arbetar som rådgivare, är det mycket viktigt att förstå vad lagen om
värdepappersmarknaden innebär i din roll som rådgivare. Detta behandlas i delområde 3
Kundmöte, etik och regelverk.
9. Avslutning
Detta kompendium utgör ett kort sammandrag av väsentliga begrepp och samband inom
området Ekonomi i SwedSecs kunskapskrav för rådgivare. Syftet med kompendiet är att det
ska ge dig en grundförståelse som du har nytta av i ditt arbete och inför SwedSectestet. I syfte
att säkerställa och kontrollera din inlärning rekommenderar vi dig att komplettera studiet av
kompendiet, med att gå igenom övriga komponenter i utbildningens studieplan i
Rådgivarportalen. Där finns bland annat s.k. Träningspass som innebär praktiska frågor och
övningar på innehåller, diagnostester med mera. Lycka till! Önskar i på Finanskompetens
52
Ordlista
Begrepp som i texten markerats med fetstil eller i rubriker finns i denna ordlista med en kort
förklaring av vad de betyder. Ord i Betydelse-kolumnen som börjar med versaler förekommer
även som Begrepp.
Begrepp
Aktiv risk
Alfa
Alternativa
Investeringsstrategier (AIS)
Aritmetiskt medelvärde
Avkastningskrav
Avkastningskurvan
Avtagande marginalnytta
Avvikelseavkastning
Balansräkning
Belåning
Beta
BIS
BNP
Bruttonationalprodukt
Bytesbalans
Capital Asset Pricing Model
Capital Market Line
CAPM
CML
Deflation
Direktavkastning
Betydelse
En portföljs benägenhet att avvika från sitt index. Se även
Tracking Error
I en Regression ett mått på hur en akties specifika rörelser
avkastat i genomsnitt
Placering i andra tillgångar än sedvanliga värdepapper.
Exempel hedgefonder, råvaror, fastigheter m.m.
Summan av ett antal observationer dividerat med antalet
Den förväntade avkastning som placerare kräver givet
risken i en placering, se även Diskonteringsränta
Ett diagram med löptid på x-axeln och marknadsränta på
y-axeln. Det beskriver strukturen på marknadsräntor på
olika löptider för en viss emittent, t ex svenska staten
Ett vanligt antagande om ökad förmögenhet: ju rikare man
blir, desto mindre nytta har man av en ytterligare ökning
av förmögenheten
Skillnad mellan en portföljs avkastning och index d: o
En sammanställning av tillgångar, skulder och eget kapital
Att genom att låna öka sin portfölj utöver
nettoförmögenheten
I en Regression ett mått på en akties benägenhet att följa
med marknaden, även kallat Marknadsrisk eller
Systematisk risk.
Bank for International Settlements, samarbetsorganisation
för centralbanker baserad i Basel, Schweiz
Se Bruttonationalprodukt
Summan av värdet av alla varor och tjänster som
produceras i ett land under en viss period (år, kvartal)
Nettot av export minus import av varor och tjänster samt
netto kapitalavkastning för ett land. Ett mått på det
finansiella nettot gentemot omvärlden.
En modell avseende portföljval och värdering. Portföljval
bör ske i form av en blandning av riskfri tillgång och en
global marknadsportfölj av riskfyllda tillgångar. Värdering
bör baseras på marknadsrisk (beta-värde).
Ett diagram i CAPM som beskriver de effektiva
blandportföljerna/belånade portföljerna med riskfri
tillgång och global marknadsportfölj.
Se Capital Asset Pricing Model
Se Capital Market Line
Fallande genomsnittliga priser
Utdelning dividerad med aktuell kurs
53
Diskonteringsinstrument
Diskonteringsmodellen
Diskonteringsränta
Disponibel inkomst
Diversifiering
Dividend Discount Model
Duration
ECB
Effektiv front
Effektiv årsränta
Effektiva portföljer
Efterfrågechock
Eget kapital
Ekonomisk politik
Ekonomisk ställning
Enkel årsränta
Epsilon
Faktisk avkastning
Fast växelkurs
Finansiell stabilitet
Fondbetyg
Fondrating
Instrument utan specifik räntebetalning, räntan erhålls
genom att betala en underkurs jämfört med nominellt
belopp
Se Dividend Discount Model
Den ränta som används för att räkna om ett Framtida värde
till Nuvärde. Beräkningen sker genom att det framtida
värdet divideras med ett plus diskonteringsräntan,
Vad ett hushåll får ut i lön efter skatt, kapitalinkomster,
försäkringsersättningar m.m.?
Riskspridning, kan bidra till lägre risk i en portfölj om man
väljer tillgångar som har en Korrelation lägre än +1
En vanlig metod för att beräkna Motiverad kurs för aktier
som bygger på diskontering av förväntade framtida
utdelningar
Ett mått på den genomsnittliga löptiden på framtida
kassaflöden för en Obligation eller ränteportfölj. Vikten
bestäms av andelen av obligationens eller portföljens
nuvärde.
Europeiska Centralbanken, centralbank för euro-länderna
med säte i Frankfurt, Tyskland
Ett diagram som beskriver Effektiva portföljers förväntade
risk och avkastning
Ett mått på årsränta som vid fler än en räntebetalning per
år tar hänsyn till ränta-på-ränta-effekt, och därmed i så fall
blir högre en motsvarande Enkel årsränta
Enligt portföljteorin de portföljer som för en given
risknivå har högst förväntad avkastning, eller för en given
förväntad avkastning har lägst risk.
En kraftig minskning av efterfrågan i en ekonomi
(exempel hösten 2008, då svensk export rasade)
För ett företag lika med summa tillgångar minus summa
skulder.
Politik som påverkar ekonomins utveckling. Brukar delas
in i Penningpolitik respektive Finanspolitik
En översiktlig bild av en kunds förmögenhet, disponibla
inkomster, konsumtionsutgifter och sparande.
Den nominella årliga räntesatsen på ett lån (oavsett om den
betalas i delar flera gånger per år). Jfr Effektiv årsränta.
I en Regression avvikelsen mellan observationer (punkter i
diagrammet) och trendlinjen. Spridning i dessa utgör
måttet på Specifik risk.
Realiserad historisk avkastning. Jfr Förväntad avkastning.
En valutapolitik som innebär att centralbanken har
fastställt ett visst förhållande mellan den egna valutan och
någon annan valuta eller korg av valutor. Tillämpades i
Sverige fram till 1992.
En rapport som regelbundet publiceras av Riksbanken om
den svenska finansmarknadens stabilitet.
Sätt att utvärdera fonder. Vanligaste heter Morningstar
Se fondbetyg.
54
Framtida värde
Free-float adjusted index
Friflödesjusterat index
Förlagslån
Förmögenhet
Försörjningsbalans
Förväntad avkastning
Geometriskt medelvärde
High Yield
IMF
Inflation
Inflationsmålet
Informationskvot
Investment grade
Jensens alfa
Jämförelseindex
Kapitalviktat index
Konstant tillväxt
Konsumentprisindex
Konsumtionsutgifter
Korrelation (-koefficient)
KPI
Kreditrisk
Ett kassaflöde som - säkert eller osäkert - kommer att falla
ut vid ett framtida tillfälle.
Ett index som vid sammanvägning tar hänsyn till att vissa
bolag har strategiska ägare (t ex svenska staten), vars
aktier inte är tillgängliga för andra placerare.
Se Free-float adjusted index
Ett räntepapper som är efterställt Obligation vid en
emittents konkurs, och som därmed har sämre
kreditvärdighet.
Nettot av totala tillgångar minus skulder.
En tabell över komponenterna i Bruttonationalprodukten
En rimlig uppskattning av en genomsnittlig förväntad
framtida avkastning givet risken i en placering och
används som Diskonteringsränta vid en värdering av
finansiella tillgångar.
Vid beräkning av avkastning över flera perioder: ett plus
den årliga avkastningen varje period multipliceras, vilket
ger ett plus total avkastning (=Slutvärdefaktor).
Geometriskt medelvärde erhålls genom att ta roten ur
Slutvärdefaktorn, vilken rot bestäms av antalet perioder.
En vanlig beteckning för fonder som placerar i
företagsobligationer med Speculative grade.
Internationella valutafonden, organisation som stödjer
länder med betalningsproblem, baserad i Washington, DC,
USA
En uppgång i den allmänna prisnivån i ett land
Riksbankens mål för penningpolitiken: uppgången i
Konsumentprisindex ska ligga på 2 % +/- 1 %
Ett mått på riskjusterad avkastning, som beräknas som
meravkastning mot index dividerat med portföljens
Tracking Error.
Obligationer med god kreditvärdighet, lägst kreditbetyg
BBB eller motsvarande.
Ett mått på riskjusterad avkastning som bygger på CAPM.
Anger huruvida en portföljs Specifika risk har haft positiv
eller negativ avkastning.
Ett marknadsindex som tjänar som jämförelsenorm för en
portföljs utveckling
Ett marknadsindex där aktiernas vikter bestäms av andelen
av det totala börsvärdet
En variant av Dividend discount model som bygger på ett
antagande om konstant årlig tillväxt i framtiden
Ett mått på den genomsnittliga prisnivån på alla varor och
tjänster som konsumeras i ett land
Löpande utgifter för levnadskostnader
Mått på i vilken utsträckning två tillgångar samvarierar.
Kan som lägst vara -1, som högst +1
Se Konsumentprisindex.
Risk att en emittent av räntepapper inte kan betala räntor
eller lånebelopp.
55
Kupong
Kvalitativ analys
Libor
Likaviktat index
Likviditetsrisk
Marknadsmodellen
Marknadsrisk
Marknadsränta
Marknadsvärdeviktat index
Markowitz, Harry
Modern portföljteori
Morningstar
Motiverad kurs
Nettoförmögenhet
Nollkupongobligation
Nominell ränta
Normalfördelning
Nuvärde
Nyttofunktion
Obligation
OECD
Offentlig konsumtion
Omvänd repa
Operativ risk
Årlig räntebetalning i procent av nominellt belopp på en
Obligation.
Vid utvärdering av fonder: en analys en förvaltares
förmåga att uppnå goda framtida resultat baserat på
faktorer som personal, filosofi, process etc.
London inter-bank offered rate. Marknadsränta för bankers
lån till varandra.
Ett index där varje aktie har lika stor vikt.
Risken att man inte kan avyttra ett innehav utan att
påverka marknadspriset negativt.
En modell som mäter sambandet mellan en aktie eller
portfölj och hela marknaden. Det sker i form av en
statistisk teknik kallad Regression.
Kan tyvärr betyda två saker: 1. Mått på total volatilitet på
en tillgång i form av Standardavvikelse, 2. Mått på en
tillgångs benägenhet att följa med marknaden i form av
beta-värde.
För räntepapper den noteringsränta som används som
Diskonteringsränta vid beräkning av priset på
räntepapperet.
Se Kapitalviktat index.
Ekonom som bidrog till utvecklingen av Modern
portföljteori och som delade Riksbankens pris till Alfred
Nobels minne 1990.
En modell för att analysera förväntad avkastning och risk
för olika portföljer av riskfyllda tillgångar.
Det vanligaste Fondbetyget på den svenska
fondmarknaden.
Resultatet av en värdering av en aktie enligt t ex Dividend
Discount Model eller med P/E-tals-värdering
Kundens egna kapital (tillgångar minus skulder)
En obligation utan årliga räntebetalningar
En ränta som inte tar hänsyn till inflation
En sannolikhetsfördelning som är mycket vanlig i naturen
och som ofta antas gälla för spridningen i avkastning på
aktiemarknaden.
Det diskonterade värdet av ett Framtida värde.
En matematisk formulering av placerares inställning till
förväntad avkastning och risk
Ett räntepapper med ursprunglig löptid över ett år, normalt
med årlig räntebetalning (Kupong).
Organization for Economic Cooperation and
Development, baserad i Paris, samarbetsorganisation för
utvecklade länder
Statens, kommuners och landstings löpande utgifter för bl.
a rättsväsende, försvar, sjukvård, skola och forskning
En åtgärd Riksbanken kan vidta för att dra in likviditet
från banksystemet. Jfr Repa.
Risk att det blir fel i värdepappersaffärer till följd av t ex
systemfel eller mänskliga fel
56
Optimering
P/E-tal
Penningmarknadsinstrument
Penningpolitik
Penningpolitiskt mål
Placeringshorisont
Prisviktat index
Realränta
Re balansering
Regression
Repa
Reporänta
Repurchase agreement
Resultaträkning
Riksgäldskontoret
Riskaversion
Riskfri ränta
Riskjusterad avkastning
Riskneutral placerare
Riskpremie
Risktolerans
Riskvilja
Räntebana
En matematisk metod att beräkna olika Effektiva portföljer
givet förväntad avkastning och risk.
Price/Earning ratio, förhållandet mellan en akties kurs och
vinst per aktie
Ränteinstrument med löptid på högst ett år. Jfr
Diskonteringsinstrument
Riksbankens politik för att styra räntan, penningtillgången
och därmed indirekt inflationen
Se Inflationsmålet
Givet ett visst sparmål, hur länge ska sparandet vara
placerat?
Ett index där varje akties vikt bestäms av aktiekursen.
Nominell ränta justerad för inflationens effekt.
Åtgärd för att efter marknadsrörelser återställa en
ursprunglig fördelning mellan olika tillgångar i en portfölj.
En statistisk metod som används i Marknadsmodellen för
att mäta det systematiska sambandet mellan en aktie eller
portfölj och hela marknaden.
Se Repurchase agreement.
Riksbankens styrränta som avses påverka de korta
marknadsräntorna och därmed bl. a bolåneräntor och andra
räntor i ekonomin
Avtal om återköp. Riksbankens regelbundna
veckotransaktioner där man erbjuder sig att köpa
obligationer från bankerna med ett avtal om att bankerna
ska återköpa dessa om en eller två veckor. Riksbankens
metod för att styra likviditeten i banksystemet.
Ett företags netto av intäkter minus kostnader
En statlig myndighet som bl. a ansvarar för finansieringen
av statens budgetunderskott och förvaltningen av
statsskulden.
Motvilja mot att ta risk.
Ett viktigt begrepp i finansiell ekonomi. Utgör ofta
utgångspunkten för att fastställ en rimlig Riskpremie för
olika riskfyllda tillgångar.
Mått vid utvärdering av portföljer som justerar total
avkastning med olika riskmått. Syftar till att identifiera
skickliga (eller turliga) förvaltare till skillnad från dem
som uppnått hög avkastning endast tack vare hög risk.
En placerare som inte kräver någon Riskpremie för att ta
risker.
Den meravkastning utöver Riskfri ränta som placerare
borde kräva givet en placerings risk
Jfr Riskaversion. Ju större Riskaversion, desto mindre
risktolerans.
Jfr Risktolerans.
Sedan 2007 en av Riksbanken regelbundet publicerad
prognos för Reporäntans utveckling under de kommande
tre åren.
57
Ränterisk
Rörlig växelkurs
Samvariation
Security Market Line
Separationsteorin
Sharpe, William
Sharpe-kvot
Slutvärde
Slutvärdefaktor
SML
Sparmål
Sparutrymme
Specifik risk
Speculative grade
Stabiliseringspolitik
Standardavvikelse
Startvärde
Stibor
Strategisk allokering
Styrränta
Effekten på ett räntepappers pris i procent av en förändring
i marknadsräntan (oftast mätt med en uppgång på en
procentenhet).
En valutapolitik som innebär att centralbanken inte har
något mål för växelkursen utan låter marknaden bestämma
denna. Tillämpas i Sverige sedan 1992.
Ett mått på i vilken utsträckning två tillgångar rör sig åt
samma eller olika håll. Jfr Korrelation.
I CAPM, ett diagram som beskriver sambandet mellan
Beta och Förväntad avkastning för aktier och portföljer.
Teori som innebär att en placerare som enda riskfylld
tillgång ska välja en s.k. Tangentportfölj och sedan
anpassa risken genom lämpligt inslag av riskfri tillgång. M
a o ska man separera valet av aktieportfölj från valet av
risknivå.
En av de tongivande ekonomerna bakom CAPM, var med
och delade Riksbankens pris till Alfred Nobels minne
1990. Även känd för Sharpe-kvot.
Ett mått på riskjusterad avkastning som beräknas genom
att ta realiserad riskpremie dividerad med total risk mätt
som standardavvikelse.
Vad en placerings värde blir i slutet av en
placeringshorisont givet Startvärde och en förväntad
avkastning under perioden.
Slutvärde dividerat med Startvärde
Se Security Market Line
Olika ändamål som ett sparande ska uppfylla, t ex
semesterresa, köp av bostad, pension etc.
En analys av kundens löpande intäkter och utgifter leder
fram till om det finns utrymme för sparande och
placeringar
Den del av en akties rörelser som inte förklaras av
marknadens rörelser.
Räntepapper med sämre kreditvärdighet, kreditbetyg BB
eller lägre.
Ekonomisk-politiska åtgärder med syfte att stabilisera
ekonomisk tillväxt och inflation
Det vanligaste måttet på Volatilitet eller spridning i utfall.
Beräknas som kvadratroten ur den genomsnittliga
kvadraten på avvikelser från medelvärdet.
Ett belopp som placeras i början av en period. Jfr
Slutvärde.
Stockholm inter-bank offered rate, räntan för korta lån
mellan banker i Sverige.
Långsiktig genomsnittlig sammansättning av olika
tillgångar i en portfölj
En centralbanks annonserade ränta som via t ex Repor
används för att påverka korta marknadsräntor. Jfr
Reporänta.
58
Systematisk risk
Taktisk allokering
Tangentportföljen
Tillväxt
Totalt sparande
Tracking Error
Transfereringar
Utbudschock
Varians
Volatilitet
Värderingslinjen för
värdepapper
Värderingsmodell
Den del av en akties eller portföljs risk som kan förklaras
av följsamhet med marknadens rörelser. Mäts med Betavärde och kallas ofta Marknadsrisk.
Kort- eller medelfristiga avvikelser från Strategisk
allokering baserad på en bedömning av aktuella
marknadstendenser.
En speciell portfölj av riskfyllda tillgångar som i
kombination med riskfri tillgång har en högre förväntad
riskjusterad avkastning än alla andra effektiva riskfyllda
portföljer. Jfr Effektiva fronten.
Ökning av Bruttonationalprodukten mätt i volym (fasta
priser)
Disponibelinkomst minus konsumtionsutgifter
Ett mått på i vilken utsträckning en portfölj avviker från
sitt jämförelseindex. Mäts genom att beräkna en
standardavvikelse avseende spridningen i skillnaden
mellan portföljen och index.
Offentliga utgifter i form av bidrag och subventioner till
hushåll och företag.
En händelse som kraftigt påverkar utbudet (och därmed
priset) på någon varugrupp, t ex i form av livsmedel vid
missväxt
Det grundläggande spridningsmåttet, vars kvadratrot är
Standardavvikelse.
Ett allmänt begrepp för marknadsrörelser som vanligen
mäts med Standardavvikelse.
Se Security Market Line.
Exempel CAPM. En modell som har ett konkret förslag till
hur man ska bestämma Avkastningskrav på olika
riskfyllda tillgångar.
59