Mer trigonometri

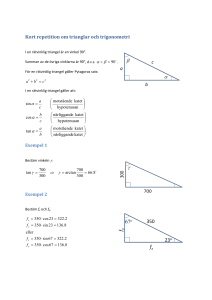
Sidor i boken
35-36
Mer trigonometri
Detta bör du kunna utantill
Figur 1:
Triangeln till vänster är en halv liksidig triangel. Varje triangel med vinklarna 30◦ , 60◦ , 90◦ är en
halv liksidig triangel. Hypotenusan är lika med den liksidiga triangelns sida. Den korta kateten är
förstås hälften av hypotenusan. Den längsta kateten är lika med höjden i den liksidiga triangeln.
Dess längd kan vi bestämma med hjälp av Pythagoras sats. Vi antar att den är x
s2 −
Håkan Strömberg
s2
=
s2
4
=
x
=
x
=
x
=
x
=
x
=
s 2
2
x2
r
+ x2
s2
s2 −
s 4
1
s2 1 −
4
r
4·1 1
−
s
4
r 4
3
s
√4
s 3
2
1
KTH STH
Blandar vi nu in trigonometri får vi följande samband som alla är viktiga att kunna utantill:
s
2
cos 60◦ =
s
√
s 3
2
=
1
2
√
3
2
√
√
s 3
3
◦
2
=
sin 60 =
s
2
s
1
sin 30◦ = 2 =
s
2
√
√
s 3
s 3 2 √
· = 3
tan 60◦ = 2s =
2
s
2
cos 30◦ =
tan 30◦ =
s
2
√
s 3
2
s
=
=
2
s
1
· √ = √
2 s 3
3
Vänder vi oss nu mot triangeln till höger ser vi att det är en halv kvadrat. Alla trianglar med vinklarna
45◦ , 45◦ , 90◦ är just halva kvadrater. Om den ena kateten är s så måste förstås även den andra vara
lika lång. Hypotenusan, lika med kvadratens diagonal, kan vi bestämma med Pythagoras sats. Vi
antar att den är x:
x2
=
s2 + s2
x2
√
x2
=
2s2
√
2s2
√
s 2
=
x =
Blandar vi nu in trigonometri får vi följande samband som är viktiga att kunna utantill:
s
1
cos 45◦ = √ = √
s 2
2
s
1
sin 45◦ = √ = √
s 2
2
tan 45◦ =
Håkan Strömberg
2
1
=1
1
KTH STH
Problem 1. Hur högt är Eiffeltornet? Sträckan BC = 150 m. ∠ABC = 63.4◦ .
Lösning: Vinkel och närliggande katet givna. Motstående katet efterfrågas.
tan v =
motstående
närliggande
Antag motstående katet är x m.
x
150
150 · tan 63.4◦
tan 63.4◦
=
x
=
x
≈ 300
Svar: 300 m
Problem 2. I takkonstruktionen är CM = 2.52 m och AB = 12.46 m Beräkna takvinkeln ∠BAC.
Lösning: Eftersom båda takvinklarna är v handlar det om en likbent triangel. Höjden delar triangeln i två rätvinkliga trianglar där motstående och närliggande katet är givna. Vinkeln v efterfrågas
tan v =
motstående
närliggande
ger
tan v
=
v
=
v ≈
2.52
12.46
2
arctan
2 · 2.52
12.46
22◦
Svar: 22◦
Problem 3. Beräkna vinkeln ∠CAB
Håkan Strömberg
3
KTH STH
Lösning: ∠CAB ska bestämmas. Vi startar med att bestämma ∠ACD som vi antar är v◦ .
120
240
1
v = arctan
2
◦
v ≈ 26.57
tan v
=
Vi kan nu bestämma
∠ACB = 180◦ − ∠ACD = 180◦ − 26.57◦ = 153.43◦
I nästa steg bestämmer vi ∠ABD som vi antar är u◦
tan u
=
u
=
120
240 + 180
120
arctan
420
15.94◦
u ≈
∠CAB får vi nu genom
∠CAB = 180◦ − 153.43◦ − 15.94◦ = 10.63◦
Svar: 10.6◦
Problem 4. För att en 9.0 m lång stege ska stå säkert när den reses mot en vägg får vinkeln
med markplanet ej understiga 64◦ och ej överstiga 78◦ . Bestäm stegens kortaste respektive längsta
avstånd till väggen, då den är i säkert läge.
Lösning:
Vi har två trianglar där vi ska bestämma den närliggande katet. I △ABC är ∠ABC = 78◦ . Den
eftersökta kateten betecknad med x ger
cos 78◦
=
x
=
x ≈
x
9
9 cos 78◦
1.871
I △DEF är ∠DEF = 64◦ Den eftersökta kateten betecknad med y ger
cos 64◦
=
x
=
x ≈
x
9
9 cos 64◦
3.945
Svar: 1.9 respektive 3.9 m
Håkan Strömberg
4
KTH STH
Problem 5. I en liggande halv cylinder finns vatten som figuren visar. Givet dessutom vinkeln
∠BAD = 35◦ . Beräkna höjden h
Lösning: Vi startar med att dra radien BE vinkelrätt mot vattenytan. I △BDA har vi hypotenusan
given till 30 cm och ∠BAD = 35◦ . Vi kan då bestämma sträckan BD som vi betecknar med x och
får
x
sin 35◦ =
30
x = 30 · sin 35◦
x
≈ 17.2
Den efterfrågade sträckan h = 30 − 17.2 = 12.8 cm
Svar: 12.8 cm
Problem 6. Beräkna exakt triangelns a) area och b) omkrets
Lösning: För att kunna exakt bestämma area och omkrets till △ABC måste man känna till följande:
• △ACD är en halv kvadrat. Vinklarna är 45◦ , 45◦ , 90◦ . Detta för√med sig att sträckorna CD =
AD = 1. Sträckan AC kan bestämmas med Pythagoras sats till 2. Dessutom är det så att
1
sin 45◦ = cos 45◦ = √
2
• △CBD är en halv liksidig triangel. Vinklarna är 30◦ , 60◦ , 90◦ . Detta för med sig att sträckan
CB = 2 är dubbelt så lång som sträckan CD = 1. Dessutom är det så att
sin 30◦ = cos 60◦ =
1
2
• Genom Pythagoras sats kan man nu bestämma sträckan BD
22 = 12 + BD2
som ger BD =
√
3
Alla önskade sidor är kända och vi kan bestämma omkretsen till
√
√
√
√
O=1+ 2+2+ 3=3+ 2+ 3
Arean blir
A=
Håkan Strömberg
1 · (1 +
2
5
√
3)
KTH STH
Svar: Omkretsen är 3 +
√
√
√
2 + 3 l.e. och arean (1 + 3)/2 a.e.
Problem 7.
Beräkna exakt längden av AD
Lösning: △ABC är en halv
√ liksidig triangel. Efter samma resonemang som i föregående uppgift får
vi då: BC = 1 och AB = 3. △CBD är också en halv liksidig triangel. Det betyder att ∠CDB = 60◦ .
Anta att sträckan DC är x. Vi får då ekvationen
Detta betyder att sträckan AD =
Svar: Sträckan AD =
√
3−
tan 60◦
=
x
=
x
=
√1
3
=
1
x
1
tan 60◦
1
√
3
√2 .
3
√2
3
Alla trianglar här är rätvinkliga
Läxa 1.
Bestäm x.
Läxa 2.
Bestäm x.
Håkan Strömberg
6
KTH STH
Läxa 3.
Bestäm x.
Läxa 4.
Bestäm x.
Läxa 5.
Bestäm v.
Läxa 6.
Bestäm v.
Läxa 7.
Bestäm v.
Håkan Strömberg
7
KTH STH
Läxa 8.
Bestäm v.
Läxa Lösning 1. Rätvinklig triangel med vinkel och närliggande katet given. Motstående katet
efterfrågas.
motstående
tan v =
närliggande
ger
x
tan 34◦ =
35
x = 35 tan 34◦
x
≈ 23.6
Svar: 23.6 cm
Läxa Lösning 2. Vinkel och hypotenusan given. Närliggande katet efterfrågas.
cos v =
närliggande
hypotenusan
ger
x
61
61 cos 40◦
cos 40◦
=
x
=
x
≈ 46.7
Läxa Lösning 3. Vinkel och motstående katet givna. Närliggande katet efterfrågas.
tan v =
motstående
närliggande
tan 56◦
=
x
=
x
≈
43
x
43
tan 56◦
29
Svar: 29 cm
Läxa Lösning 4. Vinkel och hypotenusa givna. Motstående katet efterfrågas.
sin v =
motstående
hypotenusa
ger
x
75
75 · sin 53◦
sin 53◦
=
x
=
x
≈ 59.9
Svar: 59.9 cm
Håkan Strömberg
8
KTH STH
Läxa Lösning 5. De två kateterna givna. Vinkel efterfrågas.
tan v =
motstående
närliggande
ger
tan v
=
v
=
27
42
27
arctan
42
33◦
v ≈
Svar: 33◦
Läxa Lösning 6. Hypotenusan och närliggande katet givna. Vinkel efterfrågas.
närliggande
hypotenusan
cos v =
ger
sin v
=
v
=
44
56
44
arcsin
56
51.79◦
v ≈
Svar: 52◦
Läxa Lösning 7. Hypotenusan och motstående katet givna. Vinkel efterfrågas.
sin v =
motstående
hypotenusa
ger
sin v
=
v
=
50
73
50
arcsin
73
43◦
v ≈
Svar: 43◦
Läxa Lösning 8. Närliggande och motstående katet givna. Vinkel efterfrågas.
tan v =
motstående
närliggande
ger
tan v
=
v
=
23
30
23
arctan
30
37.48◦
v ≈
Svar: 37◦
Håkan Strömberg
9
KTH STH