Matematik A

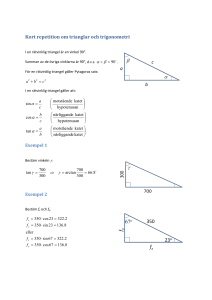
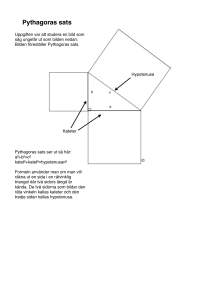
Introduktion i trigonometri
Vad betyder trigonometri?
Man kan dela upp ordet i tre delar:
Tri, som betyder tre
Gon, som har med vinkel att göra (vinkel heter gonia på grekiska)
Metri, som betyder mätning
Vad har du för nytta av trigonometri?
Med hjälp av trigonometri kan du beräkna okända sidor eller vinklar i trianglar. I fysiken
har du användning av trigonometri i t ex optik (ljusets brytning) och mekanik (krafter)
Exempel 1
Tänk dig en backe där stigningen är 3 meter på 20 meter. Se figuren.
20
v
3
Denna stigning hör ihop med en viss lutning. Vi kan uttrycka lutningen på olika sätt:
3
15

 0,15  15%
Lutningen är
20 100
Talet 0,15 hör ihop med precis den här lutningen.
Talet 0,15 hör då ihop med en bestämd vinkel. När vi beräknade
mellan två sidor, närmare bestämt
3
var det en division
20
motstående katet till v
.
hypotenusan
Denna kvot kallas för ”sinus v” som förkortas sin v.
Alltså gäller för denna vinkel sin v = 0,15.
Hur stor är då vinkeln i grader?
Ja det kan man ta reda på genom att använda en räknare som har denna funktion.
Tryck på knappen INV, SHIFT eller 2nd och sedan på SIN 0,15 Resultatet blir avrundat
8,6 grader. (Räknaren måste vara inställd på vinkelmåttet DEG, degrees, som betyder
grader, där 360 grader är ett helt varv.)
Exempel 2
Antag att vi i stället ska beräkna en okänd sträcka i en triangel.
Se figur. Hur stor blir sidan x?
x
52
50
Genom att beräkna sin 52 får vi veta förhållandet mellan motstående katet och
hypotenusan. Alltså
x
sin 52  
vilket ger att x  50  sin 52   39
50
Vilka olika trigonometriska funktioner finns det?
Jag har hittills bara nämnt sinus. Definitionen var alltså
motstående katet
sin v 
hypotenusan
På liknande sätt definieras andra kvoter mellan sidorna:
närliggand e katet
cosinus v  cos v 
hypotenusan
motstående katet
tangens v  tan v 
närliggand e katet
Variant på exempel 2
I triangeln är en vinkel 52, en vinkel är 90. Hur stor är den tredje?
Du svarar säkert 38, vinkelsumman i en triangel är ju alltid 180.
Om vi vill kan vi använda vinkeln 38 istället för beräkning av sträckan x.
x
cos 38  
Lös ut x så ser du att det blir samma svar.
50
Om vi vill beräkna den andra kateten, kan vi göra t ex så här:
y
cos 52  
50
När två sidor i en rätvinklig triangel är kända, kan den tredje beräknas på ett annat sätt
också. Kommer du ihåg hur?
Mera om trigonometri
I Räkna med Vux Ma A handlar kapitel 8 om trigonometri. På Gleerups hemsida finns ett
diagnostiskt prov.