trigonometri övning
advertisement

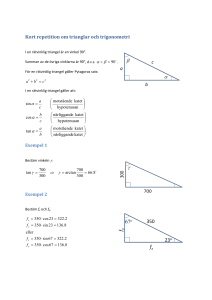
Hur skall man använda trigonometriska funktioner för att finna sidor och vinklar i trianglar? 1. De enklare lösningarna kan bara användas i rätvinkliga trianglar. Så kolla om det finns en rätvinkel eller om man kan dela upp figuren i räta trianglar. 2. Trigonometriska funktioner bildar samband mellan 2 sidor och en vinkel. Vad söker du? a) en vinkel- då måste du känna till 2 sidor (eller de andra vinklar och använda vinkelsumma i en triangel) b) en sida - då måste du kunna en sida och en (spetsig) vinkel (kan du de två andra sidorna- kan du använda Pytagoras sats i stället) 3. Hur förhåller sidorna sig till (den sökta eller kända) vinkeln? Närliggande (=den av de vinkelräta sidorna som bildar ett ben av vinkeln), Motstående och Hypotenusan (= alltid längsta sidan och motstående till räta vinkeln). OBS det är inte om sidan är vågrätt eller lodrätt som är viktigt, ej heller vilka bokstäver som betecknar de använda sidorna, utan hur de ligger i förhållande till vinkeln man vill knyta sidorna till. Namn 4. Vilka sidor som kan kopplas till den sökta eller kända vinkeln bestämmer vilket trigonometriskt samband till höger som du skall använda. sinus Allmän beskrivning sin v = Formelsamlingens kortbeskrivning sin A = motstående hypotenusan a c cosinus cos v = närliggande hypotenusan cos A = b c tanv = motstående närliggande tan A = a b tangens 5. Lös ut det som söks med vanliga ekvationsregler Exempel: v = 37º Höjden= h v h = 6,2m Sök s ! Lösning: i exemplet, till vinkeln v är h = närliggande sida och s = hypotenusan då får vi använda cosinus funktionen: 6 ,2 m cos v = hs ⇔ s = cosh v = cos 37 ° ≈ 7 ,8m s =staglängd I övningarna på nästa sida skall du träna dig på att bilda en ekvation som säger hur du skall räkna ut x (= en sida) eller X (= en vinkel). Versaler (stora bokstäver) betecknar vinklar och gemena (=små bokstäver) betecknar sidolängder. Du skriver lämpligen som den kursiverade texten i lösningsexemplen nedan. Första steget blir att välja en standardformel som du kan använda. De flesta blir baserade på de trigonometriska sambanden ovan men även Pytagoras sats a2 + b2 = c2 eller vinkelsumman i en triangel 180º = A + B + C kan finnas med för att hålla dig uppmärksam. I. II. III. IV. M x x D k m k Lösning: till D är x den Lösning: till M är k den motstående och m närliggande motstående sidan och x hypotenusan så: sidan så: tan D = x/m få x ensam genom multiplikation sin M = k / x med m: x = m · (tan D) man skriver oftast hel enkelt: få x ur nämnaren genom multiplikation med x: x = m tan D få x ensam genom division med sin M: x · sin M = k d x m X Lösning: Vi har 3 sidor Lösning: till X är w den som skall kopplas ihop i en närliggande sidan och m rätvinklig triangel: Pytagoras hypotenusan så: sats Cos X = w/m d2 + x 2 = k 2 x 2 = k 2 - d2 x= Man kan skriva: X = arccos (w/m) Och man räknar på kalkylator så här: k2 - d 2 [cos -1] (w/m) [Exe] x = k / (sin M) SSVH w Jeff Forssell fil: M:\MaAllm\trigGrnd5W97.doc version 01-11-29 Äldre rälknare: (w/m) [cos-1][=] 10:22 sida 1 Övning: Ställ upp en lösning (liknande den kursiverade texten i exemplen på förklaringsbladet) för sida x eller vinkel X i dessa rätvinkliga trianglar. Facit finns nedan 1. 2. x 3. a x A 5. A 6. c b x A 8. a b A 9. x X c b X 11. c b 12. B a x a 10. c c A 7. x A 4. B x B x a X b 13. 14. X x 15. R B 16. B x c a c d x x 17. m A 18. 19. F 20. D x x c a x c s b b 21. X 22. 23. A V b 24. V x X x a k X b Facit c · (sin A) skriver man : 1) x = a/sin A 5) x= b tan A 2) x = b/ cosA 6) x = a/tan A 9) sin X = a/c 13) cos X = a/c 17) x = b/tan D 10) x = c cos B 14) x = c sin B 18) tan X = c/b c sin A oftast 3) x = c sin A 7) tan X = a/b eller X = arctan (a/b) 11) x = b/sin B 15) x = d sin R 19) x = a/cos F 4) x = c cos A 8) cos X = b/c eller X = arccos(b/c) 12) x = a tan B 16) x = m/tan A 20)* x = s 24) x = k/sin V 2 21)* X = 90° - V 22)* X = ½90° = 45° 23) x = a/tan A * 20 -22 är slamkrypare som inte bygger på trigonometriska funktionerna SSVH Jeff Forssell fil: M:\MaAllm\trigGrnd5W97.doc version 01-11-29 10:22 sida 2 − c2