PowerPoint-presentation
advertisement

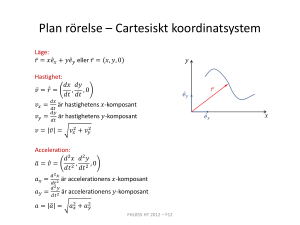
Dugga 30 nov • • • • • Kraft och acceleration (repetition idag) Dimensionsanalys Någon koppling vardagsobservationer -fysik Linjärisering Mätosäkerheter – felfortplantning Idag: kortpauser för er att diskutera och lösa några uppgifter Solur Ingenjörskonst + vetenskap Tidiga rötter: Statik eller Dynamik? • • • • Erfarenhetsbaserad Teknik ? Astrologi ? Geometri ? Naturfilosofi ? Newtons 1a En kropp förblir i ett tillstånd av Vila eller Likformig, Rätlinjig Rörelse om den inte påverkas av en kraft … Tröghetslagen Newton Galileo Likformig rätlinjig rörelse Vila Bil på väg uppför backe. Vilka krafter verkar på bilen? Rita alla krafter i samma skala! Vad ska man tänka på? • • • • Konstant hastighet - Newtons 1:a Summan av alla krafter = 0 Tyngdkraft + Friktionskraft + Normalkraft = 0 Vilken kraftpil är längst? Vad är svårt /lurigt? Newtons etta - exempel Krafter på en bil som kör framåt med konstant hastighet På plan mark ? Nedför en backe ? Uppför en backe ? Rita kraftdiagram. Blir kraftsumman = 0 ? Vad händer med krafterna ... När bilen startar? Stannar? Ur Principia Hur många olika sätt att flyga Vilka olika principer finns för att "hålla sig kvar" över jorden ? Försök att hitta på några olika principer som används ! Allmänna gaslagen Newton och äpplet • "Månen faller till jorden" "Månen är ett äpple" "Månen är en jord" - lyder samma lagar (jfr Aristoteles – cirkulära / linjära rörelser) Det behövs ett geni som Newton för att se att månen faller när alla kan se att den inte gör det (Paul Valery) På Jättars Skuldror • ”If I have seen further [than certain other men] it is by standing upon the shoulders of giants.” Isaac Newton (1642 – 1727) Galileo Galilei 1564-1642 Den moderna naturvetenskapens fader Pendelur, kikare, experiment, idealiseringar Tröghetslagen, Dimensionsanalys … Acceleration? Hastighetsökning? Ändring av hastighet … per tidsenhet (a-g)/g När är hastigheten störst? Noll? Mest negativ? När är man längst ner? Högst upp? N2: F = ma Vad är acceleration? • I Vardagen? • I Fysikboken? • Hur kan man mäta acceleration ? Skriv ned några olika exempel på rörelse med acceleration ≈ 1g. (T.ex. på Liseberg) Acceleration - horisontellt • För att ändra 10 grader – från 0 till 50km/tim på hastighet (fart eller 8s riktning) krävs en KRAFT. • Med ett lod (t.ex. gosedjur i snöre) och en gradskiva kan vi mäta acceleration. Gosedjuret hänger snett på grund av accelerationen! I cirkelrörelse ändras inte farten – bara riktningen Att mäta acceleration – och g-kraft gkraft g a g är tyngdaccelerationen – nedåt a är centripetalaccelerationen – inåt ”g-kraft” blir den kraft (per kg) som verkar på gosedjuret Acceleration ? ”Mellan gravitation och tyngdlöshet” (Monica Sand) Vilken skillnadz är det mellan krafterna i en ”vanlig” gunga och Slänggungan? Kraft och acceleration längst ned? I vändlägena? R=20m Största vinkel: 60 grader r=4.5m Rotation: 9.5 varv/minut Pendel - mätosäkerhet Var under svängningen mäter man perioden bäst ? Hur noga kan man bestämma “g” ? g = k L / T^2 Kombination av mätosäkerheter DL och DT ger Dg = ? Dg / g = ? KRAFTER I RAINBOW? Skillnad mot loop? Dimensionsanalys Storleksordningar Granens kedjor Såpbubblors tryck Muffinsformar Skruvade bollar Gulliver Gaslagen: pV=nRT Ballongers lyftkraft Kanonens utskjutning Vad håller bilen uppe Bernoulli - härled! •VILKET ARBETE UTFÖR TRYCKET PÅ YTORNA? •HUR HAR POTENTIELLA OCH KINETISKA ENERGIN ÄNDRAT? Bernoullis lag Barometer-formel Betrakta luftpelare med yta A och ett luftpaket med höjd dh. p(h+dh) = p(h) – g dh dp/dh = - g = -Mmol*(p/RT) g p(h) /p0 =exp( -Mmol gh/RT) Kastparabeln – numerisk lösning Rörelseekvation: Matlab kod: function test() % Exempel: v0 = 30 m/s, vinkel 36 grader v0=30; u=36*pi/180; x0=0; y0=0; vx0=v0*cos(u); vy0=v0*sin(u); tfinal=2*vy0/9.81; [t,Y]=ode45(@nodrag,[0 tfinal],[x0 vx0 y0 vy0]); x=Y(:,1); y=Y(:,3); plot(x,y); Skriv om rörelseekvationen som ett system av första ordningens differentialekvationer function dYdt = nodrag(t,Y) % ODEFUN(T,Y) ska returnera en kolonnvektor g=9.81; dYdt=zeros(4,1); dYdt(1)=Y(2); dYdt(2)=0; dYdt(3)=Y(4); dYdt(4)=-g; eller höjd (m) längd (m) Fysiken omkring oss, sid 4/16 Göran Wahnström, Institutionen för Teknisk fysik, Chalmers Luftmotstånd i 2 dimensioner ? • • • • v =(3, 4) m/s Luftmotstånd - motriktat rörelsen FD = k v2 Skriv ned accelerationen i komponentform! Hävstång Koordinatsystem Medföljande koordinater ”Pitch – yaw – roll” = Tippa – gira – rolla , a (vid 45 s) Hur stor blir radien? s a = r ^2 Hur stor är accelerationen Diagrammet visar "g-kraft". Vilken typ av rörelse? Osäkerhet i t, , r, (vid 45 s) s a = r ^2 ger r =24m för a= -1.2g Osäkerhet? Vad dominerar ? Värdesiffror ? T(s) 1,22 v(m/s) 12,9 1,31 12,0 1,37 11,4 Användbara formler för berg- och dalbanor Energiprincipen: v2 = 2 g Dh Centripetalacceleration: ac=v2/r =r 2 (ev både horisontellt och vertikalt) Kombinera: ac = 2 g Dh/r ”g-kraft”: Vektoraddition: (a-g)/g Sista snurren Spårets lutning: 53o Krökningsradier: •Vertikalplan r= 30m •Horisontalplan R=13m Höjd: h=24 m Starthöjd: H=65m Höjdskillnad: Dh=41m Teoretisk maxfart: v=29m/s=103km/h av = 2gh/r = 2.7g ah = 2gh/R= 6.3g ”g-kraft”= ? Frikroppsdiagram i olika situationer • Vila • Likformig rätlinjig rörelse • Känd acceleration • Kraftens riktning känd • • • • 1 dimension Rörelse i plan Pendlar Cirkelrörelser (vert/horis) • 3 dimensioner