anteckningar om sparande, inv och bytesbalans

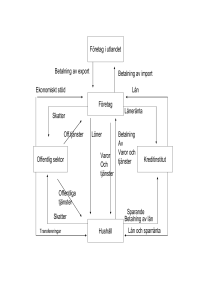
SPARANDE; INHEMSKA INVESTERINGAR OCH BYTESBALANSEN.
Läs: Berg, kap. 17.
Repetion från makrokursen:
NATIONALRÄKENSKAPER II: Nationellt
investeringar, handelsbalansen och bytesbalansen.
finansiellt
sparande,
inhemska
Antag en sluten ekonomi: Dvs en ekonomi utan utrikeshandel: BNI = BNP = C + I + G
“inkomstmått” = “produktionsmått” = C + G + I
 Nationellt finansiellt sparande, S = BNI – C – G = I
 Nationellt finansiellt sparande (= inkomst – (privat konsumtion + offentlig konsumtion och
investeringar)) = privata bruttoinvesteringar
I statistiken från Statistiska Centralbyrån och Finansdepartementet men inte i läroböcker
brukar G delas upp i GC och GI; dvs. G = GC + GI.
Där GC = offentlig konsumtion och GI = offentliga investeringar.
BNI = C + I + GC + GI
 S = BNI – C – GC = I + GI
 Nationellt finansiellt sparande (= inkomst – konsumtion (privat och offentlig)) = privat och
offentliga bruttoinvesteringar. Dvs denna definition på nationellt finansiellt sparande brukar
användas av myndigheter.
Jag använder läroboksbeteckningen; G framledes:
Dvs. vi delar i allmänhet inte upp G i GC och GI.
Uppdelning av nationellt finansiellt sparande I privat och offentligt finansiellt sparande:
Modellantagande: T = skatter, netto (= offentliga skatteintäkter – offentliga utgifter för
transfereingar). Trots att det I verkligenheten finns många olika skatter så klumpar vi ihop
dem här. Om T > 0, då är de offentliga skatteintäkterna > offentliga transferingsutgifterna.
I verkligheten så brukar T>0 eftersom skatteintäkter inte bara skall täcka utgifter för
transferingar utan även betala för offentlig konsumtion och offentlig investeringar.
 BNI – T = hushållens disponibla inkomst
Dvs under antagande att kapitalförslitningen är 0.
I verkligheten är nettoskatter, T, positivt relaterade till inkomsten, BNP. Dvs. T är procyklisk,
T ökar när BNP ökar eftersom skatteintäkter ökar och transferingsutgifter minskar i
högkonjunktur (när faktisk Y ökar relativt potentiell real BNP). Potentiell BNP är nivån på
BNP som uppstår när den faktiska arbetslösheten är lika med den naturliga arbetslöshetsnivån.
I en lågkonjunkur, när Y faller nedanför den potentiella nivån, så faller skatteintäkterna
medan transferingsutgifterna ökar eftersom det blir ökade utgifter för arbetslösa.
Ofta, i ekonomiska modeller, antas att skatteintäkterna = t*BNP, där t är skattesatsen, t ex. 0.4
(dvs, 40 procent). Denna formulering innbär att skatteintäkterna ökar när BNP ökar. I en
lågkonjunktur tenderar skatteintäkter att fallar medan transferingsutgifter (t ex utgifter för
arbetslösa) ökar. I en högkonjunktur råder det motsatta förhållandet.
Föreläsning:
Det faktum att skatterna, netto, tenderar att öka i högkonjunktur och minska i lågkonjunktur
brukar kallas en så kallad AUTOMATISK STABILISATOR. Dvs en stabilisator som tenderar
att jämna ut hög och lågkonjunktur. Lägre skatter, netto, I en lågkonjunkur innebär att
hushållens disponibla inkomster faller mindre än vad de skulle ha gjort om regeringen varit
tvungen att ha en balanserad budget. Dvs. Att intäkter är lika med kostnaderna. Om disponibla
inkomsten faller mindre så innebär det att den privata konsumtionen och därmed den
aggregerade efterfrågan faller mindre än den skulle ha gjort om den offentliga sektorn
balanserade sin budget.
S = BNI – C – G = I
 Nationellt finansiellt sparande (S) = I
 S = BNI – C – G + T – T = I
 S = (BNI – T – C) + (T – G) = I
 Nationellt finansiellt sparande (S) = privat finansiellt sparande + offentligt finansiellt
sparande = I
Offentliga sektorns finansiella sparande =offentliga sektorns budgetöverskott =
Offentliga skatteintäkter – offentliga utgifter (offentlig konsumtion+ offentliga investeringar
+transferingsutgifter).
Den öppna ekonomin: Handelsbalansen och bytesbalansen
BNP (Y) = C + I + G + NX (=Export – Import av nyproducerade varor och tjänster)
 NX = BNP – (C+I+G) = Inhemsk produktion – ”inhemsk absorbtion”
 Om den inhemska produktionen av varor och tjänster överstiger ”den inhemska
absorbtionen av varor och tjänster”, då är exporten större än importen.
Med andra ord, handelsbalansen, NX, är positiv.
Nationellt finansiellt sparande:
 BNI = BNP + faktorinkomster från utlandet, netto (NFI) = C + I + G + NX + NFI
 Nationellt finansiellt sparande, S = BNI – C – G = I + NX + NFI
där NX + NFI = bytesbalansen
 Nationellt finansiellt sparande = inhemska privata investeringar + bytesbalansen.
Bytesbalansen kallas ibland investeringar I utlandet, netto. Nationellt sparande är antingen
investerat i hemlandet eller i utlandet. Antag att NFI = Net Foreign Income =0, och att NX>0.
Det innebär att exportvärdet är större än importvärdet vilket innebär att utlandet kommer I
skuld till Sverige. Detta är en finansiell investering.
Föreläsning:
Om man skall vara exakt, så skall man även räkna in tranfereringar från utlandet, netto, I
bytesbalansen och i det nationella sparandet. För transfereringar från utlandet använder jag
nedan förkortningen NFTr = Net Foreign Transfers. NFTr har ökat på senare år då världen
globaliserats. Många utländska medborgare skickar pengar till släkt i hemlandet.
 BNI + transfereringar från utlandet, netto (NFTr) = C + I + G + NX + NFI + NFTr
 Nationellt sparande, S = BNI + NFTr – C – G = I + NX + NFI + NFTr
där NX + NFI + NFTr = bytesbalansen (investeringar I utlandet, netto)
 nationellt sparande (S) = privata inhemska bruttoinvesteringar + bytesbalansen
Om NFI och NFTr är relativt stabila över tiden, så innebär det att förändringar I nationellt
sparande och förändringar i privata inhemska bruttoinvesteringar avspeglas i bytesbalansen.
Om det nationella sparande överstiger de privata inhemska investeringarna, så är
bytesbalansen positiv.
I statistiken från t ex Finansdepartementet brukar G delas upp I GC och GI:
 S = BNI + NFTr – C – GC = I + GI + NX + NFI + NFTr
 nationellt finansiellt sparande (S) = privata och offentliga inhemska bruttoinvesteringar +
bytesbalansen (investeringar I utlandet, netto)
Om vi går tillbaka till formuleringen där G = GC + GI när vi delar upp det nationella
finansiella sparandet i privat och offentligt:
 S = BNI + NFTr – C – G + T – T = I + NX + NFI + NFTr
 (BNI + NFTr – T – C) + (T – G) = I + NX + NFI + NFTr
 (privat finansiellt sparande) + (offentligt finansiellt sparande) = privata inhemska
bruttoinvesteringar + bytesbalansen (investeringar I utlandet, netto)
Tillämpning: “Tvilling underskott”.
Ett offentligt budgetunderskott, G-T>0, genererar ett bytesbalansunderskott om den inhemska
privata investeringarna (I) är konstant och även det privata finansiella sparandet.
T ex om militärutgifterna för irakkriget: G (T-G)  NX 
Slutsats:
Nationellt finansiellt sparande = GDP (Y) + faktorinkomster från utlandet, netto (NFI) +
transfereringar från utlandet, netto (NFTr)
 nationellt finansiellt sparande (S) = BNI + NFTr– (C+G) = I + NX + NFI + NFTr
där NX + NFI + NTr = bytesbalansen
Modeller (se nedan) förenklar i allmänhet verkligheten:
I Keynes modell och den klassiska modellen antas i allmänhet att NFI=NFTr = 0:
S= Y-(C+G)=I +NX.
Vidare antas oftas (till skillnad från i Solow-modellen) att förslitningen av det fysiska
kapitalet är 0:
 Skatter (direkta+indirekta+sociala avgifter+ etc) + arbetsinkomster efter skatt +
kapitalinkomster efter skatt = BNP (Y) = C + I + G+ NX
Dvs. skatter+arbetsinkomster efter skatt +kapitalinkomster efter skatt = BNI(Y)=BNP(Y).
TEORI: Den Keynesianska modellen för en sluten ekonomi på lång sikt =
Den klassiska modellen för en sluten ekonomi.
Grundantagande: fullt resursutnyttjande. Läs Berg, kap. 17 och ev också OSP 7.6.
I den klassiska modellen leder inte förändringar i det nominella penningutbudet till att reala
variabler förändras som t ex real BNP. Därför bortser vi ifrån penningmängden i modellen.
Orsaken till att penningpolitik inte påverkar real BNP beror på att löner och priser antas vara
helt flexibla. Inte heller finanspolitik påverkar real BNP som alltid är lika med potentiell
BNP. Däremot kan finanspolitik påverka andra reala variabler som realräntan och de reala
privata investeringarna.
I den Keynesianska modellen är löner och priser flexibla på lång sikt men inte på kort sikt.
Jag brukar tänka på lång sikt att det gäller i genomsnitt för en ekon
Flexibla löner och priser innebär att produktionsfaktorerna är fullt utnyttjade. Dvs. Efterfrågan
på K och L är lika med utbudet av K och L som antas vara fixt vid en given tidpunkt.
Om utbudet av arbete och kapital är fixt, så är även utbudet av varor och tjänster fixt:
Y  F ( K , L)  Y
Ett streck ovanför K och L innebär ett fixt utbud. Det fixa utbudet av K och L efterfrågas pga.
antagandet om flexibla priser.
Hur uppnås jämvikt på varumarknaden vid fullt resursutnyttjande som i genomsnitt
gäller för en ekonomi? Jämvikt på varumarknaden innebär:
Aggregrat utbud (Y) = aggregerad efterfrågan på nyproducerade varor och tjänster (AD)
Y  AD  C  I  G  C(Y  T )  I (r)  G
där Y=GDP=GNP .
Jämvikt på varumarknaden på lång sikt; dvs när
Y  F (K , L) :
Y  AD  C (Y  T )  I (r)  G
Notera: realräntan, r, är den enda variabel som inte redan är förutbestämd.
M.a.o., spelar r en nyckelroll: den anpassas så att efterfrågan blir lika med utbudet.
En hög realränta innebär en låg nivå på reala investeringar, och därmed en låg aggregerad
efterfrågan på nyproducerade varor och tjänster.
Realränta ser till att den finansiella marknaden hamnar I jämvikt, som även innebär jämvikt
på varumarknaden:
Ett minskat offentligt sparande minskar det nationella sparande och ökar realräntan:
Real
interest
rate, r
S'
Saving, S
AAreduction
reductionin
insaving,
saving,possibly
possiblythe
the
result
of
a
change
in
fiscal
policy,
result of a change in fiscal policy,
shifts
shiftsthe
thesaving
savingschedule
scheduleto
tothe
theleft.
left.
The
Thenew
newequilibrium
equilibriumisisthe
thepoint
pointatat
which
whichthe
thenew
newsaving
savingschedule
schedulecrosses
crosses
the
investment
schedule.
A
reduction
the investment schedule. A reduction
in
insaving
savinglowers
lowersthe
theamount
amountof
of
investment
investmentand
andraises
raisesthe
theinterest
interestrate.
rate.
Desired Investment, I(r)
Investment, Saving, I, S
S
Fiscal
Fiscalpolicy
policyactions
actionsare
aresaid
saidto
tocrowd
crowdout
outinvestment.
investment.
I Om G
 Nationellt finansiellt sparande: S  (Y  C(Y  T )  G )  ,
Om vi delar upp nationellt finansiellt sparande i privat finansiellt sparande (hushållens
finansiella sparande) och offentligt finansiellt sparande:
S  (Y  T  C(Y  T ))  (T  G ) 
Y  T  C(Y  T ) , är konstant.
Det offentliga finansiella sparandet, (T  G)  , minskar.
Hushållens finansiella sparande,
II Om T
(Y  T )   C(Y  T )  , S  (Y  C(Y  T )  G)  ,
S  (Y  T  C(Y  T ) )  (T  G)  



Privat finansiellt sparande Y  T  C(Y
ökar när T minskar eftersom MPC <1.
Offentligt finansiellt sparande,
T ) 
ökar eftersom Y-T ökar mer än C
T  G , minskar.
Slutsats: Om G  och/eller T  (som ökar C)  I(r)
Y  C (Y  T )  I (r)  G
En ökning av G, minskar offentligt och nationellt sparande och minskar de privata
bruttoinvesteringarna via en ökad realränta.
Lägre skatter, netto, (T) ökar disponibel inkomst (Y-T), som ökar C, och minskar nationellt
sparande, Y-C-G, som sänker investeringarna via en ökad realränta.
Med andra ord: Ett minskat offentligt sparande via en ökad offentlig efterfrågan på varor och
tjänster (G) eller lägre skatter, netto (T) minskar det nationella sparande och därmed de
privata bruttoinvesteringarna i fasta priser genom en högre realränta.
Total efterfrågan är oförändrad. Den är lika med det totala utbudet ( Y ) som är oförändrat.
Vår slutsats att en expansiv finanspolitik (ökad G och/eller minskad T) minskar det offentliga
och nationella sparandet och därmed driver upp realräntan påverkas inte ifall vi låter det
privata sparandet, Y –T –C, öka med högre realränta.
Dvs. om vi låter den privata konsumtionen minska med högre realränta: C(Y-T, realränta).
Det nationella sparandet blir nu: Y-T-C(Y-T, realräntan):
S(r)
Real
interest
rate, r
B
I2
A
I1
Investment, Saving, I, S
When saving is positively related to the interest rate, as shown by
the upward-sloping S(r) curve, a rightward shift in the investment
schedule I(r), increases the interest rate and the amount of
investment. The higher interest rate induces people to increase
saving, which in turn allows investment to increase.
Om hushållens sparande ökar när realräntan ökar, innebär det att hushållens konsumtion
minskar när realräntan ökar, eftersom sparande och konsumtion är lika med hushållens
disponibla inkomst, Y  T , som i den klassiska modellen är bestämd utifrån tillgången på
produktionsfaktorer.
Om nationellt sparande är orelaterat till realräntan så innebär ett skift i investeringsfunktionen
utåt endast att realräntan ökar.
Ett högre intercept, I  , skiftar investeringskurvan utåt,
om företagens förväntningar om framtiden ökar.
I  I  d  r , vilket skulle inträffa
Den Keynesianska modellen för en liten öppen ekonomi på lång sikt =
Den klassiska modellen för en liten öppen ekonomi.
För en liten öppen ekonomi. För en liten öppen ekonomi är realräntan lika med
världsmarknadsräntan, r * , i jämvikt.
Flexibla löner och priser innebär att faktisk BNP är lika med BNP vid full sysselsättning
Förenklande antagande: Antag att nettoinkomster från utlandet, netto (NFI) och transferingar
från utlandet, netto (NFTr) är lika med 0.
 BNP (Y) = BNI, handelsbalansen = bytesbalansen
Jämvikt på varumarknaden:
Y  C(Y  T )  I (r  r*)  G  NX (real växelkurs  e($/ kr)  P(kr)  / P($)
 Nationellt sparande (S) =
Y  C (Y  T )  G  I (r  r*)  NX ( )
S  I  (Y  C(Y  T )  G)  I (r* )  NX (e  P / P* )
Antag att den offentliga sektorn minskar sitt finansiella sparande via en ökad G och/eller via
en sänkt T. Det minskar det nationella sparande vilket leder till en minskad NX. De inhemska
bruttoinvesteringarna är oförändrade eftersom realräntan är given och lika med
världsmarknadsräntan. Den reala växelkursen apprecieras eftersom på något annat sätt kan
inte NX minska i denna modell. Dvs. en expansiv finanspolitik tränger ut nettoexporten
Y  C (Y  T )  I (r*)  G  NX (real växelkurs)
Real
exchange
rate, 
2
1
S2-I
S1-I Expansionary fiscal policy at home, such as an
increase in government purchases G or a cut in
taxes, reduces national saving.
The fall in saving reduces the supply of dollars
to be exchanged into foreign currency, from
S1-I to S2-I. This shift raises the equilibrium real
exchange rate from 1 to 2.
NX() A reduction in saving reduces
NX2 NX1 Net Exports, NXthe supply of dollars which
causes the real exchange rate
to rise and causes net exports
to fall.
Om G  och/eller T   real växelkurs, NX(real växelkurs,  ),
UPPGIFTER och Svar: Sparande, investeringar och bytesbalans.
Den Keynesianska modellen på lång sikt för en sluten ekonomi = den klassiska modellen.
På lång sikt, när priser och löner är flexibla, är den Keynesianska modellen identisk med den
klassiska modellen. Flexibla priser och löner innebär att faktisk BNP = potentiell BNP.
Ekonomin är vid full sysselsättning, vilket innebär att den faktiska arbetslösheten är lika med
den naturliga arbetslösheten. Vi börjar med att analysera en sluten ekonomi med fullt
resursutnyttjande. Fullt resursutnyttjande innebär att faktisk BNP = potentiell BNP.
Läsning: OSP: Kap. 7.6, 11.2. Berg, kap. 17.
Uppgift 1.
Antag att en ekonomi beskrivs av följande ekvationer:: Y=C+I+G, Y=5000, G=1000,
T=1000, C=250+0.75(Y-T), I=1000-50r.
I modellen antas de privata investeringarna bero negativt på realräntan.
Den privata konsumtionen antas bero positivt på den disponibla inkomsten.
Ibland antar vi också att den privata konsumtionen beror negativt på realräntan, vilket sålunda
innebär att det privata (och nationella) sparande ökar med ökad realränta.
Jämvikt på varumarknaden innebär att Y = C(Y-T)+I(realräntan) + G
Jämvikten på varumarknaden innebär sålunda: S = Y-C(Y-T)-G=I(realräntan).
Ekvationen har en obekant, realräntan.
M.a.o, vi har jämvikt på varumarknaden när det nationella sparandet (S) är lika med de
privata brutto investeringarna.
A. Beräkna privat, offentligt och nationellt sparande samt de privata bruttoinvesteringarna.
B. Beräkna jämviktsräntan.
C. Antag nu att G ökar till 1250. Beräkna privat, offentligt, och nationellt sparande.
D. Beräkna jämviktsräntan.
E. Antag nu att T minskar till 750 (och att G=1000). Beräkna privat, offentligt, nationellt
sparande samt jämviktsräntan samt de privata bruttoinvesteringarna.
F. Utgå t ex ifrån de ursprungliga värdena, ifall privat konsumtion ökar vid en given
disponibel inkomst (interceptet (250) och/eller MPC ökar), vad händer då med realräntan och
de privata bruttoinvesteringarna samt med det nationella sparandet?
Ge ett kvalitativt svar (dvs. ökar, minskar, oförändrad).
G. Ifall de privata investeringarna ökar vid en given realränta pga. bättre framtidsutsikter, vad
händer då med realräntan och de privata investeringarna samt med det nationella sparandet?
Ökar de privata investeringarna?
Uppgift 2. Om hushållens konsumtion minskar när realräntan ökar, åverkar detta antagande de
kvalitativa effekterna av finanspolitik (= förändringar av G och T) på realräntan?
En liten öppen ekonomi vid fullt resursutnyttjande med flytande växelkurs.
En liten öppen ekonomi har en realränta som är lika med realräntan i omvärlden.
Realräntan i världen bestäms av ekvationen världens sparande = Världens bruttoinvesteringar
(realräntan).
Ibland antar man att sparandet beror positivt på realräntan. Jämviktsvillkoret blir då:
Världens sparande(realräntan) = Världens bruttoinvesteringar(realräntan).
Uppgift 1. Antag att ekonomin beskrivs av följande ekvationer:
Y=C+I+G+NX, Y=5000, G=1000, T=1000, C=250+0.75*(Y-T), I=1000-50*r,
r=(r i omvärlden) = 5
NX=500-500*  .  = real växelkurs.
A. Bestäm nationellt sparande, inhemska bruttoinvesteringar, handelsbalansen och
jämviktsväxelkursen (den reala).
B. Antag nu att G ökar till 1250. Bestäm nationellt sparande, inhemska bruttoinvesteringar,
handelsbalansen och jämviktsväxelkursen (den reala). Förklara!
C. Antag smaken i omvärlden förändras, det blir inne med skandinaviska varor. Dvs.
omvärldens efterfråga på våra produkter ökar vid given real växelkurs. Vad kommer hända
med den reala växelkursen, vad händer med handelsbalansen? Ge ett kvalitativt svar.
D. Antag att skatterna (T) sänks, vad händer med nationellt sparande, inhemska privata
bruttoinvesteringarna, handelsbalansen och den reala växelkursen?
Uppgift 2. Om staten ökar G pga. Krig, vad händer med handelsbalansen och den reala
växelkursen? Beror ditt svar på om det är ett regionalt (litet) eller globalt krig.
Svar: Sluten ekonomi med fullt resursutnyttjande
Uppgift 1.
a+b. S = 750, priv S = 750, offentligt S = 0, r = 5 %
c+d. S = 500, priv S = 750, offentligt S = -250, r = 10 %
e. S = 562.5, priv S = 812.5, offentligt S = -250, r = 8.75 %
Nationellt sparande är lika med de privata bruttoinvesteringarna.
f. realräntan ökar och privata bruttoinvesteringarna minskar.
g. Realräntan ökar med de privata bruttoinvesteringarna är oförändrade.
Uppgift 2. De kvalitativa slutsatserna påverkas ej. Men kvantitativt, så innebär en
konsumtionsfunktion som påverkas negativt av högre ränta att en given ökning av G minskar
investeringarna mindre jämfört med fallet där den privata konsumtionen inte påverkas av
räntan.
Svar: Liten öppen ekonomi med fullt resursutnyttjande
Uppgift 1: a.S=I=750, NX=0, reala växelkursen =1.
b.S=500, I=750, NX=-250, reala växelkursen =1.5 .
c. nationellt sparande, de privata bruttoinvesteringarna och handelsbalansen är oförändrade.
Valutan apprecieras realt.
d. Privata bruttoinvesteringarna är oförändrade, nationellt sparande minskar och
handelsbalansen försämras. Valutan apprecierar, realt sett.
Uppgift 2: En ökning av G minskar nationellt sparande, vilket apprecierar den
reala växelkursen, vilket gör inhemska varor och tjänster dyrare och utländska
varor och tjänster billigare, vilket försämrar handelsbalansen, NX.
Ett världskrig innebär lågt nationellt sparande i många länder vilket innebär en
hög
världsmarknadsränta
(den
reala),
vilket
minskar
de
inhemska
investeringarna. Om minskningen av investeringarna är större än minskningen
av det nationella sparande, förbättras handelsbalansen vilket uppnås genom en
real depreciering.