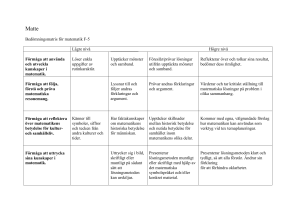
Perspektivet på problemlösning i matematik enligt
advertisement

Lärande och samhälle Natur, miljö, samhälle Examensarbete 15 högskolepoäng på avancerad nivå Perspektivet på problemlösning i matematik enligt den aktuella läroplanen Lgr 11 Perspectives on mathematical problem solving in the current curriculum Lgr11 Saleha Ahmadi Lärarexamen 210 hp Examinator: Peter Bengtsson/ Matematik och lärande Agneta Rehn Datum: 2013-06-05 Handledare: Troels Lange 1 2 Förord Som förord vill jag framhålla ett varmt tack till personerna som bidragit till hjälp och stöd för denna studie. Först och främst vill jag rikta ett varmt och hjärtligt tack till Lena Andersson och Margareta Bynke och övriga matematikpedagoger vid Malmö högskola, lärande och samhälle för en väl bemötande, stöd och uppmuntran under hela min utbildningsgång. Det var era stöd som gjorde att jag fick möjlighet att undersöka ett ämne som alltid har varit intressant. Ett särskilt stort tack till min handledare Troels Lange för hans inspirerande handledning, som aldrig förtröttas att ge mig idéer och vägledning och alltid har hittat nya utgångspunkter, då det uppstått problem. Högskolslektor Eva Reisbeck har haft vänligheten att ge mig värdefulla idéer om uppsatsens titel. Slutligen, tack min underbara familj för ert oerhörda stöd och tålamod genom hela den här processen. Utan er hjälp hade jag inte kunnat genomföra min undersökning. Ett stort tack till er alla! 3 4 Sammanfattning Studiens ursprungliga och övergripande syfte var att ge uppslag till diskussion rörande förändringar och utvecklingar av undervisning i matematik i problemlösning. Wyndhamn, Riesbeck & Schoultz, (2000) redovisade i sin analys hur problemlösning beskrevs i olika officiella dokument så som läroplaner. Wyndhamn et al. valde att beskriva resultaten av sina analyser i termer av tre prepositioner som alla hade använts i samband med problemlösning – för, om och genom. Syftet med min studie var att undersöka dessa förändringar och utvecklingar och ta reda på i vilket perspektiv problemlösning hade framställts i den aktuella läroplanen Lgr 11 jämfört med de tidigare läroplanerna från Lgr 69 (Skolöverstyrelsen, 1969), Lgr, 80 (Skolöverstyrelse, 1980) och Lpo 94 (utbildningsdepartementet, 1994). Studien genomfördes som en textanalys av styrdokument. Resultatet framställde att perspektivet på problemlösning enligt Skolverket (Lgr 11) var byggd på den sociokulturella teorin, där lärarens roll beskrevs som en mediator och organisatör. Lärarens roll förändrades från att överföra, förmedla, handleda information och regler till att organisera och vara resurs för medierade lärandeerfarenheter. Elevens lärande beskrevs som aktivt medierad lärande. Eleven i sin lärande var självgående och självstyrande och sågs som en skapare, en kreatör och framförallt som en frambringare. Alltså kan problemlösning sägas vara framställd i ett nytt perspektiv och förklaras med en ny preposition. Enligt min analys av Lgr 11 skall läraren undervisa i problemlösning i matematik. Studiens slutsatser framhävde att det traditionella för perspektivet i problemlösning skulle förändras, om perspektivet skulle byggas vidare och genom perspektivet skulle granskas och utvecklas inför nästa kommande läroplan. Nyckelord: Elevens lärande, Karaktären hos skolmatematikens uppgifter, Lärarens roll, Läroplan 5 6 Innehåll 1. Inledning ................................................................................................................... 9 1.1 Bakgrund ................................................................................................................ 9 1.2 Studiens syfte........................................................................................................ 11 1.3 Frågeställning ....................................................................................................... 11 2. Teoretisk inramning................................................................................................ 12 2.1 Några teoretiska perspektiv på lärande ................................................................. 12 2.2 Behaviorism .......................................................................................................... 12 2.3 Svag-konstruktivism (kognitivism) ...................................................................... 14 2.4 Social konstruktivism ........................................................................................... 15 2.5 Teoretiskt perspektiv på lärande enligt Lgr 11 ..................................................... 16 2.5.1 Sociokulturellt perspektiv .............................................................................. 16 2.5.2 Kommunikation ............................................................................................. 17 2. 5. 3 Medierande artefakter .................................................................................. 18 2.5.4 Lärarens roll i klassrumskommunikation ...................................................... 18 2.5.5 Teorin om medierade lärandeerfarenheter (MLE)......................................... 19 2.6 En sammanfattande översiktlig jämförelse av lärande- teorier ............................ 19 2.7 Karaktären hos skolmatematikens uppgifter ........................................................ 20 2.7.1 En historisk genomgång av begreppet problemlösning................................. 20 2.7.2. Karaktären hos skolmatematikens uppgift i för perspektivet ....................... 21 2.7.3 Karaktären hos skolmatematikens uppgifter i om perspektivet..................... 22 2.7.4 Karaktären hos skolmatematikens uppgifter i genom perspektivet ............... 22 2.8 Sammanfattning .................................................................................................... 24 3. Val och motivering av metod ..................................................................................... 26 3.1 Datainsamling ....................................................................................................... 27 3.2 Beskrivning av undersökningsförfarande ............................................................. 27 3.3 Etiska överväganden ............................................................................................. 28 3.3.1 Studiens tillförlitlighet ................................................................................... 29 4. Analys och teoretisk tolkning (utifrån Lgr11) ............................................................ 30 4.1 Struktur i den nu rådande läroplanen .................................................................... 30 4.1.2 Förmågor ....................................................................................................... 31 4.1.3 Problemlösningsförmåga ............................................................................... 31 7 4.2 Lärarens roll enligt Lgr 11 .................................................................................... 34 4.2.1 Kommunikationsförmåga .............................................................................. 35 4.3 Karaktären hos skolmatematikens uppgifter enligt Lgr 11 .................................. 36 5. Diskussion .................................................................................................................. 39 5.1 Koppling till frågeställning och resultat ............................................................... 39 5.2 Slutsats .................................................................................................................. 41 5.3 Förslag till fortsatt forskning ................................................................................ 44 6. Referenser ................................................................................................................... 45 8 1. Inledning I detta kapitel beskriver jag hur intresset för mitt ämnesval växt fram. Därefter beskrivs syfte och frågeställning och argumentation till varför denna forskningsfråga anses vara viktigt i lärarprofessionen. I anslutningen till bakgrunden ges en kort genomgång av det som ligger utanför studiens fokus. 1.1. Bakgrund Att säga att skolan – liksom för övrigt all utbildning i dagsläget – befinner sig i en tydlig förändringsfas är egentligen inte något nytt. För att diskussionen om olika omställningar ska bli meningsfull är det av största betydelse att olika utvecklingstendenser synliggörs, och studera hur de beskrivs och sedan värderas (Wyndhamn, Riesbeck & Schoultz, 2000). Som blivande lärare i matematik för grundskolans tidigare år är jag en av de som är intresserad och vill gärna framhålla dessa omställningar i min studie. Avsikten är att beskriva och synliggöra förändringar och utvecklingar i området problemlösning i matematik och genom det utveckla och reflektera en bättre förståelse av och medvetenhet om matematikundervisning. En förståelseinriktad matematikundervisning blir intressantare för både eleverna och läraren och bidrar i sin tur till att förbereda eleverna för kommande studier och livet utanför skolan vilket är ett av de övergripande syftena med problemlösning enligt samtliga läroplaner (Engström, Engvall & Samuelsson, 2007). Ett vidare syfte med studien är den oron som vuxit fram under min verksamhetsförlagda tid för elevernas bristande förmåga att lösa problem. Problemlösningens roll förändras i våra kursplaner för grundskolan under senare hälften av 1900-talet. Wyndhamn et al. (2000) beskriver dessa förändringar genom att använda sig av prepositionerna för, om och genom. Författaren har placerat in vad grundskolans olika läroplaner huvudsakligen ser som problemlösning. I läroplanen för grundskolan Lgr 69 (Skolöverstyrelsen, 1969) och tidigare läroplaner sågs problemlösning som målet för övrigt lärande. I nästa läroplan för grundskolan, från 1980, Lgr 80, (Skolöverstyrelsen, 1980) blev problemlösning ett eget huvudmoment. Läraren skulle undervisa om problemlösning och målet var att eleverna på egen hand sedan skulle klara av att hitta en lämplig lösningsstrategi till de uppgifterna som ställs i matematikundervisningen. I Läroplan för det obligatoriska skolväsendet Lpo 94 (utbildningsdepartementet, 1994)) ser man på problemlösning mer som ett medel att få eleverna att tänka 9 matematiskt och därigenom utveckla sina kunskaper i ämnet. Lärarna ska undervisa i matematik genom problemlösningen (Wyndhamn et al., 2000). Den nuvarande kursplanen Lgr 11 har formulerat kunskapsområdet problemlösning på följande sätt: Genom undervisning i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, (Skolverket, 2011a, s. 62). Vi ser utifrån citatet att det nuvarande läroplanen lyfter fram arbetet med problemlösning som en väsentlig, kreativ och reflekterande aktivitet. En läroplan och tillhörande kursplan är tidsdokument och återspeglar vissa teorier även om det är svårt att i läroplanerna finna några tydliga konkretiseringar av och motiveringar för dem (Wyndhamnet et al., 2000). Som jag kommer att redovisa i denna studie är Lgr 11 i stort sätt byggd på sociokulturella idéer, med tanke på ett kommunikativt drag. I kommentarer till gällande kursplan i matematik står det att viktiga utgångspunkter för förändringar i kursplanen som Third international Mathematics and Science study (TIMSS) och Programme for International student Assessment (PISA) har rapporterat att undervisningen i matematik i stort sätt präglas av enskild räkning, vilket får till följd att eleverna i undervisningen har begränsade möjligheter att utveckla förmåga att lösa problem. Det innebär också att eleverna sällan har fått möjligheter att använda matematik i vardagen och inom olika ämnesområden. Mot bakgrund av detta är ambitionen med nya kursplanen att betona vikten av att eleverna ges möjlighet att använda matematik i olika sammanhang, utveckla förmåga att lösa problem, använda logiska resonemang samt att kommunicera matematik med hjälp av olika uttrycksformer (Skolverket, 2011b)”. Vidare rapporterar Skolverket att internationella studier visar att Svenska elever behärskar de enkla och rutinartade uppgifterna medan uppgifter som efterfrågar analys och problemlösning framstår som problematiska (Skolverket, 2006). Vi ser att min påstående angående elevernas bristande förmåga i problemlösning kommer också överens med de nationella och internationella utvärderingarna gällande elevernas förmåga att lösa matematiska problem. Utifrån de ovanstående rapporteringarna anser jag att problemlösning är en viktig forskningsfråga i lärarprofessionen. Problemlösning är inte bara yrkesmässigt relevant utan också vetenskapligt. Den vetenskapliga relevansen är att genom att lösa problem kan man utveckla tankar, idéer, självtroende, analysförmåga, kreativitet och tålamod. 10 Man lär sig att planera, upptäcka, samband förfina det logiska tänkandet och skaffa sig beredskap att klara situationer i livet (Ahlström et al., 2009). Historisk har utveckling för våra kursplaner gått från att räkna till att lära genom problemlösning. I mycket grova drags ses den problemlösande eleven som härmare i för perspektivet, som informationsbehandlare i om perspektivet och som tänkare i genom perspektivet (Wyndhamn et al., 2000). Hur ses den problemlösande eleven enligt den nya läroplanen? Hur ses lärarens roll och karaktären hos skolmatematikens uppgifter enligt den aktuella läroplanen Lgr 11? Det är dessa frågor som denna studie lyfter fram och söker kunskap genom. Eftersom området problemlösning är mycket vidsträckt begränsas det till att omfatta problemlösning i ämnet matematik och enbart gällande grundskolans tidigare år. Studien diskuterar bara läroplaner från (1969, 1980, 1994 och 2011). För att underlaget inte blir för stor studeras och sedan analyseras varje perspektiv utifrån följande punkter: Karaktären hos skolmatematikens uppgifter Lärarens roll Elevens lärande Sammantaget kan uppsatsen läsas som en redovisning för förändring och utveckling i perspektiven på problemlösning i matematikundervisning. 1.2. Studiens syfte Syftet med undersökningen är att ta reda på i vilka perspektiv problemlösning beskrevs med avseende på elevens lärande, karaktären hos skolmatematikens uppgifter och lärarens roll i de tidigare läroplanerna (1969, 1980 och 1994), samt att undersöka och beskriva perspektivet på problemlösning med avseende på lärarens roll, elevens lärande och karaktären hos skolmatematikens uppgift enligt den aktuella läroplanen Lgr 11 för matematik i grundskolans tidigare år. 1.3 Frågeställning I vilket perspektiv beskrivs problemlösning med avseende på elevens lärande, karaktären hos skolmatematikens uppgifter och lärarens roll i den aktuella läroplanen Lgr 11 jämfört med läroplanerna i 1969, 1980 och 1994? 11 2. Teoretisk inramning För att få förståelse för vilka teorier som Lgr 11 speglar är det viktigt att titta tillbaka på de tidigare lärandeteorierna och se hur dessa utvecklas genom tiden. Därför utförs i detta kapitel en ideologianalys med syfte att belysa vilken syn på lärande läroplanerna uttrycker. Teoriavsnittet delas in i två huvudavsnitt utifrån uppsatsens syfte och dess frågeformulering. I första avsnittet redovisas uppsatsens två nyckelbegrepp utifrån några teoretiska perspektiv på lärande, vilket förklarar elevens lärande och lärarens roll i respektive perspektiv. I det andra avsnittet redovisas karaktären hos skolmatematikens uppgifter utifrån de tidigare läroplanerna med en genomgång av de resultaten som andra forskare kommit fram till. 2.1 Några teoretiska perspektiv på lärande De tre perspektiven på problemlösning som beskrivits med prepositionerna för, om och genom kan relateras till olika pedagogiska skolor. För perspektivet relateras till stimulirespons (S – R) teorin som tillhör behaviorism. Om, genom och den aktuella läroplanens perspektiv relateras till konstruktivism. Det finns ett antal olika former av konstruktivism (svag, radikal och sociala konstruktivism) och jag anser att det är viktigt att man håller isär dem. Om perspektivet kopplas till svag- konstruktivismen som definitionsmässigt bygger på den andra av von Glasersfeld principer kognition. Genom perspektivet kopplas till socialkonstruktivism som också har olika inriktningar. Den viktigaste skillnaden är om de är individualistiska eller sociala till sin inriktning och i synnerhet om de är Piagetianska eller baserade på en samhällsorienterad teori som Vygotskijs (Engström, 1998). När jag kopplar genomperspektivet och den aktuella läroplanens teorier till social-konstruktivism ser jag de utifrån de både inriktningar, med skillnad att den aktuella läroplanen framhåller kunskapsområdet problemlösning mer utifrån kommunikativa processer. 2.2 Behaviorism Förgrundsgestalt inom behaviorismen är Skinner. Det observerbara beteende benämns inom behaviorismen respons (R). Respons föregås av händelser i miljön eller antydningar i omgivningen (”cues”). Dessa kallas stimuli (S) och ger villkoren för att ett beteende ska uppstå (Skinner, 1974). I skolans matematikundervisning har exempelvis 12 lärobokens många ”övningsuppgifter” funktionen av stimuli. Eleven reagerar på dessa och ställer upp ett sifferuttryck och räknar ut ett svar. Detta svar kontrolleras sedan mot ett ”facit” av något slag, kanske lärobokens facit eller en nick av läraren. Beteenden kan observeras exempelvis genom antal rätt lösta huvudräkningsuppgifter på en viss tid. Perspektivet är först måste man kunna, sedan kan man bygga på med (Wyndhamn et al., 2000). Enligt behaviorismen ses kunskap som någonting som kan förflyttas från en lärare till en lärande. Läraren styr och definierar vad den lärande skall uppnå. Genom övning i följder av lämpligt avpassande små steg skall eleverna lära sig vissa basfärdigheter för att sedan tillämpa dem vid lösandet av problem. Figur 1. Enligt behaviorismen ses kunskap som någonting som kan förflyttas från en lärare till en lärande. Läraren styr och definierar vad den lärande skall uppnå. (Strandvall, 2000). Den typiska dragen i behaviorismen kan sammanfattas i dessa punkter: Kunskapen är given och absolut. Kunskapen är till övervägande passivt även om den sker under programmatiska upprepande former. Eleven ses som en passiv recipient. Lärarens roll är auktoritativ, anvisade och kontrollerande (Wyndhamn et al., 2000). Sammanfattningsvis kan behaviorism metaforisk beskrivas med ett citat av Wyndhamn et al. (2000) ” Människans själsliga förmågor (”mind”) finns i en svart låda vars lock är ointressant att öppna” (s. 79). En kognitivist däremot gläntar gärna locket för att se vad som finns inne i huvudet med syftet att kunna beskriva, förklara och förstå lärandet. 13 2.3 Svag-konstruktivism (kognitivism) Wyndhamn et al. (2000) har definierat begrepp kognition enligt Nationalencyklopedin på följande sätt: De tankefunktioner med vilkas hjälp information och kunskap hämtas. Till de kognitiva funktionerna räknas varseblivning, minne, begreppsbildning, resonerande, problemlösning och uppmärksamhet. (s. 80) Den svaga konstruktivismen baseras på principen att all individuell mänsklig kunskap konstrueras av den enskilda individen. Den svaga konstruktivismen representerar ett mycket betydelsefullt steg bort från den klassiska behaviorismen. Den inser nämligen ”att vetandet är aktiv, att det är individuellt och personligt och att de bygger på tidigare konstruerad kunskap” (Engström, 1998, s. 23). I motsats till den behavioristiska psykologin, som betonar relationen mellan villkor i omgivningen (stimuli) och uppenbart beteende (responsen) vid lärandet, så studerar man i den kognitiva psykologin hur individer behandlar de stimuli de möter. Studiet av processen omfattar hur individer varseblir, tolkar och mentalt lagar den information de mottar från sin omgivning. Kunskap ses på samma sätt inom de två inriktningarna som given och absolut. I de båda skolorna används också gärna beteckning ”inlärning” med betoning på in. Kognitivismen kan emellertid förstås som en reaktion mot behaviorism då denna lämnar många frågor obesvarade om inlärning av komplexa beteenden som exempelvis språkövning och kommunikation (Wyndhamn et al., 2000). Utifrån en kognitivistisk synsätt undviker läraren att ge specifika förslag eller att bryta ner problemet i delar. Läraren hanterar diskussionen i klassrummet på ett icke styrande sätt, genom att vara ordförande, ibland frågeställare eller provokatör, aldrig domare eller bedömare (Wyndhamn et al., 2000). Läraren undervisar om Polyas modell (Polya, 1957). Vilket hjälper elever att förstå problemet, lägga upp en plan, genomföra planen och sedan titta tillbaka och värdera lösningen I den här traditionen kan man höra frågor av typen ”varför gör du så här?” och ”vad gör du?” (Riesbeck, 2000, s. 16). Sammanfattningsvis finns det alltså tre aspekter av inlärning som tillsammans bildar grunden för kognitivismen (Resnick, 1989). Inlärning ses som kunskapskonstruktionsprocess och inte som en kunskapsregistreringsprocess. Inlärning är kunskapsberoende, eftersom man använder befintlig kunskap för att skapa ny kunskap. Inlärning är mycket beroende av den situation där den försiggår. 14 2.4 Social konstruktivism Det är genom Jean Piagets inflytande att konstruktivismen har etablerats som en ledande teori om matematikinlärning. Den konstruktivistiska synen har gått längre än kognitivismen och riktar inte bara in sig på hur hjärnan behandlar information. Teorin hävdar att lärande inte kan uppfattas och reduceras till varken ett passivt formande av vissa beteenden (behaviorism) eller en helt individuell, kognitiv mental och inåtriktad process (kognitivism). Socialkonstruktivismen handlar om hur människor skapar förståelse utifrån erfarenheter och upplevelser. Elevens lärande är aktivt. Eleven bygger själv sin egen kunskap när hon bearbetar de sinnesintryck som hon får från sin omgivning. När hon konstruerar denna kunskap spelar hennes tidiga erfarenheter och kunskaper en stor roll (Engström, 1998). Kunskap kan inte överföras: Inlärningen är meningsfull då den lärande använder sig av den kunskap och de färdigheter han eller hon redan har, för att lösa realistiska problem i en realistisk kontext. Kunskap hos en människa aldrig i sin helhet kan överföras över till en annan (Jfr figur 1). Detta eftersom kunskap är resultat av en personlig tolkning av erfarenheter. Detta medför att när kunskap ”förflyttas” från en person till en annan går en del av kunskap till spillo vid översättning (Strandvall, 2000). Figur 2. Enligt den konstruktivistiska synen kan inte kunskap överföras över från läraren till de lärande, utan den skapas aktivt genom interaktion med andra jfr figu1(Strandvall, 2000) Lärarens roll i ett social-konstruktivistiskt perspektiv förklaras som en handledare. I lärarens roll ingår val av lämpliga uppgifter samt att organisera klassrumssamtal för att uppmuntra elevers matematiska förståelse. De främsta kraven för lärarens roll i detta perspektiv är: Den matematik som skall behandlas måste vara inbäddad i de utvalda problemuppgifterna. Uppgifterna måste vara tillgängliga och utmanande för eleverna samt bygga på vad de redan vet och kan göra. 15 Läraren har en mycket viktigt uppgift i att se till att de normer som finns i klassrummet verkligen uppmuntrar eleverna att lära sig på detta sätt (Lester & Lambdin, 2007). Sammanfattningsvis ser en lärare som följer idéer från den här teorin i sin undervisning sig själva i första hand som handledare. Läraren anordnar inlärningstillfällen eller problemsituationer som först aktualiserar elevernas tidigare kunskaper och sedan får eleverna att tänka vidare själva (Engström, 1998). Detta är i mottsats till kognitivismen där läraren hanterade inlärningssituation och till motsats till behaviorism där lärandet och kunskap förflyttades av läraren till eleven. 2.5 Teoretiskt perspektiv på lärande enligt Lgr 11 I inledningsavsnittet nämnde jag att en läroplan och tillhörande kursplan är tidsdokument och återspeglar vissa teorier även om det är svårt att i läroplanerna finna några tydliga konkretiseringar av och motiveringar för dem (Wyndhamn et al., 2000). För att få syn på den lärandeteori som speglar Lgr 11 s kursplan för matematik utgår jag från ett sociokulturellt perspektiv. För att se om det sociokulturella perspektivet speglar någon av kursplanen så tittade jag på kommunikativa mål som är kärnan i en sociokulturell teori. De kommunikativa målen synliggörs utifrån förmågorna som kursplanens matematik syftar till (Skolverket, 2011c). Genom att sätta problemlösningsförmåga i relation till det sociokulturella perspektivet så blir bilden tydligare av vilken lärandeteori som präglar den nu gällande kursplanen. 2.5.1 Sociokulturellt perspektiv Det är Vygotskij som ses som förgrundsgestalt för ett sociokulturellt perspektiv. Sociokulturell syn på lärande innebär att interaktionen och samspelet med andra människor är grundläggande för att tillägna sig kunskap samt etablera självförståelse och verklighetsuppfattning. Social konstruktivismen kan delas in i två olika teorier om kognition: utvecklings- och sociokulturell teori. Inom den första inriktning är det den individuella lärande som skapar förståelsen. Utvecklingen av de egna kunskaper är då huvudmålet för inlärningen. Den andra konstruktivistiska inlärningen, den sociokulturella, betonar den social konstruktion av kunskap och avvisar Piagets individualistiska teori. 16 Figur 3. Enligt sociokulturell teorin ses kunskap som en konstruktion av individens interaktion med den sociala miljön. Interaktion mellan lärare och elever samt i mellan elever (Strandvall, 2000). Kinards och Kozulin (2012) hävdar att användning av Vygotskijs socialkulturella teori i klassrummet baserar sig på begreppet lärandeverksamhet. Lärandeverksamheten kan definieras som en undervisningsform som ska göra barnet till en självgående och självstyrande lärande person. Kärnan i en lärandeverksamhetsundervisning består av tre element: Analys av uppgiften, planering och åtgärd samt reflektion. Analys och planering har en framstående plats i många pedagogiska modeller, men reflektion som ett centralt inslag i undervisningen för de yngre barnen kan med rätta betraktas som ”varumärke” för en lärandeverksamhet (Kinard & Kozulin, 2012). När man utgår från principerna för lärandeverksamhet i klassrummet övergår barnen från att endast samla information och regler till att lära sig att lära. En lärandeverksamhet har uteslutande som mål att utveckla barnet till att bli en oberoende och kritisk, lärande person. Eleverna i ett klassrum som realiserar lärandeverksamhet utvecklar en övertygelse att det är att lära sig att lära som står i centrum för deras lärande och för deras skolgång (Kinard & Kozulin, 2012). De viktiga begreppen som präglar idéerna från denna teori är reflektion, språk, som sker i kommunikativa processer som behandlas i vidare avsnittet. 2.5.2 Kommunikation Hagland, Hedrén och Taflin, (2005) har definierad den närmaste utvecklingszonen som det kunskapsområde, där en elev inte kan klara en uppgift på egen hand men kan göra det med endast litet stöd och hjälp från en kunnigare person. Eleven konstruerar sin kunskap tillsammans med andra. Vid elevens byggande av kunskap spelar studiekamrater en stor roll. När elever, som har liknande erfarenheter och kunskaper, tillsammans diskuterar ett problems lösning eller betydelsen av ett matematiskt begrepp, när de värderar och kritiserar varandra lösningar och tolkningar, då ges alla de deltagande personerna stora möjligheter att bygga på och fördjupa sina tidigare erhållna kunskaper. För17 fattarna anser att det för eleverna ligger närmare till hands att värdera och kritisera kamraternas påståenden än lärarens. Kamraterna är inte några auktoriteter på samma sätt som läraren är. Med kamraterna har eleven ett gemensamt språk och är nära sitt eget lärande Det här sagda hindrar naturligtvis inte att läraren eller andra kunniga personer kan spela en stor roll vid elevens byggande av kunskap. Genom att ställa enkla men relevanta frågor, genom att visa på hur elevens tankegångar enkelt kan utvidgas och fördjupas kan de vara ett gott stöd vid elevens lärande. 2. 5. 3 Medierande artefakter Språk: För att klara sig i världen har människan över tid skapat artefakter. Artefakter betyder produkter och verktyg. Det kan vara allt från en hammare och en skiftnyckel över en dator till ett språk (Wyndhamn et al., 2000). Språket spelar en viktig roll för utvecklingen av elevernas tänkande och lärande i matematik. Eleverna begreppsliggör deras erfarenheter tillsammans med andra genom språket. Reflektion: Enligt Kinard och Kozulin (2012) finns det tre huvudaspekter på den reflektion som ska utvecklas under de tidigare skolåren: förmåga att identifiera mål för sina och andra människors handlingar liksom metoder och medel för att uppnå dessa mål, förmåga att förstå andra människors synsätt, inklusive att betrakta objekten, processerna och problemen från andra perspektiv än det egna, förmåga att utvärdera sig själv och identifiera starka och svaga sidor av den egna prestationen 2.5.4 Lärarens roll i klassrumskommunikation En lärare som följer den sociokulturella idéer i sin undervisning i samband med klassrumskommunikation utgår från nedanstående punkterna: (Engström, 1998). Ser lärande som en problemlösande aktivitet, där elevernas egna frågeställningar och sätt att formulera problem ges ett stort utrymme. Presenterar problemlösande aktiviteter som är öppna, som stimulerar till att arbeta fram olika lösningar. Skapar en atmosfär i klassrummet som främjar utbyte av idéer. Erbjuder åtskilliga tillfällen för eleverna att tala om och framställa idéer. Underlättar organiseringen och omorganiseringen av elevgrupper för att åstadkomma lämpliga tillfällen för eleverna att ta del av information och idéer. Stimulerar eleverna till att reflektera över sina matematiska aktiviteter. 18 2.5.5 Teorin om medierade lärandeerfarenheter (MLE) Teorin om medierade lärandeerfarenheter tillhandahåller en modell för interaktionen mellan lärare, elev och uppgifter. Från att ha varit endast en källa till information och regler förväntas läraren i denna modell bli lyhörd för elevernas kognitiva behov och att utforma undervisningen/lärandet på ett sätt som främjar kognitiva funktioner och strategier för problemlösning. Läraren ska bidra till mediering. Detta innebär att lärarens roll förändras från att förse eleverna med information och regler till att bli en mediator. En av de viktigaste skillnaderna mellan dessa båda roller är att läraren inte tar elevernas kognitiva funktioner för givna, utan aktivt undersöker hur elevernas kognitiva förmåga ser ut och utformar undervisningen så att den främjar en tankemässig utveckling. Enligt författaren äger barns lärande rum i två former: direkt lärande, baserat på den vardagliga interaktionen mellan barnen och deras omgivning, och guidat lärande som är beroende av en annan människa t.ex. lärare. En mänsklig mediator väljer alltså ut, förstärker eller reducerar, upprepar, sätter in i sammanhang och tolkar omvärlden för elever (Feuerstein, 1990; refererad i Kinard & Kozulin., 2012). 2.6 En sammanfattande översiktlig jämförelse av lärandeteorier I de tidigare avsnitten har olika teorier med bäring på inlärande och beskrivning av elevens lärande och lärarens roll utifrån respektive perspektiv presenterats. Det tidigare beskrivna för perspektiv grundas på teorier av stimulus - respons typ. Behaviorismen intresserar sig ju inte för det kognitiva arbetet utan enbart ett synligt beteende. Elevens lärande ses som bildande av förbindelser eller band mellan stimuli (signaler från omgivningen) och svar eller reaktioner från någon på dessa signaler. (Wyndhamn et al., 2000). Om–perspektivet grundas i ett synsätt där lärande inte enbart ses som tillägnande av fakta, information och färdigheter, utan också lärande innebär hanterande av detta. Begreppet metakognition – omfattande bl.a. självreglering, kontroll och medveten styrning av tänkandet – ges en framträdande plats (Wyndhamn et al., 2000). Genom-perspektivet och sociokulturella perspektiv kan motiveras utifrån en konstruktivistisk idéströmning. Bärande utgångspunkter är att den lärande själv konstruerar sin kunskap och att undervisning ska beakta den lärandes tidigare existerande och strukturerande kunskap. Lärande sker också i interaktionen och samspelet med andra männi- 19 skor som är grundläggande för att tillägna sig kunskap samt etablera självförståelse och verklighetsuppfattning (Engström, 1998). 2.7 Karaktären hos skolmatematikens uppgifter Detta avsnitt inleds med en historisk genomgång av begreppet problemlösning utifrån de tidigare läroplanerna. Därefter beskrivs karaktärens hos skolmatematikens uppgifter i perspektivet för, om och genom utifrån de tidigare forskningsresultaten. 2.7.1 En historisk genomgång av begreppet problemlösning Problemlösningens placering och status i skolmatematiken har varierat över tiden. I de svenska kursplanerna levde den länge ett ganska underskymt liv för att få en central ställning som eget huvudmoment. Därför finns det inte en riktig definition av begreppet problem och problemlösning men endast ett historiskt förlopp för detta (Bergsten, 2006). Traditionellt har man ofta identifierat ”problem” med matematiska uppgifter som ska utföras. Det innebär att man till dem bl.a. hänfört också uppgifter vilkas primära syfte har varit att erbjuda träning i en viss lösningsteknik. Ofta har därtill ett problem förutsatts vara en ”textuppgift” eller en ”benämnd uppgift”, vilket har haft till följd att man ibland använt orden synonymt (Schoenfeld, 1992, s.337). I undervisningsplan för folkskolan från år 1919 återfinns termerna problem, problemlösning överhuvudtaget inte. Där talas enbart om ”uppgifter” eller ”tillämpningsuppgifter” som ska lösas. Anvisningarna till realskolans kursplan upptar likaså ”uppgifter” och ”tillämpningar” men indelar samtidigt tillämningsuppgifterna i olika typer av ”problem” exempelvis rörelseproblem, blandningsproblem (Carlgren, 1919., refererad i Wyndhamn et al., 2000). I Lgr 69 använder författarna omväxlande termerna ”problem” och ”uppgifter”, och ”tillämpningsuppgifter” förekommer också. I Lgr 69 tas även in begreppet matematisk modell. I Lgr 80 är ”problem” och ”problemlösning” högfrekventa ord. Under 1980 talet var mycket fokuset på problemlösning i sig som kognitiv och metakognitiv aktivitet med betoning på kunskaper, processer och uppfattningar. I Lgr 80 och Lpo 94 ingår problemlösning gärna samman med ”undersökande” aktiviteter. Dessutom ingår problemlösning i alla andra huvudmoment. Det betonas att problemen ska ha öppen karaktär, dvs. inte vara tillrättalagda för en viss typ av hantering. Enligt Lgr 80 ska problemet 20 också innebära en personlig, intellektuell prövning eller utmaning. Ett problem ska inte vara av rutinkaraktär och kunna lösas efter ett schablonartat mönster. Även i läroplanen från 1994 har problemlösning en kärnfunktion men ses inte längre som ett ”moment” utan ges ett mer övergripande syfte och funktion (Wyndhamn et al., 2000). Sammanfattningsvis har synen i våra läroplaner på problemlösning under årens lopp förändras. I läroplanen från 1919 sattes uteslutande procedurer mer eller mindre lika med problemlösning (”hur man ska göra”). I läroplanerna från och 1969 omnämns vissa uppgiftstyper som eleverna ska lära sig lösa efter en bestämd mall eller ett speciellt mönster – något som kan betraktas som ett procedurförfarande och ett förenklat strategiförfarande (”Vad man ska tänka”). I läroplanen från 1980 (Lgr 80) betonas med kraft att eleverna ska lära sig allmängiltiga strategier för att kunna lösa problem. Lärarna ska undervisa om problemlösning (”Hur man kan tänka”). I läroplanen 1994 är problemlösning både mål och medel för undervisning. Läraren ska undervisa genom problemlösning (”varför man ska tänka”) (Wyndhamn et al., 2000). 2.7.2. Karaktären hos skolmatematikens uppgift i för perspektivet Wyndhamn et al. (2000) har i sitt analysarbete identifierat karaktären hos skolmatematikens uppgift i för perspektivet som rutinuppgifter/standarduppgifter Nedan anges ett exempel på en rutinuppgift, samt vad skiljer sig mellan en rutinuppgift och ett problem. Rutin uppgift eller problem? Ofta brukar en problemuppgift definieras som en uppgift där man inte vet lösningen direkt utan att det finns något hinder man måste klara av. Du har 3 kritor och får 2 till. Hur många kritor har du då? inte någon problemuppgift för en sjuåring utan en rutinuppgift. Däremot är följande en problemuppgift: Moa köpte tre pinnglassar för 8.kr/st. Hur många strutar för 12 kr/st skulle hon kunna få för samma kostnad? Men om vi ger den uppgift till en elev i årskurs 6 så är det en rutinuppgift. Det som är problemuppgift för en elev kan alltså vara en rutinuppgift för en annan. (Olsson, 2008, s.1) Rutin- eller standarduppgifter definieras av Hagland et al (2005) på följande sätt: ”Rutin eller standarduppgifter är en övning som inte leder till några svårigheter för den person som löser den. Den är en uppgift som elever är bekant med och som innebär en rad färdighetsträning för henne/ honom” (s.27). I en historisk genomgång av begreppet problemlösning redovisade jag att i Lgr 69 tas även in begreppet ”matematisk modell”. Eftersom denna studie begränsas till grundsko- 21 lans tidigare år avstår jag att beskriva en matematisk modell som ingår i högstadiet enligt Lgr 69. 2.7.3 Karaktären hos skolmatematikens uppgifter i om perspektivet Wyndhamn et al. (2000) har identifierat problemets karaktär i om perspektiv som textuppgift/ benämnd uppgift/ vardagsproblem. Nedan anges ett exempel på vardagsproblem: Tidtabellen: Klockan är just nu 17 minuter i 9 och idag skall jag ta bussen till jobbet. Enligt tidtabellen är de närmaste bussavgångarna 08.49, 09.19, 09. 49 och 10.19. Vilken är den tidigaste buss jag hinner med, om det tar 15 minuter att klä mig och gå till busshållplatsen? (Löwing & kilborn, 2002, s. 248) Enligt Hagland et al. (2005) är denna typ uppgifter ”given med en text utöver eventuella matematiska symboler” (s. 27). Denna text är till för att visa på en tillämpning av matematik och/eller leda till en matematisk modell. En sådan uppgift kan vara ett problem om den uppfyller flöjlande tre villkor: • personen vill eller behöver lösa uppgiften • personen ifråga har inte en på förhand given procedur för att lösa uppgiften, och • det krävs en ansträngning av henne eller honom att lösa (Skoogh, 1986). Jämfört med för perspektivet att en rutin uppgift löstes efter en bestämd mall eller en speciell mall eller ett speciellt mönster. 2.7.4 Karaktären hos skolmatematikens uppgifter i genom perspektivet (Lester & Lambdin., 2007) har karaktäriserat rika problem som skolmatematikens uppgifter i genom perspektivet. Författaren hävder att ”Eftersom undervisning genom problemlösning startar med ett problem, så måste problemet vara så rikt att de ger eleverna möjlighet att befästa och utvidga vad de redan vet samt ge stimulans i lärandet” (s. 101). ”Rika problem innebär bland annat ett problem som bär på möjligheter till en givande diskussion av matematiska begrepp och procedurer” (Hagland et al., 2005, s. 28). Kriterier för rika problem: Problemet ska introducera viktiga matematiska idéer eller vissa lösnings strategier. Problemet ska upplevas som en utmaning, kräva ansträngning och tillåtas ta tid. Problemet ska kunna lösas på flera sätt, med olika strategier och representationer. 22 Problemet ska kunna initiera en matematisk diskussion utifrån elevernas skilda lösningar. Problemet ska kunna fungera som brobyggare mellan olika matematiska områden. Problemet ska vara lätt att förstå och alla ska ha en möjlighet att arbeta med. Problemet ska kunna leda till att elever och lärare formulera nya intressanta problem (Hagland et al., 2005, s. 28). Exempel på karaktären hos skolmatematikens uppgifter i genom perspektivet: 32 godisbitar kostar 10 kronor. Hur många bitar får du för 25 kronor? Den matematiska idé som detta problem kan leda eleverna fram till är proportionalitet i någon form. Några elever kanske nöjer sig med att fördubbla och halvera antalet bitar och motsvarande kostnad, andra kanske sätter upp en ekvation som direkt utnyttjar proportionaliteten. Åter andra elever kan tänkas använda sig av funktionslära. De kan antingen se att man för 1 krona får 32/10 bitar och att man då kan skriva: Y 3,2 där Y är antal bitar för X antal kronor, eller också inser de att en bit kostar 10/32 kronor och får då den invers funktionen Y 0,3125 , där y är kostnaden för x bitar. . Med denna korta genomgång vill Hagland et al. (2005) visa att problemet kan uppfylla villkoret att leda in eleverna på väsentliga matematiska begrepp och procedur (det första kriteriet för rika problem). För att anpassa problemet till elever som av någon anledning har svårigheter med matematik och/eller för yngre elever kan lärare agera på flera sätt. Författaren ger första några exempel på enklare varianter av problem) än den ursprungliga: 32 godisbitar kostar 10 kronor. Hur många bitar får du för 15 kronor? 23 20 godisbitar kostar 10 kronor. Hur många bitar får du för 25 kronor? 4 godisbitar kostar 2 kronor. Hur många bitar får du för 5 kronor? Man även kan presentera problem i bild eller konkret, exempelvis så här (den sista varianten av de tre exempel ovan): Figur 4. Ett exempel av rika problem. (Hagland et al., 2005). 2.8 Sammanfattning I detta avsnitt utförs en sammanfattning av hur problemlösning i avseende på elevens lärande, lärarens roll och karaktären hos skolmatematikens uppgifter beskrevs i de tidigare läroplanerna utifrån de tidigare forskningsresultaten. I Lgr 69 sågs problemlösning som målet för övrigt lärande i matematik. Läraren och eleverna arbetade med rutinuppgifter genom drill och praktiserande i små steg. Enligt detta perspektiv eleverna skulle först lära sig de enskilda aritmetiska operationerna, som sedan skulle användas i problemlösandet. Lärarens roll beskrevs som auktoritär. Elevens lärande var passivt. Nästa synsätt på problemlösning beskrevs genom undervisning om problemlösning. I Lgr, 80 blev problemlösning ett eget huvudmoment. I Lgr 80 utfördes problemlösning därefter med stegen göra upp en plan, genomföra planen och se tillbaka Karaktären hos problemet identifierades som vardagsproblem Läraren beskrevs som en ordförande. Enligt kognitivistiska idéer sågs alltså kunskap som given och absolut. Elevernas lärande innebar ”inlärning”.(Resnick, 1989). Enligt Lpo 94 såg man på problemlösning som ett medel att få eleverna att tänka matematiskt och därigenom utveckla sina kunskaper i ämnet. Läraren skulle undervisa i matematik genom problemlösning Detta förutsatte bland annat att läraren har förmåga att välja ut och använda sig av rika problem som kan få eleverna att befästa och fördjupa sina kunskaper eller upptäcka nya begrepp och samband. Läraren beskrevs som handledare och elevernas lärande var aktivt (Wyndhamn et al., 2000, Riesbeck, 2000, Hagland 24 et al., 2005, Engström, 1998, Lester & Lamdin, 2007 & Löwing & kilborn, 2002). I den nedanstående tabellen beskrivs en sammanfattning av studiens tre första nyckelbegrepp utifrån teoriavsnittet. Tabell 1. Sammanfattning av problemlösning i ett för, om och genom perspektiv: Läroplan Lgr, 1969 Lgr, 1980 Lpo, 1994 Lgr, 11 Perspektiv för om genom ? Karaktären hos rutinuppgift textuppgift rika problem skolmatematikens standarduppgift benämnd uppgift uppgifter ? vardagsuppgift överförare vägledare Lärarens roll auktoritär ordförande Elevens lärande inlärning inlärning utlärning passiv passiv aktiv 25 handledare ? ? 3. Val och motivering av metod I det här avsnittet redogör jag för hur jag har gjort och varför jag har valt att göra på detta sätt. Avsnittet delas in i tre huvuddelar: procedur, material och argumentation för etiska överväganden. Inom lärarutbildningen förekommer två olika modeller för val av undersökningsmetod, en konsumtions- och en produktionsmodell. En konsumtionsmodell kallas också för textanalys. Den är en form av examensarbete som utgår ifrån reproducerbara källor och där dessa ges status som huvudkällor för undersökningen Produktionsmodellen utgår att man formulerar ett problem som undersöks empiriskt och därefter bearbetas och analyseras (Aspelin & Sundmark, 2012). Stukat (2005) anser att när man gör sitt metodval är det viktigt att tänka på vilket syfte man har med sin undersökning. När målet med studien inte är att generalisera och få mätbara data utan istället få förståelse och kunskap för en special området är kvalitativa metoder att preferera. Eftersom min frågeställning innebär jämförelse av skrivna dokument så söker den kunskap genom en konsumtionsmodell som också kallas för ett kvalitativ inriktad textanalys. Avsikten är att genomföra en systematisk bearbetning och analys av läroplaner, i syfte att belysa den valda studiens problem och forskningsfrågan. Koncist söker denna studie kunskap genom förfarande av två olika textanalyser: Innehållsanalys ideologianalys Först utförs en kvantitativ innehållsanalys. Denna analys hjälper mig för att analysera läroplanernas struktur och innehåll. Läroplanernas struktur skiljer sig i mellan när det gäller formulering av huvudrubriker t.ex. syfte, centralt innehåll, skolans uppdrag. Avsikten med denna analys är att kunna få en helhetssyn av materialet. Helhetssynen av materialet fungerar som grund för en jämförelse där syfte är att beskriva textinnehållet på ett systematiskt sätt samt att se skillnader i innehållet. Sedan utförs en kvalitativ ideologianalys för att jämföra de fyra läroplanerna när det gäller synen på lärandet. Utifrån denna analys beskrivs sedan elevens lärande och lärarens roll i respektive perspektiv. Ideologianalys är en kvalitativ textanalys som syftar till att jämföra de idéer som en text formulerar. Det innebär att man utgår från ett specifikt perspektiv där man jämför och analyserar de förändringar som skett över en viss tid (Bergström & Boreus, 2000). När jag ska jämföra och analysera på vilket sätt den nu 26 gällande läroplanen skiljer sig åt från de tre tidigare läroplanerna gällande synen på elevens lärande och lärarens roll så innebär det att jag tittar på vilka förändringar som skett över en viss tid och därför är denna metod den mest relevanta. Utifrån de två systematiska analysen samlas studiens resultat i en tabell för att tydligt synliggöra förändringar och utvecklingar i området problemlösning med avseende på uppsatsens nyckelbegrepp vilket är det övergripande syftet för denna studie. 3.1 Datainsamling Forskningsmaterialet utgörs av reproducerbara texter (tryckta och digitala). Det material som jag samlat in består av befintliga, redan existerande dokument och texter så som läroplaner, kursplaner, utvärderingar, kommentarmaterialet och diskussionsunderlaget till kursplanen matematik. 3.2 Beskrivning av undersökningsförfarande Studiens syfte var att beskriva perspektivet på problemlösning i den aktuella läroplanen Lgr 11 med avseende på elevens lärande, lärarens roll och karaktären hos skolmatematikens uppgifter jämfört med de tidigare läroplanerna 1969, 1980 och 1994. Läroplanerna studerades med syfte att jämföra motsvarande formuleringar angående: Elevens lärande Lärarens roll Karaktären hos skolmatematikens uppgifter Eftersom respektive läroplan skiljer sig strukturmässigt gick jag genom varenda huvudrubrik för att ta reda på de rubrikerna som framställer eller förklarar studiens respektive nyckelbegrepp utifrån respektive läroplan. Detta gjorde jag utifrån en innehållsanalys. Mer förklarning angående innehållsanalys anges i analys avsnittet. Vid jämförelse har jag begränsat mig till att jämföra bara läroplanerna och kursplanerna för matematik i kunskapsområde problemlösning. Vid jämförelsen ställs konkreta citat från respektive läroplan som motsvarar samma innehåll mot varandra för att påvisa skillnader läroplanerna emellan. Perspektiven för, om och genom med avseende på de tre ovanstående punkterna beskrevs utifrån respektive läroplan och dess tillhörande lärandeteorin utifrån de tidigare forskningsresultaten. Eftersom kursplanen i matematik har i stort sett byggts utifrån avsnitt 2.2 ”Kunskaper” utgår analysen utifrån detta avsnitt (Skolverket, 2011c). Ele- 27 vens lärande och lärarens roll beskrivs utifrån Syfteavsnittet i kursplanen för matematik. Syftetexten anger de förmågorna som skolan och undervisningen ska ge eleverna (Skolverket, 2011b). En av de fem förmågorna är kunskapsområdet problemlösning. Formulering av problemlösningsförmåga i sig förklarar lärarens arbetssätt och arbetsformer så lärarens roll också förklaras utifrån syftetexten samt utifrån avsnitt 2.2 ”Kunskaper” under rubriken ”Läraren ska” (s. 14). Karaktären hos skolmatematikens uppgift framställs av ”centralt innehåll” (s, 64, 65). Eftersom alla vetenskapliga metoder kan diskuteras i termer av deras relativa styrka eller svagheter vill jag också diskutera metodens för- och nackdelar. Fördelen med den valda metoden enligt Bryman (2008) är att den är en ”öppen” forskningsmetod. Det är lätt att konkret beskriva hur man har gjort sitt urval. Det gör att metoden ofta beskrivs som en objektiv analysmetod. Metoden får ibland kritisk att det är tidskrävande med tanke att det är stora mängder material som ska analyseras och bearbetas. Det går inte heller att generalisera resultat vilket det är möjligt vid kvantitativa metoder (Stukat, 2005). 3.3 Etiska överväganden Jag har valt utifrån Vetenskapsrådet (2011) att uppfölja de forskningsetiska aspekterna som är relevant för denna studie. Anmärkningsvärt är att denna undersökning endast analyserar offentliga dokument och den därför inte behöver rätta sig efter några etiska aspekter för individen. Enligt skriften förutsätter god forskningsetiska kvaliteter av forskning som ger nya kunskaper, belyser tidigare ej kända förhållanden eller kastar ett nytt ljus över tidigare kända företeelser och relationer – den ger mer tillförlitliga kunskapskartor att navigera efter än de vi tidigare haft. Uppsatsens frågeställning fyller dessa krav. Stukat (2005) hävdar att en helt annan aspekt av etik är hur man utnyttjar andra personens skriftliga tankar. Detta diskuteras i APA-manualen där den första principen tar upp regeln om att man inte får stjäla – plagiera – andras resultat eller idéer och presentera dessa som om det vore ens egna. Eftersom mitt arbete har grundat sig på Wyndhamn et al. (2000) analysarbete har jag av hänsyn till materialet lagt stort vikt vid denna åtskillnad och tydligt beskrivit vem som säger vad eller vems idé som beskrivits. En forskningsrapport visar dålig forskningsetik om den har vetenskapliga brister när det gäller precisionen i frågeställningen, använder felaktiga metoder eller etablerade metoder på ett felaktigt sätt, systematiskt utelämnar observationer som inte passar ihop 28 med författarens tes eller använder en uppläggning av studien som inte gör det möjligt att besvara frågan. I denna studie har jag med stor medvetenhet och omsorg tagit hänsyn till de bristerna genom att följa nedanstående resonemangen. 3.3.1 Studiens tillförlitlighet All forskning syftar till att producera giltiga och hållbara resultat på ett etiskt godtagbart sätt. Denna studie är inget undantag. Frågor som rör reliabilitet, validitet och generaliserbarhet anses vara viktiga i denna studie. Reliabilitet (mättnoggrannhet, tillförlitlighet) dvs. kvaliteten på själva ”mätinstrumentet” respektive, validitet (giltighet), dvs. om jag ”mäter” det som jag avser att ”mäta” samt generaliserbarhet dvs. för vem/ vilka riktas eller gäller mitt resultat (Stukat, 2005). Utifrån litteraturen om dokumentanalys finns det några grundläggande strategier som en forskare kan använda sig av för att säkerställa den inre validiteten samt reliabilitet och generaliserbarhet. I denna studie har jag följt de kriterierna för de tre ovanstående begreppen: Utifrån flera källor: I denna studie har jag använt mig av flera relevanta källor, för att samla information på många sätt som bekräftar sedan de resultat som efterhand visar sig. Autenticitet och trovärdighet: Materialet som har samlats in för denna studie är äkta och av ett otvetydigt ursprung. Användningen av sekundärkällor för denna studie undviks så lång som är möjligt. Det används om originalverket är äldre eller svårtillgängligt (Lindhagen & Troedsson, 2011). Representativ: I denna studie har kategoriserats och analyserats utifrån två egenskaper, objektivt sätt och systematik sätt (Bryman, 2008). Den förstnämnda egenskapen betyder att mina egna personliga värderingar i så liten utsträckt som möjligt ska på verka analysen. Den egenskap som rör systematik innebär att reglerna som jag har valt för analysen tillämpas på ett konsekvent sätt för att varje form av skevhet och felkälla ska bli så liten som möjligt. Som en följd av de två egenskaper kommer förhoppningsvis var och en som använder reglerna till samma resultat. 29 4. Analys och teoretisk tolkning (utifrån Lgr11) I detta avsnitt utförs en innehållsanalys av den aktuella läroplanen samt en jämförelse av de tidigare läroplanerna. Avsikten är att tydligt markera skillnader i formuleringar mellan de fyra läroplanerna och därtill framställa uppsatsens nyckelbegrepp. I analysprocessen kommer jag ta hänsyn till två egenskaper, nämligen objektivitet och systematik (Bryman, 2008) jmf metodavsnittet. Analysen av innehållet avser relationen mellan lärarens roll, elevens lärande och problemets karaktär. Som data material används innehållet av läroplaner, kursplaner, diskussionsunderlaget och kommentarmaterialet till kursplanen i matematik. Syftet med diskussionsmaterialen är att sätta fokus på läroplanens uppbyggnad och struktur, samt visa hur den kan användas för planering av undervisning i ämnet (Skolverket, 2011c). Skolverket, (2011c) skriver att i diskussionsunderlaget finns ett antal frågeställningar som rör kursplanens syfte, centrala innehåll och kunskapskrav, läroplanens övergripande mål och deras relation till kursplanen i ämnet. Till varje kursplan finns dessutom ett kommentar material med bakgrundsresonemang och motiveringar till urval och avgränsningar i kursplanen. Diskussionsunderlagen och kommentarmaterialen är konstruerade för att komplettera varandra. Avsnittet inleds med en redovisning av den aktuella läroplanens struktur. 4.1 Struktur i den nu rådande läroplanen Den samlade läroplanen består av tre delar där de två första delarna utgörs av skolans värdegrund och samlade uppdrag samt de övergripande mål och riktlinjer som gäller för utbildningen. Läroplanen tredje del utgörs av de kursplaner och kunskapskrav som gäller för skolformen (Skolverket, 2011c). . Figur 5 illustrerar den samlade läroplanens struktur av Lgr11 (Skolverket, 2011c). 30 Kursplanen för matematik Innehåller, syfte, centralt innehåll samt kunskapskrav för godtagbara kunskaper i årskurs 3, 6 och 9. Syfte i kursplanen anger de förmågorna som skolan och undervisningen ska ge eleverna möjlighet att utveckla. Förmågorna som eleverna ska få möjlighet att utveckla anges även i långsiktiga och är också de förmågor som ligger till grund för kunskapskraven (Skolverket, 2011c). Syftetexten är formulerad så att det tydligt framgår vilket ansvar undervisningen har för att eleverna ska kunna utveckla de kunskaper och förmågor som anges (Skolverket, 2011b). 4.1.2 Förmågor Avsnittet syfte avslutas med ett antal långsiktiga mål som är uttrycka som ämnesspecifika förmågor (Skolverket, 2011a). Genom undervisning i ämnet matematik ska eleverna sammanfattningsvis ges förutsättningar att utveckla sin förmåga att: formulera och lösa problem med hjälp av matematik samt värdera valda strategier och metoder, använda och analysera matematiska begrepp och samband mellan begrepp föra och följa matematiska resonemang och, välja och använda lämpliga matematiska metoder för att göra beräkningar och lösa rutinuppgifter, använda matematikens uttrycksformer för att samtala om, argumentera och redogöra för frågeställningar, beräkningar och slutsatser. (s. 63) Citatet framhäver att kursplanen för matematik utgår utifrån fem förmågor så kallade problemlösningsförmåga, begreppsförmåga, procedursförmåga, resonemangsförmåga och kommunikationsförmåga. Nedan anges en framställning av elevens lärande i samband med problemlösningsförmåga. 4.1.3 Problemlösningsförmåga I detta kapitel utförs en analys av textinnehållet i respektive kursplan för att ta reda på elevens lärande. För att upptäcka förändringar utifrån respektive citat, samlas in de olika verben som beskriver elevernas problemlösningsförmåga. Resultatet samlas sedan in i en tabell för att belysa förändring och utveckling i elevens lärande i samband med problemlösning. Korta formuleringar som är hämtade direkt från kursplanen är genomgående kursiverade i texten. undervisning ska bidra till att eleverna utvecklar kunskaper för att kunna formulera och lösa problem samt reflektera över och värdera valda strategier, metoder, modeller och resultat. Eleverna ska även ges förutsättningar att utveckla 31 kunskaper för att kunna tolka vardagliga och matematiska situationer samt beskriva och formulera dessa med hjälp av matematikens uttrycksformer (Skolver- ket, 2011a, s. 62). Citaten framhäver att problemlösning omfattar många delar av matematiken, såsom att använda matematiska begrepp, metoder och uttrycksformer liksom att kunna resonera matematik. Det omfattar också att kunna reflektera över och värdera rimligheten i resultatet i relation till problemet. Problemlösning ska utveckla kunskaper i att tolka vardagliga och matematiska situationer och vidare kunna beskriva och formulera dessa med hjälp av matematikens uttrycksformer. Det här innebär att kunna tillägna sig det matematiska problemsituation, förklara innehållet och därefter utforma en matematisk frågeställning med hjälp av matematiska uttrycksformer (Skolverket, 2011b). Elevens problemlösningsförmåga beskrivs med följande verb enligt Lgr 11: formulera, lösa, reflektera, värdera, tolka, beskriva. I kursplanen för grundskolan 94 uttrycks problemlösningsförmåga med nästan samma formulering ”Skolan skall i sin undervisning i matematik sträva efter att eleven förstår och kan formulera och lösa problem med hjälp av matematik samt tolka och värdera lösningarna i förhållande till den ursprungliga problemsituationen” (Lpo, 1994, s. 33). Verben som har beskrivit elevens problemlösningsförmåga enligt Lpo 94 är följande: förstå, formulera, lösa, tolka och värdera. Utifrån en jämförelse av de citerade verben upptäcker vi förändringen i verben ”reflektera” och ”beskriva” Om vi återgår till teoriavsnittet och kopplar verbet reflektera till den sociokulturella teorin ser vi tydligt att det var tre element som utgjorde kärnan i lärandeverksamhet: analys av uppgiften, planering av handling samt reflektion. Analys och planering var framstående inslag i många undervisningsmodeller, men reflektion som ett centralt element i undervisningen får med rätta anses vara lärandeverksamhetens varumärke. På så sätt kan vi formulera att det övergripande förändring i elevens lärande i den aktuella läroplanen jämfört med Lpo 94 är att eleven ska kunna reflektera över och värdera rimligheten i resultatet i relation till problem. I Lgr80 formuleras elevens problemlösningsförmåga med följande formulering: ”Eleven kan förstå problemet och har en lösningsmetod. Eleven kan klara de numeriska beräkningar som krävs. Eleven kan analysera, värdera och dra slutsatser av resultaten” (s. 100). Verben som beskriver elevens problemlösningsförmåga är följande: förstå problem, lösa, analysera, värdera, och dra slutsatser av resultat. 32 Efter jämförelse finner vi tydligt att enligt Lgr 80 finns det ett färdigt matematisk problem som eleven skulle utveckla förmågan att förstå, problemet, tolka, lösa, analysera, värdera och dra slutsatser av det. Medan enligt Lgr 94 och Lgr 11 ska eleven utveckla förmågan att självständig formulera ett problem, lösa, beskriva, värdera, tolka och enligt Lgr 11 även reflektera. I Lgr 69 formuleras elevens problemlösningsförmåga under rubriken ”Huvudmoment” på följande sätt:” Problem hämtas från elevernas erfarenhetsvärld, från matematikens praktiska tillämpningar och från den matematiska teorin samt utformas så att de utvecklar elevernas förmåga att kombinera och ge uppslag” (Skolöverstyrelsen, 1969, s.138). Elevens problemlösningsförmåga förklaras med verben kombinera och ge uppslag, vilket beskriver att eleven ska lösa uppgiften samt att få ett svar, ingen problemformulering, analys och reflektion jämfört med de redan beskrivna citaten. Sammanfattningsvis konstateras att den aktuella läroplanen lägger vikten mest till de kognitiva och kommunikativa processerna så som analys, beskrivning och reflektion. I teori avsnittet upplyste jag att enligt Kinard och Kozulin (2012) finns det tre huvudaspekter på den reflektion som ska utvecklas under de tidigare skolåren jmf teori avsnittet. När eleverna utvecklar förmåga att identifiera mål, metoder och medel för handlande, kräver det skapande av ett mentalt schema för handlingen. Eleverna uppmuntras att analysera vad deras handlingar består av och använda symboliska redskap som tecken, symboler och schematiska ritningar för att representera det aktuella handlingsschemat. Genom reflektion utvecklar elevernas förmåga att förstå en annan människas synsätt som i sin tur utvecklar elevernas samarbete förmåga Under sådana aktiviteter uppmanas eleverna explicit att reflektera över den andres problemlösningsstrategier. Kinard och kozulin (2012) hävdar att en reflekterande undervisning bidrar till elevernas fördjupat matematisk tänkande. Eleven styr sin lärande på en kreativ och självständigt sätt. I en reflekterande undervisning blir eleverna till en självgående och självstyrande lärande person (Kinard & Kozulin, 2012). I tabell 2 framställs elevens problemlösningsförmåga med olika verb. I de ruterna som finns enstaka verb, markerar förändring och utveckling i elevens problemlösningsförmåga. 33 Tabell 2 visar formuleringar av verb vilka används i elevernas problemlösnings förmåga. Läroplan Citat som elevernas beskriver problemlös- 1969 1980 1994 2011 Undervisningen De grundläggande målen för ämnet matematik är att elever skall förstå och kan: Skolan skall i sin undervisning i matematik sträva efter att eleven förstå och kan: Undervisningen ska bidra till att eleverna utvecklar kunskaper för att kunna: formulera formulera Lösa lösa skall utveckla ningsförmåga med olika elevernas verb förmåga att: lösa reflektera värdera Värdera värdera Tolka tolka beskriva analysera kombinera ge uppslag 4.2 Lärarens roll enligt Lgr 11 När synen på lärande och kunskap ändras, förändras även lärarens roll som har ansvaret för att organisera och förmedla denna kunskap. I förra avsnittet gav jag upp omslag till formuleringar gällande elevens problemlösningsförmåga. Vi kom fram till att den övergripande utvecklingen i elevens problemlösningsförmåga var att eleven ska reflektera över sin lärande i problemlösningsundervisning. Utifrån förändringar i kursplanen för matematik kom vi också fram till att ”Det betydelsefulla i att eleverna utvecklar förmåga att lösa problem, använda logiska resonemang samt att kommunicera matematik med hjälp av olika uttrycksformer” (Skolverket, 2011b, s. 6) jmf inledningsavsnitt . Eftersom lärarens roll skiljer sig utifrån kunskapsområdet kommunikation i problemlösning kommer jag först beskriva kommunikationsförmåga. Därefter förklaras, vilken roll läraren har för att utveckla elevernas förmåga att kommunicera matematik med olika uttrycksformer i problemlösning. 34 4.2.1 Kommunikationsförmåga Syfte avsnittet uttrycker att: ”Undervisningen ska bidra till att eleverna utvecklar förmåga att argumentera logiskt och föra matematiska resonemang. Eleverna ska genom undervisningen också ges möjlighet att utveckla en förtrogenhet med matematikens uttrycksformer och hur dessa kan användas för att kommunicera om matematik i vardagliga och matematiska sammanhang”. (Skolverket, 2011, s. 62) Citatet framhäver att kursplanen anger att eleverna ska ges möjlighet att argumentera logiskt och föra matematiska resonemang samt att utveckla en förtrogenhet med matematikens uttrycksformer och hur dessa kan användas för att kommunicera om matematik (Skolverket, 2011b, s. 11). Att kommunicera innebär i sammanhang att utbyta information med andra om matematiska idéer och tankegångar, muntlig, skriftlig och med hjälp av olika uttrycksformer (Skolverket, 2011b). Lärarens roll i samband med kunskapsområdet kommunikation har framställts under rubriken ”Kunskaper” på följande sätt ”Läraren ska … organisera och genomföra arbetet så att eleven … får stöd i sitt språk och kommunikations utveckling”(Skolverket, 2011a, s. 14). Enligt citatet framställs lärarens roll med ett nytt begrepp, verbet ”organisera” som kan omsättas med substantivet ”organisatör”. Skolverket (2011b) skriver att i undervisning ska eleverna få möjlighet att utveckla ett allt mer precist matematiskt språk, för att därigenom kunna anpassa sina samtal och redogörelser till olika mottagare eller ändamål. Lika viktigt som att själv kunna kommunicera matematik är det att kunna lyssna till och ta del av andras beskrivningar, förklarningar och argument. För att eleverna ska kunna kommunicera matematik är det viktigt att läraren skapa en atmosfär i klassrummet som ska främja utbyte av idéer. Läraren ska underlätta organiseringen och omorganiseringen av elevgrupper för att åstadkomma lämpliga tillfällen för eleverna att ta del av information och idéer jmf teori avsnittet (Engström, 1998). Lester och Lambdin (2007) påpekar att lärarens orkestrering av klassrumskommunikation är en mycket komplex aktivitet. Förutom att avsätta rimlig tid för att diskutera problem måste läraren också avgöra vilka aspekter av problemet som särskilt skall betonas. Hur ska elevernas arbete organiseras, vilka frågor ska ställas för att elever ska utmanas med olika kunskaper? Hur ska elever stöttas utan lotsning som tar bort utmaningen? (Lester & Lambdin, 2007). Lärarens roll och uppgift i detta perspektiv blir att säkerställa att alla elever inte bara introduceras till enkla matematiska operationer utan omfattar även ett ansvar för att alla elever ges förutsättningar att tillägna sig sådana tan35 keredskap som gör det möjligt för dem att självständigt utforska olika matematiska problem. Undervisning behöver i detta perspektiv organiseras så att eleverna både introduceras i matematiska verksamheter och lär sig använda olika slags tankeredskap för att fördjupa matematiskt arbete (Kinard & Kozulin, 2012). Detta innebär att lärarens roll förändras från att förse eleverna med information och regler till att bli en mediator jämfört med de tidigare perspektiven. En av de viktigaste skillnaderna mellan dessa båda roller är att läraren inte tar elevernas kognitiva funktioner för givna, utan aktivt undersöker hur elevernas kognitiva förmåga ser ut och utformar undervisningen så att den främjar en tankemässig utveckling jmf teoriavsnittet. 4.3 Karaktären hos skolmatematikens uppgifter enligt Lgr 11 I detta avsnitt beskrivs karaktären hos skolmatematikens uppgift utifrån ”centralt innehåll” i kunskapsområdet problemlösning: ”Strategier för problemlösning i vardaglig situationer och inom olika ämnesområden samt värdering av strategier och metoder. Matematisk formulering av frågeställning utifrån vardagliga situationer och olika ämnesområden. Den aktuella läroplanen, Lgr 11, definierar matematiska problem som ”situationer eller uppgifter där eleverna inte på förhand känner till hur problemet ska lösas. Istället måste de undersöka och prova sig fram för att finna en lösning” (Skolverket, 2011b, s. 9). Matematiska problem kan då också beskrivas som uppgifter som inte är av rutinkaraktär. Oftast förekommer ett problem i en konkret situation som gör att eleverna behöver göra en matematisk tolkning av situationen. Ibland är problemen inommatematiska och saknar då direkt anknytning till en vardaglig situation. Problem kan ha kopplingar till olika matematiska kunskapsområden och kan ta sin utgångspunkt i egna intressen, fantasier eller verkliga situationer. Ett matematiskt problem kan betraktas som en relation mellan eleven och hur långt eleven kommit i sin kunskapsutveckling. En elev som har kommit långt i sin kunskapsutveckling kan uppleva en uppgift som en rutinuppgift om hon eller han känner till en lösningsmetod. En annan elev kan i mötet med samma uppgift däremot behöva undersöka och pröva sig fram till en lösning (Skolverket, 2011b). 36 De olika matematiska kunskapsområden kan kopplas till de fem förmågorna som kursplanens matematik syftar till. De fem förmågorna integreras genom att eleverna ska utbyta information med andra om matematiska idéer och tankegångar, muntligt, skriftligt och med hjälp av olika uttrycksformer (Skolverket, 2011b). Ett exempel på att eleverna kommunicerar matematik med olika uttrycksformer är fyrfältsblad. Ett fyrfältsblad innebär att man förtydligar en matematisk problemlösningsuppgift och arbetar med problemet utifrån olika sätt att presentera och lösa problemet (Andersson, 2010). En estetisk lösning (lek, drama, bilder, laborativ material). En logisk lösning (ord, samtal, resonemang). En numerisk lösning (matematiska beräkningar). En symbolisk lösning (formler och generaliseringar). Andersson hävdar att forskning visar att de elever som lyckas bra är elever som i hög grad reflekterar över sin lärandeprocess. De blir själva motorn i sitt eget kunskapsprojekt. 1. 2. 3. 4. Vad gjorde jag? (estetisk lösning) Hur tänkte jag och vad sa jag? (logisk lösning) Hur räknade jag? (numerisk lösning) Vad är detta för matematik? (symbolisk lösning) 37 Ett exempel på fyrfältsblad ESTETISK LÖSNING LOGISK LÖSNING Bönspelet. Likhetstecknets betydelse. Spelplanen såg ut så här: Har eleverna svårt att förstå varför de inte skulle räkna ut något när det fanns ett likhetstecken? Har de svårigheter med hur de skulle anEleverna ska komma fram till hur många gripa problemet? bönor det finns i asken. t Kan vi göra det enklare för dem? Kan de hitta på egna liknande problem? NUMERISK LÖSNING SYMBOLISK LÖSNING 5 = 3+ _ 5 3 x 12 + 8 = 3 + __ 12 8 3 x 15 - __ = 7 + 2 15 x 7 2 x 16 8 y _ + 16 = 8 + _ Figur 5 Ett exempel på fyrfältsblad.(Andersson, 2010). Sammanfattningsvis kan karaktären hos skolmatematikens uppgift enligt Lgr 11 förklaras som vardagliga problem, uppgifter som inte är av rutin karaktär med skillnad i för perspektivet. och Problem som kan ha kopplingar till olika matematiska kunskapsområden. Den sistnämnda fyller kriterierna för rika problem enligt Hagland et al. (2005). 38 5. Diskussion Avsikten med denna studie var att undersöka och ta reda på perspektivet i problemlösning i matematik med avseende på elevens lärande, lärarens roll och problemets karaktär enligt den aktuella läroplanen Lgr11 jämfört med de tidigare läroplanerna i 1969, 1980 och 1994. Avsikten med att undersöka studiens syfte var att ge uppslag till diskussion rörande förändringar och utvecklingar av undervisning i matematik i problemlösning. Det övergripande syfte med denna diskussion var att behandla vilka konsekvenser man får i samband med undervisning i matematik utifrån respektive perspektiv och hur dessa konsekvenser påverkar lärarprofession samt eleverna i skolan. I inledningsavsnittet nämnde jag att genom att synliggöra förändringar och utvecklingar i området problemlösning utvecklas och reflekteras en bättre förståelse och medvetenhet i matematikundervisning. Detta i sin tur bidrar till att förbereda eleverna för kommande studier och livet utanför skolan vilket är ett av de övergripande syftena med problemlösning enligt samtliga läroplaner. Dessa två mål är naturligt relaterade till varandra eftersom förståelse uppnås bäst med problemlösning (Lester & Lambdin, 2007). Utifrån de ovanstående motiveringarna anser jag att denna forskning har en stor betydelse i matematikundervisning samt för min egen medvetenhet av synen på elevens lärande och min roll som blivande matematik lärare. Uppsatsens frågeställning besvarades genom att genomföra av en kvalitativ textanalys som metodval vilket var en relevant metod för denna studie med anledningen att metoden besvarade studiens frågeställning. Svårigheterna som jag kämpats med under studiens gång var brist på att hitta relevanta data för uppsatsens frågeställning som ansets vara relativt outforskad. Det var också svårt att hitta de äldre originalverken såsom ”folkskolan från år 1919”. 5.1 Koppling till frågeställning och resultat I detta avsnitt redovisas resultatet på studiens frågeställning. Studiens frågeställning handlade om ur vilket perspektiv problemlösning framställs med avseende på elevens lärande, karaktären hos skolmatematikens uppgifter och lärarens roll i den aktuella läroplanen Lgr 11 jämfört med läroplanerna i 1969, 1980 och 1994. Elevens lärande: Analysavsnittet rapporterar att den nuvarande kursplanen (Lgr 11) ser problemlösning som en motor eller drivkraft i lärande. Perspektivet på problemlös- 39 ning är byggd utifrån den sociokulturella teorin. Där eleven beskrevs som en aktiv kritisk tänkande person. För elevens lärande används uttrycket ”lära sig att lära”. Den övergripande utveckling i elevens lärande jämfört med de tidigare perspektiven var att den reflekterande eleven var i sin lärande självgående och självreglerande och sågs som en skapare, en kreatör och framförallt som en frambringare. Lärarens roll: lärarens roll enligt den aktuella läroplanen beskrevs som en mediator och organisatör jämfört med de tidigare perspektiven som läraren i sin roll förklarades som en handledare, vägledare och auktoritär. Enligt den aktuella läroplanen förändrades lärarens roll från att överföra, förmedla, handleda information och regler till att vara resurs för medierade lärandeerfarenheter. En av de viktigaste skillnaderna mellan dessa båda roller är att läraren inte tar elevernas kognitiva funktioner för givna, utan aktivt undersöker hur elevernas kognitiva förmåga ser ut och utformar undervisningen så att den främjar en tankemässig utveckling. Karaktären hos skolmatematikens uppgifter: När det gäller karaktären hos skolmatematikens uppgifter betonar den nuvarande kursplanen tydligt att problemet inte ska vara av rutin karaktär utan eleven ska utbyta information med andra om matematiska idéer och tankegångar, muntligt, skriftligt och med hjälp av olika uttrycksformer. I tabell 3 har jag framställt sammanfattning av resultatet på studiens frågeställning med avseende på studiens nyckelbegrepp. 40 Tabell 3 visar resultat på perspektiven på problemlösning med avseende på elevens lärande lärarens roll och karaktären hos skolmatematikens uppgifter, utifrån de tidigare läroplanerna samt enligt den aktuella läroplanen Lgr 11. Sammanfattning av resultat avsnittet läroplan Lgr, 1969 Lgr, 1980 Lpo, 1994 Lgr, 11 perspektivet För om Genom i Karaktären rutinuppgift textuppgift rika problem hos standardupp- benämnd gift uppgift vardagsproblem skolma- tematikens uppgifter uppgifter som inte är av rutinkaraktär vardagsproblem rika problem mediator Lärarens roll Elevens rande auktoritär lä- inlärning ordförande handledare inlärning lärandet är ak- kreativt lärande organisatör lärandet är pas- lärandet är pas- tivt sivt sivt Utifrån de ovanstående förändringarna ser jag att den rådande läroplanen lägger ett nytt perspektiv på problemlösning. Jag föreslår att det nya perspektivet kan beskrivas med prepositionen i. Enligt resultatet av denna studie ska läraren undervisa i problemlösning i matematik. 5.2 Slutsats Utifrån studiens syfte vill jag ha en genomgående diskussion kring uppsatsens resultat för att komma fram till en formulering av studiens slutsatser. Resultatet som kommit fram från för perspektivet rapporterar att eleverna först lärde sig de enskilda aritmetiska operationerna som senare kunde användas i problemlösandet (Wyndhamn et al., 2000). Uppgifterna som eleverna arbetar med kom framför allt från 41 läroboken. Dessa är i huvudsak korta, saknade kontext och är symboltyngda (Lester et al., 2007). Denna problematik enligt Kinard och Kozulin (2012) bidrar till att eleverna inte är fördjupat engagerade i ett arbete med att utveckla och behandla djupare strukturer i sitt tänkande och känner sig inte heller utmanade att utifrån sina erfarenheter och grundläggande kunskaper skaffa sig den förståelse som behövs för att åstadkomma de underliggande abstraktionerna och generaliseringarna i matematik. Således avslutar många elever sina kurser i matematik med en illusorisk kompetens grundad på upprepning av memorerat stoff (Kinard & Kozulin, 2012). Vidare påpekar författarna att eleverna inte bygger upp den förståelse eller den flexibla struktur som krävs för äkta lärande och för bildande av ny kunskap i olika sammanhang och situationer. Dessa ytliga erfarenheter är inte meningsfulla, främjar inte någon kunskapsutveckling i matematik, konsekvenserna enligt författaren blir till att flera elever hoppar av sin utbildning i matematik. Vi ser att perspektivet på problemlösning i Lgr 11 vill ändra situationen som den beskrivs av Kinard och Kozulin (2112). Lester och Lambdins (2007), påstående kommer också överens med Kinards och Kozulins (2012). Författarna hävder att: olyckligaste konsekvensen med en traditionell undervisning är att eleverna även i bästa fall lämnar skolan med bara en uppsättning av fakta, procedurer och formler som förstås på ett ytligt och osammanhängande sätt. Kanske är värre är att de knappast kommer att ha en aning om hur det de lärt sig kan användas utanför skolan. (Lester et al., 2007, s. 97) Möllehed (1993) påpekar att man idag löser de problem, som finns i klassens lärobok och som oftast är rutinartade eller följer en på förhand visad lösningsmodell. Författarens påstående stämmer överens med mina egna erfarenheter och upplevelser om problemlösningsundervisning under min egen skolgång samt den verksamhetsförlagda tiden och även med de utvärderingarna som redovisades i inledningsavsnittet. Lester et al. (2007) betonar att idag leder enighet bland ledanda matematikutbildare om att problemlösningens roll i skolmatematiken bör få en ny karaktär. Idag är problemlösning ofta en aktivitet som kommer efter att eleverna studerat begrepp och färdigheter. Istället bör problemlösning betraktas som ett hjälpmedel för att utveckla nya kunskaper i matematik. Vi ser tydligt att det är många forskare som anser att för perspektivet ska förändras och utvecklas. Det resultat som kommit fram från om perspektivet var att eleverna på egen hand skulle klara av att hitta en lämplig lösningsstrategi till de uppgifterna som ställs i mate- 42 matikundervisningen. Läraren skulle hantera diskussion i klassrummet på ett icke styrande sätt. Eftersom om perspektivet lämnade många frågor obesvarade om inlärning som exempelvis språkövning och kommunikation sågs elevens lärande i detta perspektiv passiv. Det är därför om perspektivet ska byggas enligt den rådande läroplanen som lägger stor vikt på kommunikativa processer och betonar att eleverna ska få stöd i sitt språk och sin kommunikationsutveckling. Det resultatet som kommit fram utifrån genom perspektivet på problemlösning påpekar att problemlösning ses mer som ett medel att få eleverna att tänka matematiskt och därigenom utveckla sina kunskaper i ämnet (Wyndhamn et al., 2000). Engström, Engvall och Samuelsson (2007) hävdar att i Lpo 94 diskuteras problemlösning som en viktig aspekt av matematikundervisningen. De positiva konsekvenserna blir att eleverna inte endast lär sig matematik för att hantera vardagen utan de också lär sig matematik därför att de ska bli duktigare i matematik. Eftersom genom perspektivet lämnar frågorna som rör begreppet reflektion bör detta perspektiv granskas enligt den nya läroplanen som betonar att eleverna ska reflektera över och värdera rimligheten i resultatet i relation till problemet . Det resultatet som kommit fram utifrån i perspektivet rapporterar att den nuvarande kursplanen (Lgr, 11) för matematik ser problemlösning som en motor eller drivkraft i lärande, (Skolverket, 2011). I ett Vygotskianskt perspektiv betonas undervisningsform som ska göra barnet till en självgående och självreglerande lärande person. Kärnan i en lärandeverksamhet består av tre element: Analys av uppgiften, planering och åtgärd och reflektion speciellt språket och språkandet som resurs för utvecklingen av elevers matematiska tänkande. Sociokulturella perspektiv på lärande och kunskap har lett till en ökad betoning på att se allt lärande som bundet till specifika praktiker och att se lärandet som en fråga om att bli allt mer förtrogen med sådana praktiker (Kinard & Kozulin, 2012). För matematiskt lärande får detta konsekvenser även för undervisningens utformning. Eleverna får möjlighet att delta i innehållsligt rika matematiska verksamheter och få tillgång till matematiska redskap och guidas i användning av dem för att kunna utveckla en självständig problemlösande hållning. Undervisningen i problemlösning således ger eleverna möjlighet att lära tänka och tala ”matematiska”. Lärarens roll och uppgift i detta perspektiv blir att säkerställa att alla elever inte bara introduceras till enkla matematiska operationer utan omfattar även ett ansvar för att alla elever ges förutsättningar att tillägna sig sådana tankeredskap som gör det möjligt för dem att självständigt utforska olika matematiska problem. Undervisning behöver i detta 43 perspektivorganiseras så att eleverna både introduceras i matematiska verksamheter och lär sig använda olika slags tankeredskap för att fördjupa matematiskt arbete (Kinard et al., 2012). Sammanfattningsvis visar undersökningen att i perspektivet betraktar problemlösningsförmåga och -tänkande som ett sätt att ställa upp hypoteser, ge förklarningar och skapa motiveringar. Vilket är matematikundervisningens mål och syfte (Kinard & Kozulin, 2012). Mina slutsatser framhäver att för perspektivet ska förändras, om perspektivet ska byggas vidare och genom perspektivet ska granskas och utvecklas enligt den aktuella läroplanen. Vi som dagens lärare ska utveckla vissa matematiska färdigheter för problemlösning i för perspektivet. Lärande behöver inte uppfattas som och reduceras till varken ett passivt formade av vissa beteenden (behaviorism) eller en helt individuell, kognitiv, mental och inåtriktad process (kognitivism). Lärande kan också uppfattas som ett socialt fenomen som medieras av språket i sociala diskurser (sociokulturellt perspektiv) (Wyndhamn et al., 2000). 5.3 Förslag till fortsatt forskning I min studie har jag genomfört en textanalys metod där jag beskrev problemlösning perspektiv med avseende på relation mellan problemets karaktär, lärarens roll och elevens lärande utifrån en studie av de tidigare läroplanerna 1969, 1980, 1994 och den aktuella 2011. Det vore intressant med en empirisk undersökning där man skulle undersöka i vilket perspektiv dagens lärare undervisar problemlösning i matematik, vilket eller vilka typer av problem som använts i undervisning och hur elevens lärande ses i relation med lärarens arbetssätt och arbetsformer. Man ska observera undervisning, intervjua lärare och analysera undervisningsmaterial. Bryman (2008) anser genom att använda flera källor och metoder för sin beskrivning kan vara ett tänkbart och lämpligt tillvägagångssätt för att få ett område belyst på ett mer allsedigt sätt. Genom en empirisk undersökning syns och granskas tydligt relation mellan lärarens roll, problemets karaktär och elevens lärande. Det som skulle vara intressant är att se i vilket streck resultatet från den empiriska undersökningen kommer överens med min kvalitativa textanalys eller med andra ord, i vilken utsträckning Lgr11 förverkligas i matematikundervisningen. 44 6. Referenser Ahlström, R., Bergius, B., Emanuelsson, G., Emanuelsson, L., Holmqvist, M., Restedt, E., & Wallby, K. (2009). Matematik ett kommunikationsämne. Göteborg: Nämnaren. Andersson, L. (2010). Fyrfältsblad, Pre- algebra. Malmö: Malmöhögskola. Tillgänglig på Internet: https://mah.itslearning.com/main.aspx?CourseID=7261 (Hämtat 2013 05.09). Aspelin, J & Sundmark, B. (2012). Examensarbetets former. Text/dokument - studie. Malmö: Malmöhögskola. Bergsten, C. (2006). En kommentar till den matematiska problemlösningsdidaktiken. I L Häggblom, m.fl. Perspektiv på kunskapens och läromedel villkor (s. 165-176). Vasa: Akademi. Bergström, Göran & Boréus, Kristina. (2000). Textens mening och makt: metodbok i Samhällsvetenskaplig textanalys. Lund: Studentlitteratur. Bryman, A. (2008). Samhällsvetenskapliga metoder. Malmö: Liber. Engström, Arne (red.). (1998). Matematik och reflektion. Lund: Studentlitteratur. Engström, A, Engvall, M & Samuelsson J. (2007). Att leda den tidiga matematikundervisningen. Linköping: Linkoping universitet. Eriksson, I. (2009). Re-interpreting teaching: A divided task in self-regulated teaching practices. Scandinavian journal of Educational Research, 53 (1), P. 53-70. Hagland, K, Hedrén, R & Taflin, E. (2005). Matematiska problem. Stockholm: Liber. Kinard, J & Kozulin, A (2012). Undervisning för fördjupat matematiskt tänkande. Lund: Studentlitteratur AB. Lester, F & Lambdin, D. (2007). Undervisa genom problemlösning. I Jesper Boesen, Göran Emanuelsson, Anders Wallby & Karin Wallby (red.), Lära och undervisa i matematik – internationella perspektiv (s.95-108). Göteborg: Nationellt Centrum för matematikutbildning, NCM. Skolöverstyrelsen. (1969). Läroplan för grundskolan Lgr 69. Allmän del (del I). Stockholm: Liber AB. Skolöverstyrelsen. (1980). Läroplan för grundskolan Lgr 80. Stockholm: Liber Utbildningsförlaget. Utbildningsdepartementet. (1994). Läroplan för det obligatoriska skolväsendet Lpo 94. 45 Möllehed, E. (1993). Problemlösning I matematik I grundskollärarutbildningen. Utvecklingsarbete 3. Lund: Lund universitet. Löwing, M & Kilborn, W. (2002). Baskunskaper i matematik. Lund: studentlitteratur. Olsson, I. (2008). Att lyckas med problemlösning – huvudmålet i grundskolans matematik. Biennal, (311).s, 1. Hämtad http://ncm.gu.se/media/biennal/- dokumentation/2008/resources/file/311.pdf (2013-04-12). Polya, G. (1957). How to solve it. Second Edition. Princeton: Princeton University press. Resnick, L. (1989). Introduktion ingår i L. Resnick (red.). Knowing learning, and instruction Essays in honour of Robert Glaser (s. 1- 24) Hillsdale, NJ: Lawrence Erlbaum. Riesbeck, E. (2000). Interaktion och problemlösning. Att kommunicera om och med matematik. Linköping: Linköpings universitet. Lindhagen, A & Troedsson, A. (2011). Hur skriver jag? En introduktion till APA stilen. Lund: Lunds universitet. Schoenfeld, A. (1992). Learning to think mathematically: Problem Solving, Met cognition and Sense Making. In D. Grows (Ed). Handbook of Research in Mathematics Teaching and Learning. New York: Macmillan publishing Company (pp.334370). Svenska Utbildnings förlaget Liber AB. Skinner, B. F. (1974). About behaviorism. New York: Knopf. Skolverket. (2006). Med fokus på matematik och naturvetenskap. En analys av skillnader och likheter mellan internationella jämförande studier och nationella kursplaner. Västerås: Edita. Skolverket. (2011a). Läroplan för förskolan, förskoleklass och fritidshemmet 2011. Västerås: Edita. Skolverket. (2011b). Kommentarmaterial till kursplanen i matematik. Västerås: Edita. Skolverket (2011 c) Diskussionsunderlag till kursplanen i matematik.Tillgänglig på internet: http://www.skolverket.se/publikationer?id=2538(2013-05-01). Skoogh, L. (1986). Kunskaper och färdigheter: Problemlösning viktigaste huvudmomentet i Lgr 80. Nämnaren (2-3) 22-23. Hämtad från http://ncm.gu.se/pdf/namnaren/2223_86-87_2-3.pdf Strandvall, T. (2000). Inlärningsteorier och tillämpningar: Avhandling för pedagogik Magisterexamen. Åbå Akademi pedagogiska fakulteten institution för lärarut- 46 bildning: Vasa. Tillgänglig på internet: http://www.vasa.abo.fi/users/tstrandv/kapitel21.htm (hämtat 04.05.2013). Stukat, S. (2005). Att skriva examensarbete inom utbildningsvetenskap. Lund: Studentlitteratur. Vetenskapsrådet (2011). Forskningsetiska principer inom humanistisk- samhällsvetenskaplig forskning (2011). Stockholm: Vetenskapsrådet. Tillgänglig på Internet: http://www.cm.se/webbshop_vr/pdfer/2011_01.pdf (2013-02- 22). Wyndhamn, J, Riesbeck, E & Schoultz, J. (2000). Problemlösning som metafor och praktik. Linköping: Linköping University. 47