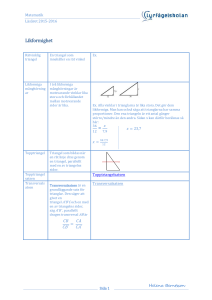
Nisse Bärs problem 4
Problemet bestod i att finna maximala storleken, radien r, på tre identiska klot som placeras
inuti ett större klot med radien R.
Om man bildar ett plan genom de tre mindre klotens medelpunkter kan problemet reduceras
till ett två-dimensionellt problem enligt figuren nedan.
Sammanbinds de tre mindre klotens/cirklarnas mittpunkter erhålls en liksidig triangel med
sidan 2r. Alla toppvinklar i en liksidig triangel är 60˚ vilket i triangeln med tjocka linjer ger
den spetsiga vinkeln 30˚. Med hjälp av denna triangel erhålls sambandet:
( R – r ) x cos30˚ = r
__
Eftersom cos30˚ = √ 3 / 2
__
(R–r)x√3 / 2 = r
erhålls sambandet:
Ù
__
(R/r –1)x√3 / 2 = 1
Ù
__
R/r = 1 + 2/ √3
Ù
__
__
r/R = √3 / (√3 +2)
30˚
≈ 1,732 / 3,732 ≈ 0,464
