Kap 1 Taluppfattning

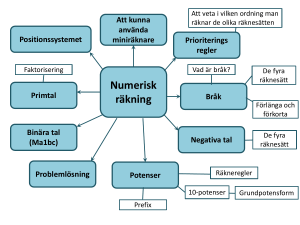
Kap 1 Taluppfattning
Prioriteringsregler
Beräkningar ska utföras i följande ordning:
1. innehåll i parenteser
2. multiplikation och division
3. addition och subtraktion
Följande exempel visar ordningen:
Räkning med negativa tal
Då man adderar eller subtraherar med ett negativt tal, så ersätter man de två tecken som
”står som grannar” med ett enda tecken enligt följande exempel:
5  (3)  5  3  8
5  (3)  5  3  2
Regeln kan sammanfattas ”lika tecken ger plus och olika tecken ger minus”
Då man multiplicerar eller dividerar med negativa tal gäller samma regel:
”då talen har lika tecken blir resultatet plus och då talen har olika tecken blir resultatet
minus”
Ex:
(3)  (5)  15
3  (5)  15 ;
(3)  5  15
Rationella tal
Ett bråk är en kvot mellan två heltal, där nämnaren inte kan vara noll. Detta kallas också för
ett rationellt tal.
Varje bråk kan skrivas om till andra bråk, med nya värden i täljare och nämnare, genom att
man multiplicerar täljaren och nämnaren med samma tal, man förlänger bråket. Det nya
bråket får samma värde som ursprungsbråket!
Ex:
2 24 8


3 3  4 12
;
Både
2
8
och
har samma värde som decimaltal  0, 666666
3
12
Man kan även förkorta ett bråk, vilket betyder att man dividerar både täljare och nämnare med
samma tal.
Ex:
8
8/ 2 4


;
10 10 / 2 5
Både
8
4
och
har värdet 0,8 som decimaltal!
10
5
Då man adderar eller subtraherar bråk med varandra måste bråken ha samma nämnare!
Om så inte är fallet, måste ett eller flera bråk förlängas så att de får samma nämnare.
Ex:
3 3
6
3
9

 
 ;
5 10 10 10 10
(
3
förlängdes med talet 2!)
5
Då man multiplicerar bråk med varandra, multipliceras täljarna med varandra och nämnarna
med varandra.
Ex:
Då ett heltal och ett bråk multipliceras, ”gångras” heltalet med täljaren! Se exemplet nedan!
=
Vid division av bråk, kan divisionen göras om till en multiplikation om man multiplicerar
bråket i täljaren med det inverterade talet till bråket i nämnaren!
(Att invertera ett bråk betyder att man byter plats på täljare och nämnare!)
Ex:
=
Tiopotenser och grundpotensform
Vårt sätt att skriva tal är med basen 10. Det betyder att varje position, plats, i ett tal har ett
visst värde som är en potens av 10.
En tiopotens är en potens med tio som bas och ett heltal som exponent:
10 000 = 105, 1000 = 103, 1 = 100, 0,01 = 10-2 osv.
T ex i talet 573 står femman på positionen för hundratal, 5·
7·
, och trean på positionen för ental, 3·
, sjuan på positionen för tiotal,
Alla tal kan skrivas i s k grundpotensform, vilket är särskilt praktiskt då man skriver riktigt
små och riktigt stora tal.
Ett tal skrivet i grundpotensform består av en multiplikation mellan ett tal mellan 1 och 10,
samt en tiopotens.
Ex:
25 000 = 2,5·104
565 000 000 = 5, 65·108
0,00 075 = 7,5·10-4
0,000 000 009 = 9·10-9
Ett kommatecken placeras i talet så att man får ett tal mellan 1 och 10. Det antal steg du
”flyttar kommat”, blir talet som står i exponenten i tiopotensen. För ett tal som ursprungligen
är mindre än 1, får vi ett negativt tal som exponent.
Primtal och delbarhet
Primtal kallas de tal som endast kan delas med sig själv och med siffran 1.
Ex: 3, 7, 11, 19.
T ex 9 och 15 är inte primtal, eftersom 9 kan delas med 3 och 15 kan delas med 3 och 5.
- Är 23 ett primtal?
Alla tal som inte är primtal kan skrivas som en produkt (=resultat av en multiplikation) mellan
två eller flera primtal. Börja med att dela med något tal som du kan, sedan delar du vidare!
T ex 48  4  12  2  2  2  6  2  2  2  2  3
16  2  8  2  2  4  2  2  2  2
Alla tal som ett visst heltal kan delas med, kallas för multipler av heltalet.
T ex talet 28 kan delas med 1, 2, 4, 7, 14 och 28 – dessa tal är multiplar av 28!
- Vilka multiplar har talen 24 och 70?
Delare till ett tal
Om du ska bestämma alla delare till ett tal, så börjar du med att dela upp talet i primtal! Sedan
ska alla kombinationer av primtalen multipliceras med varandra för att hitta samtliga delare!
Vi tar ett exempel – vilka tal är delare till talet 936?
Primtalsuppdelning: 936  2  468  2  2  234  2  2  2  117  2  2  2  3  39  2  2  2  3  3 13
Alla kombinationers produkter:
Två siffror
Tre siffror
222  8
22  4
23  6
2  2  3  12
2  13  26
2  3  3  18
3  13  39
2  2  13  52
2  3  13  78
3  3  13  121
Fyra siffror
2  2  2  3  24
2  2  3  3  36
2  2  2  13  104
2  2  3  13  156
2  3  3  13  234
Fem siffror
Alla dessa produkter, 18 st tal, samt 936 själv, kan man dividera talet 936 med!
(I kombinationerna kan det ingå upp till 3 st tvåor, 2 st treor och 1 tretton, enligt
primtalsuppdelningen.)
Då man delar upp ett tal i primtal, kan det vara bra att ha koll på följande delbarhetsregler:
Ett tal är alltid delbart med…
2
3
4
5
6
8
9
…om
det är ett jämnt tal
dess siffersumma är delbar med 3
talets sista två siffror kan delas med 4
talet slutar på 0 eller 5
talet är delbart med både 2 och 3
talets sista tre siffror kan delas med 8
dess siffersumma är delbar med 9