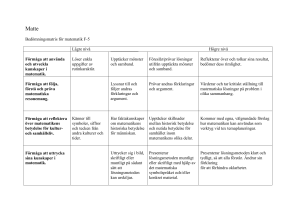
Problemlösning i matematik är inte oproblematiskt

Malmö högskola
Lärande och samhälle
Natur, miljö, samhälle
Examensarbete
15 högskolepoäng
Problemlösning i matematik är inte
oproblematiskt: Fyra lärare ger sin syn
Problem solving in mathematics is not unproblematic: Four
teachers are giving their view
Dusko Diko
Altin Musa
Lärarexamen 270 hp
Examinator: Nanny Hartsmar
Matematik och lärande
Handledare: Maria C. Johansson
Förord
Examensarbetet har genomförts under höstterminen 2013 under vår sista termin på
lärarutbildningen vid Malmö högskola. Vi utbildar oss till matematiklärare för grundskolans
senare år samt gymnasiet. Under arbetets gång har samtliga delar gjorts i samarbete mellan
oss båda. Detta har vi gjort för att på bästa sätt försäkra oss om att bådas erfarenheter,
kunskaper, idéer och synpunkter kommer arbetet till del.
Som stöd har vi haft vår handledare Maria C. Johansson som vi fått enorm hjälp av. Idéer har
bollats fram och tillbaka. Vi vill även tacka våra lärare som hjälpt oss med arbetet genom att
ställa upp på intervjuerna.
Malmö 28 oktober 2013
Dusko Diko och Altin Musa
2
3
Sammanfattning
I vår undersökning har vi intervjuat fyra lärare med avseende på hur de ser på problemlösning
och hur de arbetar med det. Lärarna arbetar i två olika skolformer, kommunal skola och
internationell skola i Sverige. Därför följer skolorna olika läroplaner. Anledningen till att vi
valt att ta med båda skolformerna är för att vi upplevt en högre motivation för problemlösning
i den internationella när vi tidigare haft kontakt med dem. Vi har analyserat deras svar med
hjälp av ett analytiskt ramverk som tar till hänsyn fyra lärandeteorier som kan sägas haft
påverkan på lärandet i skolan. Teorierna är behaviorism, kognitivism, konstruktivism och
sociokulturell teori. Vi har även jämfört lärarna med varandra för att försöka hitta skillnader
och likheter.
Det vi kom fram till i undersökningen var att de lärare vi intervjuat skiljer sig något i hur
de ser på problemlösning. Likaså varierar deras arbetssätt med problemlösning med både
likheter och skillnader. Resultatet gör det svårt att förklara varför vi upplevde en högre
motivation i den internationella skolan utifrån lärarnas syn på och undervisning med
problemlösning, utan möjligheten finns att det är andra faktorer som påverkar.
Nyckelord: Matematik, problemlösning, lärandeteorier, behaviorism, kognitivism,
konstruktivism, sociokulturella teorin, analytiskt ramverk, internationell skola, kommunal
skola
4
5
Innehållsförteckning
Förord ...................................................................................................................................................... 2
Sammanfattning....................................................................................................................................... 4
1. Inledning.............................................................................................................................................. 8
1.1 Syfte .............................................................................................................................................. 9
1.2 Frågor ............................................................................................................................................ 9
2. Bakgrund och tidigare forskning ....................................................................................................... 10
2.1 Läroplanerna................................................................................................................................ 10
2.1.1 Lgr 11 ................................................................................................................................... 10
2.1.2 International Baccalaureate Organization ............................................................................ 11
2.1.2 Sammanfattning.................................................................................................................... 12
2.2 Problemlösning............................................................................................................................ 12
3. Teori .................................................................................................................................................. 15
3.1 Behaviorism................................................................................................................................. 15
3.2 Kognitivsm .................................................................................................................................. 16
3.3 Konstruktivism ............................................................................................................................ 17
3.4 Sociokulturell teori ...................................................................................................................... 18
3.5 Analytiskt ramverk ...................................................................................................................... 19
4. Metod och genomförande .................................................................................................................. 21
4.1 Kvalitativ metod .......................................................................................................................... 21
4.1.1 Underlag för intervjuer ......................................................................................................... 21
4.1.2 Intervju som undersökningsmetod ....................................................................................... 22
4.1.3 Intervjuguiden ...................................................................................................................... 23
4.2 Urval och tillträde till fältet ......................................................................................................... 24
4.2.1 Skolor ................................................................................................................................... 24
4.2.2 Intervjudeltagare ................................................................................................................... 25
4.3 Validitet och reliabilitet ............................................................................................................... 25
4.4 Etiska överväganden.................................................................................................................... 26
5. Resultat – Presentation av intervjuer ................................................................................................. 27
5.1 Lärare: Anna ................................................................................................................................ 27
5.1.1 Synen på problemlösning ..................................................................................................... 27
5.1.2 Problemlösning i den egna undervisningen .......................................................................... 28
5.1.3 Läromedel, läroplan och problemlösning ............................................................................. 28
5.2 Lärare: Ben .................................................................................................................................. 29
6
5.2.1 Synen på problemlösning ..................................................................................................... 29
5.2.2 Problemlösning i den egna undervisningen .......................................................................... 30
5.2.3 Läromedel, läroplan och problemlösning ............................................................................. 30
5.3 Lärare: Clark................................................................................................................................ 31
5.3.1 Synen på problemlösning ..................................................................................................... 31
5.3.2 Problemlösning i den egna undervisningen .......................................................................... 32
5.3.3 Läromedel, läroplan och problemlösning ............................................................................. 33
5.4 Lärare: David............................................................................................................................... 33
5.4.1 Synen på problemlösning ..................................................................................................... 33
5.4.2 Problemlösning i den egna undervisningen .......................................................................... 34
5.4.3 Läromedel, läroplan och problemlösning ............................................................................. 35
6. Analys................................................................................................................................................ 36
6.1 Lgr 11 .......................................................................................................................................... 36
6.2 International Baccalaureate Organization ................................................................................... 37
6.3 Anna ............................................................................................................................................ 37
6.4 Ben .............................................................................................................................................. 38
6.5 Clark ............................................................................................................................................ 38
6.6 David ........................................................................................................................................... 39
6.7 Jämförelse.................................................................................................................................... 40
7. Diskussion ......................................................................................................................................... 42
8. Referenser.......................................................................................................................................... 44
Bilaga 1 ................................................................................................................................................. 46
7
1. Inledning
Under våra praktikperioder samt vid andra tillfällen då vi har haft kontakt med både
gymnasieskolor och grundskolor har vi märkt att lektioner, med visst undantag följer ett
mönster. Lektioner liknar den så kallade traditionella amerikanska undervisningen som enligt
Lester och Lambdin (2007) är lektioner där; läroboken är huvudkälla, uppgifter är utan
kontext (mekaniska uppgifter), läraren använder sig av en snabb genomgång med enkla
exempel samt att lärare och facit är de största auktoriteterna i klassrummet.
Matematikundervisningen är alltså fortfarande inspirerad av det som även brukar kallas
”katederundervisning”. Ändå så betonas vikten av att använda sig av problemlösning och
verklighetsbetonad undervisning tydligt i Lgr 11: ” Undervisningen ska bidra till att eleverna
utvecklar kunskaper för att kunna formulera och lösa problem samt reflektera över och
värdera valda strategier, metoder, modeller och resultat.” (Skolverket, 2011 s. 62). Att lärare
endast arbetar med en inledande genomgång följd av att elever arbetar i läroboken ger, enligt
vår uppfattning, inte förutsättningar för en utveckling i matematikens förmågor, som till
exempel problemlösning, resonemang, kommunikation och begrepp. Detta arbetssätt menar vi
istället innebär att eleverna lägger stor vikt i att träna procedurfärdigheten, eller vad man
skulle kunna kalla ett mekaniskt räknande.
I en undersökning av Helmertz (2010) jämfördes svensk och japansk undervisning. I
studien undersöktes skillnader och likheter när det gäller matematisk problemlösning. Detta
inspirerade oss att undersöka frågan vidare eftersom när vi haft kontakt med en internationell
skola i Sverige, upplevde vi att kunskaperna och engagemanget för problemlösning var större
där än i kommunala skolor. Detta gjorde att vi ville undersöka varför vi upplevde en sådan
stor skillnad mellan skolorna, med avseende på problemlösning. Eftersom vi själva har ett
intresse för arbete med problemlösning, kändes det naturligt att undersöka just detta område.
Utmaningen i undersökningen ligger i att det finns väldigt många faktorer som skiljer dessa
båda skolformer åt. Skolorna har olika läroplaner och olika läromedel. Dessutom ligger den
ena skolan i vad som skulle kunna betecknas som ett socioekonomiskt utsatt område, medan
den andra har en terminsavgift och därmed vänder sig till en annan socioekonomisk grupp.
Det finns undersökningar som har utgångspunkt i den socioekonomiska bakgrunden och
motivation i hur elever presterar i skolan. En sådan undersökning har till exempel gjorts av
Orlando Mella (2006) från Uppsala Universitet som heter ”Tre faktorer som tillsammans
förklarar skolresultat i Sverige: Socialklass, kön och etnicitet.” Studien baseras på sekundär
8
analys av data från PISA 2005 där Sverige bidrog till undersökningen med 4624, 15-åriga
elever, från 185 skolor. Kategorierna som undersöktes var matematik, läsförståelse och
vetenskap (NO-ämnen). Den socioekonomiska faktorn blev identifierad som viktig och som
något som tydligt påverkar skolresultaten. Till exempel utgör föräldrarnas utbildningsnivå den
faktor som har starkast påverkan på barnens skolresultat. ”Barn från medelklassen till exempel
har oftare tillgång till tidningar, datorer och internet i hemmet än barn i lågutbildade hem,
men framförallt delar de en miljö som förespråkar intellektuella aktiviteter och de
uppmuntras till att söka och tolka information.” (Mella, 2006 s. 9). För att avgränsa vårt
problem till matematiken så har vi endast valt att undersöka problemlösning och då lärarnas
syn på och arbetssätt med det mot bakgrund av att de arbetar i olika skolformer i Sverige.
1.1 Syfte
Syftet med arbetet är att undersöka och jämföra fyra lärares syn på problemlösning samt deras
berättelser i hur de arbetar med det, mot bakgrund av de två läroplaner som skolorna
använder.
1.2 Frågor

Hur ser lärarna på problemlösning?

På vilket sätt säger lärarna att de arbetar med problemlösning?

Påverkas lärarnas syn på och arbetssätt med problemlösning av den läroplan som finns
på skolan?
9
2. Bakgrund och tidigare forskning
I detta avsnitt kommer vi att presentera vad de olika läroplanerna och tidigare forskning
skriver om problemlösning. Ett syfte är att skapa en förberedelse inför intervjuerna medan ett
annat är att eventuellt kunna förstå lärarens syn på problemlösning i relation till den läroplan
som styr deras arbete. Vår undersökning kommer att ske genom intervjuer och då är det
nödvändigt att vara väl förberedda inför dessa för att kunna skapa en bra dialog.
2.1 Läroplanerna
Läroplanerna, Lgr11 och International Baccalaureate Organizations riktlinjer (IBO), som vi
beskriver i detta avsnitt kommer vi senare i arbetet att kort kommentera och analysera.
2.1.1 Lgr 11
Problemlösning är tydligt formulerad i Lgr 11 genom att vara presenterad som ett centralt
innehåll och som en förmåga samt att det tas upp i det syfte som matematikundervisningen i
skolan ska sträva efter. Problemlösning i syftet förklaras i att: ”Undervisningen ska bidra till
att eleverna utvecklar kunskaper för att kunna formulera och lösa problem samt reflektera
över och värdera valda strategier, metoder, modeller och resultat. Eleverna ska även ges
förutsättningar att utveckla kunskaper för att kunna tolka vardagliga och matematiska
situationer samt beskriva och formulera dessa med hjälp av matematikens uttrycksformer”
(Skolverket, 2011 s. 62). Läroplanen tar även upp användandet av digital teknik i att: ”Vidare
ska eleverna genom undervisningen ges möjligheter att utveckla kunskaper i att använda
digital teknik för att kunna undersöka problemställningar” (Skolverket, 2011 s. 62).
Problemlösning i det centrala innehållet för årskurs 7-9 tar upp:

Strategier för problemlösning i vardagliga situationer och inom olika ämnesområden
samt värdering av valda strategier och metoder.

Matematisk formulering av frågeställningar utifrån vardagliga situationer och olika
ämnesområden.

Enkla matematiska modeller och hur de kan användas i olika situationer.
(Skolverket, 2011 s. 67)
10
Problemlösning som förmåga förklaras med meningen: ”formulera och lösa problem med
hjälp av matematik samt värdera valda strategier och metoder” (Skolverket, 2011 s.63).
2.1.2 International Baccalaureate Organization
I International Baccalaureate Organizations riktlinjer (IBO) tas problemlösning upp på ett lite
annorlunda sätt än i Lgr 11. Begreppet kommer ofta upp och finns med i flera olika
matematiska områden. Tidigt i läroplanen står det att undervisningen ska sträva mot att:
arbeta med ”real-life problems” vars kontext passar eleverna. Det står vidare att man ska lära
ut olika strategier som medför olika lösningar och att elever ska kunna förklara lösningar och
reflektera över resultaten som fåtts. IBO tar även upp punkter som lärarna ska följa när de
planerar sina lektioner och även här är arbetet med problemlösning inkluderad i följande
mening: ”teachers should ensure that tasks allow students to think about the problem-solving
processes, reflect upon their methods and results, and explore the connection with everyday
life”(IBO, 2007 s. 16). Matematiken ska, enligt IBO, också utveckla tankefärdigheter,
”thinking skills”, där problemlösningsfärdigheten är en av dessa. Sedan beskriver IBO fyra
stora kriterier som matematikundervisningen ska sträva mot att utveckla hos eleverna.
Problemlösning i sig är inget kriterium, utan är något som ingår tydligt i tre av de fyra. De tre
kriterierna är:

”knowledge and understanding”: kunskap och förståelse är fundamentala för att
kunna skapa en grund i utvecklandet av problemlösningsfärdigheter. Kunskap och
förståelse utvecklar även resonemang som hjälper en att lösa problem.

”investigating patterns”, genom att undersöka mönster, får elever möjlighet att
använda sina matematiska kunskaper och problemlösningsfärdigheter för att skapa och
analysera information samt undersöka problem.

”reflection in mathematics”: eleverna ska kunna reflektera över sina
problemlösningsmetoder, samt kunna granska olika strategier, både egna och andras
vid arbete med problemlösning. (IBO, 2007)
Matematikundervisningen ska enligt IBO även utveckla ett tålamod och uthållighet vid
lösning av problem. Den ska skapa nyfikenhet för matematiken samt utveckla självsäkerhet i
11
användandet av matematik för att kunna analysera och lösa problem, både i skolan och i
verkliga situationer.
2.1.2 Sammanfattning
Båda läroplanerna tar upp problemlösning som en del av matematiken och skriver att det ska
läras ut. Läroplanerna kopplar även området till livet utanför skolan och redogör för en
anknytning till vardagliga problem. Medan Lgr 11 är mer tydlig i kategorisering av
problemlösning som ett centralt innehåll och förmåga är problemlösning beskriven i IBO mer
som en del av all matematikundervisning.
2.2 Problemlösning
Problemlösning ses som en viktig del av matematikundervisningen (Hagland, Hedrén &
Taflin, 2005). Matematikens primära mål är enligt Lgr11 att utveckla förmågorna
resonemang, kommunikation, begrepp och problemlösning vilket ska skapa en bättre
förståelse för matematiken. Områdena problemlösning och förståelse är relaterade till
varandra på så sätt att förståelse förbättrar problemlösningsförmågan och lärande genom
problemlösning utvecklar förståelse (Lester & Lambdin, 2007). Lärarens uppgift blir då att
kunna välja problem som passar eleverna och att kunna organisera lektioner så att de arbetar
med det som behövs. Det innebär att lämpliga uppgifter som uppfyller kraven för ett problem
och samtidigt anpassa samma problem till alla elever i en klass är en svårighet i sig. Alla
elever har förutsättningar för att lösa problem även om deras förmågor och baskunskaper
varierar, och alla elever har behov av att lyckas (Strandberg, 1991). Dåligt anpassade
uppgifter kan orsaka stora svårigheter inte bara hos elever med låg motivation, men även hos
de som är framgångsrika och intresserade av ämnet (Grevholm & Mouwitz, 2000). Enligt
Skoogh och Johansson (1991) så finns det vissa saker som en lärare inte ska göra under sin
undervisning i problemlösning: läraren ska inte ”förklara” för eleverna hur de ska lösa
problem, läraren ska inte ”programmera” eleverna att göra på ett visst sätt och läraren ska inte
”leda” eleverna mot svaret. Detta för att låta eleven själv utveckla en förståelse för olika
problem och sättet att lösa dessa. Då läraren har lyckats välja ut problem som fungerar bra i
sin elevgrupp och anpassat dem så att de passar alla eleverna är det dags att tänka på hur
eleverna ska arbeta. Enligt Hagland m.fl. (2005) har det arbetet tre delar/faser:
12
1. Introduktion av problem (läraren berättar, läser upp eller skriver på tavlan, använder
IT, ber en elev återberätta problemtexten)
2. Eleverna arbetar enskilt och/eller gruppviss med problem (lärare bestämmer gruppens
storlek, homogenitet eller heterogenitet)
3. Gemensam klassdiskussion kring elevernas lösningar och den matematik som då
aktualiserats
Vidare är det viktigt att klargöra elevens roll i undervisningen (Skoogh & Johansson, 1991).
Eleverna ska alltid försöka lösa problemen utan hjälp, anteckningar från försök ska sparas
samt att de ska försöka skriva så mycket som möjligt om själva problemet, där frågor såsom
vad vet jag? vad förstår jag? vad förstår jag inte? vad vill jag veta? osv. besvaras. Eleverna
ska även få använda sig av olika problemlösningsmetoder som till exempel återskapa
problemet praktiskt, rita bilder, söka mönster, arbeta baklänges, använda sig av tabeller, gissa
och kontrollera om svaret är logiskt samt testa att skriva om problemet med egna ord (Skoogh
& Johansson, 1991).
Vad är då ett problem? Hagland m.fl. (2005) förklarar att ett problem är en speciell typ av
uppgift som en person vill eller måste lösa. Den har inte en given procedur och ansträngning
behövs för att uppgiften ska kunnas klaras av. Vidare förklarar författarna att ett problem kan
klassas som rikt problem om den uppfyller vissa kriterier såsom:

introducera viktiga matematiska idéer eller vissa lösningsstrategier

informationen går att förstå

upplevas som en utmaning, kräva ansträngning och tillåtas ta tid

kunna lösas på flera olika sätt, med olika strategier och representationer

kunna initiera en matematisk diskussion utifrån elevernas skilda lösningar, en
diskussion som visar på olika strategier, representationer och matematiska
idéer

kunna fungera som brobyggare mellan olika matematiska områden

kunna leda till att elever och lärare formulerar nya intressanta problem
(Hagland m.fl., 2005).
För att förstå betydelsen av problemlösning i undervisningen har Jo Boaler (1998) jämfört två
skolor i England, där de sociala bakgrunderna var liknande, men där undervisningen i
matematik skilde sig åt. Ena skolan använde sig av ”katederundervisning” medan den andra
13
skolan arbetade mer med stora problemlösningsuppgifter och projektarbeten där eleverna
själva fick ta mycket ansvar. I skolan där det arbetades mycket med olika
problemlösningsprojekt visade att eleverna utvecklade en bra grundförståelse för
matematiken, utvecklade bra problemlösningsmetoder, ser en verklighetsförankring i
matematiken samt har mycket lättare att använda matematiken i vardagliga situationer än bara
i skolan.
14
3. Teori
Denna undersökning har en empiriskt grund och vår avsikt är att vara öppna för lärarnas svar i
intervjuerna. Därför gör vi ingen teoretisk positionering. Istället har vi, för att kunna förstå
våra lärares sätt att undervisa med problemlösning valt att ta till hjälp olika inlärningsteorier
som utgör grunden för det analytiska ramverk vi senare kommer att använda. På så sätt får vi
en viss överblick för hur teorierna är representerade utifrån det våra informanter berättar för
oss. Teorierna är grundade på frågor som berör vad lärande egentligen är och hur det går till
(Wyndhamn m.fl., 2000). De fyra teorierna är behaviorism, kognitivsm, konstruktivism och
den sociokulturella teorin. Sedan kommer vi genom ett analytiskt ramverk av Wyndhamn
m.fl. (2000) analysera intervjuerna som vi kommer att utföra med våra lärare.
3.1 Behaviorism
Idén med behaviorism är att det är möjligt att åstadkomma förändringar i en individs
beteende. Lärandet kommer in som en anpassning till något nytt eller ett uppsatt mål.
Behaviorismen var en dominerande teori i lärandepedagogiken fram till 1960-talet med
Burrhus Frederic Skinner som företrädare (Wyndhamn m.fl., 2000). Skinner (1969) menar att
med hjälp av yttre stimuleringar går det att förändra ett visst beteende. Ett önskvärt beteende
går att förstärkas genom att stimulera beteendet med till exempel belöning. Icke önskvärda
beteenden går det att reducera eller eliminera genom att försvaga stimulus, eller genom till
exempel bestraffningar. Genom att upprepa stimulus regelbundet resulterar det i att beteendets
förändring blir reflexartad. Den här metoden är känd som stimulus – respons och med det
menar Skinner att det är så inlärning sker (Skinner, 1969). Skinner tar upp tre teser som han
anser är viktiga vid inlärningsprocessen: lärande genom erfarenhet, lärande genom att vara
aktiv och lärande genom misstag. Läraren har en roll att överföra sina erfarenheter till sina
elever, som genom att vara aktiva och använda sig av erfarenheterna skapar nya kunskaper.
Sedan lär sig eleverna genom att den önskade kunskapen premieras, i vilket stimulus –
respons metoden kommer in (Skinner, 1969).
Belöning
Bestraffningar
Ökar chansen för att beteendet utförs igen
Minskar chansen för att beteendet utförs igen
(Figur 1)
15
Behaviorismen i matematiken är resultatfokuserad, där det rätta svaret samt berömmande
respons från läraren ger eleven en vilja att räkna vidare (Wyndhamn m.fl., 2000).
Den allmänna bilden i behaviorismen för hur klassrummet ska vara är:

Kunskapen är given

Passivt lärande med mycket upprepningar

Eleven som passiv mottagare

Läraren är auktoritativ, anvisande och övervakande (Wyndhamn m.fl., 2000).
3.2 Kognitivsm
Kognitivismen, till skillnad från behaviorismen, är mer intresserad i hur individen hanterar
information som ges (Wyndhamn m.fl., 2000). Jean Piaget utvecklade teorin då han förutom
att titta på beteende även la vikt på inlärningen som en individuell kognitiv process. Han
ansåg att utvecklingen skedde med hjälp av både yttre faktorer, såsom miljö samt inre
faktorer, såsom erfarenheter. Piaget ansåg också att inlärningen styrdes av de erfarenheter
som fanns i individen (Piaget, 1968). I matematiken kan då individens kognitiva förmågor och
mentala tankeprocesser ses som viktiga i att till exempel förstå problemlösning. Kunskap ses
dock som något givet i teorin. Inom kognitivismen finns det olika förgreningar som till
exempel HIP-teorin (Human Information Processing) som på svenska kan översättas till
informationsbehandling (Wyndhamn m.fl., 2000). Sättet att se på inlärning genom HIP hjälper
att konstruera modeller på hur tänkandet sker vid till exempel i arbete med problemlösning.
Kort kan det beskrivas med hjälp av följande bild
Problem
Uppgift
Omgivning
(Miljö)
Uppgift
(Figur 2)
Sensorisk
input
Långtidsminne
Matematiska kunskaper
Metakunskaper
Omvärldskunskaper
Arbetsminne
Självreglerande processer
Mentala representationer
(Wyndhamn m.fl., 2000, s. 87)
16
Output
Bilden berättar att en uppfattar ett problem på ett visst sätt och sedan genom samarbete mellan
arbetsminne och långtidsminne får fram en lösning. Med hjälp av informationsbehandlings
teorierna går det då att beskriva beteende som målinriktade handlingar (Wyndhamn m.fl.,
2000). En lektion i den kognitiva teorin kan innehålla:

Lärare som intar roll som ordförande i diskussioner men aldrig som bedömare

Eleven ska själv hitta strategier för att uppnå resultat

Elever ska även värdera lösningar och reflektera över det de gjort
(Wyndhamn m.fl., 2000)
3.3 Konstruktivism
Konstruktivismen kan ses som en del av kognitivismen då båda teorierna lägger stor vikt på
det kognitiva och erfarenheter men där konstruktivismen förklarar kunskap som något som
individen konstruerar utifrån sina egna erfarenheter (Wyndhamn m.fl., 2000; von Glasersfeld,
1990). Det är samspelet mellan sinnesintryck och förnuft som konstruerar kunskapen.
Processen kan förklaras genom att individen gör en handling med hjälp av sina erfarenheter,
reflekterar över det som har skett vilket sedan resulterar i ny kunskap och lärande. Ernst von
Glasersfeld, som utvecklade termen radikal konstruktivism (individuell konstruktivism)
beskriver inlärning med:”Knowledge is no passively recieved either through the senses or by
way of communication. Knowledge is actively built up by the cognizing subject.”(von
Glasersfeld, 1990, s. 22-23). Han menade att kunskap och förståelse är något individuellt och
är beroende av tidigare erfarenheter. Erfarenheterna som fås är subjektiva och påverkar då hur
vi uppfattar nya intryck och inlärning. På så sätt är kunskap enligt konstruktivismen också
relativ, det är något som varierar med tiden och miljön (von Glasersfeld, 1990). Detta
överensstämmer med Piaget som menade att det sker förändringar i individens kognitiva
strukturer vid tolkning av händelser och information som sedan görs begripliga. Han delar
upp inhämtningen av kunskap till två begrepp: assimilation och ackommodation. Assimilation
betyder att individen kan tolka nya händelser med hjälp av tidigare erfarenheter medan
ackommodation betyder att erfarenheterna måste omkonstrueras för att förstå och lösa den
nya händelsen (Piaget, 1968).
I den konstruktivistiska teorin kan lektioner innehålla:
17

Diagnoser för att rätta till fel och missuppfattningar

Begrepp representeras på olika sätt

Förklara skillnader mellan matematiken i skolan och matematiken utanför skolan

Tydlighet vilka mål som eleverna ska kunna klara av
(Wyndhamn m.fl., 2000)
3.4 Sociokulturell teori
Lev Vygotskijs sociokulturella teori utgår ifrån att individens beteende och tankeprocesser
inte kan utvärderas endast utifrån det kognitiva. Hänsyn måste också tas till den kultur som
finns i samhället. Individen föds och utvecklas alltså i den rådande samhällskulturen
(Vygotskij, 1978). Vygotskij förklarar också att miljö och språk har en central roll i
inlärningsprocesserna, där han gör en skillnad mellan ”sign” (tecken, språk, symboler) och
”tools” (hjälpmedel, artefakter). Båda begreppen har en likhet i att de används för att förmedla
kunskap (Vygotskij, 1978). Han menade också att samspelet med omgivningen är avgörande
för individens utveckling och lärande: ”… what children can do with the assistance of others
might be in some sense even more indicative of their mental development than what they can
do alone.” (Vygotskij, 1978, s. 85) Teorin beskriver även att sättet vi tänker på och uppfattar
information om världen är färgad av den kultur som är dominerande (Wyndhamn m.fl., 2000).
Vygotskij anser för att kunna optimera kunskapsutvecklingen är det viktigt att hitta en
individs ”zone of proximal development”. Han förklarar det som vad som kan uppnås
kunskapsmässigt med stöd av andra i omgivningen: ”It is the distance between the actual
developmental level as determined by independent problem solving and the level of potential
development as determined through problem solving under adult guidance or in collaboration
with more capable peers.”(Vygotskij, 1978, s. 86). Vygotskij förklarar också att det finns en
aktuell utvecklingsnivå, vilket han beskriver som hur mycket individen kan i en given
tidpunkt, men anser att det inte räcker för att förstå kunskapsutvecklingen och därför måste
det tas hänsyn till vad individen kan uppnå med hjälp av omgivningen (Vygotskij, 1978).
Vidare går det att säga att individen agerar utifrån sina egna kunskaper och erfarenheter,
samt av vad omgivningens normer tillåter i en viss situation. Undervisning som följer den
sociokulturella teorin betonar:
18

Lärande som en social och samarbetsbetonad aktivitet

Problemlösning med anknytning till vardagliga situationer

Ta hänsyn till elevernas erfarenheter utanför skolan

Verbal förmedling från läraren
Läraren ska agera organisatör, deltagare, utvärderare samt vara stöd till eleverna under
undervisningen (Wyndhamn m.fl., 2000).
3.5 Analytiskt ramverk
Vi kommer använda oss av ett analytiskt ramverk baserad av Wyndhamn m.fl. (2000) som
bygger på de fyra lärandeteorier, som vi har presenterat ovan, behaviorism, kognitivsm,
konstruktivism och sociokulturell teori. Modellen har två tydliga dimensioner, där den ena
berör relationen mellan inlärning och tillämpning medan den andra dimensionen berör
relationen mellan arbetsätt och tankeprocess. Ramverket använder vi som stöd för att
undersöka hur problemlösning uppfattas och används hos våra lärare. Den kommer även att
användas vid en översiktlig reflektion av de två läroplanen som skolformerna följer. I
relationen mellan inlärning och tillämpning kan problemlösning ses som antingen ett sätt att
lära sig något nytt eller som något där tidigare kunskaper kan tillämpas. I den andra
dimensionen syftar arbetssätt på hur problemlösning rent praktiskt utförs medan tankeprocess
syftar på olika kognitiva processer vid själva arbetet.
TILLÄMPNING
ARBETSSÄTT
(Figur 3)
B
A
C
D
TANKEPROCESS
INLÄRNING
I modellen skapas det fyra fält som har olika egenskaper. Fält A handlar om hur olika
strategier, tekniker eller regler tillämpas vid problemlösning. Dessa egenskaper är starkt
19
anknutna till kognitivismen. I fält B är det praktiska arbetet viktigt, samt att problemlösning
sker för att kunna tillämpa tidigare kunskaper och här är det resultatet som står i fokus. Fält B
kan då knytas till behaviorismen. Fält C tar upp egenskaper där elever arbetar i grupper,
diskuterar, använder konkret material samt genom arbetet med problemlösning lära sig något
nytt. Fältets egenskaper passar bra med den sociokulturella teorin. I det sista fältet, fält D,
läggs intresse mycket på att elever ska reflektera över sina lösningsmetoder och erfarenheter
som fås under själva arbetet. Mycket fokus läggs på att tänkandet ska utvidga kunskaperna.
Fält D ses som ett område passande till konstruktivismen.
20
4. Metod och genomförande
I detta avsnitt kommer vi att redogöra för våra metodologiska ställningstaganden, som varför
vi har valt en kvalitativ metod. Vidare kommer vi att beskriva intervju som metod, med dess
fördelar och begränsningar. Vi berättar också hur vi fick tillträde till fältet och vilka etiska
ställningstaganden vi har gjort, samt studiens validitet och reliabilitet.
4.1 Kvalitativ metod
I vår undersökning kommer vi använda oss av en kvalitativ metod. Kvalitativa metoder, till
skillnad från kvantitativa, är inte fokuserade på att få fram kvantifierad resultat (Hur mycket?
Hur många?). Istället är det viktiga att få en förståelse för hur de människor som undersöks
upplever de frågor som ställs (Hartman, 2004), i vårt fall lärares syn på och arbete med
problemlösning. Ett sätt att genomföra en kvalitativ undersökning är genom intervju vilket vi
har valt att använda.
4.1.1 Underlag för intervjuer
Intervjuerna kommer genomföras halvstrukturerat (Hartman, 2004). Det betyder att det finns
frågor som är förberedda som stöd för att leda intervjun, men där det lämnas utrymme för en
öppnare diskussion kring ämnet. Möjlighet fanns att om det dyker upp frågor i samtalet med
den första deltagaren, att dessa frågor även används hos de andra. Just denna egenskap hos
halvstrukturerade intervjuer som sker med flera deltagare ökar våra möjligheter för att uppnå
resultat. Till skillnad från enkätundersökning som metod är fördelen med en intervju att
intervjuaren kan förklara vissa frågor som kan upplevas som oklara. Därmed förhindras att
intervjudeltagaren automatisk anger ett svar, vilket som helst, bara för att svara på frågan.
Konsekvensen av detta är att svaren har större trovärdighet i en muntlig intervju (Bryman,
2011). Nackdelarna med intervju som metod är att den kräver personlig kontakt mellan
frågeställaren och intervjudeltagaren och att de muntliga frågorna och svaren är väldigt
tidskrävande. Likaså kan den som intervjuar påverka svaren i större utsträckning.
Intervjuarens viktigaste egenskaper är att han eller hon är väl förberedd inför intervjun och att
de kan skapa en bra miljö där den intervjuade ska känna sig avslappnad och bekväm i att
svara på ställda frågor (Hartman, 2004)
21
Intervjun som en analytisk induktionsmetod utmärks dels av en frihet hos frågeställaren att
välja frågor som inte är standardiserade eller stängda vilket i sin tur resulterar i att
frågeställaren kan improvisera utifrån den intervjuades svar, vilket gör metoden väldigt
flexibel (Hartman, 2004). I en sådan intervju är miljön avslappnad och det faktum att den
intervjuade kan uttala sig fritt utan formella, innehållsmässiga begränsningar resulterar i svar
som är innehållsrika, detaljerade och baserade på egna erfarenheter. Intervjuerna kommer att
spelas in med hjälp av en diktafon. Fördelarna med inspelad intervju är att frågeställaren inte
behöver tappa fokus genom att anteckna svaren direkt utan kan lyssna på det inspelade
materialet vid senare tillfälle och då upptäcka saker som vid samtalet hade missats eller
uppfattats på ett annat sätt (Bryman, 2011).
De problem som man kan råka ut för i en halvstrukturerad intervju handlar återigen om tid
och resurser eftersom alla intervjuer av sådan art är tidskrävande. Ett annat problem är att
frågeställaren på grund av den frihet den ostrukturerade intervjun har, kan påverka och rikta
den intervjuades svar (Hartman, 2004). För att undvika en sådan situation kommer vi att
sträva efter att våra frågor är icke-suggestiva, så kallande icke-ledande frågor.
För att underlätta uppgiften, skapa trygghet och förtroende så har intervjudeltagarna innan
intervjuerna fått information om de områden som intervjuerna kommer gå in på. En av
intervjuerna kommer att ske på engelska, vilket innebär att temaområden och själva frågorna
samt transkribering av den färdiga intervjun kommer att översättas. Intervjuerna kommer att
ske där enligt Bryman (2011) deltagarna känner sig mest bekväma, alltså i deras skolmiljö
(kontor).
4.1.2 Intervju som undersökningsmetod
Intervju som metod är ”en lämplig metod för att skaffa fram autentisk eller äkta kunskap och
intervjuarens roll är att avslöja den sanna identitet som befinner sig under ytan” (Ryen, 2004
s.12). Hartman (2004) urskiljer två grenar inom den kvalitativa undersökningsmetoden:
analytisk induktion och interaktiv induktion. Den analytiska induktionen eller den
traditionella metoden betyder att man först samlar data från en informant och senare
analyserar det. Inom interaktiv induktion sker istället datainsamling och dataanalys
omväxlande. I det här arbetet kommer vi att låta oss inspireras av analytisk induktion. Den
analytiska induktionen är fördelad i tre etapper: planering, datainsamling och dataanalys
(Hartman, 2004).
22
1. Planeringsfasen. Planeringsfasen har två viktiga moment: det första är att man
formulerar en fråga som man vill att undersökningen ska ge svar på och det andra
momentet är valet av kunskapskällor.
2. Datainsamling. De kvalitativa studierna är mycket friare än de kvantitativa studierna
när det gäller källor och i denna fas krävs känslighet för vad som är viktig
datainsamling och vad som är intressant för frågeställningen.
3. Analys av kvalitativ data. Här analyserar man det insamlade datamaterialet så att en
teori växer fram. I vårt fall kommer vi även att använda oss av det analytiska ramverk
som presenterats tidigare.
(Hartman, 2004)
Knut Kjeldstadli (2009) skriver att tolkningsprocessen betecknas ibland som en
”hermeneutisk cirkel”. Det betyder att en tolkning växer fram i en cirkulär rörelse mellan
individens förförståelse och möten med nya antaganden, kategorier och fenomen, vilket leder
till ny förståelse som i sin tur blir förförståelse i kommande tolkningsansatser. Kjeldstadli
beskriver hela denna process med följande ord:
”Lite tillspetsat kan man säga att det är först när undersökningen är genomförd som man vet vad man
har gjort. Att skriva inledningen i slutet är det naturlig svar på processen, inte något man bör
skämmas för och sopa undan”. (Kjeldstadli, 2009, s.130)
I vår studie avspeglar sig detta i att vi vill vara öppna för våra informanters berättelser, vilket i
sig innebär att de kunde ändra våra uppfattningar genom sina berättelser. Att vänta tills
informationen är samlad och behandlad kan då ge oss en helt ny bild vilket kan resultera i att
vi ändrar syfte och frågeställning något.
4.1.3 Intervjuguiden
Enligt Hartman (2004) är det viktigt att intervjuaren är ordentligt förberedd för att kunna hålla
samtalet till det område som är av intresse (se bilaga 1). Samtidigt har vi velat vara öppna för
informanternas egna berättelser. För att uppnå detta förbereds det en intervjuguide före själva
intervjuerna för att minska risken att lämna intervjun med irrelevant material. I intervjuguiden
tar man upp teman som ska diskuteras och utför dem i en viss ordning. Våra temaområden till
intervjuerna är:
23
1. Synen på problemlösning/ The view on problem solving
2. Problemlösning i den egna undervisningen/ Using problem solving in their own
teaching
3. Läromedel, läroplan och problemlösning/ Teaching materials, curriculum and
problem solving
4.2 Urval och tillträde till fältet
De skolor som lärarna arbetar på är då en internationell och en kommunal. Lärarna är sedan
tidigare bekanta för oss, vilket underlättade tillträde till skolorna.
4.2.1 Skolor
Den internationella skolan är centralt placerad i en stad i Sverige. Skolan har både Primary
Years Programme (Lågstadium) och Middle Years Programme (Högstadium). Den är vad
som i en svensk skola skulle kallas en F-9 skola. Antalet elever uppgår till mer än 300
stycken, från 30 olika länder. All undervisning i skolan sker på engelska. Undervisningen i
matematik genomförs i den här skolan med homogena grupper. Med det avses att eleverna är
grupperade kunskapsmässig i matematikundervisningen. Eleverna har matematik fyra gånger
i veckan, där varje lektion är 60 minuter långa. Klasserna är vanligtvis i en storlek med cirka
20 elever där fördelningen mellan pojkar och flickor är jämn. För att ges möjlighet att gå på
skolan finns det kriterier som måste uppnås samt att utbildningen är avgiftsbelagd:
1. Engelska som modermål eller som andraspråk, där boendet i Sverige är tillfällig.
2. Icke engelsk-talande elever, där boendet i Sverige också är tillfälligt.
3. Icke engelsk-talande elever som är bosatta i Sverige men planerar flytta utomlands.
4. En engelsk-talande förälder där familjen flyttar utomlands.
Den kommunala skolan ligger i utkanten i samma stad som den internationella. Skolan är en
F-9 skola med cirka 450 elever. Majoriteten av eleverna har utländsk bakgrund och många av
dem är nyanlända där språkförbistringen anses vara ett problem för skolan. Skolan kallar sig
en modern multikulturell grundskola, enligt deras hemsida. I den här skolan, till skillnad från
den internationella, sker undervisningen med heterogena klassgrupperingar. Det är även så att
matematiklektionerna är uppsatta på en och samma dag och det innebär att eleverna har
24
matematik tre timmar i rad. Antalet elever per klass är cirka 20 stycken och
genusfördelningen är även här jämn.
4.2.2 Intervjudeltagare
Intervjudeltagarna har valts genom en purposive sampling, vilket betyder att de valdes för att
passa vår undersökning (Bryman, 2011). De som har valts är högstadielärare i matematik på
de utvalda skolorna samt med varierande erfarenheter och bakgrund. Själva urvalet av
intervjupersoner var begränsad till antal eftersom det inte finns så många matematiklärare på
varje skola. Problemet med ett så litet urval är att det finns en risk att lärare inte ställer upp
vid intervjuer, men vi hade tur att ett sådant problem inte uppstod. Alla på de båda skolorna
hade möjlighet att delta i vår undersökning vilket gav oss alternativ att välja. Vårt syfte är att
titta på dessa lärares syn på problemlösning, samt arbetssätt mot bakgrund av sina egna
erfarenheter och skolan de arbetar på. Därför valde vi lärare med olika erfarenheter.
Lärarna har vi valt att namnge till Anna, Ben, Clark och David. Lärarna Anna och Ben
arbetar på den internationella skolan medan Clark och David arbetar på den kommunala.
Anna är en lärare med utbildning och bakgrund från U.S.A medan Ben har sin bakgrund från
f.d. Jugoslavien och med en lärarutbildning i Sverige. Clark och David har båda sin utbildning
i Sverige där Clark även har sin uppväxt i medan David har sitt ursprung i södra Europa.
Arbetserfarenheten varierar från några år till några decennier.
4.3 Validitet och reliabilitet
Validitet (giltighet) och reliabilitet (trovärdighet) är viktiga begrepp inom vetenskaplig
forskning. Inom kvalitativ undersökning går det att dela upp reliabilitet och validitet i fyra
undergrupper: Intern och extern reliabilitet samt intern och extern validitet (Bryman, 2011).
Hög intern reliabilitet innebär att gruppen som intervjuar och analyserar data gör det med en
färdig strategi i hur informationen som ges uppfattas, medan extern reliabilitet avser hur väl
intervjuerna och textanalyserna kan replikeras. Hög intern validitet visar hur väl
observationer/intervjuer stämmer överens med de teoretiska idéer som finns medan extern
validitet istället rör i vilket mån resultaten som fås kan generaliseras till andra sociala miljöer
och situationer (Bryman, 2011). I vår studie kan den interna reliabilitet och den interna
validiteten anses hög. Den interna reliabiliteten är hög på grund av att vi båda från början haft
25
en klar strategi av vad vi vill uppnå, samt att analysen kommer ske med ett klar analytisk
ramverk. Den interna validiteten kan också anses hög då undersökningens roll är att få fram
lärares syn på problemlösning och deras sätt att arbeta med det, och genom att intervjua dessa
lärare med frågor som omfattar vårt intresseområde får vi svar på det som behövs i
undersökningen. Däremot kan den externa reliabiliteten ses som låg då intervjuerna har skett
halvstrukturerade samt att den personliga kontakten kan påverka hur lärarna svarar på våra
frågor. Även den externa validiteten i studien kan anses som låg då våra resultat endast gäller
för de lärare vi intervjuat och kan inte generaliserar för landets lärare eller skolor.
4.4 Etiska överväganden
Alla lärare har fått tydlig information om att deltagande är frivilligt samt anonymt. Resultaten
av intervjuerna kommer att behandlas konfidentiellt och deras svar kommer endast att
användas i denna undersökning (Vetenskapsrådet, 2011). Samtliga lärare har givit tillstånd att
intervjuerna får spelas in via en diktafon för att kunna analyseras vid ett senare tillfälle. Vi har
också varit noga med att inte ställa frågor av privat natur, eller som kan skada, eller upplevas
som otrevliga (Bryman, 2011). För att försäkra lärarna anonymitet så är deras namn fingerade.
26
5. Resultat – Presentation av intervjuer
I detta avsnitt presenterar vi kort våra informanters bakgrunder och berättelser för att kunna
ge en tydlig bild av det de har sagt. Informanternas intervjuer kommer att presenteras var för
sig och kommer att följa de områden som togs upp i intervjuguiden. Vi intresserar oss för
olika uppfattningar som av olika anledningar finns i allas våra medvetanden, men vi vill också
presentera de människor som hjälpt oss att få fördjupad förståelse för dessa uppfattningar.
5.1 Lärare: Anna
”If you are doing problem solving, I think it has to be when kids can, when it’s more open ended”
Anna är uppväxt och utbildad i USA. Under sin tid som lärare har hon upplevt ”drill and kill”
metoden, men har märkt att mycket har förändrats sen hon började arbeta som lärare, både
positivt och negativt. Hon har arbetat i mer än två decennier i en privat skola i Nord Amerika
och sedan början av 2000-talet arbetar hon på en internationell skola i Sverige.
5.1.1 Synen på problemlösning
Anna anser att problemlösning är viktig eftersom det är något som används i arbetslivet.
Enligt henne hjälper det utvecklingen av matematiken att samarbeta med andra och att samt
kunna hitta logiska lösningar. För henne innebär problemlösning att hitta förslag till lösningar,
prova lösningsförslagen och sen försöka få dem att fungera. Hon tycker att ett bra problem är
ett problem där man kan komma till olika resultat, hitta olika vägar att uppnå resultaten och
där eleverna kan förklara sina lösningar. Anna säger också att även om eleverna kan lära sig
att räkna mekaniskt, så är den kunskapen onödig om de inte kan använda den i andra
situationer. Så att bara lära elever ”mechanical mathematics”, eller som man i U.S.A säger
”drill and kill”, är oanvändbart. Anna säger att lärarens uppgift är att lära elever tänka
matematiskt och inte att bara räkna.
27
5.1.2 Problemlösning i den egna undervisningen
Anna berättar att under hennes lektioner används problemlösning ofta. Hon anser att det är
viktigt att eleverna får diskutera och reflektera i matematiken. Hon låter alltid sina elever
diskutera problemen, tillvägagångssätten och resultaten. Men hon säger också att, hur mycket
eleverna arbetar med problemlösning beror på matematikområdet och elevernas motivation.
Dock så har hon alltid med diskussion och reflektion i sina lektioner. Hon berättar också att i
diskussionerna sker det att eleverna diskuterar vardagssituationer där matematiken de lärt sig
används, för att försöka få en mer vardagsanknytning. Hon berättar också att när eleverna
arbetar med problem, brukar de oftast börja arbeta individuellt för att sedan i grupper, till
exempel om fyra, diskutera problem och lösningar. Anna berättar för oss att klasserna i
matematikundervisningen är nivågrupperade och det medför att planeringen och utförandet av
lektionerna skiljer sig lite åt. Hon berättar vidare att utförandet är något som startats den här
terminen och det positiva, enligt henne, är att det blir lättare att skapa lektioner och att
eleverna får arbeta med det de behöver.
Anna berättar att hennes lektioner inte är ”textbook driven”, utan att hon själv väljer vilka
typer av uppgifter och problem som behövs till lektionerna, till exempel med hjälp av olika
typer av matematikböcker och lärarhandledningar. Hon säger också att matematikboken, som
eleverna får som CD, är ett komplement och skulle det behövas mer arbete i ett visst område,
är uppgifterna lättillgängliga för eleverna.
Eftersom eleverna har datorer skapar det möjligheter för dem att arbeta med
problemlösning på annat sätt, enligt Anna. Hon berättar att skolan använder ett speciellt
program, mathletics.eu, där lärare kan skapa uppgifter som eleverna sedan får lösa. Även
Internet i allmänhet används hos eleverna för att söka information.
5.1.3 Läromedel, läroplan och problemlösning
Anna anser att det står tydligt i IBO om arbetet med problemlösning, att elever måste kunna
samarbeta med andra, reflektera samt diskutera matematik. Hon anser att läraren har en frihet
att lära ut det som står i läroplanen, med tydliga krav vad eleverna ska uppnå i kunskapsnivå
när de går ut MYP (Middle Year Program). När det gäller läromedlen, berättar Anna att det
inte är något som följs hela tiden utan det är hennes personliga undervisningserfarenheter som
följs.
28
5.2 Lärare: Ben
”Jag förespråkar spontanitet. Planering i all ära, men som lärare måste det finnas ganska stora
marginaler för improvisation, spontanitet, att man avviker från planeringen och den vägen som man
hade tänkt innan lektionen satte igång.”
Ben är född i Sverige och har även gått grundskolan i Sverige. I början av 80-talet avslutade
Ben grundskolan och flyttade till hemlandet (F.d. Jugoslavien) där han påbörjade och
avslutade gymnasieutbildningen. Han tog med sig sina erfarenheter från den svenska skolan
till f.d. Jugoslavien och blev där ”chockad” av undervisningen och de pedagogiska
metoderna. Under sin tid i grundskolan i Sverige minns Ben att det var mer krävande
kunskapsmässigt, striktare disciplin och läraren hade större auktoritet än idag. I skolan i f.d.
Jugoslavien var situationen ännu mer krävande och strikt. Ben minns inte hur lärarna på
grundskolan arbetade med problemlösning, men ser en likhet mellan kraven då och i den
internationella grundskolan idag. Lärarutbildningen har Ben från Sverige. Läraren har arbetat
sedan några år tillbaka som matematik och NO-lärare. Han har arbetat i kommunal skola i
fåtal år och på senaste tiden har Ben arbetat i internationell skola, men endast med matematik.
5.2.1 Synen på problemlösning
Ben berättar att begreppet problemlösning är för honom en bred definitionsfråga. Men
matematiskt problem ser han som något som har olika vägar för att uppnå resultat, där olika
typer av hjälpmedel (till exempel miniräknare, böcker och dator) kan vara tillhjälp. Ett
problem ska även, enligt honom, kunna anpassas till alla elever så att de kan förstå, lösa,
”snappa upp” mönster, förstå mönster och kunna generalisera. I problemet ska det även vara
tydligt vad som är givet och vad som inte är givet, så att eleverna vet vilken väg de ska ta.
Ben tar sedan upp begreppet Problem Based Learning, PBL, som ett sätt att lösa problem.
Metoden, berättar han, kan användas i matematikundervisningen, men är även användbar i
andra ämnen och situationer. Ben anser också att arbetet med problemlösning är givande för
eleverna då dessa elever, förutom utveckling i matematik, även är ett sätt att förberedda dem
för det praktiska i livet.
29
5.2.2 Problemlösning i den egna undervisningen
Ben berättar att när han planerar undervisningen så utgår han inte ifrån problemlösning som
central innehåll, utan att det är något som kommer naturligt under själva lektionerna.
Problemen som kommer fram under tiden skapas med hjälp av Bens erfarenheter och tar
hänsyn till elevernas kunskapsnivåer. Ben betonar att han förespråkar spontanitet i sin
undervisning där läraren ska ha stora marginaler för improvisation, samt att en lärare ska klara
av att avvika från den planerade undervisningen. Men det ska alltid finnas en ”röd tråd” som
ska följas. Ben säger vidare att något som är viktigt för eleverna är att läraren ”pushar” dem,
för att få dem att utvecklas. Detta gör han till exempel genom att använda sig av uppgifter och
problem som ligger några nivåer högre i form av en utmaning, vilket skapar en nyfikenhet hos
eleverna. Det är enligt honom lättare att fånga elever när problemen är lite svårare än vad de
är vana vid, att de går in på ”okänd mark”. Han säger också att bara arbeta med
uträkningsuppgifter gör att eleverna tröttnar och tappar fokus, medan nya begrepp och nya
moment skapar nyfikenhet. Men å andra sidan, menar han, är det inte hållbart med att endast
arbeta med svårare problem och med nya moment, då det inte skapas kontinuitet hos eleverna.
Det som kan ske är att läraren och eleverna missar att arbeta med ett område som kursplanen
kräver. Problemlösning är något alla eleverna arbetar med, ”ibland i grupp, ibland
individuellt”, beroende på uppgiftens struktur, omfattning och själva det matematiska
området. Ben berättar att han bara ibland arbetar med laborativa övningar på grund av
tidsbrist. Däremot när det gäller IT-teknik så är Ben positiv. Till sin hjälp använder han till
exempel Internet, där eleverna kan söka information om begrepp, historia och om
matematiska moment och problem. Ben och eleverna på den internationella skolan har även
tillgång till ett program där Ben kan ge sina elever läxor och uppgifter efter deras behov. Via
programmet kan Ben se statistik på hur många som har gjort uppgifterna, samt resultat.
Programmet ger även eleverna chans till att tävla, både mot varandra och internationellt. På så
sätt skapas då en utmaning hos eleverna att vilja lyckas enligt Ben. Det finns även ett
rankingsystem i programmet som visar vilka resultat eleverna uppnår. Tävlingsmomenten
används oftast som en ”morot” för eleverna och uppgifterna i momenten är oftast av enkel
karaktär.
5.2.3 Läromedel, läroplan och problemlösning
I läroplanen, IBO, förklarar Ben att det står att varje elev ska få den hjälp den behöver och att
alla elever ska synas. Varje elev ska få chansen att utvecklas kunskapsmässigt och även som
30
individ. Problemlösning är en del av detta. Fördelarna med IBO, ser han vara att den har
ganska tydliga hänvisningar när det gäller matematikinnehållet, samt ger bra information i
bedömning av eleverna. När det gäller användandet av läromedel, där Ben inkluderar till
exempel miniräknare, IT-program och matematikböcker, har han inga krav från ledning eller
läroplan på hur dessa ska användas, utan det är Ben som avgör vad som behövs.
Matematikböcker är inget som följs ”slaviskt”, utan böckerna är mer som ett riktmärke vid
undervisningen. Böcker anses även vara något som skapar en trygghet hos eleverna, då
eleverna har enklare att följa riktningen i undervisningen.
5.3 Lärare: Clark
”Det tror jag för många elever är någonting som de får med sig i framtiden… ju fler problem de
arbetar med, desto olika problem, desto mer erfarna blir de. Jag tror det är positivt.”
Clark avslutade sin grundskoleutbildning i mitten av 70-talet i Sverige. Han upplevde sin
utbildningstid i grundskolan som betydligt mer krävande än dagens skola. Kunskapskraven
upplevde han som betydligt högre, samt så var lärarens roll mer auktoritativ. När det gäller
problemlösning, så minns Clark att det fanns men att det var väl inbäddat i
matematikundervisning. Lärarutbildningen gjordes och avslutades i Sverige, och under
2000-talet har Clark arbetat som matematik och NO-lärare i några grundskolor.
5.3.1 Synen på problemlösning
På frågan: Vad är problemlösning för dig? svarade Clark att det är något som är viktigt för
eleverna att arbeta med, då det är något de får med sig i framtiden. Enligt Clark skapar
eleverna en erfarenhet som för dem är positiv. De lär sig att lösa problem med hjälp av
matematiken och får kunskaper att använda olika typer av förbestämda strategier. Därför är
problemlösning, enligt Clark, givande: ”Vi ska utveckla deras förmåga, deras
problemlösningsförmåga.” Ett matematiskt problem, är för Clark ett problem som går att lösa
på olika sätt. Sen säger han att ett problem för en elev behöver inte alltid betyda att det är ett
problem för en annan.
31
5.3.2 Problemlösning i den egna undervisningen
Clark anser att läraren ska ta initiativ för att presentera problem, så att eleverna får en
förståelse för problemet: ”låt eleverna ställa frågor...”. Clark förklarar att det finns elever
med svårigheter att uppfatta texter och själva problemet. Dessa elever måste då få en ”chans”
att diskutera och att ställa frågor för att ge sig in i det: ”De måste äga problemet.”. Clark
betonar viktigheten att eleverna måste förstå problemet för att kunna lösa det.
Hur ser en problemlösningslektion ut hos Clark? Clark berättar att han har olika problem
nedskrivna på papper, som han antingen presenterar vid tavlan eller delar ut problemet till
eleverna. Efter presentation får eleverna ställa frågor om det är något de inte förstår. Han
menade att i hans skola ställs de flesta frågorna angående textförståelsen och mindre om det
själva matematiska innehållet: ”Det kan till exempel vara vilket av någonting, om de säger
vilket då är det bara ett, säger man vilken eller vilka, det kan innefatta fler.” Clark berättar
vidare att eleverna i början arbetar med ett problem själva, för att sedan i par eller grupper om
tre, diskutera lösningsmetoder och fortsätter att försöka lösa problemet. Detta gör, enligt
Clark, att eleverna förstår och ”äger” problemet. För Clark är det ideala gruppfördelningen
mellan två och tre elever, medan större grupper kan betyda större störningsmoment. I sådana
grupper, menar Clark, att svagare elever ”glider undan”. De lär sig inte. Om det uppkommer
svårigheter vid problemlösning avböjer Clark, direkt inbladning i form av hjälp. Eleverna får
gärna fråga andra elever om hjälp för att på så sätt öka diskussionen inom matematiken. Han
betonar också att elevernas personliga relation kan bidra till lyckad problemlösning: ”De är
lite svaga, men de två tillsammans fixar det rätt bra.” (Pratar om två elever). Clark säger
vidare att om en elev, eller grupp i klassen har löst ett problem på ett bra sätt, kan han göra att
eleven/gruppen redovisar sin lösning framför hela klassen.
Den kommunala skolans sätt att ha matematik, tre timmar i följd, ser Clark en fördel, och
det är att vid så långa lektioner finns det alltid tid att inkludera problemlösning, samt
laborativa övningar. För Clark är det bra att han väljer att variera undervisningen under dessa
tre timmar, där han ger akt på elevernas motivation: ”Vill de arbeta i matteboken, då får de
väl göra det.” Han säger också att om eleverna känner sig intresserade för utmaningar så får
de arbeta med större problem.
När det gäller IT-användningen är Clark väldigt positiv till det. Enligt honom använder
hans elever digitala hjälpmedel såsom datorer och miniräknare. Han tar upp som exempel
statistik, där han har låtit sina elever analysera och skapa diagram på dator. Ibland, när det är
32
passande till matematikområdet, säger Clark att laborativa övningar är ”fint komplement” till
det ”vanliga”.
5.3.3 Läromedel, läroplan och problemlösning
Clark förklarar att i Lgr 11, står det ganska informativt om förmågorna som varje elev ska
utvecklas i, där problemlösning är en del av detta. För Clark är läromedlen, till exempel
matematikboken, inte av central vikt: ”speciellt inte vid problemlösning.”. Han förklarar
vidare att uppgifter han väljer att använda sig av har kommit fram under tiden han har arbetat
som lärare, då han har samlat ihop en mängd material som han känner fungerar bra. Han säger
även att centrala prov, såsom nationella prov, har varit till hjälp i att hitta uppgifter. När vi
frågar om gamla läromedel och den nya läroplanen, får vi som svar att han tycker det är synd
att de inte följer Lgr 11, men att genom eget initiativ går det att undgå ett sådant problem. Han
tar även upp att det är en resursfråga, när och om nya läromedel, som är anpassade till Lgr 11,
kommer vara tillgängliga i skolan för alla elever.
5.4 Lärare: David
”Det blir dialoger i klassrummet, man hör olika tankar, olika strategier.”
David är ursprungligen från Sydeuropa där han avslutade sin grundskoleutbildning under 60talet. David tycker inte att det går att jämföra hans tid i skolan med hans elevers
grundskoletid. Han menar att kunskapskraven på hans tid var betydligt högre, samt att
lärorollen var annorlunda än idag. Läraren var den högsta auktoriteten med strikta
disciplinmetoder. Han är både utbildad ingenjör och lärare, med lärarutbildning i Sverige. Han
har sedan slutet av 90-talet arbetat i kommunal skola.
5.4.1 Synen på problemlösning
David börjar med att berätta att problemlösning för honom är ett sätt att låta eleverna utveckla
ett logiskt tänkande och att det ger de en möjlighet att se samband med verkligheten. Han
säger vidare att ett riktigt problem ska vara en utmaning för eleverna, med olika metoder och
strategier som kan leda till lösningen. Han fortsätter med att förklara att han anser att låta
33
eleverna arbeta med problemlösning är givande på grund av att det hjälper elever att använda
sina kunskaper i andra situationer, samt att det ”hjälper det logiska tänkandet” som för David
är viktigt inom matematiken.
5.4.2 Problemlösning i den egna undervisningen
Angående sitt sätt att arbeta under lektionerna, berättar David att i hans undervisning så
använder han den sista halvtimmen till att låta eleverna arbeta med problemlösning. Då
arbetar eleverna med problem med olika svårighetsgrader. Han förklarar att när han skapar
uppgifter och problem så använder han sina egna erfarenheter från det praktiska livet. Han
säger också att han använder sig mycket av det vardagliga i skapandet av problem så att
eleverna har lättare att komma in i problemet. David fortsätter med att säga att han låter
eleverna först arbeta individuellt med ett problem av lättare grad. Klarar eleverna problemet
får de gå vidare till något svårare. Klarar de inte problemet får de istället arbeta i par för att
försöka lösa det. David berättar sen att han avslutar sina lektioner genom att ha en gemensam
presentation framför tavlan. På så sätt får han fram dialoger kring matematiken ”använda det
matematiska språket”.
En metod som David använder i undervisningen är att låta eleverna själva skapa problem
utifrån det område de arbetar med. Detta hjälper, enligt David, honom att se på vilka nivåer
eleverna ligger på. Han berättar också att eleverna efter att de har skapat uppgifterna, går
igenom dem, antingen i helklass eller med läraren för att kunna se ”logiken” bakom det de
gjort. David försöker att anpassa problemen språkmässigt, så att det förstås av alla elever.
David tar sedan upp att många elever saknar språklig förståelse för de matematiska
begreppen. Som exempel tar han upp subtraktion, som vissa elever kallar för ”minusera eller
minusa”.
David berättar vidare att han ofta ”utnyttjar” elevernas ”tävlingsinstinkt”. Han organiserar
olika typer av tävlingar, som sker han anser alltid ska ske i grupper och aldrig individuellt. På
så sätt säger han att det ökar grupptillhörigheten och skapar en bra arbetsatmosfär. Han anser
att just detta moment är viktigt för eleverna eftersom det kommer att hjälpa dem i deras
arbetsliv. Han påpekar att klassrumsklimatet är viktig för att eleverna ska kunna arbeta,
speciellt då med problem. När det gäller laborativa övningar, säger David att det görs endast i
vissa områden, till exempel geometri, enheter och mönster och samtidigt tycker han att sådant
arbetssätt är givande, men krävande. David avslutar sättet han arbetar med att berätta att han
använder som hjälp både Youtube och Facebook. Facebook använder han till att ge
34
information om läxor och att få in dem. Youtube är perfekt, enligt David, för att med hjälp av
videoklippen kan han visa olika metoder att lösa matematiska uppgifter och problem.
5.4.3 Läromedel, läroplan och problemlösning
När vi börjar prata om läroplanen, berättar David att det är viktigt att kunna den och att de
centrala innehållen är bra att följa eftersom det är vad lärarna ska undervisa. Eftersom
problemlösning är en del av det, är det självklart för David att det ska vara med i det han lär
ut. Han berättar också att bedömningsmatrisen som finns i Lgr11 är lätt att följa och använda.
När det gäller matematikböcker, anser David att uppgifter som anknyter verkligheten till
elevernas vardag finns inte i så stor omfattning som det skulle behövas. Han säger också att
han inte följer matematikboken, men eleverna använder den till läxor och träningsuppgifter.
35
6. Analys
I följande avsnitt kommer vi att analysera data från våra intervjuer, samt de båda läroplanerna.
Huvudverktyg till analysen är Wyndhamns analytiska ramverk (figur 3), som använder sig av
de fyra lärandeteorier vilka vi beskrivit tidigare samt de två dimensionerna, tillämpning inlärning och arbetssätt - tankeprocess. På så sätt kommer våra undersökningsfrågor att
besvaras och analyseras. Vi vill betona att analysen av lärarnas berättelser inte kan ge en
helhetsbild av lärarna och vilka teorier som kan förknippas med dem och deras arbetssätt.
6.1 Lgr 11
Problemlösning framhävs tydligt och som viktigt i Lgr 11. Vidare så ska eleverna kunna
formulera, reflektera och värdera när de arbetar med problem (Skolverket, 2011). Tittar vi
närmare med hjälp av det analytiska ramverket kan vi se att Lgr 11 försöker omfatta olika
lärandeteorier i en helhet. Detta syns bäst i följande mening: ”Undervisningen ska bidra till
att eleverna utvecklar kunskaper för att kunna formulera och lösa problem samt reflektera
över och värdera valda strategier, metoder, modeller och resultat.” (Skolverket, 2011 s. 62).
Problemlösningsområdet fokuserar på att eleven som individ ska utveckla kunskaper genom
att reflektera och värdera, kunna formulera samt använda olika metoder, modeller och
strategier. Detta är aspekter knutna till individens kognitiva förmåga. Både kognitivismen och
konstruktivismen lägger stort fokus på att elever utvecklar kunskaper, till skillnad från
behaviorismen där kunskap istället endast ses som något inlärt. Konstruktivistiska drag visas
även av att matematikundervisningen ska stödja assimilering: ”Eleverna ska även ges
förutsättningar att utveckla kunskaper för att kunna tolka vardagliga och matematiska
situationer…” (Skolverket, 2011 s. 62). Elever ska även kunna beskriva och förklara
(kommunicera) problem vilket kan knytas till en samarbetsbetonad undervisning. Förutom
den individuella aspekten står det även i Lgr 11 om arbetet med vardagsanknutna problem
samt en betoning av samhällsenliga artefakter, såsom digitala verktyg vilket är områden som
den sociokulturella teorin anser som viktig.
Även om Lgr 11 på något sätt försöker kompromissa med de olika teorier, kan vi se att
problemlösning i skolan försöker luta mot att det viktiga i undervisningen är
tankeprocesserna, att det inte är resultatet som är det viktiga utan vägen till resultatet.
36
Samtidigt så ska arbetet med problemlösning undervisas på så sätt att eleverna både ska kunna
utveckla nya kunskaper samtidigt som tidigare kunskaper ska kunna tillämpas. Det ser vi
genom att problemlösning benämns både som en förmåga och som ett centralt innehåll.
6.2 International Baccalaureate Organization
IBO är väldigt detaljerad, i jämförelse med Lgr 11. I den står det att problemlösning ska ingå i
alla delar av matematiken (International Baccalaurate Organization, 2007). Det som
genomsyrar denna läroplan är att arbetet med problemlösning är en tankeprocess, där både
kognitivismen och konstruktivismen kommer fram. Begreppen reflektera och resonera tas
ofta upp i samband med problemlösning och ordet tänka används frekvent, som i till exempel:
”teachers should ensure that tasks allow students to think about the problem-solving
processes, reflect upon their methods and results” (International Baccalaurate Organization,
2007 s. 16). Matematikundervisningen ska sträva mot att förberedda elever så att de kan lösa
och analysera problem, både i skolan och i verkliga situationer. Vardagsanknytningen av
problemlösningen, samt kommunikationen mellan elever/lärare framhävs också och bär
tydliga spår av den sociokulturella teorin. IBO beskriver arbetet med problemlösning som en
integrerad del av matematiken och tyngden ligger på problemlösning som en tankeprocess,
och där liknande Lgr 11, att problemlösning ska både kunna utveckla nya kunskaper och
samtidigt ge möjlighet till att tillämpa tidigare kunskaper.
6.3 Anna
Anna har en syn på problemlösning som visar likheter med den läroplan hon följer. Både hon
och IBO anser att problemlösning ska arbetas med i kontexter för att efterlikna arbetslivet och
vardagen. Undervisningen ska betona reflektion och tänkande och det är begrepp som Anna
ofta tog upp. Eleverna ska enligt Anna kommunicera, reflektera och diskutera i matematiken
vilket sker antingen i helklass eller i grupper. Den sociokulturella teorin anser att
kunskapsutveckling sker i samspel med andra och genom det Anna berättar för oss, så innebär
mycket av hennes undervisning samarbete mellan elever. Detta visar på likheter med det
Vygotskij framhäver medan betoningen på reflektion och självständigt tänkande är begrepp
enligt Wyndhamns ramverk passande det kognitivistiska perspektivet. Anna berättade också
om användningen av digitala hjälpmedel som stöd till kunskapsutveckling i matematiken.
37
Vygotskij förklarade att miljön har en central roll i elevernas inlärningsprocesser där ”tools”, i
Annas fall datorer, används för att förmedla kunskap. Även om Anna lägger mycket fokus på
samarbete, kommunikation och reflekterande så finns det saker som Anna har sagt som kan
tolkas som drag från de andra teorierna. Till exempel att elever ska kunna hitta olika sätt att
lösa problem och att kunskap är onödigt om det inte kan användas i andra situationer. Elever
ska kunna assimilera tidigare kunskaper och erfarenheter till att lösa problem. Att Anna även
låter eleverna börja arbeta individuellt för att sen övergå till grupper skapar även det
paradoxer mellan de olika teorierna.
6.4 Ben
Ben berättar för oss vikten att som lärare kunna ”pusha” elever för att få dem att utvecklas
kunskapsmässigt genom att till exempel ge utmanande problem som eleverna arbetar med
antingen individuellt eller i grupp. Den kognitivistiska teorin anser att en elev ska ha
möjlighet att själv utveckla kunskap om att lösa problem, medan den sociokulturella teorin
anser att kunskapen utvecklas med hjälp av andra. Dock så blir det svårt att anknyta
arbetssättet till en viss teori då Ben inte berättar hur han som lärare agerar i de situationerna.
Han berättar också om vikten att utgå från elevernas erfarenheter och kunskapsnivåer, vilket
om vi sammanknyter med att ”pusha” elever, då med stöd av lärare och klasskamrater, kan
ses som en optimering av undervisningen. Det begrepp som kommer i åtanke är Vygotskijs
”zone of proximal development”, ett drag av det sociokulturella förhållningssätt vilket ger en
komplex bild av Bens undervisning.
Ben tar även upp att han använder sig av tävlingsmoment med belöningar. Syftet är att han
menar att det går att uppnå goda resultat vid tävlingar. Behaviorismen utgår från antagandet
att genom stimulus - respons metoden sker inlärning. Genom att vinna en tävling och få
belöning så gynnas ett visst beteende. Men det går inte att hänvisa Bens undervisning till en
särskild teori, utan det som han berättarvisar olika drag från olika teorier.
6.5 Clark
Clarks lektioner, utifrån det han berättar, ser ut på så sätt att lärandet sker som en social och
samarbetsbetonad aktivitet samtidigt som han också berättar att eleverna oftast startar arbetet
individuellt. Även om det sociala anses viktigt så berättar han att det är viktigt för den
38
individuella eleven att förstå problemen. De sociokulturella dragen, samarbete och
kommunikation finns där, men att eleven först med hjälp av egna erfarenheter och kunskaper
skapar ny förståelse är enligt Wyndhamn drag som anses komma från konstruktivismen.
Vygotskij till exempel lade stor vikt på att individens utveckling sker i samspel med
omgivningen vilket även Clark påpekar när han talar om att hans elever genom samarbete i
grupper har lättare att förstå och ”äger” då ett problem.
Clarks sätt att förklara sin roll som lärare visar likheter med Piagets syn att inlärning sker
genom individens tidigare erfarenheter vilket i Wyndhamns ramverk passar in med
konstruktivismen. Hos Clark visar det sig genom att han endast agerar som stöd och låtar
eleverna själva försöka hitta sina egna lösningsvägar vid problem. Dock så är inte det Clark
berättat för oss kongruent med en teori utan det finns samspel och spänningar mellan de olika
lärandeteorierna. Detta skulle eventuellt kunna förklaras med hans långa erfarenhet av yrket
samt den påverkan av olika pedagogiska undervisningsätt som förekommit under denna tid.
6.6 David
Davids sätt att tala om hur eleverna arbetar med problemlösning, där han betonar samarbete
och grupptillhörighet ger intryck av sociokulturella drag. I det perspektivet framhävs
kommunikation och inlärning genom andra. David pratar också mycket om ta vara på
elevernas tidigare erfarenheter samt att utveckla elevernas ”logiska tänkande”, vilket är
områden som Piaget betonade som viktiga i sin teori. I Wyndhamns ramverk skulle detta
tolkas som kognitivism. Möjligen skulle detta i Davids fall kunna ses som att samarbete är
något som ska stimulera elevernas motivation och deras tankeprocesser, alltså att samarbete är
ett medel för att nå ett kognitivt mål. David påpekade också hur han ofta anknöt matematiken
till arbetslivet samt lät eleverna själva skapa matematiska problem utifrån det område som
undervisades vilket är drag enligt Wyndhamn som pekar mot ett konstruktivistisk tänkande
snarare än ett sociokulturellt perspektiv. Att han sedan även berättar att hans elever kan
övergå från individuellt arbete till grupparbete skapar ytterligare svårigheter att kategorisera
Davids synsätt och arbetssätt till en specifik teori.
39
6.7 Jämförelse
För att fördjupa analysen kommer vi nu att försöka jämföra våra lärare i relation till både det
analytiska ramverk samt tidigare forskning om problemlösning. Vi kommer ta upp likheter
och skillnader som har hittats.
Lärarnas syn på problemlösning avspeglar sig i hur de berättar om genomförandet av sina
lektioner. Alla, förutom Anna, visar tendens där deras undervisning ställer krav på resultat
och att eleverna lär sig metoder och strategier som de sedan använder vid problemlösning,
men samtidigt så berättar alla att samarbete och diskussioner mellan elever är givande och
viktigt vid problemlösning. Detta visar att Anna är konsekvent med sin syn på problemlösning
och hur hon genomför sina lektioner i det, medan de andra lärarna skapar sina lektioner med
tydliga drag från andra teorier som inte är lika tydligt kopplade till deras syn på begreppet
problemlösning.
Något gemensamt hos de intervjuade lärarna är att de ser problemlösning som något med
anknytning till verkligheten. Verklighetsanknytningen tas upp i båda läroplanerna och i
tidigare forskning som en del av arbetet med problemlösning. Boaler (1998) fick fram hur
användningen av verklighetsbaserade problem hjälpte elever att se en bättre sammankoppling
mellan matematiken och vardagen samt att elever utvecklade bra strategier för att kunna lösa
problem. Alla lärarna tog också upp att det är oftast de själva som skapade problemen för sina
elever, där anpassning skedde för att passa elevernas vardag. Grevholm & Mouwitz (2000)
berättar hur dåligt anpassade problem inte fungerar för elever med dålig motivation, men även
för dem som har intresse för själva ämnet. Genom att lärarna själva skapar problemen med
anpassning till sina egna elevgrupper, kan det ses som ett försök att få eleverna engagerade i
problemlösning. Hela den här processen är också en idé från den sociokulturella teorin som är
för att främja en utveckling i matematiken med samhället som grund.
Alla lärare berättar också att de använder sig av grupparbete och diskussioner samt att de
vill att elever ska samtala med varandra när de arbetar med problemlösnig. Lärarna, förutom
Ben som brukar variera mellan arbete individuellt eller i grupper, startar med att ge ett
problem som eleverna ger sig in på individuellt, så att de sätter sig in i det för att sedan med
andra elever diskutera lösningsmetoder och resultat. Detta överrensstämmer med Hagland
m.fl.(2005) som betonar att grupparbete är ett viktigt segment i arbetet med problemlösning,
då samtalen mellan eleverna ökar förståelsen för matematiska begrepp och metoder. En annan
sak som är viktigt är att eleverna ska kommunicera och prata matematik med varandra och på
så sätt kunna hjälpa varandra med svårigheter vilket överensstämmer med Ahlberg (1991)
40
som betonar vikten att lärarna måste ge eleverna utrymme att verkligen prata och diskutera
matematik. Enligt Wyndhamns modell är det ett sätt att utveckla förståelse och få ny kunskap
som enligt Lester & Lambdin (2007) går hand i hand med problemlösnig.
Ett begrepp som alla lärarna tog upp, om än i olika omfattning, är samarbete. Alla lärarna
ansåg att undervisningen ska ge möjlighet för eleverna att samarbeta med varandra för att
utveckla kunskap. Det kan även anknytas till att det sker grupparbeten och kommunikation
samtidigt vilket lärarna anser ska utveckla förståelse för kunskapen. Även Lgr 11 och IBO tar
upp vikten av kommunikation och sociala interaktioner i undervisningen och det visas i det
lärarna berättar om problemlösning i deras undervisning.
Beskrivningar som har kommit upp vid intervjuerna med lärarna om problemlösning är till
exempel att problemlösning ska vara utmanande, det ska ha olika vägar att uppnå resultat, det
ska framhäva diskussioner och det ska vara lätt att förstå är beskrivningar som Hagland m.fl.
(2005) använder sig i en skildring av ett rikt matematiskt problem. Så även om
undervisningen av problemlösning skiljer sig åt kan det finnas likheter i hur ett problem ser
ut. Samtliga fyra lärare ser problemlösning som något bra och viktigt och beskriver det som
ett område med möjligheten att utveckla olika aspekter i matematiken.
41
7. Diskussion
Hela vårt arbete startade med att vi uppfattade att eleverna på den internationella skolan
visade mer engagemang och kunskap i matematik och då främst i problemlösning, än eleverna
i dem kommunala skolorna vi haft kontakt med. Det intressanta för oss var varför vi upplevde
en sådan skillnad och det medförde att vi ville undersöka detta vidare. Kunde vi hitta tydliga
skillnader som förklarade dessa upplevelser? Det vi har fått fram visar att det finns både
skillnader och likheter i läroplanen. Vår översiktliga analys av Lgr 11 är att den är allmän och
abstrakt, medan IBO uppfattade vi som mer detaljerad och konkret när det gäller
problemlösning. Begreppet problemlösning kommer oftare upp i IBO och då även i samband
med andra matematiska områden, medan i Lgr 11 står problemlösning för sig själv. Tittar vi
på våra lärare så finns det skillnader, men dessa skillnader upplevs inte så stora att de kan
förklara varför vi upplevde ett bättre engagemang och motivation i den internationella skolan.
Alla lärare berättade att de arbetar med problemlösning kontinuerligt och alla anser att det är
givande för eleverna. Men under arbetets gång har det kommit upp information som inte har
med själva lärarnas arbete med problemlösning att göra, utan är punkter som kan anses vara
mer socioekonomiska och resursbaserade.
Mycket av det lärarna sade om problemlösning och sättet de arbetar med det verkar på
något sätt idealt. Om det verkligen är på det här sättet är för svårt att säga då vi inte har följt
lärarna under deras lektioner. Det är naturligtvis också den begränsning som vår valda metod
med intervjuer ger. I intervjuerna har lärarna berättat om hur de planerar lektioner och
relaterar kanske också till lyckade exempel. Alla som själv har varit i klassrumsmiljön vet att
mycket kan inträffa som omkullkastar lärarens planering. Den erfarenhet som vi har från våra
kontakter med skolor är inte lika idyllisk. Våra erfarenheter säger att planeringen och den
goda intentionen ofta ersätts med arbete i läroboken.
En stor skillnad mellan skolorna som kom upp på intervjuerna är antalet
undervisningstimmar i matematik per vecka. Den internationella skolan har fyra timmar i
veckan medan den kommunala har tre timmar. Om det här förhållandet gäller under hela
grundskoletiden får eleverna i den internationella skolan markant mycket mer tid för
matematik. Detta är något som skulle kunna medföra att motivationen för problemlösning kan
upplevas högre i den internationella skolan. Om inte annat så har de åtminstone mer tid att
lägga på arbete med problemlösning.
42
En annan viktig skillnad mellan skolorna är att eleverna grupperas kunskapsmässigt i den
internationella skolan. Detta ansåg lärarna att det ger en möjlighet till att lättare skapa
undervisning för eleverna, samtidigt som dessa elever faktiskt får den hjälp de behöver för att
utvecklas, speciellt när det gäller elevgrupper med både hög och låg motivation. Alla lärare
tog upp att behöva anpassa undervisningen till alla elever är tidskrävande och kan medföra att
lektionerna inte kan utnyttjas till fullo.
Vidare kom det upp att den internationella skolan har större resurser till sitt förfogande.
Förutom de redan nämnda interaktiva medlen finns det även fler lärare, fem stycken fördelade
på 168 elever gentemot den kommunala där det finns fyra lärare fördelade på cirka 200
elever. Följden av detta är att klasserna i den internationella är mindre, vilket kan resultera i
bättre klassrumsklimat som möjligen kan medföra en högre motivation för matematiken.
Slutligen kan det även finnas en förklaring i elevernas sociala bakgrunder och deras
motivation till själva skolan. Eleverna i den internationella skolan är oftast barn till föräldrar
med hög utbildning och bra sociala förhållanden, medan i den kommunala skolan är många
elever nyanlända och många lever i familjer med sämre sociala förhållanden, där till exempel
socialbidrag krävs för att klara av vardagen. Det är något som Mella (2006) konstaterar,
nämligen att elever med sämre sociala förhållanden visar sämre resultat än elever som lever
under goda sociala förhållanden.
Men meningen med vår studie var inte att undersöka hur det sociala påverkar elevernas
resultat i skolan, utan vår fokus är matematiken och problemlösning. Samtidigt som vi
påpekar att det finns många faktorer utöver lärarnas syn på problemlösning som ger
förutsättningar för elevers lärande i matematik.
Resultaten som vi har fått från våra lärare kan vi inte generaliseras till landets lärare eller
skolformer utan är endast giltig för den undersökning vi har gjort. Som vidare forskning
skulle det vara intressant att undersöka de sociala bakgrunderna i relation till framgång i
matematiken, med fokus på vad som uppfattas som ett matematiskt problem i olika sociala
sammanhang. Det hade även varit intressant att undersöka elevernas syn på problemlösning
och deras uppfattning om dess betydelse i matematiken och samhället. För trots att såväl
lärare som läroplaner betonar verklighetsanknytning, så finns ju även de rent matematiska
problemen.
43
8. Referenser
Ahlberg, Ann. (1991). Att lösa problem i grupp, Emanuelsson, Göran m fl (red.):
Problemlösning. Studentlitteratur: Lund
Boaler, Jo. (1998). Open and Closed Mathematics: Student Experiences and Understandings,
Journal for Research in Mathematics Education vol.29, nr.1.
Bryman, Alan. (2011). Samhällsvetenskapliga metoder. Malmö: Liber AB.
Grevholm, Barbro & Mouwitz, Lars. (2000). Utmanande ändlösa additioner? Nämnaren nr.2.
Hagland, Kerstin, Hedrén, Rolf, Taflin, Eva. (2005). Rika matematiska problem – inspiration
till variation. Stockholm: Liber.
Hartman, Jan. (1998). Vetenskaplig tänkande: Från kunskapsteori till metodteori,
Studentlitteratur: Lund.
Helmertz, Tomoko. (2007). Problemlösning – en jämförelse mellan svensk och japansk
undervisning. Examensarbete. Malmö: Malmö högskolan/lärarutbildningen.
International Baccalaureate Organisation. (2007). Mathematics in the MYP
Kjeldstadli, Knut. (1998). Det förflutna är inte vad det en gång var. Lund: Studentlitteratur
Lester, Frank & Lambdin, Diana. (2007). Undervisa genom problemlösning. I Jesper Boesen
(red.), Lära och undervisa matematik – internationella perspektiv. Göteborg:
Nationellt Centrum för Matematikutbildning.
Mella, Orlando. (2006): Tre faktorer som tillsammans förklarar skolresultat i Sverige:
Socialklass, kön och etnicitet. Uppsala: Uppsala Univ.
Piaget, Jean. (1968). Barnets själsliga utveckling. Lund: Gleerups.
44
Ryen, Anne. (2004). Kvalitativ intervju. Malmö: Liber
Skolverket (2011). Läroplan för grundskolan, förskoleklassen och fritidshemmet 2011.
Stockholm: Skolverket.
Skoogh, Lennart & Johansson, Håkan. (1991). Att undervisa i problemlösning. I: Göran,
Emanuelsson; Bengt, Johansson & Ronnie, Ryding (red.) Problemlösning. Lund:
Studentlitteratur.
Strandberg, Lennart. (1991). Problem på olika nivåer. I: Göran, Emanuelsson; Bengt,
Johansson & Ronnie, Ryding (red.) Problemlösning. Lund: Studentlitteratur.
Vetenskapsrådet (2011). Forskningsetiska principer: Inom humanistisk-samhällsvetenskaplig
forskning. Hämtad 2013-10-21 från
http://www.vr.se/download/18.3a36c20d133af0c12958000491/God+forskningssed+2
011.1.pdf
von Glasersfeld, Ernst. (1990). An exposition of constructivism: Why some like it radical.
I:R.B. Davis, C. A. Maher & N. Noddings, (eds), Constructivist views on the teaching
and learning of mathematics. Journal for Research in Mathematics Education
Monograph No. 4. Reston, VA:NCTM, Inc, s. 19-29
Vygotskij, Lev Semjonovitj. (1978). Mind in society: The development of higher
psychological processes. (M. Cole et al.,Trans.) Cambridge, MA: Harvard University
Press.
Wyndhamn, Jan, Riesbeck, Eva & Schoultz, Jan. (2000). Problemlösning som metafor och
praktik. Linköping: Linköping University.
45
Bilaga 1
Intervjuguide
1. Presentation av oss själva och av arbetet
2. Inledningsfrågor om utbildning, arbetserfarenhet (Sverige/internationell), bakgrund
3. Tema 1: Vad är problemlösning för dig? Vad är din beskrivning av ett matematiskt
problem? Anser du problemlösning vara givande?
4. Tema 2: Hur planerar du en lektion med problemlösning? Vilka uppgifter väljer du
och varför? Hur arbetar du med problemlösning? För vilka har du problemlösning?
Arbetar ni med laborativa övningar under problemlösning? Arbetar ni individuellt,
grupp eller både och? Får alla elever arbeta med det eller en utvald grupp? I vilket
mån används IT-teknik i undervisningen?
5. Tema 3: Vad säger läroplanen om problemlösning? Hur mycket problemlösning är
representerad i läromedlen? Vad är skillnaden mellan läroplan och själva utförandet av
undervisningen av problemlösning? Vad är fördelarna/nackdelarna med IBO?
46