Geometriska begrepp i Linjär algebra

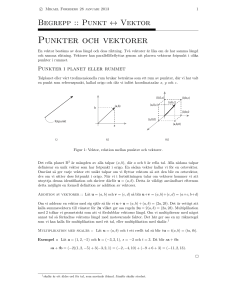
Geometriska begrepp i Linjär algebra
Introduktion
Vid uppgiftslösning i Linjär algebra
är det ofta fördelaktigt att rita en figur som hjälp. Här har några vanliga
geometriska begrepp samlats, illustrerade i enkla figurer. Förhoppningen
är att det här bladet ska leda dig rätt
och komma väl till pass under kursens gång, och att du när kursen är
slut inte längre skall behöva det mer.
Geometri i planet
I planet pratar vi om punkter, linjer
och vektorer. Nedan ser vi en punkt
𝑃 och en linje ℓ. Linjen ℓ fortsätter
förstås oändligt i båda riktningarna.
𝑃
𝐯
𝑃0
ℓ
En linje är också bestämd av två
punkter 𝑃0 och 𝑃1 . Givet dessa får
vi ju nämligen fram en riktningsvek→→→→→→
tor 𝐯 =𝑃0 𝑃1 .
𝑃1
𝑃0
ℓ
Plan (i rummet)
För att entydigt bestämma ett plan i
rummet räcker det att vi känner till
en punkt 𝑃0 i planet och två icke-parallella riktningar 𝐯1 och 𝐯2 som är
parallella med planet.
ℓ1
𝑃
ℓ2
ℓ3
Figuren ovan fungerar i både planet
och rummet. Om vi är i planet så
skär linjerna ℓ1 och ℓ3 nödvändigtvis
varandra. I tre dimensioner framgår
det inte av figuren.
Skärning mellan linje och plan
Om linjen ℓ inte är parallell med planet 𝜋 så skär ℓ och 𝜋 varandra i en
entydig punkt (𝑃 i figuren).
ℓ
ℓ
Geometri i rummet
I rummet behandlar vi punkter, linjer, plan och vektorer. Nedan ser vi
en punkt 𝑃 , en linje ℓ och ett plan
𝜋. Eftersom vi inte kan rita oändligt
stora figurer så ritar vi alltid bara en
del av linjer och plan.
𝜋
𝑃0
𝐯2
𝐯1
Det räcker också att känna till en
punkt 𝑃0 i planet och en normal 𝐧
till planet.
𝐧
𝑃
𝜋
ℓ
𝑃0
𝜋
𝑃
Om linjen och planet är parallella så
är det antingen så att de inte har
några gemensamma punkter alls (se
ℓ1 och 𝜋) eller så ligger linjen i planet
(se ℓ2 och 𝜋).
ℓ1
𝜋
Riktad sträcka, vektor
Två punkter 𝐴 och 𝐵 (i planet eller
rummet) bestämmer en riktad sträc→→→→→
ka 𝐴𝐵 från 𝐴 till 𝐵. Vektorer definieras som ekvivalensklasser av riktade sträckor där två riktade sträckor sägs vara ekvivalenta om den ena
kan fås genom parallellförskjutning
av den andra. I figuren nedan är den
→→→→→
riktade sträckan 𝐴𝐵 en representant
för vektorn 𝐮.
𝐵
𝐮
𝐴
→→→→→
Vi identifierar ofta 𝐮 och 𝐴𝐵 , och
→→→→→
skriver således 𝐮 =𝐴𝐵 .
Linje (i planet eller rummet)
Vad behöver vi veta för att bestämma
en linje? Till exempel räcker det att
känna till en punkt 𝑃0 på linjen och
en riktningsvektor 𝐯 (det vill säga en
vektor parallell med linjen).
Ett plan är även entydigt bestämt
om man känner till tre punkter 𝑃0 ,
𝑃1 och 𝑃2 i planet (som inte ligger
längs en linje). Vi känner ju då auto→→→→→→
matiskt två riktningar 𝐯1 =𝑃0 𝑃1 och
→→→→→→
𝐯2 =𝑃0 𝑃2 .
𝜋
𝑃0
𝑃1
𝑃2
Skärning mellan två linjer
Två linjer i planet skär varandra i
en punkt precis då de inte är parallella (se till exempel ℓ1 och ℓ2 som
skär varandra i punkten 𝑃 i figuren
nedan). Om två linjer i planet är parallella så finns två fall, antingen är
de samma linje eller så skär de inte
varandra alls (ℓ2 och ℓ3 i figuren nedan skär inte varandra).
För att två linjer i rummet skall skära
varandra i en punkt så är nödvändigt
men inte tillräckligt att de ej är parallella.
ℓ2
𝜋
Skärning mellan två plan
Även vid skärning av två plan kan tre
fall uppstå. Om planen 𝜋1 och 𝜋2 ej är
parallella så skär de varandra längs
en linje ℓ.
𝜋2
𝜋1
ℓ
Om 𝜋1 och 𝜋2 är parallella så kan de
antingen vara förskjutna och därmed
inte skära varandra alls
𝐱
𝑃0
𝜋1
𝜋2
𝐯
eller så är de parallella och sammanfaller helt.
𝜋1 = 𝜋 2
𝜋
𝐱′
Ortogonal projektion på linje
I figuren nedan är punkten 𝑃1 projektionen av 𝑃0 på ℓ. Det betyder att 𝑃1
är den punkt på ℓ som ligger närmast
𝑃0 .
𝑃0
𝑃1
Vid räkningar är det ofta smidigt att
se det som vektorer i stället för punkter. Den projicerade vektorn 𝐱′ nedan
erhålls genom att subtrahera projektionen av 𝐱 (med fotpunkt satt i planet 𝜋) på 𝐧 från 𝐱.
𝐧
Skalärprodukt
Skalärprodukten mellan två vektorer ger ett tal. Detta tal är positivt
om vektorerna ”pekar med varandra”,
noll om de är vinkelräta mot varandra (dvs. ortogonala) och negativt ”om
de pekar mot varandra”.
𝐯
𝐯
𝐮
𝐱
Spegling i plan
Att spegla en punkt 𝑃0 i ett plan 𝜋
innebär att man ska hitta en punkt 𝑃1
sådan att 𝑃0 och 𝑃1 ligger på samma
avstånd till 𝜋 och att linjen genom
𝑃0 och 𝑃1 är ortogonal mot 𝜋.
𝑃0
𝐮⋅𝐯<0
Vektorprodukt
Vektorprodukten, även kallad kryssprodukten, 𝐮 × 𝐯 är en vektor som
är ortogonal mot både 𝐮 och 𝐯. Dessutom ska det gälla att vektorerna 𝐮,
𝐯 och 𝐮 × 𝐯 är positivt orienterade.
Längden på 𝐮 × 𝐯 ges av arean av den
parallellogram som 𝐮 och 𝐯 spänner
upp.
𝐧
𝐱′
𝐮
𝐮⋅𝐯=0
𝐮⋅𝐯>0
𝜋
Ibland ser man det som att man projicerar vektorn 𝐱 (med sin fotpunkt
satt på linjen) på linjen ℓ. I själva verket är 𝐱′ nedan den ortogonala projektionen av 𝐱 på en riktningsvektor
till ℓ.
𝐯
𝐮
𝑃1
ℓ
𝐱
𝐱′
ℓ
𝜋
Spegling i linje
Punkten 𝑃1 nedan är speglinen av 𝑃0 i
linjen ℓ. Det betyder att 𝑃0 och 𝑃1 har
samma avstånd till ℓ och att linjen
genom 𝑃0 och 𝑃1 skär ℓ under rät
vinkel.
𝑃0
𝑃1
Även här är det ofta smidigt att arbeta med vektorer. Speglingen 𝐱′ av 𝐱
(med fotpunkt satt i 𝜋) i 𝜋 erhålls genom att från 𝐱 subtrahera två gånger
projektionen av 𝐱 på 𝐧.
𝐮×𝐯
𝐧
𝜋
𝐮
𝐯
I bilden ovan har vi ritat in 𝐮 och 𝐯
i ett plan, och understryker att 𝐮 ×
𝐯 är en normal till planet (dvs. den
är parallell med vilken annan given
normal 𝐧 som helst).
Ortogonal projektion
Den ortogonala projektionen 𝐱′ av en
vektor 𝐱 på en vektor 𝐯 är en vektor
parallell med 𝐯 och som berättar hur
mycket 𝐱 pekar i 𝐯:s riktning. Den
är vald så att vektorn 𝐱″ = 𝐱 − 𝐱′ är
ortogonal mot 𝐯.
ℓ
𝐱
𝜋
𝑃1
Även spegling kan vi åskådliggöra
med vektorer. Här är 𝐱′ speglingen
av 𝐱 (med fotpunkt satt på ℓ) i linjen
ℓ.
𝐱
𝐱′
Sned projektion
Ibland projicerar man inte ortogonalt
ner i ett plan utan längs en annan
given riktning 𝐯. I figuren nedan är
punkten 𝑃1 projektionen av punkten
𝑃0 ner i planet 𝜋 längs riktningen 𝐯.
𝑃0
ℓ
𝐯
𝐱′
Ortogonal projektion på plan
Att projicera en punkt 𝑃0 ortogonalt
ner i ett plan innebär att hitta den
punkt 𝑃1 i planet som ligger närmast
𝑃0 .
𝜋
𝑃1