Tentamen 2015-03-20 8:00
advertisement

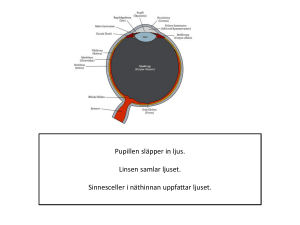
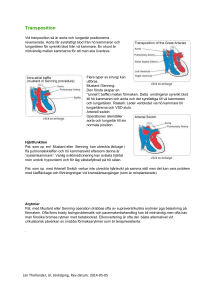
MVKF20 Transportfenomen i människokroppen Tentamen 2015-03-20 8:00-13:00 Obs! Tentamen är i två delar. Teoridelen (del A) skall lämnas in innan del B påbörjas. Hjälpmedel: Del A, inga hjälpmedel. Del B, kursbok, åhörarkopior från föreläsningar, föreläsningsanteckningar, lösta seminarietal, utdelat formelblad, TEFYMA, fysikaliska tabeller samt räknedosa. Egna lösta exempel eller sammanfattningar får ej användas. Maximalt antal poäng: 50. För godkänt krävs 22 poäng. Betygsgränser: 3 ≥ 22, 4 ≥ 32, 5 ≥ 42 Del A. Teorifrågor 1. a) Beskriv skillnaden mellan laminärt och turbulent flöde. b) Vilket dimensionslöst tal utnyttjas för att kvantifiera förutsättningar för laminärt respektive turbulent flöde? Vid vilket värde på detta tal sker övergången mellan de olika flödestyperna för flöde i ett cirkulärt rör? Var i luftvägarna är det störst sannolikhet att påträffa turbulent flöde, de grövre eller de finare luftrören? (2p) 2. 3. a) Nämn 3 förutsättningar som måste vara uppfyllda för att Bernoulli´s ekvation skall kunna tillämpas. b) Om tryckfallet i ett flöde genom en förträngning med givna dimensioner är känd, vad kan man då uppskatta med hjälp av Bernoulli´s ekvation? (2p) a) Vad innebär det att en vätska är Newtonsk? b) Vad är det i blodets sammansättning som gör att det är svårt att modellera blod som en newtonsk fluid? Vilka parametrar bör man ta hänsyn till om man vill bygga upp en noggrann materialmodell för blod? (2p) 4. Beskriv hur trycket i vänster kammare varierar under ett hjärtslag. Var noga med att i beskrivningen ange när aorta klaffen öppnar respektive stänger och hur blodflödet går under hjärtslaget. Förklara också varför man kan se ett litet backflöde i aorta under senare delen av hjärtslaget. (3p) 5. Ge exempel på 2 olika värmeöverföringsprocesser som förekommer mellan människokroppen och omgivningen. Ange vilka parametrar som styr förloppen. (3p) 6. a) Beskriv hur krökningen av ett blodkärl påverkar blodflödet genom det samma. b) Var är risken störst för plackbildning vid en Y-förgrening? Varför? (3p) 7. Utgå ifrån Fick´s andra lag, !!! !" = 𝐷!" ! ! !! !! ! , och ta fram ett uttryck för hur koncentrationen av substansen i varierar i ett tunt membran med tjockleken L. På membranets ena sida är koncentrationen 𝐶! och på den andra är den 𝐶! . I övergången mellan lösningen och membranets båda ytor gäller partioneringskonstanten 𝜙. Försumma konvektion och kemiska reaktioner och anta att det råder steady-state. (5p) MVKF20 Transportfenomen i människokroppen Del B. Problemlösning. 10 poäng per uppgift. B1. En person åker bil med sin nakna underarm stickande utanför bilen. Bilen färdas med 50 km/h. Omgivningens temperatur är 0˚C och lufttrycket är 1 atm. Underarmen kan approximeras som en cylinder med längd 30 cm och omkrets 25 cm. Vidare antas att armens tvärsnitt kan indelas i två zoner där den inre har en konstant temperatur 37˚C. Den inre delens diameter är 80 % av armens diameter. Konduktiviteten den yttre delen av armen är 0,41 W/(m·K). Värmeövergång från handen kan försummas eftersom personen bär handskar. Konduktiviteten för luft vid 0˚C är 0,0243 W/(m·K) och viskositeten för luft 1.71·10-5 Pa·s Beräkna armens yttertemperatur samt värmeflödet. Antag stationärt tillstånd. B2. Möss används ibland som modell vid studier av kardiovaskulära sjukdomar hos människor. Ett forskarlag har därför bestämt sig för att studera blodströmningsfenomen i en musaorta. De bygger därför en laboratoriemodell av aorta i skala 5:1. Till detta kopplas en pulserande pump för att simulera hjärtat. I försöken används en fluid med densiteten 1800 kg/m3 och en viskositet 0,017 Pa·s. Eftersom skjuvspänningen, τ, med vilken blodströmningen belastar endotelet har visat sig ha en inverkan på sjukdomsförloppet vill man mäta denna. I tabellen nedan finns några data för musen. hjärtfrekvens, ω (slag/min) flöde från hjärtat, Q (l/min) densitet, ρ (kg/m3) viskositet, µ (Pa·s) 650 0,026 1005 0.0035 Skjuvspänningen kan således beskrivas som 𝜏 = 𝑓 𝑄, 𝜌, 𝜇, 𝜔, 𝑑 där d är kärlets diameter. a) Finn med hjälp av Buckinghams Pi-teorem lämpliga dimensionslösa grupper, dvs. finn ett uttryck för det dimensionslösa tryckfallet och vilka dimensionslösa tal den beror av. Ledning: Eftersom τ söks är det lämpligt att inte låta den ingå i basgruppen. b) Beräkna den pumpfrekvens och det flöde som krävs för att strömningsförhållandena i laboratoriemodellens ska överensstämma med de som råder i musens aorta. c). Om skjuvspänningen 35 dyn/cm2 uppmäts i en viss position i laboratoriemodellen, vilken skjuvspänning motsvarar det vid motsvarande position i musaortan? 1 dyn = 1·10-5 N MVKF20 Transportfenomen i människokroppen B3. Makuladegeneration är en sjukdom i näthinnan som påverkar den centrala delen av synfältet. En föreslagen ny behandling går ut på att en löslig pellet innehållande läkemedlet placeras i centrum av ögats glaskropp och läkemedlet diffunderar till näthinnan. Diffusionskoefficienten är 1·10-7 cm2/s. Antag att ögat kan modelleras som en sfär med radien 1 cm och att pelletten har en radie på 3 mm. Läkemedelskoncentrationen i pelletten är 10 mg/ml. Bortse från vad som händer i främre delen av ögat och försumma näthinnans tjocklek. a) Gör en grov uppskattning av hur lång tid det tar för läkemedlet att nå från pellet till näthinna. b) När läkemedlet når näthinnan kommer den mängd som inte tas upp i näthinnan att omedelbart transporteras bort genom bakomliggande vävnad. Således kan läkemedelskoncentrationen på näthinnans yta betraktas som konstant lika med noll. Vidare får antas att pellettens storlek är konstant. Uppskatta tiden det tar innan allt läkemedel är borta från ögat. Lycka till!