Занятие 4
advertisement

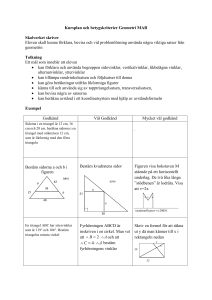
Lektion 9. Vinklar och deras summor Fakta. Summan av (de inre) vinklarna i n–hörning är 180(n–2). Summan av de yttre vinklarna är 360. Upp 1. Bestäm vinkel i en regelbunden n–hörning. Upp 2. Bestäm summan av de 5 markerade vinklarna i en femuddig stjärna. Upp 3. Man drar två diagonaler från ett hörn till ändpukterna på den motsatta sidan i en regelbunden 45-hörning. Bestäm vinklaran i triangeln som är bildat av de diagonlerna samt den sidan. Upp 4. Ett antal diagonaler dras i en n–hörning some ej skär varandra. Diagonalerna delar n–hörningen i trianglar. Bestäm antalet trianglar. Problem 5. Bestäm det största antalet spetsiga vinklar som kan påträffas i en konvex polygon. Sats 6 (Eulers formel) En polygon är indelad i trianglar på ett sådant sätt att ingen triangel har ett hörn inne på sidan av polygonen eller en annan triangel. Låt det finnas totalt H hörn, K sidor samt S trianglar. Så gäller H–K+S=1. Problem 7. Bestäm alla värden som den näst största vinkeln kan anta i en konvex а) fyrhörning b) n-hörning. Problem 8. Bestäm det minsta antalet rektanglar som polygonen på bilden kan delas i. a) Man får klippa endast längs rutornas kanter; b) Man får klippa hur som helst. Problem 9. Kan man dela en kvadrat i trianglar på ett sådant sätt att varje triangel angränsar längs en sträcka a) med exakt tre de andra? b) med minst fyra de andra? Problem 10*. Ur en rektangulärt pappersblad är klipps ut n rektangulära hålor med kanterna parallella med bladets kanter. Bestäm det minsta möjliga antalet rektanglar som man kan garanterat dela det håliga bladet. Problem för den kontinuerliga mattedrabbningen M13. Kan man dela en kvadrat i likbenta trianglar med två vinklar 75 i varje triangel? M14. En polygon kan delas i 100 rektanglar men kan ej delas i 99 rektanglar. Visa att polygonen kan ej delas i 100 trianglar. Mattecirkeln http://shap.homedns.org/sks/svenska/ 3 november 2007 Ledaren Alexandre Chapovalov [email protected]