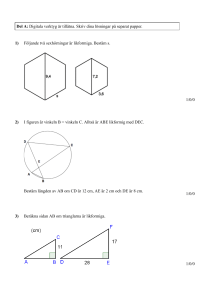
Problem

Lektion 15. Likformiga trianglar
Definition. Två trianglar kallas likformiga om deras motsvarande vinklar är lika och deras
motsvarande sidor är proportionella. Närmare bestämt, ABC ~ A' B' C' om A=A’,
AB
AC
BC


B=B’, C=C’ och
=k. Förhållandet k kallas i så fall för likformighets
A' B' A' C ' B' C '
koefficient, och man säger att den 1:a triangeln är likformig till den 2:a med koefficienten k.
Upp 1. Visa att kongruenta trianglar är likformiga till varandra. Bestäm koefficienten.
Upp 2. Givet att ABC ~ A' B' C' . Det är känt att AB=9, AC=12,
A’C’=6, B’C’=5. Bestäm likformighetens koefficient samt A’B’ och BC.
Sats 3. (3:e likformisfallet: Två vinklar (utan bevis) Om två vinklar i en
triangel är lika med två vinklar i en annan triangel så är trianglarna
likformiga mot varandra. D.v.s. om A=A´, B=B´ så är
ABC ~ A' B' C' .
Sats 4. (Topptriangelsatsen) Om MN||BC (se bilden) så är ABC 
AMN.
Lemma 5. Om AM/AB=AN/AC (se bilden) så är MN||BC.
Sats 6. (1:a likformisfallet: två sidor och mellanliggande vinkel)
Om AB/A´B´=AC/A´C´, A=A´ så är ABCA´B´C´.
Sats 7. (2:a likformisfallet: Tre sidor) Om AB/A´B´=AC/A´C´=BC/B´C´ så är ABCA´B´C´.
Upp8. a) C=90. Visa att höjden CH (se bilden) dragen
mot hypotenusan delar den stora triangeln i två mindre
trianglar som är likformiga till den stora samt till
varandra.
b) Givet att AC=4, BC=3. Bestäm AH, BH, CH.
Prob9. Visa att CH  AH  BH på bilden.
Definition. En sträckan som binder samman två sidornas mittpunkter i en triangel kallas
medellinje.
Upp 10. Visa att en medelinje är parallel med den 3:e sidan och är hälften så stor.
Upp 11. Kordor AN och BM skär varandra i en punkt P inom cirkeln. Visa att ABPNMP.
Upp 12. Inom ABC dras höjderna AH och BK. Visa att tringeln HKCABC.
Poänguppgifter (Lamnas in senast om två veckor).
15-1. Två trianglar är likformiga till varandra med koefficient k. Visa att motsvarande
a) höjder; b) bisektriser
står i samma förhållande k mot varandra.
15-2. Kordor AN och BM skär varandra i en punkt P inom cirkeln. Visa att PAPN=PBPM.
15-3. Givet en cirkel samt en punkt P utanför cirkeln. En tangent genom P tangerar cirkeln i en
punkt A. En rät linje skär cirkeln i punkter B och C. Visa att PCPB=PA2.
Den 14 mars 2008, Metapontum, åk1 http://sasja.shap.homedns.org/Metapontum/2007/vt1/