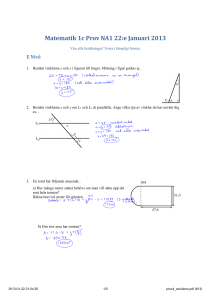
Del A: Digitala verktyg är tillåtna. Skriv dina lösningar på separat papper.
1)
a) Bestäm vinkeln x.
b) Vilket eller vilka av följande geometriska samband använde du då du bestämde
vinkeln x?
Endast svar fordras.
A Pythagoras sats
B Vinkelsumman i en triangel är 180° .
C Summan av sidovinklar är 180° .
D Yttervinkelsatsen
E Topptriangelsatsen
F Randvinkelsatsen
2/0/0
2)
Bestäm triangelns vinklar
2/0/0
3)
Linjerna L och L är parallella. Bestäm vinklarna markerade x och y.
1
2
2/0/0
4)
De två linjerna är parallella. Vinkel y är 60°. a) Bestäm vinkel x
b) Bestäm vinkel z
2/0/0
5)
I en rätvinklig triangel är hypotenusan 25 cm och den ena kateten är 4 cm längre än
den andra.
Bestäm triangelns area.
0/2/0
6)
I den rätvinkliga triangeln ABC dras höjden h mot hypotenusan AB. Höjden delar
hypotenusan i två delar som i figuren betecknas med x och v.
Visa att h
−
−
−
−
−
= √x × v
0/2/2
Bedömningsanvisningar
1)
a)
40°
Redovisad godtagbar lösning.
+ ER
b) D eller B och C
Korrekt svar utifrån lösningen i frågan a).
+ ER
33°, 48° och 99°
Korrekt uppställd ekvation, påbörjad lösning.
+ EB
Korrekt lösning och tydlig redovisning. + EP
Vinkel x = 136° och vinkel y = 44°
Korrekt bestämning av en vinkel
+ EB
Korrekt bestämning av båda vinklarna
+ EB
2)
3)
4)
a) 120°
Korrekt svar
+ EB
b) 60°
Korrekt svar
+ EB
150 cm
Redovisad godtagbar ansats, t ex korrekt uppställd ekvation
+ CPL
med redovisad godtagbar lösning med korrekt svar.
+ CPL
5)
2
; 152 cm
2
6)
Redovisad godtagbar ansats, t ex visar att en deltriangel är likformig
med triangeln ABC eller tecknar en korrekt ekvation med hjälp av
likformighet.
+ CPL
Slutför beviset men motiveringar kan vara ofullständiga, t ex visar inte
att deltrianglarna är likformiga men genomför beviset korrekt i övrigt.
(Elevlösningar som bygger på Pythagoras sats bedöms på motsvarande
sätt).
+ CR
Genomför beviset med fullständiga motiveringar.
+ AR
Genomför beviset välstrukturerat med ett i huvudsak korrekt
matematiskt språk.
+ AK
