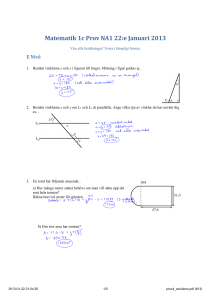
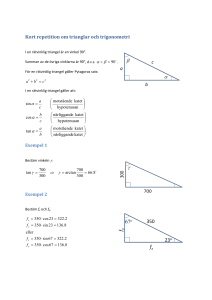
MAA 3.1 Kursprov våren 2012
ERA
Lös 8 uppgifter. Skriv ditt namn på varje papper. Varje uppgift är värd max 6 poäng.
1. a) Hypotenusan i en rätvinklig triangel är 10 och den ena kateten är 8. Bestäm längden av den
andra kateten och storleken av de spetsiga vinklarna med en grads noggrannhet.
b) Bestäm vinkeln α i figuren.
310°
91°
α
2. Nedan är en bild av bakfönstret på en bil samt spåret av vindrutetorkaren? Hur stor är ytan som
hålls ren av vindrutetorkaren?
170°
10 cm
28 cm
3. a) Sidorna i en triangel är 9, 20 och 25. Bisektrisen till den minsta vinkeln delar den motstående
sidan i två delar. Bestäm längden av dessa delar.
b) En median i en triangel har längden 24. Bestäm längden av de delar i vilka de övriga medianerna
delar denna median.
VÄND!
4. En tomt har formen av en parallellogram med sidorna 110 m och 62 m. Vinkeln mellan dessa
sidor är 65°.
a) Bestäm längden av tomtens diagonaler.
b) Bestäm arean av tomten. Ge svaret i hektar.
5. Cirkelns radie är 8,0 m och triangelns hörnpunkter A, B och C ligger på cirkelns rand.
Beräkna längden AB.
A
C
106°
23°
B
6. En cirkel omskriver en liksidig triangel så att triangelns hörn ligger på cirkeln. En annan cirkel
inskrivs i triangeln så att den tangerar triangelns sidor. Hur många procent större är den förra
cirkelns area än den senares?
7. Bevisa bisektrissatsen.
8. Två sfärer har radierna 10 cm respektive 25 cm och deras medelpunkter ligger på avståndet 20
cm från varandra. Bestäm volymen på den kropp som utgörs av punkterna som ligger innanför
bägge sfärer.
9. Om man förenar sidornas mittpunkter med hörnen i en kvadrat uppstår i mitten en figur som ser
ut som en regelbunden åttahörning. Visa med uträkningar att figuren inte är regelbunden.
10. Följande gäller för en rätvinklig triangel: den ena katetens projektion på hypotenusan är lika
lång som den andra kateten. Bestäm triangelns vinklar med en grads noggrannhet.
