Föreläsning 3/10 Potentialteori Mats Persson 1 Bestämning av
advertisement

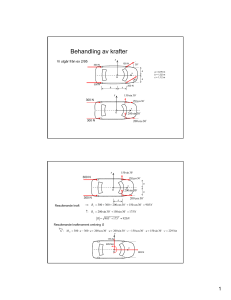
Föreläsning 3/10 Potentialteori Mats Persson 1 Bestämning av elektriskt fält Elektrostatikens ekvationer: Det elektrisk fältet E bestäms av laddningsfördelningen ρ via Gauss sats I Z 1 E · dS = ρdV (1) ²0 V S eller uttryckt på differentialform ∇·E= ρ . ²0 (2) Det statiska elektrisk fältet är virvelfritt, ∇ × E = 0, så det finns en elektrostatisk potential φ dvs E = −∇φ. Denna potential satisfierar då Poisson’s ekvation ρ ²0 (3) ρ(r0 ) dV 0 . 4π²0 |r − r0 | (4) ∇2 φ = − som har den allmänna lösningen Z φ(r) = Exempel: En elektrisk laddning q är jämnt fördelad i en sfär med radien a. Den omges av ett tunt sfäriskt skal med radien 2a och laddningen −q. Bestäm det elektriska fältet E(r) och potentialen φ(r) överallt. Lösning: På grund av att laddningsfördelningen har sfärisk symmetri, så beror potentialen φ enbart påradien r vilket medför att E = −∇φ(r) = − ∂φ ∂r r̂ = Er (r)r̂, dvs elektriska fältet är riktat i radiell led och beror enbart på radien. Vi kan då beräkna Er (r) med hjälp av Gauss lag I Q E · dS = , (5) ²0 S där vi låter S vara en sfär, och Q är den laddning som innesluts av S. Om vi börjar med fallet att S har en radie r > 2a, så ser vi då att den totala inneslutna laddningen är q − q = 0. Alltså har vi att I E · dS = 0, (6) S och av detta följer att att Er = 0. Om S har en radie r så att a < r < 2a, så är den laddningen, som S innesluter, q. Då ger oss Gauss lag att I q E · dS = . (7) ²0 S Integralen i vänsterledet har värdet I E · dS = 4πr2 Er , (8) S och vi kan lösa ut Er = 1 q . 4π²0 r2 1 (9) Slutligen har vi fallet att sfärens radie r < a. Eftersom laddningen q är jämt fördelad över volymen, så innebär det att S innesluter laddningen q Gauss lag ger oss alltså ³ r ´3 a I E · dS = S vilket blir Er = q ³ r ´3 , ²0 a q ³ r ´3 . ²0 a 4πr2 Er = Vi kan nu lösa ut . 1 qr . 4π²0 a3 Om vi nu sammanfattar våra resultat, så har vi för det elektriska fältet 1 qr r<a 4π²0 a3 1 q a < r < 2a Er = 2 4π²0 r 0 r > 2a (10) (11) (12) (13) (14) Vi skall nu utnyttja detta för att bestämma potentialen, eftersom Er (r) = − ∂φ ∂r . Således kan vi uttrycka potentialen som integralen Z ∞ φ (r) = Er dr, (15) r vilket sätter potentialen till 0 i oändligheten i enlighet med den vanliga konventionen. Vi börjar då med att bestämma potentialen för intervallet r > 2a. Eftersom Er = 0 här så följer det att också potentialen blir 0. I intervallet a ≤ r ≤ 2a så kan den övre integrationsgränsen sättas till 2a, eftersom potentialen är 0 utanför. · ¸2a µ ¶ Z 2a q 1 q 1 1 1 q dr = − = − . (16) φ (r) = 4π²0 r2 4π²0 r r 4π²0 r 2a r Speciellt så lägger vi märke till att potentialen i punkten r = a blir φ (a) = q . 8π²0 a (17) Vi kan nu uttnyttja detta värde för att räkna ut integralen för r ≤ a påföljande sätt · ¸a Z ∞ Z a qr q qr2 φ (r) = Er dr = φ(a) + dr = + = 3 8π²0 a 8π²0 a3 r r r 4π²0 a q qr2 q qr2 q 2a2 − r2 q + − = − = . 3 3 8π²0 a 8π²0 a 8π²0 a 4π²0 a 8π²0 a 8π²0 a3 Vi kan till slut sammanfatta potentialen som q 2a2 −r2 r≤a 8π²0 ¡ a3 ¢ q 1 1 φ (r) = − a ≤ r ≤ 2a 4π²0 r 2a 0 r ≥ 2a 2 (18) (19) 2 Bestämning av ett magnetfält Magnetostatikens ekvationer: Det magnetiska fältet B bestäms av strömfördelningen j via Ampere’s lag I Z B · dr = µ0 j · dr (20) C S eller uttryckt på differentialform ∇ × B = µ0 j. (21) Det magnetiska fältet är källfritt, ∇ · B = 0, så det finns en vektor potential A dvs B = ∇ × A och kan fixeras med villkoret ∇ · A = 0. Denna potential satisfierar då Poisson’s ekvation på vektor form ∇2 A = −µ0 j (22) som har den allmänna lösningen Z A(r) = µ0 j(r0 ) dV 0 . 4π|r − r0 | (23) Exempel: En oändligt lång rak ledare har ett cirkulärt tvärsnitt med radien a och leder en likström med strömstyrkan I. Använd Amperes lag för att härleda magnetfältet i och kring ledaren om materialet i den antas homogent och isotropt. Lösning: Eftersom vi har en axialsymmetrisk strömfördelning riktad i z-riktningen så kan vektorpotentialen uttryckas A = A(ρ)ẑ. Detta medför att B = ∇ × A = ∇A × ẑ = ∂A ∂ρ ρ̂ × ẑ = − ∂A ϕ̂ = B (ρ) ϕ̂ dvs magnetfältet är riktat i ϕ-riktningen och beror enbart påavståndet från ϕ ∂ρ ledaren. Vi kan då använda Amperes lag I B · dr = µ0 I, (24) C där vi låter C vara en cirkel kring z-axeln, och I är strömmen som passerar genom den yta som har C som rand. Först tittar vi på fallet att cirkelns radie ρ > a. Strömmen är då I, och Amperes lag ger oss I B · dr = µ0 I. (25) B · dr = 2πρBϕ . (26) C Integralen blir då I C Vi kan nu lösa ut Bϕ = µ0 I . 2πρ (27) I fallet att cirkelns radie ρ < a så antar vi att strömmen är jämnt fördelad i tråden, vilket ger oss att den inneslutna strömmen blir ³ ρ ´2 I . (28) a Integralen blir nu I ³ ρ ´2 B · dr = 2πρBϕ = µ0 I . (29) a C Vi kan då lösa Bϕ = µ0 I ρ . 2π a2 (30) Sammanfattningsvis har vi alltså ( Bϕ = µ0 I 2πρ µ0 Iρ 2πa2 3 ρ<a ρ>a (31) 3 Lösning av Poisson-ekvation PLK Kap. 6.1, Uppg. 10: I sfären med radien r = a finns en rymdladdning med tätheten r ρ (r, θ, ϕ) = ρ0 sin θ cos ϕ, a (32) och på sfären gäller att Φ (a, θ, ϕ) = Φ0 . Bestäm den elektrostatiska potentialen Φ och det elektriska fältet E inuti sfären. Lösning: Poissons ekvation ger oss att ∇2 Φ = − ρ0 r sin θ cos ϕ ²0 a (33) med randvillkoret att Φ (a, θ, ϕ) = Φ0 . Vi ser här att randvillkoret är sfäriskt symmetriskt, men att källan har ett vinkelberoende av formen sin θ cos ϕ. Med uttnyttjandet av linjär superposition kan vi då ansätta en lösning som består av två delar, vilka var och en har en av dessa egenskaper Φ = f (r) + g (r) sin θ cos ϕ. (34) Om vi applicerar Laplace-operatorn på Φ så får vi µ ¶ µ ¶ 1 ∂ 1 ∂ ∂Φ 1 ∂2Φ 2 ∂Φ r + sin θ + = 2 r2 ∂r ∂r r2 sin θ ∂θ ∂θ r2 sin θ ∂ϕ2 ¤ 1 ∂ £ 2 0 1 ∂ 1 r (f + g 0 sin θ cos ϕ) + 2 [sin θ (g cos θ cos ϕ)] + 2 2 (−g sin θ cos ϕ) = 2 r ∂r r sin θ ∂θ r sin θ ¤ £ ¡ ¢¤ 1 £ 1 g cos ϕ 2r (f 0 + g 0 sin θ cos ϕ) + r2 (f 00 + g 00 sin θ cos ϕ) + 2 g cos ϕ cos2 θ − sin2 θ − 2 = r2 r sin θ r sin θ ¶ µ 0 ¶ µ 2 0 g g cos θ 1 f − sin θ − . (35) 2 + f 00 + 2 + g 00 sin θ cos ϕ + 2 cos ϕ r r r sin θ sin θ Vi beräknar uttrycket i den sista parentesen 1 cos2 θ − sin2 θ − cos2 θ − sin2 θ cos2 θ − sin θ − = = −2 sin θ. sin θ sin θ sin θ Alltså kan vi skriva Poissons ekvation som µ ¶ f0 g0 g ρ0 r ∇2 Φ = 2 + f 00 + g 00 + 2 − 2 2 sin θ cos ϕ = − sin θ cos ϕ. r r r ²0 a (36) (37) Eftersom den här ekvationen skall gälla för alla värden på θ och ϕ så ger oss detta ekvationerna ( 0 f 00 + 2 fr = 0 0 (38) g 00 + 2 gr − 2 rg2 = − ρ²00 ar Vi börjar med att lösa ekvationen för f genom att ansätta en lösning på formen f = Arν , men konstanten A kan vi utelämna för tillfället, så att f 0 = νrν−1 och f 00 = ν(ν − 1)rν−2 . Detta ger oss ekvationen ν (ν − 1) rν−2 + 2νrν−2 = 0, (39) som förenklas till ν 2 + ν = 0, (40) som har lösningarna ν = 0 och ν = −1. Därför får vi f (r) = A + B . r (41) Här måste vi sätta B = 0, för att undvika att potentialen blir oändlig för r = 0, och A = Φ0 för att vi ska uppfylla randvillkoret Φ(a, θ, ϕ) = Φ0 . 4 Vi går nu över till ekvationen för g och börjar med att bestämma en partikulärlösning på formen g = Cr3 . För denna lösning har vi g 0 = 3Cr2 och g 00 = 6Cr, vilket ger oss 6Cr + 6Cr − 2Cr = − som har lösningen C=− ρ0 r , ²0 a (42) 1 ρ0 , 10 ²0 a (43) 1 ρ0 r 3 . 10 ²0 a (44) och partikulärlösningen är alltså g (r) = − Vi behöver också bestämma lösningen till den homogena ekvationen, och därför ansätter vi g(r) = Drν , men för ögonblicket utelämnar vi konstanten D. Eftersom g 0 = νrν−1 och g 00 = ν(ν − 1)rν−2 , så får vi ν (ν − 1) rν−2 + 2νrν−2 − 2rν−2 = 0, (45) vilket ger oss andragradsekvationen ν 2 + ν − 2 = 0. Denna har lösningarna 1 ν=− ± 2 sµ ¶ 2 1 1 3 +2=− ± . 2 2 2 (46) (47) Alltså har vi ν = −2 och ν = 1, så den allmänna lösningen för g blir g (r) = 1 ρ0 r3 D + Er − . r2 10 ²0 a (48) Vi sätter D = 0 eftersom potentialen inte kan bli singulär i r = 0. Vårt randvillkor vid r = a säger oss å andra sidan att g(a) = 0, vilket ger oss 0 = Ea − så att E= 1 ρ0 2 a , 10 ²0 1 ρ0 a 10 ²0 (49) (50) Alltså är potentialen Φ (r, θ, ϕ) = Φ0 + 1 ρ0 2 ³ r r ´ a − ( )3 sin θ cos ϕ. 10 ²0 a a (51) Vi kan nu beräkna det elektriska fältet ur µ ¶ ∂Φ 1 ∂Φ 1 ∂Φ E = −∇Φ = − r̂ + θ̂ + ϕ̂ = ∂r r ∂θ r sin θ ∂ϕ · µ ¶³ ´¸ 2 2 1 ρ0 r a r − a −3 2 sin θ cos ϕr̂ + − 2 cos θ cos ϕθ̂ − sin ϕϕ̂ 10 ²0 a r a 5 (52)