En ohanterlig parallellogram

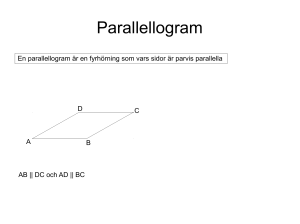
En ohanterlig parallellogram
Per Häggmark
I Nämnaren nr 3/4,1990 refererades en rapport från en konferens i Helsingfors om geometriundervisning . En ungersk examensuppgift föreföll
särskilt intressant och får här en utförlig och spännande belysning.
För många år sedan refererade jag i Nämnaren en rapport om en konferens i Helsingfors om geometriundervisning. Under
arbetet med rapporten råkade jag observera en detalj i denna som föreföll mig särskilt intressant. Det gällde en examensuppgift från Ungern, presenterad av Dr Andreas Ambrus vid institutet för matematik
i Budapest. Uppgiften handlar om beräkning av en parallellograms area. Kanske
framgår det så småningom varför detta till
synes triviala problem intresserat mig.
förväntades prestera eller vilka krav på lösningens kvalitet som gällde. Möjligen förekom diskussioner om detta i Helsingfors,
men det nämns inte i rapporten.
Låt oss beskriva den i rapporten framlagda lösningen
x
b
y
α
x
y
a
Examensuppgiften
Problemtexten verkar alldaglig och oförarglig, och lyder som följer:
Sidorna i en parallellogram är
3 respektive 1 längdenheter.
Diagonalerna skär varandra
under 45º vinkel. Beräkna
parallellogrammens area.
I rapporten redovisas endast texten ovan
och en kortfattad elegant lösning, som vi
strax skall återge. Det saknas diskussion
om syftet med uppgiften. Inte heller berättar författaren om vilken lösning eleverna
Per Häggmark är universitetslektor emeritus i ämnesteori och ämnesmetodik i
matematik. Detta är hans 20:e artikel i
Nämnaren.
Nämnaren nr 1, 2000
Vi inför allmänna beteckningar:
– Parallellogrammens sidor är a och b
längdenheter, där a > b.
– Diagonalerna, som i en parallellogram
skär varandra mitt itu, är 2x och 2y
längdenheter.
– Den spetsiga vinkeln mellan
diagonalerna är α º.
– Parallellogrammens area är A areaenheter.
Diagonalerna delar parallellogrammen i
fyra trianglar, vars areor är lika stora. Med
hjälp av cosinussatsen får vi sambanden:
A = 2xy sin α
(1)
x 2 + y 2 + 2xy cos α = a 2
(2)
x 2 + y 2 − 2xy cos α = b 2
(3)
57
Subtraktionen (2) – (3) ger:
4xy cos α = a2 − b 2
(4)
Vi går över till det speciella fallet a = 3,
b = 1 och α = 45º. Insättning i (1) respektive (4) ger:
A=
4xy
2xy
= 9 −1
och
2
2
Vi har förutsatt att mätetalen x och y är
reella tal. Enligt ”lösningen” är A = xy 2 .
Om x och y vore icke-reella tal, kan mycket väl xy vara ett reellt tal, men i det fallet
kan produkten xy 2 inte tolkas som arean av en parallellogram. Det finns skäl att
misstänka att ekvationssystemet nedan har
icke-reella lösningar:
x 2 + y 2 + 2xy ⋅
1
=9
2
(2)
x 2 + y 2 − 2xy ⋅
1
=1
2
(3)
vilket ger:
xy =
8 2
= 2 2 och A = 4
4
En förträfflig lösning kanske många tycker. Problemlösaren har genom skicklig
manipulation lyckats undvika att lösa ett
besvärligt ekvationssystem och snabbt bestämma parallellogrammens area. Inte mindre än 42% av de ungerska abiturienterna
löste uppgiften på detta sätt. Det finns dock
en liten hake i resonemanget. Lösningen
A = 4 är inte korrekt, vilket man ”lätt” inser på följande sätt. Om v är vinkeln mellan sidorna a och b, så är
A = ab sin v = 3 · 1 · sin v ≤ 3
Addition av (2) och (3) ger:
2x 2 + 2y2 = 10 eller x 2 + y2 = 5
Subtraktion ger som förut:
1
4xy ⋅
= 8 eller xy =
2
8
Motsvarande kurvor i xy-planet känner vi
igen. Ekvationen x2 + y2 = 5 svarar mot en
cirkel med medelpunkten i origo och radien 5 medan xy = 8 representerar
en liksidig hyperbel med koordinataxlarna som asymptoter.
Hade eleverna börjat sina undersökningar
med en överslagsberäkning borde de enligt Ambrus funnit att A högst är lika med
3 och avstått från att lägga fram resultatet
A = 4. Därmed är Ambrus färdig med sin
redogörelse för examensuppgiften och
övergår till andra frågeställningar.
Elegant men felaktig lösning
Vi kan inte gärna nöja oss med att ha fått
ta del av en möjligen elegant men felaktig
lösning. Vi måste ha svar på frågorna ”Var
ligger felet?” och ”Hur ska uppgiften lösas?”.
Vi går tillbaka till ekvationerna (1) – (3)
ännu en gång. Kontrollen ger tyvärr ingen
ledtråd. Sambanden förefaller att vara korrekta.
58
Nämnaren nr 1, 2000
För att slippa räkningar kan vi avgöra frågan om ekvationssystemet har reella eller
icke-reella lösningar genom att studera
kurvornas inbördes läge i xy-planet. Vi
observerar kurvornas symmetri med avseende på linjerna y = ± x. Det är tillräckligt
att undersöka kurvornas läge i första kvadranten. Den punkt på hyperbeln, som ligger närmast origo, är hyperbelns skärning
med linjen y = x. Punktens koordinater är
x=y=
8 ≈ 1,68
Den ligger utanför cirkeln, vars skärning
med y = x är
x=y=
5
≈ 1, 58
2
Hur ska uppgiften lösas?
Kurvorna skär inte varandra. Ekvationssystemet (2) och (3) har alltså inga reella lösningar.
Var ligger felet?
Vid det här laget måste vi fråga oss om
problemtexten innehåller motsägelser. Att
det finns oändligt många parallellogrammer med sidorna 1 och 3 längdenheter förefaller oss säkert. Kan vinkeln mellan diagonalerna i någon av dem vara 45º? Frågan är kanske inte alldeles lätt att besvara,
men vi får gräva vidare och sammanställa
ekvationerna på ett nytt sätt. Vi använder
de allmänna beteckningarna och bildar
A
kvoten 2
. Ur (1) och (4) får vi:
a − b2
A
2xy sin α 1
=
= ⋅ tan α
a2 − b 2 4xy cos α 2
Vi utnyttjar ännu en gång likheten
A = ab sin v
där v är vinkeln mellan sidorna a och b.
Insättes detta uttryck för A i likheten ovan
får vi
tan α =
2absin v
a2 − b 2
Nämnaren nr 1, 2000
Låt oss börja med att ta reda på hur stor
vinkeln är mellan sidorna a och b i vår
parallellogram. Vi sätter a = 3 och b = 1
samt α = 45º och får:
2 ⋅ 3⋅sin v
1=
vilket ger
8
4
sin v = > 1
3
Det existerar alltså ingen sådan vinkel v
och följaktligen inte heller någon parallellogram av det slag som anges i problemtexten. En icke-existerande parallellogram har
ingen area. Det förklarar de konstiga resultaten.
Vi har i det föregående ställt två frågor.
Den första frågan ”Var ligger felet” är besvarad. Problemet är orimligt för α = 45º
och kalkylerna blir meningslösa. Den andra frågan ”Hur ska uppgiften lösas?” leder till ännu en liten undersökning. Vi
måste ta reda på vilka värden α kan anta
för att uppgiften ska bli meningsfull.
Låt oss anta att v växer från 0º till 90º,
då växer sin v från 0 till 1. Och av (5) framgår att tan α växer från 0 till
2ab
2
a − b2
Om a = 3 och b = 1 så är
2 ⋅3 3
0 < tan α <
=
9 −1 4
vilket ger 0 < a < 36,8º.
För att illustrera hur uppgiften kan lösas,
väljer vi a = 3 och b = 1 och α = 30º. Eftersom
sin 30° =
1
3
och cos30° =
2
2
blir ekvationerna (1) till (4) följande:
(5)
59
Man får så småningom
1
A = 2xy ⋅
2
(1)
x 2 + y 2 + 2xy ⋅
3
=9
2
(2)
x 2 + y 2 − 2xy ⋅
3
=1
2
(3)
3
4xy ⋅
=8
2
(4) ger xy =
A=
(4)
4
och enligt (1) är
3
4
≈ 2,3 < 3
3
En kortare lösning får vi om vi använder
(5). Då blir
4
3
Avslutningsvis vill vi nämna att man ganska lätt kan finna en generell formel för
arean A. Se härledningen av (5). Av denna
framgår att
A = xy = x 1y 1 = x 2 y 2 =
a2 − b 2
A=
⋅ tan α =
2
9 −1
=
⋅ tan α = 4 tan α
2
Således gäller allmänt att
A = 4 tanα om 0 < tan α <
3
4
(a2 − b 2 ) ⋅ tan α 8⋅ tan 30°
4 Om α = 30º blir exempelvis
sin v =
=
=
2 ⋅3
3 3
2ab
4
A = 4 tan 30° =
3
och
4
4
Den enklaste och naturligaste lösningsA = absin v = 3⋅1⋅
=
3 3
3
metoden tycks dock vara den första av de
Slutligen, den som älskar att lösa ekva- ovan beskrivna metoderna. Det var den
tionssystem kan få utlopp för sin passion som 42% av Ambrus elever valde. De gjorgenom att beräkna x och y ur det system de således ganska väl ifrån sig. De misssom bildas av ekvationerna (2) och (3).
lyckades därför att problemförfattaren satte
Efter någon möda erhålls:
krokben för dem genom att ge dem en icke
existerande parallellogram att studera.
En händelse som denna kan naturligtvis
5
11
x1 = y 2 =
+
och
inte inträffa i vårt land.
2
12
5
11
y1 = x 2 =
−
2
12
där (x1,y1) och (x2,y2) är lösningarna.
60
Referenser
Ambrus, A. (1989). Indirekte Denkweisen im
Geometrieunterricht. Research Report 74, Department of Teacher Education, University of Helsinki.
Nämnaren nr 1, 2000