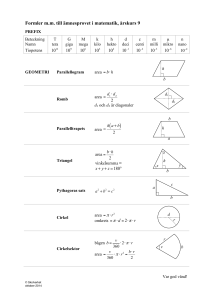
Till samtliga uppgifter krävs fullständiga lösningar

KONTROLLSKRIVNING
Kursnummer:
Moment:
Program:
Rättande lärare:
Examinator:
Datum:
Tid:
Hjälpmedel:
Omfattning och
betygsgränser:
HF0021
Matematik för basår I
KS2
Tekniskt basår
Sara Sebelius & Håkan Strömberg
Niclas Hjelm
2015-02-09
10:15-12:00
Formelsamling, miniräknare, passare,
gradskiva och linjal
För godkänd kontrollskrivning krävs 7
poäng. Godkänd kontrollskrivning innebär
att 2 poäng på ordinarie tentamen får
tillgodoräknas.
Till samtliga uppgifter krävs fullständiga
lösningar. Lösningarna skall vara tydliga
och lätta att följa.
Införda beteckningar skall definieras.
Uppställda samband skall motiveras.
Skriv helst med blyertspenna!
Lycka till!
1) Bestäm vinkeln v.
(1p)
2) Bestäm en ekvation för den räta linje som går genom punkten (1,3) och är vinkelrät mot
linjen x  2 y  2  0 .
(2p)
3) Förenkla så långt som möjligt:
(2a 2 ) 3
a)
2a 2  2a 2

1 
b)
( a  1) 2  a1 

a

4) Beräkna sträckan x i figuren.
(1p)
(2p)
(2p)
5) Anna är 1,5 m lång. Hon står 3,0 m från en lyktstolpe. Lampan sitter 4,5 m ovanför marken
(se figur). Hur lång är Annas skugga?
(2p)
6) Två koner är likformiga. Den större konens volym är 8 gånger större än den mindre konens
volym. Basarean i den mindre konen är 15 cm2. Hur stor basarea har den stora konen? 2p)
Lösningsförslag
sin v 
1)
6
6
 v  sin 1
 v  27
13
13
2) Låt den givna linjens lutning vara k1 och den sökta linjens lutning vara k 2 . För den givna
linjen gäller
x  2y  2  0
2 y  x  2
1
y   x 1
2
1
 k1  
2
Linjerna är vinkelräta. Vi får
k 1 k 2  1
k2  
1
k1
k2  
1
 (1 / 2)
k2  2
Den sökta linjen ges alltså av
y  kx  m
3  2 1  m
1 m
Svar: y  2 x  1
3a)
(2a 2 ) 3
2 3  a 23 8a 6
2


 2a 8  8
2
2
2
2
2a  2a
4a
4a
a
3b)


1 
a 
( a  1) 2  a1 
  a  2 a  1   a 
  a  2 a  1  a  a 
a
a


1 3 a
4)
tan 32 
y

10
y  10 tan 32
x y
 x  y  10 tan 47 
10
x  10 tan 47  10 tan 32  x  4,5 cm
tan 47 
5) Låt skuggans längd vara x m. Likformighet ger
x
1,5

x  3 4,5
4,5 x  1,5( x  3)
4,5 x  1,5 x  4,5
3x  4,5
4,5
3
x  1,5 m
x
Svar: Annas skugga är 1,5 m
6)
volymskala 
Vstor
 8,0
Vliten
längdskala 3  volymskala
3
 Lstor 

  8,0
 Lliten 
Lstor
 8,01 / 3  2,0
Lliten
areaskala  längdskala 2
areaskala  2,0 2  4,0
Astor
 4,0
Aliten
Astor  4,0 Aliten
Astor  4,0  15  60 cm 2
x  10 tan 47  y 
Rättningsmall
1) Rätt eller fel
2) Korrekt beräknad lutning för den sökta linjen, sedan fel
-1p
3a) Rätt eller fel

a 
3b) Förenklar till a  2 a  1   a 
 , sedan fel
a

-1p
4) ?
5) Hänvisar ej till likformighet
6) ?
-1p?