Slide 1

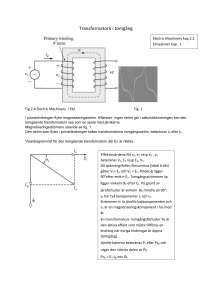
Elläradelens byggblock
Elektrostatik.
Alla laddningar har rört sig
färdigt. Inga strömmar.
Ström, motstånd, emf
Magnetism
Magnetiska krafter på laddningar
Magnetfältets källor
Elektromagnetisk induktion,
växelström
Fysiken bakom all storskalig
kraftgenerering
Elektromagnetiska vågor
Coulombs lag är en av grundbultarna.
Vi använde den för att definiera det
elektriska fältet från punktladdning.
1 q1q2
Fel 
2
4π 0 r
1
q
E
rˆ
2
40 r
F  QE
Fältlinjerna pekar i samma riktning som kraften på en liten
+ laddning. Har vi flera laddningar vektoradderas bidragen.
Tänk på en integral som en
summering av små bitar från något
som varierar kontinuerligt.
Ex. 21.10
Utsmetad laddning (linjeladdningstäthet, ytladdningstäthet,
volymsladdningstäthet): Integrera
Välj smart laddningselement. Utnyttja samband för
punktladdning!
Symmetri kan ofta utnyttjas!!
1
q
V
40 r
I ord: Elektriska
potentialen är
potentiell energi
per enhetsladdning
(Elektrisk) potential från punktladdning
(V=0 i oändligheten)
Potentialen anger en laddnings potentiella
energi enligt: U = QDV
V
V
Positiv
punktladdning
Negativ
punktladdning
Jämför uttrycken för elektriskt fält och potential från punktladdning
1
q
E
rˆ
2
40 r
1
q
V
40 r
F  qE
Vektor
U  qDV
Skalär
Relation mellan E-fält och V i en dimension
dV
E 
xˆ
dx
+
E
E, V

E = konst.
x
x
V = -Ex
Kondensator
Lägger man på en potential skiftas laddningen enligt:
Q = CV dvs. C=Q/V
Kapacitans
Med ett dielektrikum (= isolator)
istället för vakuum minskar fältet
och potentialen för en viss mängd
laddning, så C ökar.
Relation mellan strömtäthet och ström
J = I/A
Vektor!
Riktningen på
strömtätheten är
samma som på E
När vi arbetar med strömmar har vi lämnat
elektrostatiken, och då kan vi ha E-fält i ledare vilka
alstras av emf:er (ex. batterier eller generatorer)
Inne i batteriet drivs
laddningarna från
– till + (alltså mot
fältets riktning) av en
icke-elektrisk kraft.
Detta är källan till
emf.
•Ex. kemisk energi i
batteri
• El. magn. induktion
Kirchoffs lagar
Loop rule
Junction rule
Inåt räknas positivt!
Fig 25.20 BRA FIGUR!
Strömriktningarna
väljer du själv
Loopriktningarna
väljer du själv
Var konsekvent
Träna
Kraft på laddning när vi har elektriskt och magnetiskt fält
F  q( E  v  B )
Högerhandsregel för att veta riktningarna i kryssprodukt
(vektorprodukt)
F  qv  B ger alltid en kraft som är vinkelr ät mot v .
Från mekaniken vet vi att en sådan
kraft ej gör något arbete på partikeln,
men ändrar dess riktning.
Om hastigheten ligger i tavlans plan i
figuren ger mekaniken att partikeln
kommer att röra sig i en cirkel.
Även permanentmagneter kan ses som små strömslingor
kallas magnetisk dipol
Magnetisk dipol
Atom
Högerhandsregel: Fingrarna i strömmens
riktning, ytnormal och magnetiskt moment i
tummens riktning.
  IA
   B
U    B
Homogent B-fält ger bara vridmoment på magnetisk dipol
Inhomogent B-fält ger även nettokraft
Bra tabell, ger B-fält från olika sorters ledare, finns i formelblad
B-fältets källor
Högerhandsregel: Fingrarna i
strömmens riktning B-fältet i tummens
riktning
Tummen
används för
den storhet
som går
”rakt”
Högerhandsregel: Tummen i strömmens
riktning, B-fältet i fingrarnas riktning
Magnetiskt flöde ΦB
En magnet ger upphov till ett magnetiskt fält som ges av en vektor B ( x, y, z ).
Vi kallar detta ett Vektorfält . (Exakt samma resonemang kan användas om
det elektriska E fältet.)
Jämför med hastighete sfördelnin gen v ( x, y, z ) i en
strömmande vätska.
Begreppet flöde av ett vektorfält
Fig. 22.6
Induktion: Förstå fenomenet från bilden
d B
 
dt
Formell bestämning av emf riktning
från induktionslagen
1. Välj ytans riktning
2. Högerhandsregel ger
positiv emf riktning
3. Ytans riktning avgör om
flödet ökar eller minskar
4. Tillämpa induktionslagen,
tecknet ger emf riktning
Bestämma emf riktning med Lenz´s lag (Lättare)
Den inducerade strömmen vill motverka den
ursprungliga flödesändringen
Phasor-diagram. Nödvändigt för förståelsen av kap. 31!
Phasor representation av en cosinus funktion
Kommer vi även att använda när vi arbetar med växelström under nästa period.
Phasor representation av summan av två cosinus
funktioner
• Strömmen i är samma i hela kretsen
• Spänningen över R i fas med strömmen
• Spänningen över L 90o före strömmen
• Spänningen över C 90o efter strömmen
Sen är det geometri om man kan sina phasors!
Fig. 31.13
Kretsens impedans Z ges av:
Z  R  X L  X C 
2
2
1 

 R   L 

C 

2
2
V = IZ Funkar som Ohm´s lag!
Funkar både för amplituder (ovan) och rms värden
Vrms = IrmsZ
Vrms
V

2
I rms
I

2
Vid effektberäkningar i växelströmskretsar måste man
använda rms värden!
I spole och kondensator:
Pav  0
I motstånd:
Pav  Vrms I rms
I godtycklig RLC krets:
Pav  Vrms I rms cos 
Vågrörelselärans byggblock
Mekaniska vågor
Ex. vågor på sträng
Stående vågor
Ljudvågor (akustik)
Elektromagnetiska vågor
Brytningsindex, polarisation
Geometrisk optik
Strålgång i enklare optiska system
Utbredningshastighet v
Tecknet ger utbredningsriktning
=2/T
y(x,t)=Acos(kx-t+)
Amplitud A
Våglängd l
k=2/l
Periodtid T
Faskonstant, ges av begynnelse
villkoren
Frekvens f=1/T
Vinkelfrekvens 2f
Vågtal k= 2/l
k=2/l
Mediets hastighet vy
lf=v
Fig. 15.3
Fig. 15.4
Man kan representera vågen
på två sätt:
1. Välj en bestämd tid (här
t=0) och plotta y som
funktion av x.
2. Välj en bestämd punkt
(här x=0) och plotta y
som funktion av t.
Fig. 15.9
Fig. 15.10
FÖRVÄXLA EJ
DENNA
HASTIGHET
MED VÅGENS
UTBREDNINGSHASTIGHET
v = lf= /k !!!
Hastigheten vy hos en partikel i mediet, t.ex. ett kort segment av den
sträng som en våg utbreder sig med, ges av:
y ( x, t )  A cos( kx  t )
y ( x, t )
v y ( x, t ) 
 A sin( kx  t )
t
Accelerationen ay blir:
 2 y ( x, t )
2
2
a y ( x, t ) 



A
cos(
kx


t
)



y( x, t )
2
t
Stående våg
y ( x, t )  ASW (sin kx) sin  t
ASW  2 A
Observera skillnaden hos
detta uttryck och det för
en fortskridande våg. Här
är x och t separerade i
varsin funktion.
Den stående vågen
”pulserar” upp och ned,
men fortskrider ej!
Fig.
15.24
Endast vissa frekvenser!
ln=2L/n, fn=n(v/2L)
Animering av stående våg
Den stående vågen kan beskrivas som en superposition
av två motriktade fortskridande vågor.
En fortskridande våg och en stående våg beter sig helt annorlunda!
Fortskridande våg
y ( x, t )  A cos( kx  t )
Stående våg
y( x, t )  ( Asw sin( kx)) sin( t )
Interferens
Fig. 16.21
Fig. 16.22
Animeringen visar hur två harmoniska vågor med en liten
frekvensskillnad alstrar en beat-frekvens.
Stående vågor i orgelpipor
Fig. 16.16
Fig. 16.17
Båda ändar öppna
”open pipe”
Fig 16.18
En ända stängd
”stopped pipe”
Dopplereffekten
v är ljudhastigheten
vL är lyssnarens
hastighet
vS är källans
(source) hastighet
Fig. 16.26
OBS vL och vS mäts
relativt luftmassan
v  vL
fL 
fS
v  vS
Positiv riktning är
Fig. 16.27
från L mot S
Kap. 33. Härifrån arbetar vi
med elektromagnetiska vågor,
framför allt ljus.
Brytningsindex n = c/v
är nu en viktig storhet.
Vinklarna mäts mot ytnormalen.
Reflektionslagen: qa = qr
Refraktionslagen: nasin qa = nbsin qb
(Snells lag)
Sambanden för
reflektion och
brytning är enkla:
Alla strålar ligger i planet som definieras av den
infallande strålen och ytnormalen, infallsplanet.
nb > na ger brytning mot normalen
nb < na ger brytning från normalen
Detta fall kan leda till
totalreflektion!
Vinkelrätt infall ger ingen brytning
Fig. 33.8
Här hamnar bilden bakom
spegeln där det inte finns
något ljus. Bilden hamnar
där strålarnas förlängning
skär varandra. Detta är
exempel på en virtuell bild.
Här alstras bilden där
verkliga ljusstrålar skär
varandra. Vi har en reell
bild.
Lär er att rita diagram med ”principal rays”
både för linser och speglar!
Det räcker med två
principal rays för att
konstruera bilden.
Formeln för
bildalstring i
sfäriska speglar
och tunna linser
är densamma:
1/s +1/s´=1/f
Viktigt att ha
koll på
teckenreglerna
som står i
formelhäftet!
Förstoringsglaset
tan q~ q =y/25 cm
tan q´~ q´ =y/f
M=q´/q = (y/f)/(y/25 cm)=25 cm/f
Fig. 34.51
Observera att detta är vinkelförstoring.