Problem

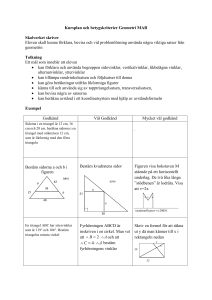
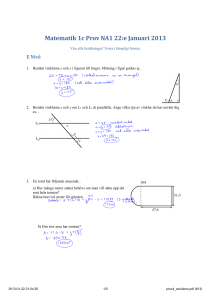
Lektion 12. Mattedrabbning om vinklar
1. AB är en diameter i en cirkel, punkten C ligger på cirkelns periferi. Bestäm ACB.
2. ABC är en triangel, BD – en bisektris. Man vet att AB=BD=DC. Bestäm vinklarna i triangeln
ABC.
3. ABC är en likbent triangel, AB=BC, B=70. Bisektrisen CD och höjden AH skär varandra i
en punkt K. Bestäm AKC.
4. O är en sådan punkt utanför kvadraten ABCD att OAB är en liksidig triangel. Bestäm COD.
5. ABC är en triangel, BD – en median. Man vet att ABD är en liksidig triangel. Bestäm vinklarna
i triangeln ABC.
6. ABC är en triangel. A=40 , O är mittpunktnormalernas skärningspunkt. Bestäm BOC.
Den 18 oktober, Metapontum, åk2 http://sasja.shap.homedns.org/Metapontum/2006/ht2/
Lektion 12. Mattedrabbning om vinklar
1. AB är en diameter i en cirkel, punkten C ligger på cirkelns periferi. Bestäm ACB.
2. ABC är en triangel, BD – en bisektris. Man vet att AB=BD=DC. Bestäm vinklarna i triangeln
ABC.
3. ABC är en likbent triangel, AB=BC, B=70. Bisektrisen CD och höjden AH skär varandra i
en punkt K. Bestäm AKC.
4. O är en sådan punkt utanför kvadraten ABCD att OAB är en liksidig triangel. Bestäm COD.
5. ABC är en triangel, BD – en median. Man vet att ABD är en liksidig triangel. Bestäm vinklarna
i triangeln ABC.
6. ABC är en triangel. A=40 , O är mittpunktnormalernas skärningspunkt. Bestäm BOC.
Den 18 oktober, Metapontum, åk2 http://sasja.shap.homedns.org/Metapontum/2006/ht2/
Lektion 12. Mattedrabbning om vinklar
1. AB är en diameter i en cirkel, punkten C ligger på cirkelns periferi. Bestäm ACB.
2. ABC är en triangel, BD – en bisektris. Man vet att AB=BD=DC. Bestäm vinklarna i triangeln
ABC.
3. ABC är en likbent triangel, AB=BC, B=70. Bisektrisen CD och höjden AH skär varandra i
en punkt K. Bestäm AKC.
4. O är en sådan punkt utanför kvadraten ABCD att OAB är en liksidig triangel. Bestäm COD.
5. ABC är en triangel, BD – en median. Man vet att ABD är en liksidig triangel. Bestäm vinklarna
i triangeln ABC.
6. ABC är en triangel. A=40 , O är mittpunktnormalernas skärningspunkt. Bestäm BOC.
Den 18 oktober, Metapontum, åk2 http://sasja.shap.homedns.org/Metapontum/2006/ht2/