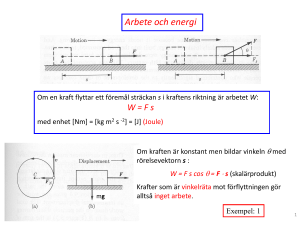
Elektromagnetisk strålning
Maxwell:
Ljus: Elektromagnetisk våg
(Experiment av Heinrich Hertz)
Oscillerande elektrisk ström i tråd ger oscillerande
elektriska och magnetiska fält med samma frekvens.
Detta EM fält har samma egenskaper som ljus: reflektion,
refraktion, interferens, polarisation, hastighet (c)
5A1247, modern fysik, VT2007, KTH
Fotoelektriska effekten
(Hertz, Thomson, Lenards)
Ljus slår ut elektroner från metallplattan.
Maximal kinetisk energi för elektronerna mäts genom att bromsa
upp dem med negativ spänning på kollektorn.
Ekin,max = qeV
Klassiskt: maximal kinetisk energi borde bero av ljusintensiteten.
Experimentellt:
Ekin,max beror inte av intensitetet men däremot av ljusets frekvens
5A1247, modern fysik, VT2007, KTH
Einstein (1905): Ljuset uppträder som partikel, foton, med energi hf
E = hf
Ekin,max = hf – φ
där φ är utträdesarbetet
5A1247, modern fysik, VT2007, KTH
Comptonspridning
Compton et al visade 1922 att röntgenljusets spridning mot
”fria” elektroner inte kunde förklaras med klassisk vågmekanik
utan krävde att vi behandlade ljuset som partiklar och räknade
relativistiskt.
Våglängdsskillnaden i inkommande och spritt ljus beror inte av
intensiteten utan bara av spridningvinkeln.
Låt inkommande foton ha rörelsemängd p .
Spridd foton har rörelsemängd p´.
Vinklar θ,φ ur figuren.
Rörelsemängden bevaras.
⊥:
p ´sinθ = pe sin φ
||: p = p ´cos θ + pe cos φ
Eliminera φ :
(
)
pe 2 cos2 φ + sin2 φ = p 2 + p ´2 cos2 θ − 2pp ´cosθ + p ´2 sin2 θ
pe 2 = p 2 + p ´2 −2pp ´cosθ
2
2 2
2 4
ger uttryck för pe2
Ee = pc − p ´c + me c 2 men vi har även: Ee = pe c + me c
2
= pc − p ´c + me c 2 − me 2c 4 = p 2c 2 + p ´2c 2 − 2 pp ´c 2 + 2me c 3 ( p − p ´)
(2)
Även energin bevaras ⇒
pe 2c 2 = Ee 2 − me 2c 4
Kombinera (1) och (2):
Med p =h/λ fås:
(1)
(
)
2 pp ´(1 − cos θ ) = 2me c (p − p ´)
h2
(1 − cos θ ) = hme c ⎛⎜ 1 − 1 ⎞⎟
λλ´
⎝ λ λ´⎠
⇒
λ'−λ =
h
(1 − cos θ )
me c
5A1247, modern fysik, VT2007, KTH
Comptonspridning (forts)
Den härledda formeln stämmer väl överens med data!!
Notera att elektronen tillförs maximal kinetisk energi då θ = -π.
För fotonenergier Eγ >> mec2 kan man visa att elektronens kinetiska
energi är:
Eekin≈Eγ – ½ (mec2)
5A1247, modern fysik, VT2007, KTH
