Längd: En meter (m) är den sträcka som ljuset tillryggarlägger i

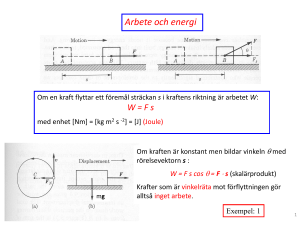
Potentiellenergi, kinetisk energi och arbete, kapitel 7-8
Arbete
Om en kraft flyttar ett föremål sträckan s i kraftens riktning är arbetet W:
W  Fs
Om kraften är konstant men bildar vinkeln  med rörelsevektorn s :
W  Fs cos   F s (Skalärprodukt)
Krafter vinkelräta mot förflyttningen för alltså inget arbete, se nedan.
Abete som tillförs ett objekt är positivt och arbete som tas ifrån objektet är negativt.
Föreläsning 5
Kp 7-8, TFYY97 Mekanik för KB 2006
Föreläsare: Urban Forsberg
Arbete vid rörelse längs en bana
Arbete när partikeln rör sig sträckan A till B, dr (vektor) så gäller
dW  F dr
där
F  Fx xˆ  Fy yˆ  Fz zˆ och dr  dxxˆ  dyyˆ  dzzˆ
Vidare vet vi att ds  dr , detta ger att dW  F dr  Fds cos 
Vi vet också att FT  F cos vilket ger att dW  FT ds , där index T avser på den tangentiellt
riktade kraften.
W  F1 dr1  F2 dr2  F3 dr3  F4 dr4  ...   Fi dri
i
Vilket kan skrivas som
B
B
A
A
W   Fdr   FT ds
Föreläsning 5
Kp 7-8, TFYY97 Mekanik för KB 2006
Föreläsare: Urban Forsberg
Kinetisk energi (rörelseenergi)
Kinetisk energi är relaterad till ett objekts rörelse. Högre hastighet resulterar i högre kinetisk
energi och motsatt, om objektet står stilla så är den kinetiska energin noll.
Betrakta arbetet när en partikel rör sig sträckan ds längs en godtycklig kurva. Arbetet dW
ges som vi vet av
dW  FT ds
N II lag ger: FT  ma  m
dv
dt
Kombinera dessa två ekvationer ger
dW  m
dv
ds
ds  m dv  mvdv
dt
dt
Genom att integrera denna ekvation från position A till position B så erhåller vi:
B
B
A
A
W   dW   mvdv 
1 2 1 2
mvB  mv A
2
2
Det arbete som kraften F har gjort på partikeln under sträckan A till B är alltså skillnaden i
2
kinetisk energi. Vi kallar mv
för partikelns kinetiska energi Ek. Man kan också skriva om
2
mv 2
p2
  p  mv  
detta som Ek 
, där p är rörelsemängdsmomentet (kommer senare).
2
2m
Arbetet en kraft gör på en partikel är lika med förändringen i kinetisk energi, GÄLLER
ALLTID.
Föreläsning 5
Kp 7-8, TFYY97 Mekanik för KB 2006
Föreläsare: Urban Forsberg
Arbete som utförs av gravitationskraften
Det arbete som gravitationskraften utförs skrivs som
Wg  Fg cos   d  mgd cos 
Då   00 är Wg  mgd och arbetet som utförs är positivt. Sammanfattningsvis så utförs ett
positivt arbete då objektet förflyttas mot jordens centrum och ett negativt arbete då kroppen
förflyttas ifrån jorden centrum.
Arbete – Kinetisk Energi
Låt K vara förändringen av kinetisk energi, låt W vara netto arbetet som utförs på systemet.
Då gäller
K  K f  Ki  W
Där Kf och Ki är den kinetiska energin efter (f=final) och före (i=initial) förändringen.
Fjädrar och dess arbete
Fex
i
A
B
l0
l
x
För att kunna stäcka ut en fjäder med längden l0, som befinner sig i vila, till längden l behöver
man tillföra en kraft Fex  k (l  l0 ) xˆ , där k kallas för fjäderkonstant [N/m]. Den kraft som
fjädern verkar på m och är motriktad Fex kallas för fjäderkraften och beskrivs av
Ff  k (l  l0 ) xˆ  kxxˆ
Denna ekvation kallas för Hooke’s lag. Observera att kraften är negativ då vi drar ut fjädern
och positiv då vid trycker ihop den, med ovanstående val av riktning på axeln x.
Vad är då arbetet som uträttas av fjädern då man drar ut den från l0 till l ?
Föreläsning 5
Kp 7-8, TFYY97 Mekanik för KB 2006
Föreläsare: Urban Forsberg
l
l
l
k
W fjäder  dW   Fdx   kxdx  k  xdx   ( xl2  xl20 )
2
l0
l0
l0
Om l=0 så gäller att W fjäder  
k 2
xl
2 0
Effekt
Om arbetet som uträttas under tiden t är medeleffekten Pmedel 
Momentaneffekt P 
W
t
dW
dt
Man kan också skriva P 
dW F cos dx
 dx 

 F cos     Fv cos  vilket kan skrivas
dt
dt
 dt 
som
PF v
Sorter för arbete (energi) och effekt
W [J] Joule [kgm2s-2]
P [W] Watt [J/s]
Andra vanliga energier (dock ej SI enheter) är
kcal (kilokalorier) Energi som krävs för att öka temperaturen hos 1 kg vatten från 14.5 grader
till 15.5 grader vid 1 atm (4186,8J)
1 hk (hästkraft) Den effekt som krävs för att lyfta 75 kg 1 m på 1 s (736 W).
Föreläsning 5
Kp 7-8, TFYY97 Mekanik för KB 2006
Föreläsare: Urban Forsberg